Машинная арифметика и относительные единицы

1.

Машинная арифметика и
относительные единицы
• Знакомство с различными подходами к математическим
вычислениям – в целочисленном формате с
фиксированной точкой и в формате с плавающей точкой.
• Синтез фильтра (инерционного звена первого порядка) в
цифровом виде, реализация его при помощи различных
подходов.

2.

Проблемы двоичных вычислений
0
0
0
1
0
0
1
*
0
0
0
0
Аккумулятор 0
0
0
0
0
0
Память
0
0
0
0
0
0
0
0
0
0
?
1
0
1
0
0
0
1
0
1
0
0
0
0
0
0
1
0
0
0
0
0
4
* 3
1 2
Допустим, что исходные данные
представляют собой 4-разрядные целые
числа со знаком. Диапазон их
возможного изменения от -8 до +7. При
умножении результат умещается в 8
разрядах.
Сохранить результат без потери
знаков можно в две 4-разрядные ячейки
памяти.
Сохранять только младшую часть
нельзя, так как она может не вместить
весь результат умножения.
Уже в данном конкретном примере
ответ равен 12, что выходит из
диапазона
допустимых
значений
знаковых 4-разрядных чисел, и, будучи
сохраненной, младшая часть результата
будет в дальнейших вычислениях
восприниматься числом
-4, что
совершенно недопустимо.

3.

Проблемы двоичных вычислений
Решение 1: увеличение разрядности данных
Решение 2: использование относительных
единиц и целочисленного формата с
фиксированной точкой
Решение 3: использование формата
плавающей точки

4.

Числа с плавающей точкой
Числа с плавающей точкой представляются в современных микроконтроллерах в 32разрядном виде, соответствующем стандарту IEEE Std. 754 Single Precision FloatingPoint. Типы double и long double пока не поддерживаются ни одним из существующих
микроконтроллеров семейства Motor Control.
31 30
23 22
0
s e e e e e e e e f f f f f f f f f f f f f f f f f f f f f f f
1 знаковый разряд
8-разрядная экспонента
23-разрядная мантисса
e 255 and f 0 then v NaN ;
if e 255 and f 0 then v 1 ;
if
s
s
if 0 e 255 then v 1 2e 127 1. f ;
if
e 0 and f 0 then v 1 2
if
e 0 and f 0 then v 1 0.
s
1,920929 10 38
e 126
0. f ;
s
3, 4028235 1038

5.

Проблемы вычислений с числами с плавающей точкой
(очень большие и очень малые числа)
Преобразование частоты в угол и синус и косинус угла
f
t
2
0
1
p
SIN
COS
sin
cos

6.

Относительные единицы
Для расчета математических моделей, описания алгоритмов системы управления,
измерений электрических и механических величин и цифровой фильтрации удобно
использовать системы относительных единиц. Относительные единицы получаются
путем деления реальной физической величины на некоторое базовое значение. Базовые
значения можно выбирать по-разному, однако чаще всего за базовое число принимают
номинальное значение физической величины.
0
0
0
0
Аккумулятор 0
0
0
0
0
0
0
0
0
0
0
0
* 0
0 0
0 1
0 0
0 0
0,1
1,0
0,1
1 0
0 1
0 0
0 0
1 1
Память 0 0 , 1 1
1
1
1
0
0
0
1
1,25
* 0,75
0,9375
0,75
0
0
0
0
Z
0
0
0
Y
Z
0
0
Y
Y
Z
X
* X
0 E
Y Y
Y Y
Y E
Z, R
X, X
X, X
E E
Y E
E 0
0 0
E E
E
E
E
0
0
0
E
Z Z, R E
Пусть ток будет равен 1,25 номинала, а напряжение
0,75 от номинального значения (базовое значение в данном
случае равно номинальному). Выберем формат для
представления тока и напряжения, где 2 разряда будет
отведено на целую часть и два — на дробную.

7.

Относительные единицы
К преимуществам относительных единиц следует отнести:
определенность с разрядностью всех вычислений в системе;
независимость представления данных системы управления и
моделей от номинальной мощности, номинальной скорости,
номинального тока и других параметров, которые могут
меняться от объекта к объекту;
в относительных числах можно избежать использования
иррациональных чисел и производить операции, не накапливая
погрешности;
удобно задавать настройки и ограничения работы системы
управления в процентах от номинала, которые могут
редактироваться и отображаться на интерфейсных устройствах в
абсолютных единицах (СИ) независимо от мощности
электропривода.

8.

Числа с фиксированной точкой и библиотека IQmath
31 30
24 23
0
s i i i i i i i f f f f f f f f f f f f f f f f f f f f f f f f
1 знаковый разряд
7 разрядов целой части
24 разряда дробной части
Формат IQ 8.24:
24 разряда дробной части обеспечивают 2^24=16777216
градаций дробной части, что более чем достаточно для
реальных задач электропривода
7 разрядов целой части обеспечивают запас
перегрузочной способности в диапазоне +127 и -128.
При верном выборе базовых величин относительных
единиц переполнение не произойдет ни в каком случае:
есть большой запас

9.

Выбор системы относительных единиц
Следует выбрать непротиворечивую систему базовых величин
x
x
,
Xб
*

10.

Выбор системы относительных единиц
Следует выбрать непротиворечивую систему базовых величин
x
x
,
Xб
*
Пример выбора базовых величин
Основные:
U б U я ном
I б I я ном
б 0
U я ном
k ном

11.

Выбор системы относительных единиц
Следует выбрать непротиворечивую систему базовых величин
x
x
,
Xб
*
Пример выбора базовых величин
Основные:
Производные:
U б U я ном
Pб U б I б
I б I я ном
Mб
б 0
U я ном
k ном
Pб
б
U
Rб б
Iб
Rб
б
U
k б б
б
Lб

12.

Перевод уравнений в ОЕ
U я ном 110 В;
I я ном 10 А;
Rя 1 Ом;
В×с
k ном 1
;
рад
рад
ном 100
;
с
Lя 0, 010 Гн.
U DC 110 В;
1
TШИМ
с;
10000
uвых U DC .

13.

Перевод уравнений привода в ОЕ
U я ном 110 В;
I я ном 10 А;
Rя 1 Ом;
В×с
k ном 1
;
рад
рад
ном 100
;
с
Lя 0, 010 Гн.
U DC 110 В;
1
TШИМ
с;
10000
uвых U DC .
d iя
u
k
i
R
L
ном
я я
я
я
d
t
M k номiя
Mб
.
Uб
;
uя k ном iя Rя
d iя
1
Lя
;
U б k б б I б Rб Lб б I б
dt
k номiя
M
,
Mб
k б Iб
*
d
i
*
*
*
* *
*
я
uя k ном iя Rя Lя * ;
dt
M * k *ном iя* ,

14.

Перевод уравнений привода в ОЕ
Основные:
U б U я ном 110 В;
I б I я ном 10 А;
б 0
U я ном
k ном
110
рад
.
с
Производные:
Pб U б I б 110 10 1100 Вт;
Mб
Pб 1100
10 Н×м;
б 110
Rб
U б 110
11 Ом;
Iб
10
Lб
Rб
11
0,1 Гн;
б 110
k б
U б 110
В×с
1
.
б 110
рад

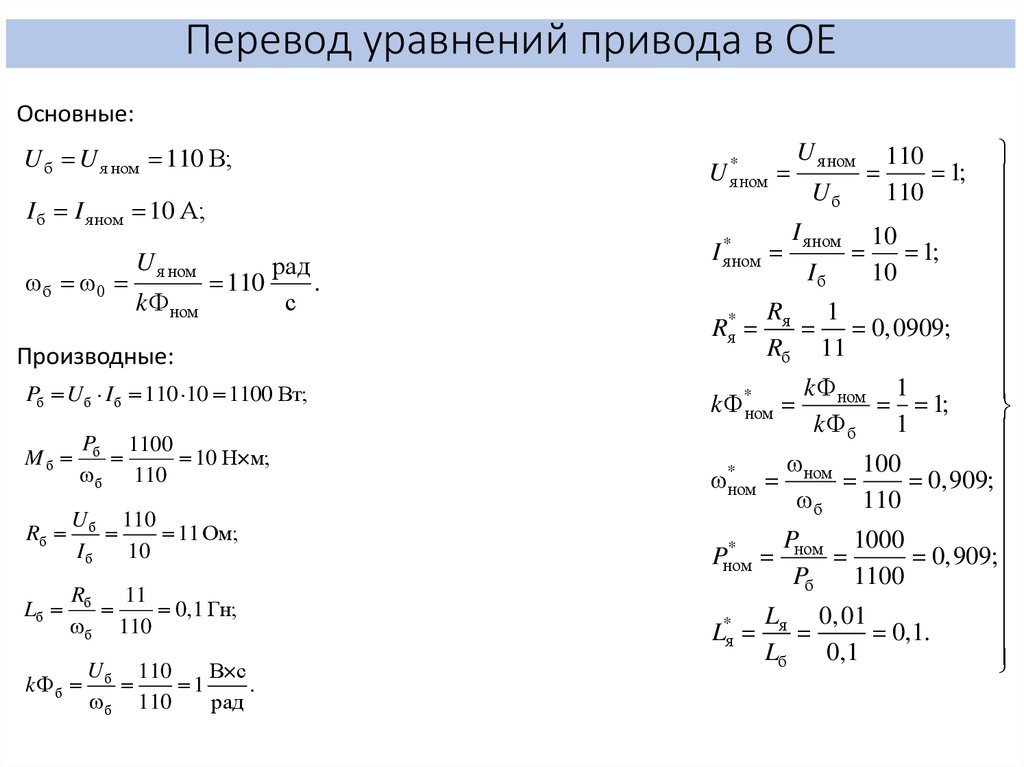
15.

Перевод уравнений привода в ОЕ
Основные:
U б U я ном 110 В;
I б I я ном 10 А;
б 0
U я ном
k ном
110
рад
.
с
Производные:
Pб U б I б 110 10 1100 Вт;
Mб
Pб 1100
10 Н×м;
б 110
Rб
U б 110
11 Ом;
Iб
10
Lб
Rб
11
0,1 Гн;
б 110
k б
U б 110
В×с
1
.
б 110
рад
Uб
I я ном 10
*
I я ном
1;
Iб
10
Rя 1
*
Rя
0, 0909;
Rб 11
k ном 1
*
k ном
1;
k б
1
ном 100
*
ном
0,909;
б
110
Pном 1000
*
Pном
0,909;
Pб
1100
Lя 0, 01
*
Lя
0,1.
Lб
0,1
U я*ном
U я ном
110
1;
110

16.

Целочисленные вычисления
Плавающая точка
Да
Нет
Проблемы при
использовании очень
больших чисел
Да, ест риск переполнения
Да, есть риск неверных
вычислений при наличии
в выражении малых чисел
Проблемы при
использовании очень
маленьких чисел
Да, ест риск потери
точности
Да, есть риск неверных
вычислений при наличии
в выражении больших
чисел
Скорость вычислений
Выше благодаря
вычислительным трюкам
типа замены деления
сдвигом
Ниже, требуется
аппаратная поддержка
плавающей точки
Проблемы при компиляции
Нет, всегда вычисляется
корректно
Риск неоптимального
использованием
аппаратного ускорителя
Переносимость кода
Хорошая, целочисленные
вычисления
поддерживаются на всех
Плохая, если нет или
слабый FPU в целевом
устройстве
Необходимость
использования
относительных единиц

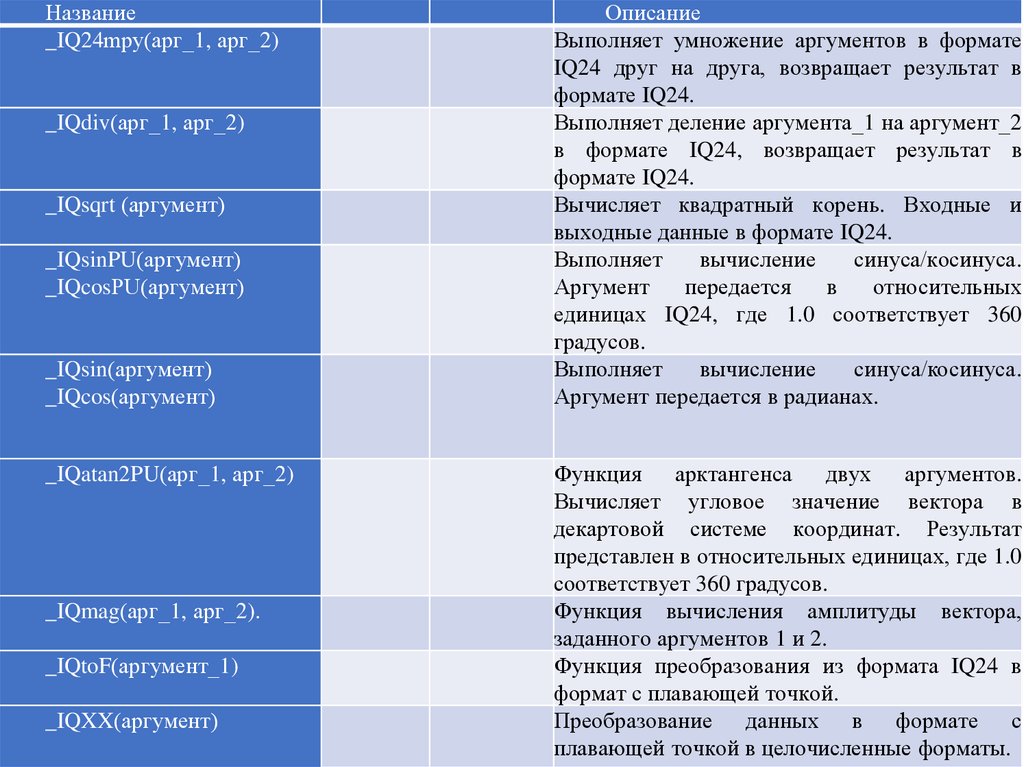
17.

Название
_IQ24mpy(арг_1, арг_2)
_IQdiv(арг_1, арг_2)
_IQsqrt (аргумент)
_IQsinPU(аргумент)
_IQcosPU(аргумент)
_IQsin(аргумент)
_IQcos(аргумент)
_IQatan2PU(арг_1, арг_2)
_IQmag(арг_1, арг_2).
_IQtoF(аргумент_1)
_IQXX(аргумент)
Описание
Выполняет умножение аргументов в формате
IQ24 друг на друга, возвращает результат в
формате IQ24.
Выполняет деление аргумента_1 на аргумент_2
в формате IQ24, возвращает результат в
формате IQ24.
Вычисляет квадратный корень. Входные и
выходные данные в формате IQ24.
Выполняет
вычисление
синуса/косинуса.
Аргумент
передается
в
относительных
единицах IQ24, где 1.0 соответствует 360
градусов.
Выполняет
вычисление
синуса/косинуса.
Аргумент передается в радианах.
Функция арктангенса двух аргументов.
Вычисляет угловое значение вектора в
декартовой системе координат. Результат
представлен в относительных единицах, где 1.0
соответствует 360 градусов.
Функция вычисления амплитуды вектора,
заданного аргументов 1 и 2.
Функция преобразования из формата IQ24 в
формат с плавающей точкой.
Преобразование данных в формате с
17
плавающей точкой в целочисленные форматы.