Уравнение окружности и прямой

1. Уравнения прямой и окружности

2.

Уравнение линии на плоскости
y
y=x
L
M(x;y)
O
x
D(x;y)
C(x;y)
- Если точка лежит на данной линии, то ее координаты
удовлетворяют уравнению этой линии.
- Координаты любой точки, не лежащей на данной линии, не
удовлетворяют ее уравнению.
2

3. При изучении линий методом координат возникают 2 задачи:

• По геометрическим свойствам данной
линии найти её уравнение;
• Обратная задача: по заданному уравнению
линии исследовать её геометрические
свойства.
3

4.

Повторение:
1. Дайте определение окружности.
2.Какими параметрами можно задать
окружность единственным образом ?
3. Что такое центр и радиус окружности?
4. Как называется отрезок, соединяющий две
точки окружности ?
5. Как называется хорда проходящая через
центр окружности ?
4

5. Уравнение окружности

5

6.

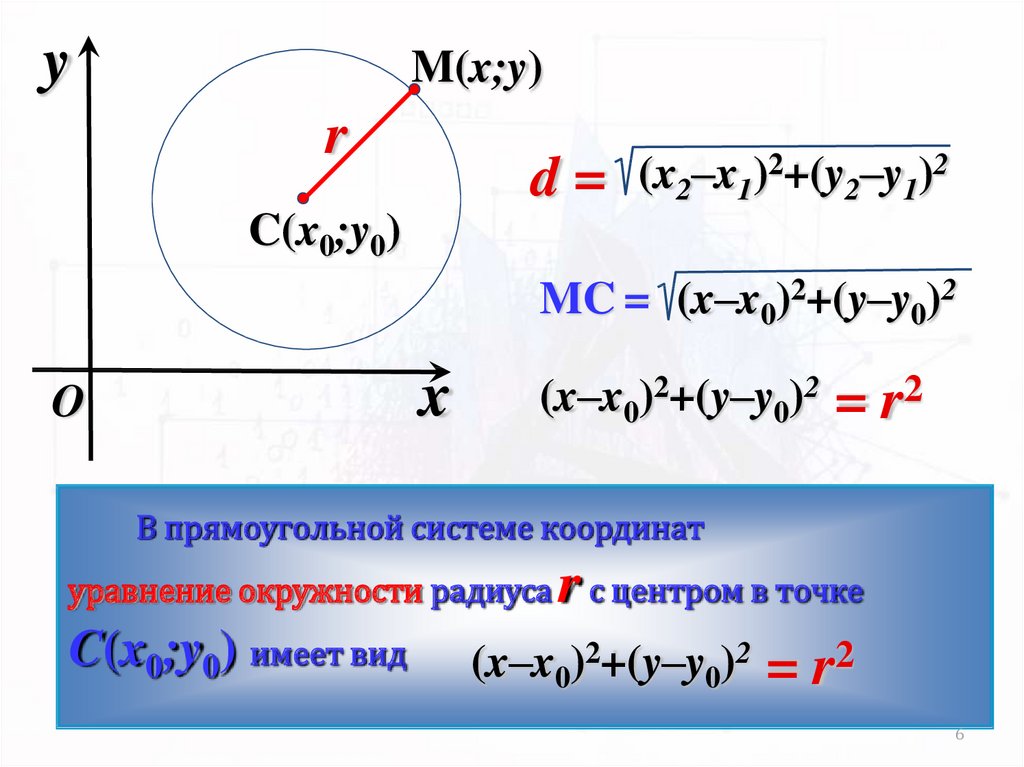
y
M(x;y)
r
d=
(x2–x1)2+(y2–y1)2
C(x0;y0)
MC = (x–x0)2+(y–y0)2
x
O
(x–x0)2+(y–y0)2
= r2
В прямоугольной системе координат
r с центром в точке
(x–x0)2+(y–y0)2 = r2
уравнение окружности радиуса
C(x0;y0) имеет вид
6

7.

y
O
r =3
r
(x – x0)2 + (y – (y20))2 = 9r 2
x
C(4;-2)
4 -2
В прямоугольной системе координат
r с центром в точке
(x–x0)2+(y–y0)2 = r2
уравнение окружности радиуса
C(x0;y0) имеет вид
7

8.

y
x0
y0
(x –( -3
3 ))2 + (y – (-2
2 ))2 = 9
32
O
r
x
C( x0; y0)
r=3
C(-3;-2)
В прямоугольной системе координат
r с центром в точке
(x–x0)2+(y–y0)2 = r2
уравнение окружности радиуса
C(x0;y0) имеет вид
8

9.

Уравнение окружности
Центр
r
(x – 3 )2 + (y – 2)2 = 16
(x – 1 )2 + (y + 2)2 = 4
(x + 5 )2 + (y – 3)2 = 25
(x – 1 )2 + y 2 = 8
x 2 + (y + 2)2 = 2
x 2+ y 2= 9
(x – 3 )2 + (y – 2)2 = 0,09
(x + 7)2 + (y – 5)2 = 2,5
C(3; 2)
r=4
C(1;-2)
r=2
C(-5; 3)
C(1; 0)
r=5
r= 8
C(0;-2)
C(0; 0)
r= 2
r=3
C(3; 2)
C(-7; 5)
r = 0,3
r = 2,5
5
r= 2
x2 +
(y +
4)2 =
1
64
C(0;-4)
9

10.

Уравнение окружности
Центр
r
(x – 1 )2 + (y – 2)2 = 64
(x – 1 )2 + (y + 2)2 = 0,64
(x + 5 )2 + y 2 = 1,44
x 2+ y 2= 5
(x + 6)2 + (y + 2)2 = 7
(x – 5)2 + y 2 = 0,0169
(x – 3 )2 + (y + 2)2 = 0,09
(x + 7)2 + (y – 5)2 = 1,6
C(1; 2)
r=8
C(1;-2)
r = 0,8
C(-5; 0)
C(0; 0)
r = 1,2
r= 5
C(-6;-2)
C(5; 0)
r= 7
r = 0,13
C(3; -2)
C(-7; 5)
r = 0,3
r = 1,6
1
r = 13
x2 +
(y +
16
2
4) = 9
C(0;-4)
10

11.

Уравнение окружности
Центр
r
(x – 3 )2 + (y – 2)2 = 16
(x – 1 )2 + (y + 2)2 = 4
(x + 5 )2 + (y – 3)2 = 25
(x – 1 )2 + y 2 = 8
x 2 + (y + 2)2 = 2
x 2+ y 2= 9
(x – 3 )2 + (y – 2)2 = 0,09
(x + 7)2 + (y – 5)2 = 2,5
C(3; 2)
r=4
C(1;-2)
r=2
C(-5; 3)
C(1; 0)
r=5
r= 8
C(0;-2)
C(0; 0)
r= 2
r=3
C(3; 2)
C(-7; 5)
r = 0,3
r = 2,5
5
r= 2
x2 +
(y +
4)2 =
1
64
C(0;-4)
11

12.

Уравнение окружности
Центр
r
(x – 1 )2 + (y – 2)2 = 64
(x – 1 )2 + (y + 2)2 = 0,64
(x + 5 )2 + y 2 = 1,44
x 2+ y 2= 5
(x + 6)2 + (y + 2)2 = 7
(x – 5)2 + y 2 = 0,0169
(x – 3 )2 + (y + 2)2 = 0,09
(x + 7)2 + (y – 5)2 = 1,6
C(1; 2)
r=8
C(1;-2)
r = 0,8
C(-5; 0)
C(0; 0)
r = 1,2
r= 5
C(-6;-2)
C(5; 0)
r= 7
r = 0,13
C(3; -2)
C(-7; 5)
r = 0,3
r = 1,6
1
r = 13
x2 +
(y +
16
2
4) = 9
C(0;-4)
12

13.

№ 960 (a) Какие из точек лежат на окружности?
x 2 + y 2 = 25
Центр?
O(0; 0)
A(3; -4);
32 + (-4)2 = 25
B(1; 0);
12 + 0 2 <
= 25
C(0; 5);
Радиус?
r=5
Верно
y
C
02 + 5 2 = 25 Верно
E
2+
2
D(0; 0);
0
E(0; 1);
0 2+ 1 2 =
< 25
0 <
= 25
5
D B
A
13
x

14.

№ 960 (б) Какие из точек лежат на окружности?
Центр?
2
2
(x
x – 1) + (yy + 3) = 9
A(3; -4);
O(1;-3)
Радиус? r = 3
(3 – 1)2 + (– 4 + 3)2 =
<9
B(1; 0);
(1 – 1)2 + (0 + 3)2 = 9
C(0; 5);
(0 – 1)2 + (5 + 3)2 >
=9
D(0; 0);
(0 – 1)2 + (0 + 3)2 >
=9
E(0; 1);
(0 – 1)2 + (1 + 3)2 >
=9
Верно
14

15.

y + 3)2 = 100
(xx – 4 )2 + (y
Дана окружность
Определите, какие из точек А(-4; 3), В(5; 1), С(-5; 4), D(10; 5)
лежат: а) на окружности;
б) внутри круга, ограниченного данной окружностью;
в) вне круга, ограниченного данной окружностью.
(– 4 – 4)2 + (3 + 3)2 > 100
(5 – 4)2 + (1 + 3)2 < 100
(– 5 – 4)2 + (4 + 3)2 > 100
(10 – 4)2 + (5 + 3)2 = 100
15

16. Домашнее задание

Формулы
№№ 959( в нём найти только центр и
радиус), 960(б), 963, 966, 967
Благодарю за внимание
16

17. Уравнение прямой

17

18.

Уравнения прямых
Прямые
на координатной
плоскости могут
располагаться только
тремя способами:
• горизонтально
• вертикально
• под наклоном к
осям
18

19.

Уравнение вертикальных прямых
Уравнение вида x = a
на координатной плоскости задает множество
точек, имеющих одну и ту же абсциссу.
Рассмотрим, например, уравнение:
x=1
Отметим на координатной плоскости
некоторые точки, имеющие абсциссу, равную
1.
19

20.

Уравнение вертикальных прямых
Эти точки лежат на
вертикальной прямой,
проходящей через
точку с абсциссой 1 на
оси ОХ.
х=1
Например:
(1; 0), (1;2), (1; -2).
Это значит, что уравнение x
= a задает на плоскости
вертикальную прямую.
20

21.

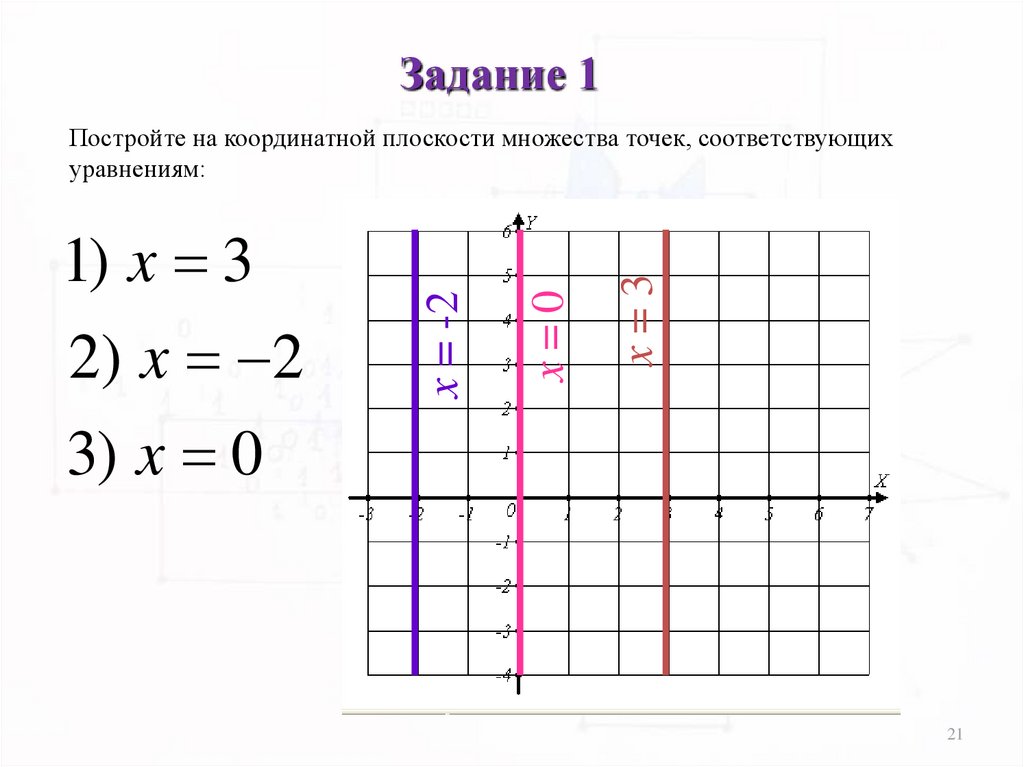
Задание 1
x=3
2) x 2
3) x 0
x=0
1) x 3
x = -2
Постройте на координатной плоскости множества точек, соответствующих
уравнениям:
21

22.

Уравнение горизонтальных прямых
Уравнение вида y = b
на координатной плоскости задает множество
точек, имеющих одну и ту же ординату.
Рассмотрим, например, уравнение:
y=1
Отметим на координатной плоскости
некоторые точки, имеющие ординату,
равную 1.
22

23.

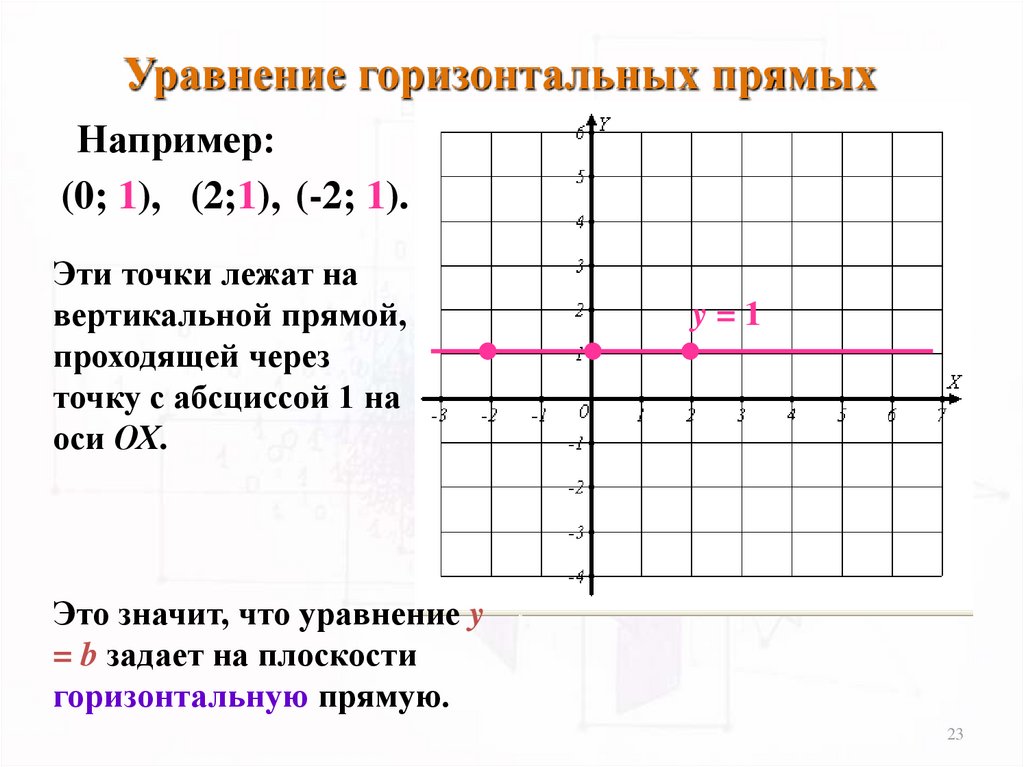
Уравнение горизонтальных прямых
Например:
(0; 1), (2;1), (-2; 1).
Эти точки лежат на
вертикальной прямой,
проходящей через
точку с абсциссой 1 на
оси ОХ.
y=1
Это значит, что уравнение y
= b задает на плоскости
горизонтальную прямую.
23

24.

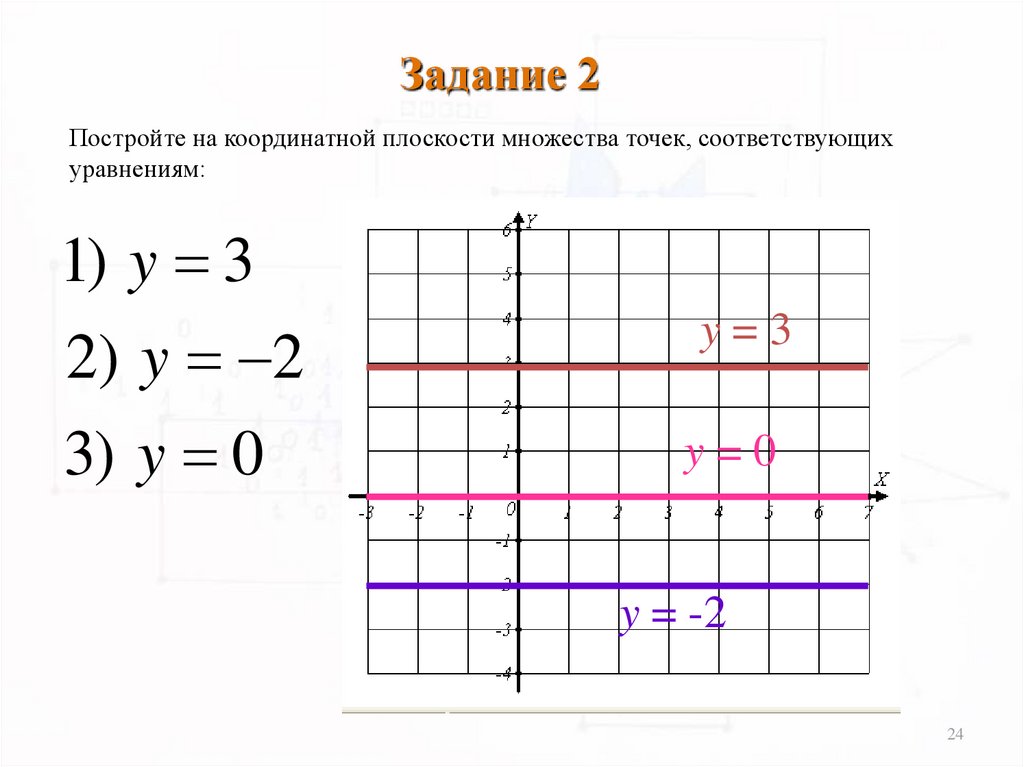
Задание 2
Постройте на координатной плоскости множества точек, соответствующих
уравнениям:
1) y 3
2 ) y 2
3) y 0
y=3
y=0
y = -2
24

25.

Каноническое уравнение прямых
Мы привыкли к тому, что на координатной плоскости
прямая – это график линейной функции, которая задана
уравнением вида:
y kx b
Рассмотрим следующее уравнение прямой:
Каноническая
запись
2
1
y x
3
2
6 y 4 x 3
4x 6 y 3 0
25

26.

Каноническое уравнение прямых
В общем виде:
Ax By C 0
В канонической записи уравнения прямых принято
использовать целые коэффициенты.
Выполним обратную операцию:
By Ax C
A
C
y x
B
B
То есть:
A
k
B
C
b
B
26

27.

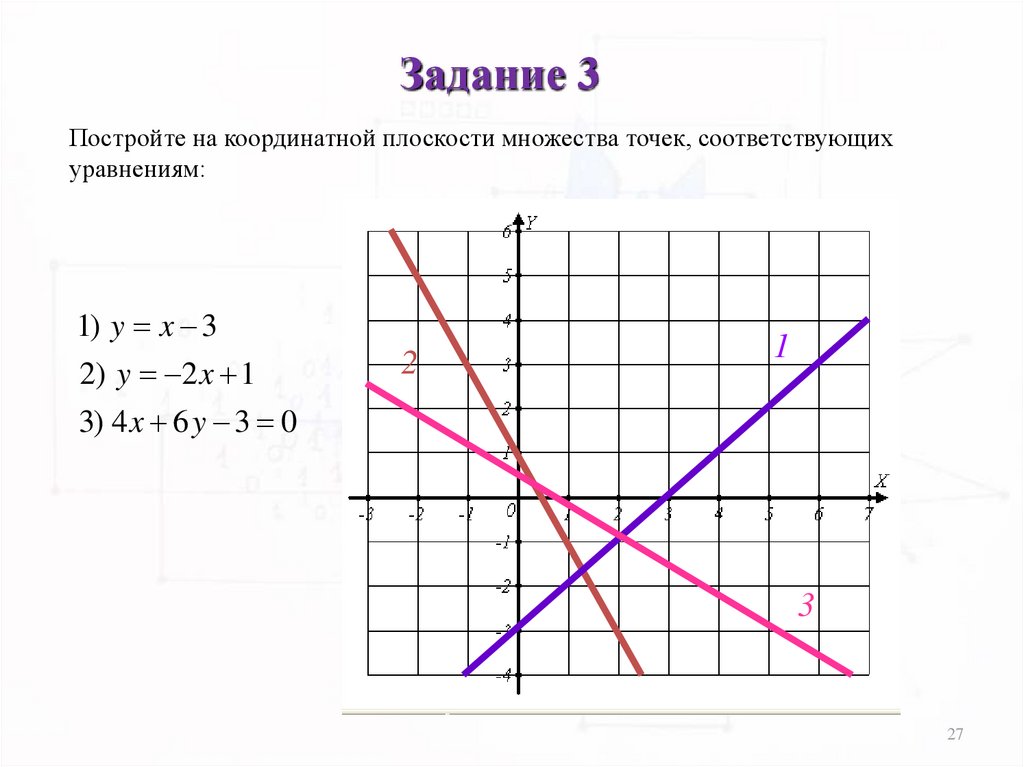
Задание 3
Постройте на координатной плоскости множества точек, соответствующих
уравнениям:
1) y x 3
2) y 2 x 1
3) 4 x 6 y 3 0
2
1
3
27

28.

Условие параллельности
прямых
Пусть заданы уравнения прямых:
l : y k1x b1
m : y k 2 x b2
l m, если k1 k2
Например:
a: y 2 x 5
b : y 2x 7
k1 k2 2 , то есть
a b
28

29.

Уравнение прямой, проходящей через две
заданные точки
Запишем уравнение
прямой, проходящей
через точки А и В:
y kx b
A( xA ; yA ), B( xB ; yB ),
Если прямая проходит через точки А и В, то координаты этих
точек можно подставить в уравнение прямой:
A : y A kxA b
B : yB kxB b
Получаем систему линейных
уравнений с неизвестными k
и b. Решив ее, находим
значения k и b.
29

30.

Уравнение прямой, проходящей через две
заданные точки
Запишем уравнение
прямой, проходящей
через точки :
y kx b
A( 2; 1), B(2; 3),
Подставим координаты в уравнение прямой:
1 2k b k 0,5
b
2
3
2
k
b
Решаем систему линейных
уравнений с неизвестными k Ответ: y 0,5 x 2
A : 1 k ( 2) b
B : 3 k 2 b
и b.
30

31.

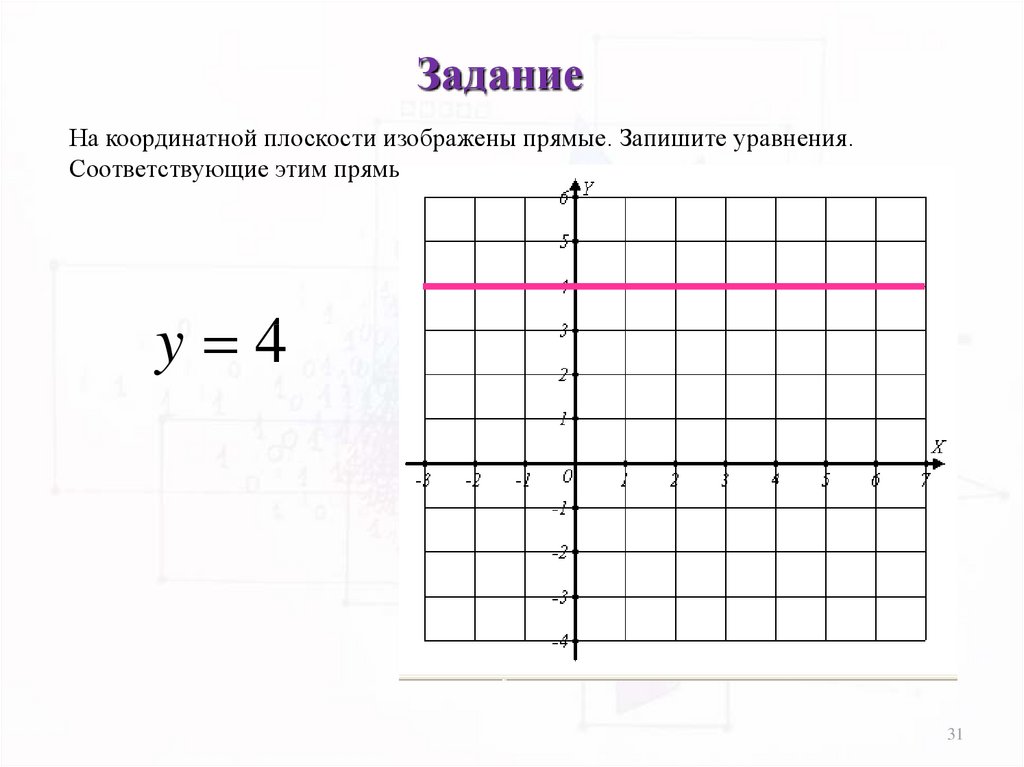
Задание
На координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
y 4
31

32.

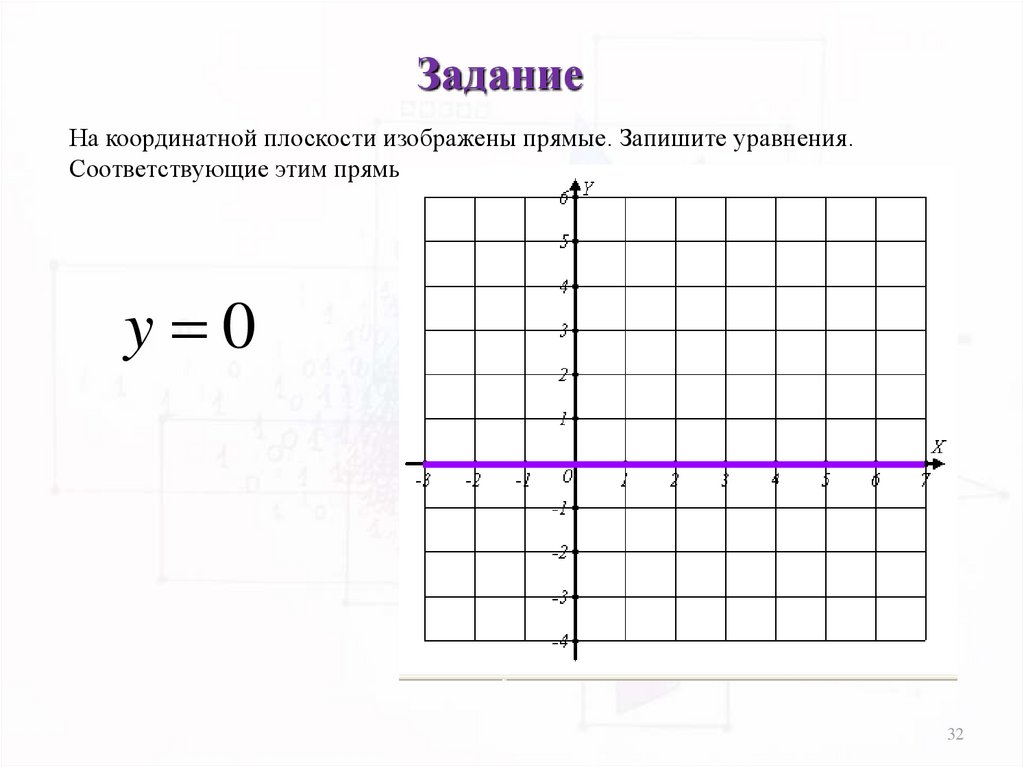
Задание
На координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
y 0
32

33.

Задание
На координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
x 4
33

34.

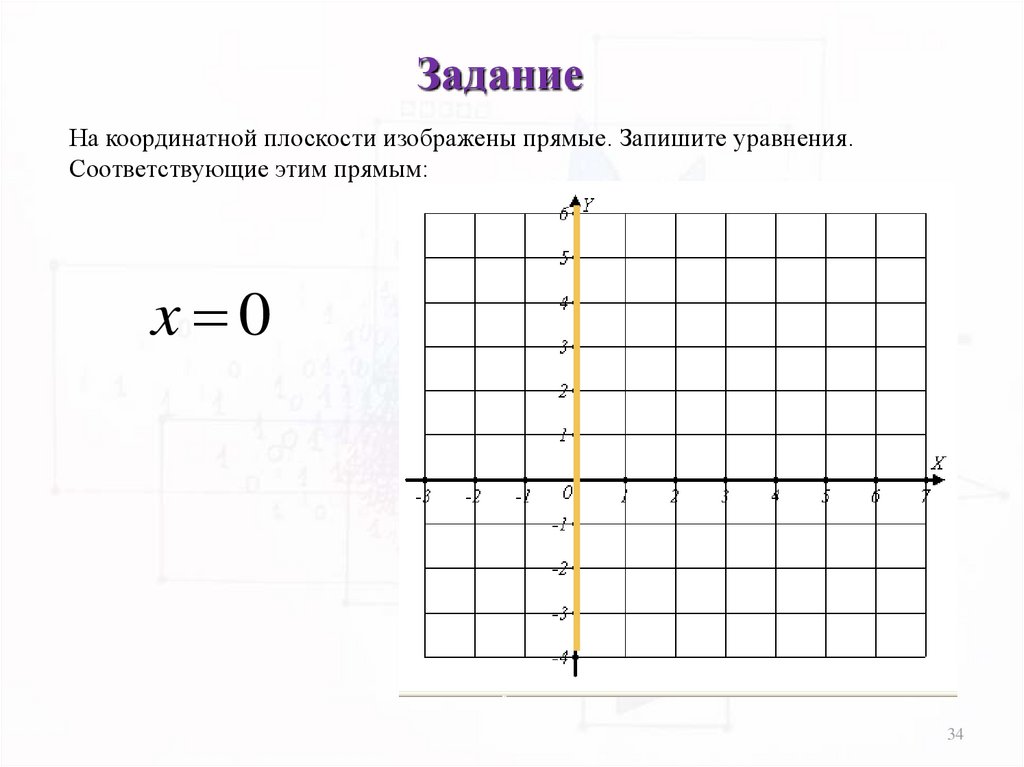
Задание
На координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
x 0
34

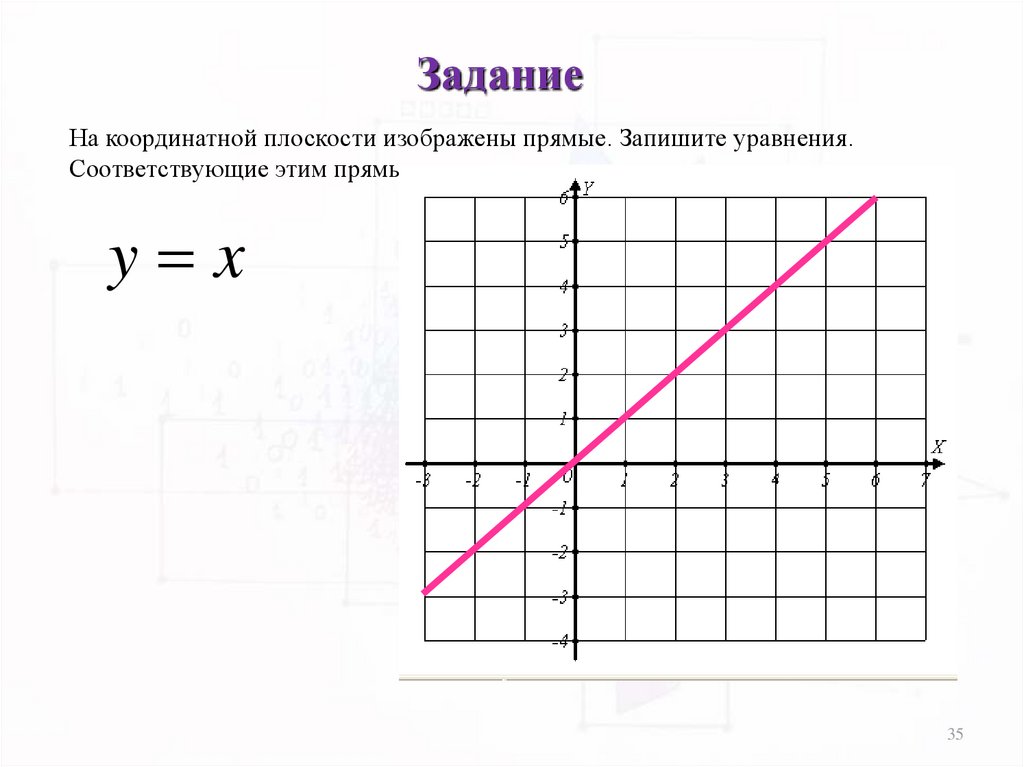
35.

Задание
На координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
y x
35

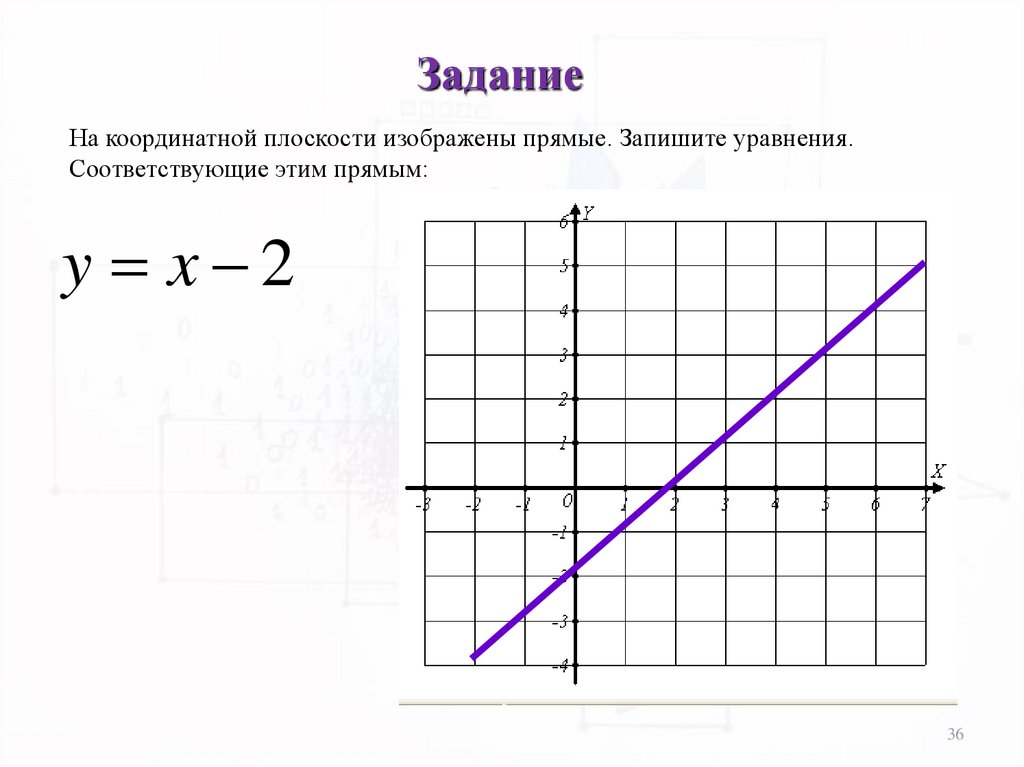
36.

Задание
На координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
y x 2
36

37.

Задание
На координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
y x 4
37

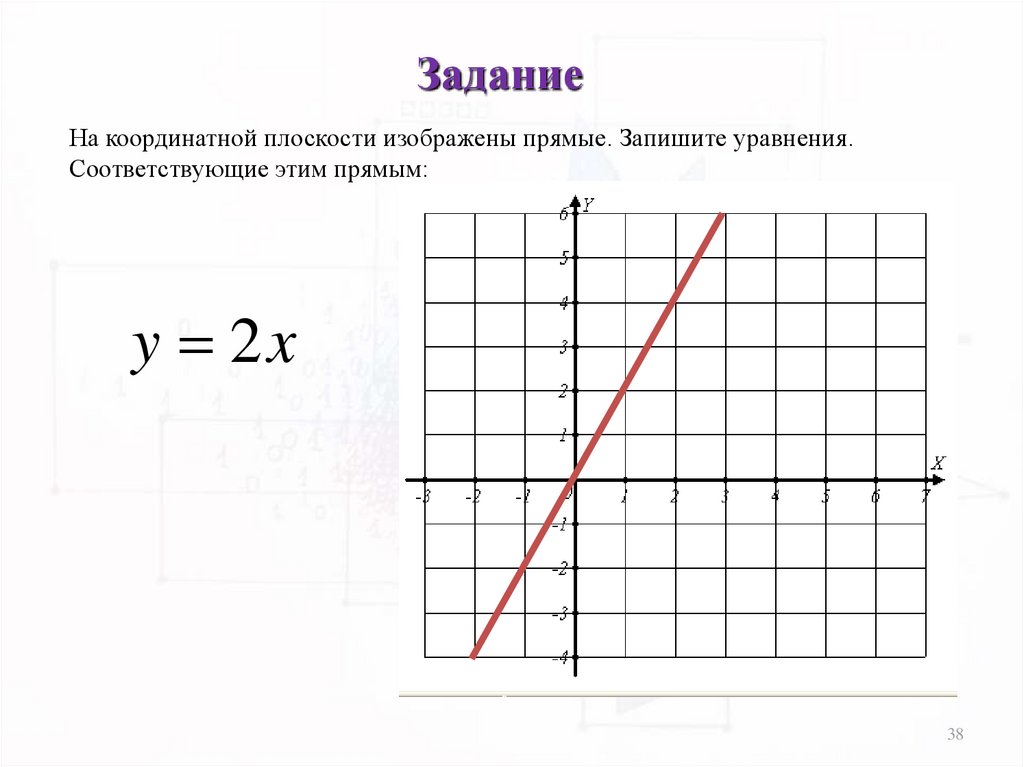
38.

Задание
На координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
y 2x
38

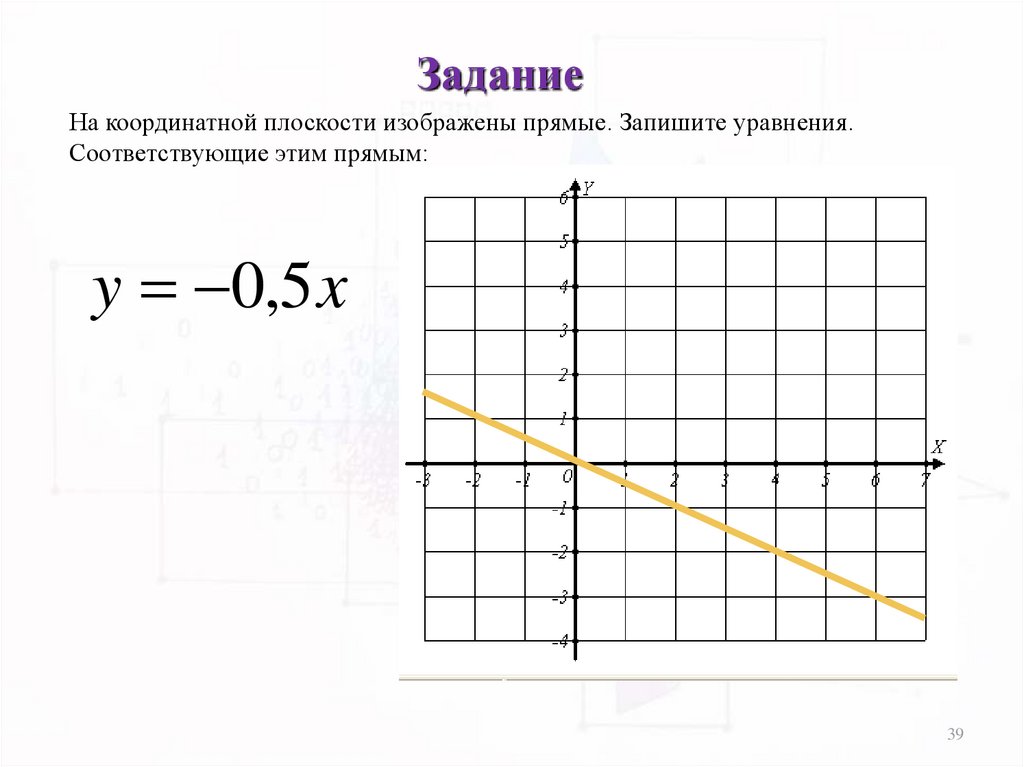
39.

Задание
На координатной плоскости изображены прямые. Запишите уравнения.
Соответствующие этим прямым:
y 0,5 x
39

40. Домашнее задание

№ 972(б), 973, 977, 978
Благодарю за внимание
40