Напряженное состояние в грунтах. (Лекция 5)

1. Л Е К Ц И Я №5 Напряженное состояние в грунтах

2. П л а н 5.1. Основы напряженного состояния грунтов оснований. 5.2. Фазы напряженного состояния грунта. 5.3. Расчетные модели грунтовых оснований

План
5.1. Основы напряженного состояния грунтов
оснований.
5.2. Фазы напряженного состояния грунта.
5.3. Расчетные модели грунтовых оснований.
5.4. Распределение напряжений от сосредоточенной силы (задача Буссинеска)
5.5. Распределение напряжений от действия
местной равномерно-распределенной нагрузки
(задача Лява).
5.6. Метод угловых точек.
5.7. Способ элементарного суммирования.

3.

5.1. Основы напряженного состояния
грунтов оснований
Распределение напряжений в грунтовой
толще зависит от следующих факторов:
- характера и режима нагружения массива;
- инженерно-геологических и гидрогеологических особенностей площадки строительства;
- состава и физико-механических свойств
грунтов.

4.

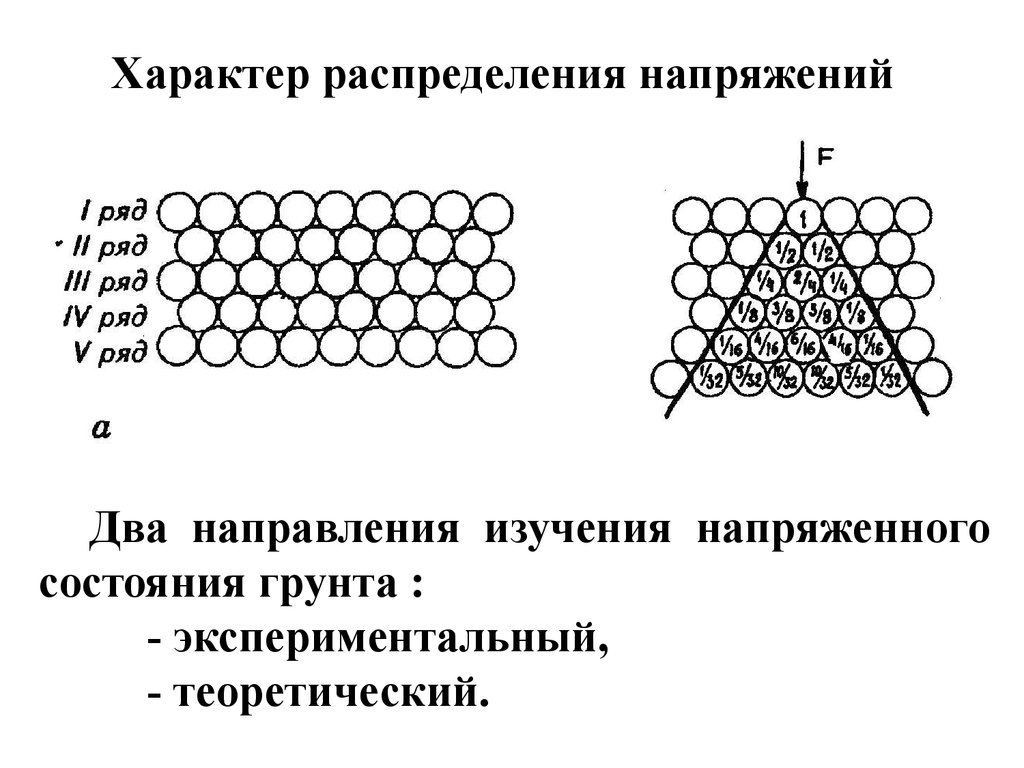
Характер распределения напряжений
Два направления изучения напряженного
состояния грунта :
- экспериментальный,
- теоретический.

5.

Отличия грунтов основания от материалов
строительных конструкций:
- малая прочность и большая деформируемость;
- деформация во времени при постоянной нагрузке
возрастает;
- неоднородность грунтов и их свойств в основании
фундаментов;
- неоднородность напряжений в грунтовой толще в
естественных условиях и сложность их измерений
под действием внешней нагрузки;
- различие закономерностей изменения напряженного состояния грунтов, однородных по составу,
но при различной величине внешней нагрузки.

6.

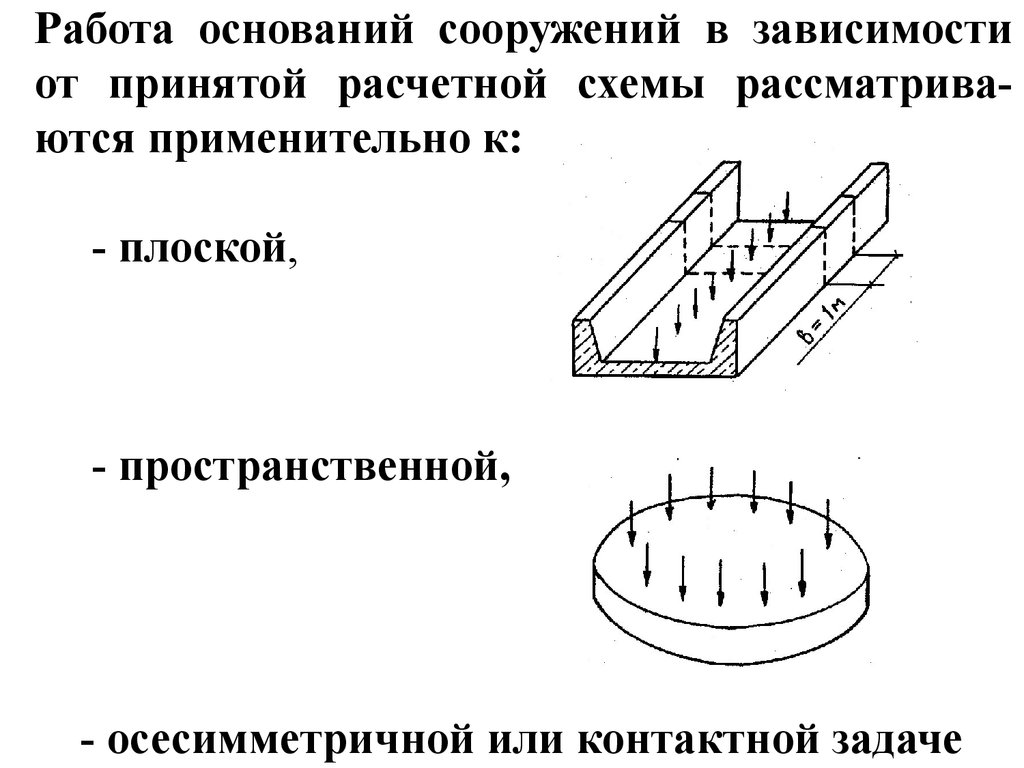
Работа оснований сооружений в зависимости
от принятой расчетной схемы рассматриваются применительно к:
- плоской,
- пространственной,
- осесимметричной или контактной задаче

7.

5.2. Фазы напряженного состояния грунта.
Д о п у щ е н и я Г е р с е в а н о в а,
позволяющие рассматривать грунт как линейнодеформируемую среду, т.е. применять теорию
упругости:
1. Давление на грунт не превышает величины начального критического Р Р кр.нач.
2. Грунт нагружается только один раз.
3. Грунт является сплошным телом.
4. Грунт является изотропным телом.

8.

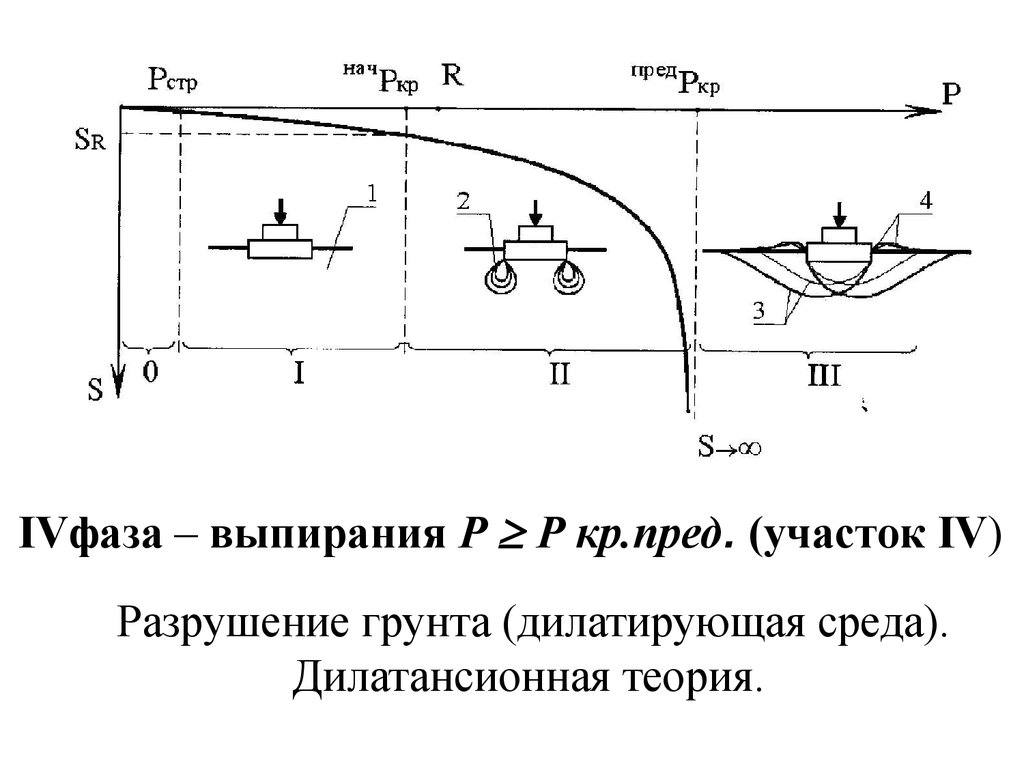
Фазы напряженного состояния грунта
1 - основание в допредельном состоянии, 2- зоны
сдвигов, 3-линии скольжения, 4 – линии выпоров

9.

I фаза - упругих деформаций (участок I)
Р себя
Рстр.
Рстр 10
кПа
Грунт0ведет
как упругое
тело,
применим закон Гука

10.

II фаза – уплотнения и местных сдвигов
Рстр < Р < Р кр.нач. (участок II)
При загрузке зависимость осадки от давления

11.

III фаза – интенсивных сдвигов (участок III)
Ркр.нач. Р <Ркр.пред. или Ркр.нач. Р < R
Zmax=0,25b
Грунт ведет себя как нелинейная среда
(упругопластическая), зависимость осадки
от давления не линейна. Необходимо пользоваться
теорией пластичности механики грунтов.

12.

Давление, соответствующее началу появления
областей пластических деформаций (сдвигов
и разрушения грунта) под краями фундамента,
называется начальным критическим давлелением, Р кр.нач.
Давление, соответствующее исчерпанию
несущей способности грунта основания, называется предельным критическим давлением,
Р кр. пред.

13.

IVфаза – выпирания Р Р кр.пред. (участок IV)
Разрушение грунта (дилатирующая среда).
Дилатансионная теория.

14.

С помощью теории упругости можно только
определить конечную осадку при Р Ркр.нач.
Несоблюдение этого условия может привести
к значительным ошибкам в расчетах.
Осадки во времени определяют с помощью
теории фильтрационной консолидации.

15.

5.3 Расчетные модели грунтовых оснований
Две группы:
- линейные модели, в которых
зависимость между напряжениями и
деформациями является линейной;
- нелинейные, в которых эта зависимость
является нелинейной

16.

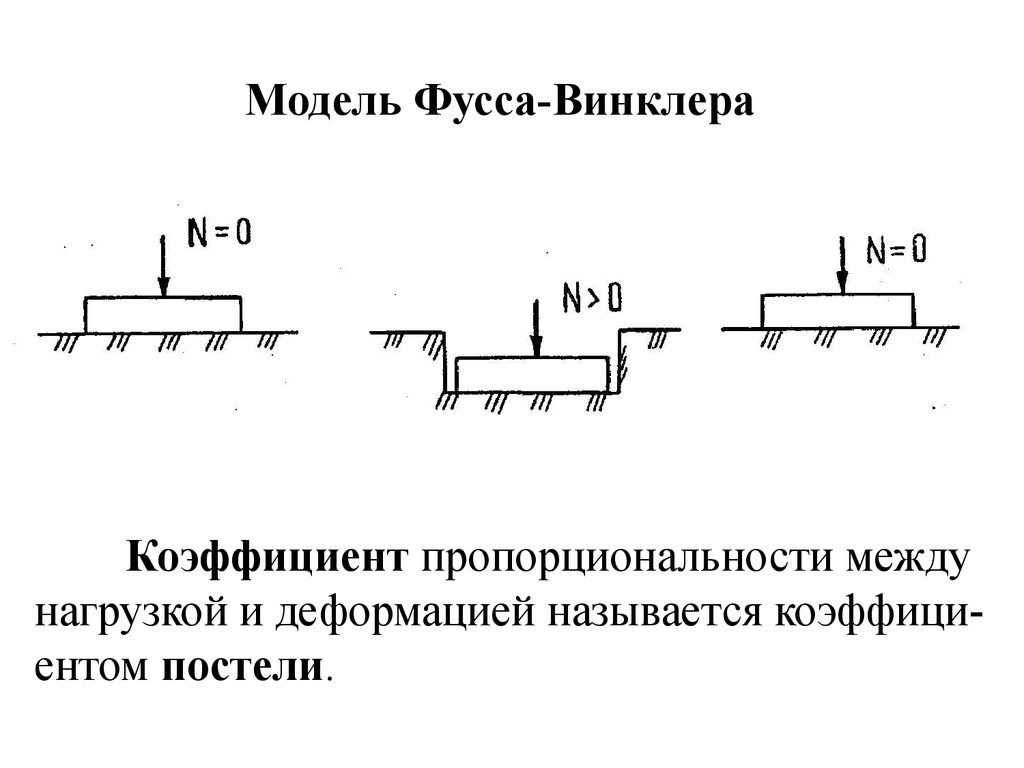
Модель Фусса-Винклера
Коэффициент пропорциональности между
нагрузкой и деформацией называется коэффициентом постели.

17.

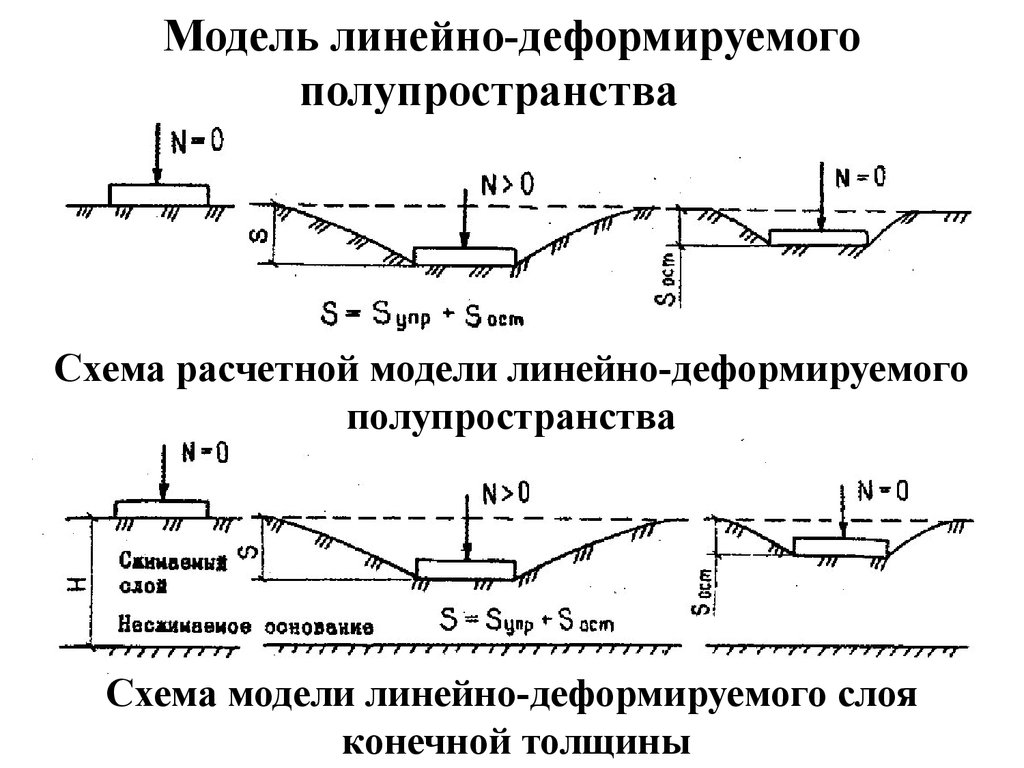
Модель линейно-деформируемого
полупространства
Схема расчетной модели линейно-деформируемого
полупространства
Схема модели линейно-деформируемого слоя
конечной толщины

18.

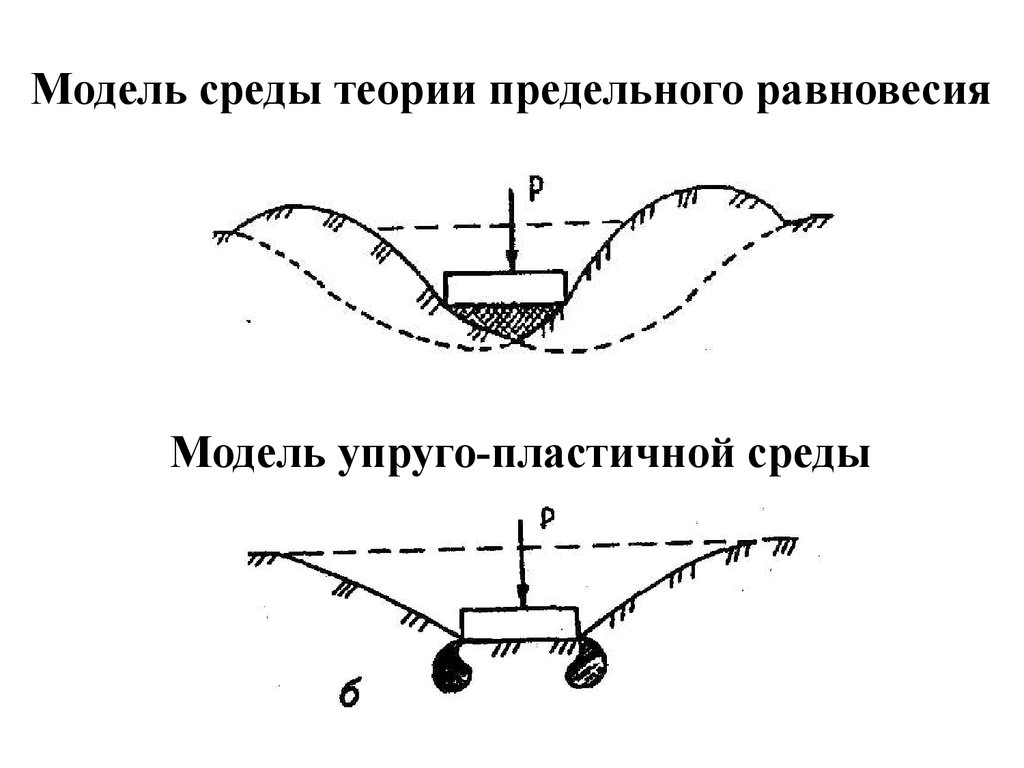
Модель среды теории предельного равновесия
Модель упруго-пластичной среды

19.

5.4. Основная пространственная задача
Ж. Буссинеска - распределение напряжений
от сосредоточенной силы
z у х ух ху zx xz zy yz

20.

Схема к определению напряжений при
действии сосредоточенной силы
Задача заключается в
определении всех составляющих напряжений
z x y zх zу хy а также
перемещений wz wx wy для
любой
точки
полупространства, имеющей координаты Z, У, Х
или R и .

21.

Схема распределения напряжений по
полушаровой поверхности с радиусом R
Угол - угол видимости
Чем дальше от точки приложения силы Р
будет расположена точка М тем меньше будет ее
перемещение. При R= перемещение точки М
будет равно нулю dR=0.

22.

При одном и том же значении R для различных
величин угла перемещения точки будут неодинаковы.
Наибольшее перемещение получит точка, расположенная по оси z, т.е. =0.
С увеличением угла перемещения по направлению радиуса R уменьшаются, и в случае =900
(на поверхности грунта) при малых деформациях
будут равны нулю.
В точке приложения силы, где R=0 следует
z = .

23.

Приняв как постулат, что R прямо пропорционально cos и обратно R2, можно записать зависимость
Cos
(1)
R
2
R
где а - коэффициент, определяемый из условия
равновесия внутренних и внешних сил по схеме
радиальных напряжений при действии сосредоточенной силы
Р- R=0
3 Р
Тогда можно записать
2
(2)

24.

Подставив в формулу (1) а, получим формулу
Буссинеска - векторного напряжения в любой
точке пространства от действия сосредоточенной
нагрузки в однородных грунтах
3 Р
R 2 Cos
2 R
(3)

25.

Вертикальные нормальные напряжения
3
3 Р Z
Z 5
2 R
(4)
Касательные напряжения
ХZ
УZ
2
3 Р Z X
5
2 R
(5)
2
3 Р ZУ
5
2 R
(6)

26.

R z r
2
2
2
r
2
2
R z r z 1
z
2
1
2
(7)
Подставив в формулу вертикальных нормальных
напряжений вместо R получим:
Z
3
r
2 1
z
2
5
2
Р
2
z
(8)

27.

обозначив
К
формула примет вид:
3
r 2
2 1
z
5
2
Р
Z К 2
z
(9)
(10)
где К – коэффициент рассеивания напряжений,
определяется для ряда значений r/z
r – расстояние по горизонтали от оси Z,
проходящей через точку приложения
сосредоточенной силы
z – глубина рассматриваемой точки.

28.

Перемещения, параллельные осям координат:
по оси х
Р ( 1 v ) xz
x
wx
( 1 2v )
(11)
3
2 E R
R( R z )
по оси у
Р ( 1 v ) yz
y
wy
2( 1 v )
(12)
3
2 E R
R( R z )
по оси z
Р( 1 v ) z
1
w
3 2( 1 v )
2 E R
R
2
(13)

29.

Напряжения от действия группы сил
Р1 =Р2=Р3, R1 < R2 < R3, r1<r2<r3, z1=z2=z3, z1> z2> z3
Р3 1 n
Р1
Р2
Z K 1 2 K 2 2 K 3 2 2 K i Рi
z
z
z
z i 1
К - определяют в зависимости от ri / z
по таблице (или формуле)

30.

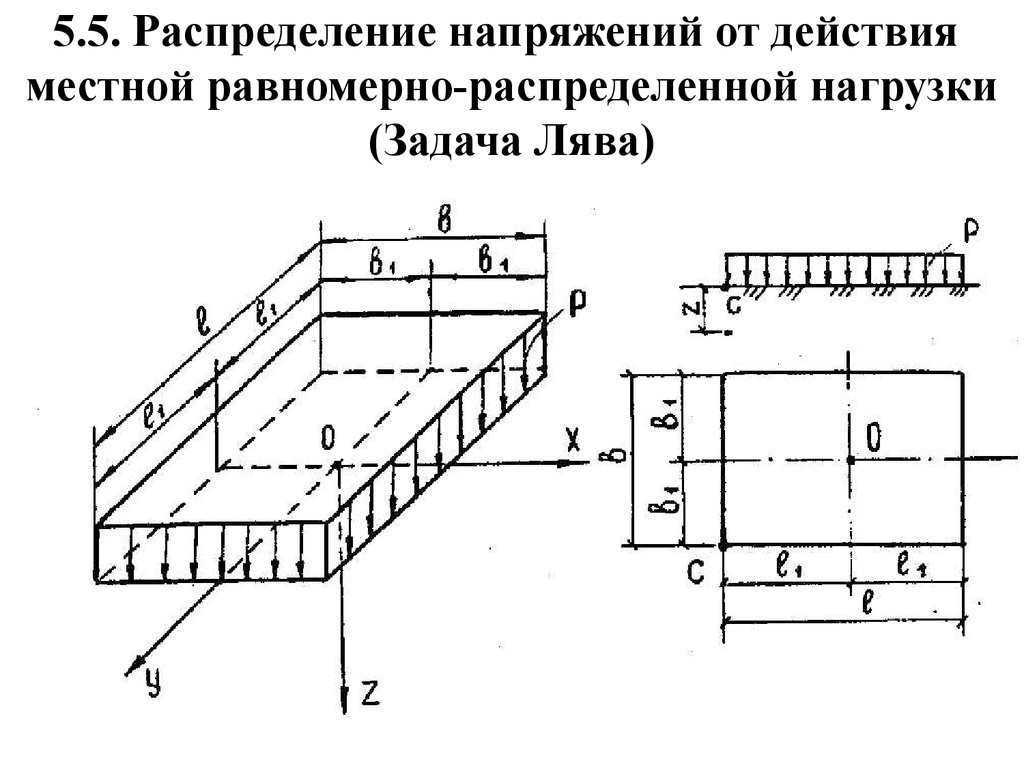
5.5. Распределение напряжений от действия
местной равномерно-распределенной нагрузки
(Задача Лява)

31.

Для точек, расположенных на вертикали, проходящей
через центр загруженной площади, формула имеет
вид:
2
2
2
2
Р
l
b
l
b
z
l
b
2
z
1 1
1 1
1
1
Z0
arctg
2
2
2
2
2
2
2
2
2
2
z l1 b1 z
l1 z b1 z b1 l1 z
Для точек, расположенных на глубине на прямых,
проходящих через углы загружаемой площади, угловое напряжение определяется по формуле:
2
2
2
2
Р
4
l
b
4
l
b
z
4
l
4
b
2
z
c
1 1
1 1
1
1
Z
arctg
2
2
2
2
2
2
2
2
2
2
z 4l1 4b1 z
4l1 z 4b1 z 4b1 4l1 z

32.

Сжимающие напряжения, возникающие под
центром О прямоугольной площади, загруженной
равномерной распределенной нагрузкой:
z =К р
где К – коэффициент, принимаемый по табл.СНиП
как функции относительной глубины =2z/b
или =z/b и соотношению сторон прямоугольной площади загрузки =l/b принимают
в зависимости от величин
К=f(2z / b, l / b) = l / b и = 2z / b
где l – длинная сторона прямоугольной площади
загружения; b - ее ширина.
р - равномерно-распределенное давление.

33.

Напряжение под угловыми точками определяют
по формуле:
z =0,25К р
К - коэффициент рассеивания напряжений для
угловых точек, определяются по таблицам СНиП
или любого учебника в зависимости от величин
= l / b и = z / b.
Формула z =0,25К р – используется для
определения влияния фундаментов друг на друга.

34.

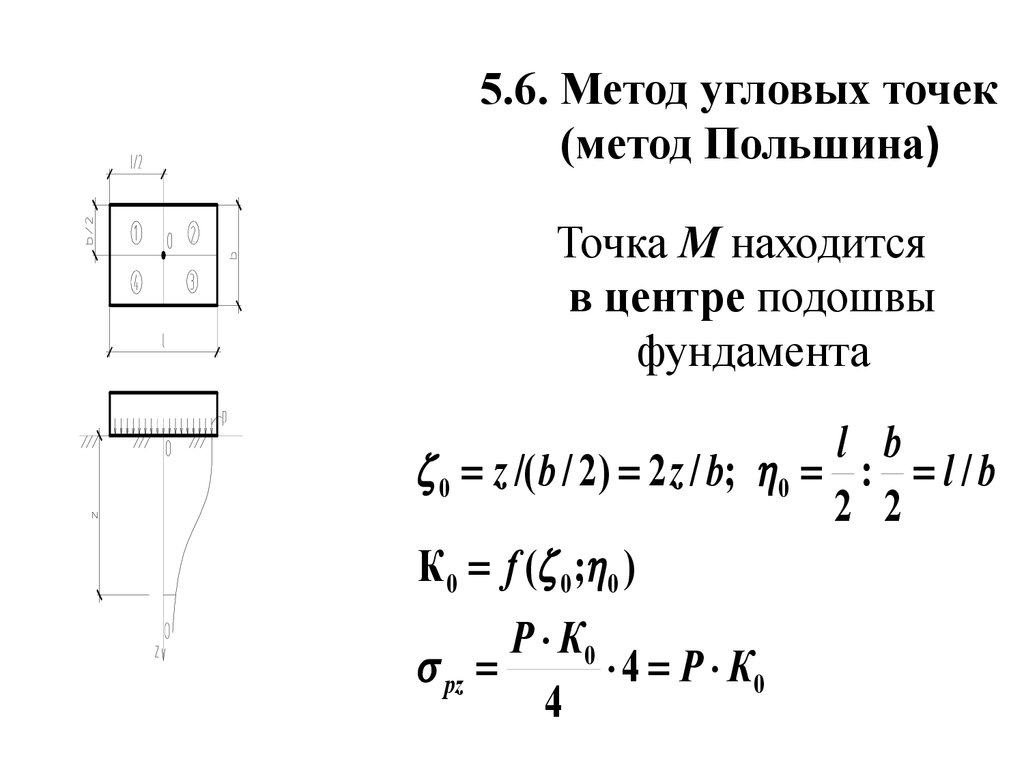
5.6. Метод угловых точек
(метод Польшина)
Точка М находится
в центре подошвы
фундамента
l b
0 z /( b / 2) 2 z / b; 0 : l / b
2 2
К 0 f ( 0 ; 0 )
P К0
pz
4 P К0
4

35.

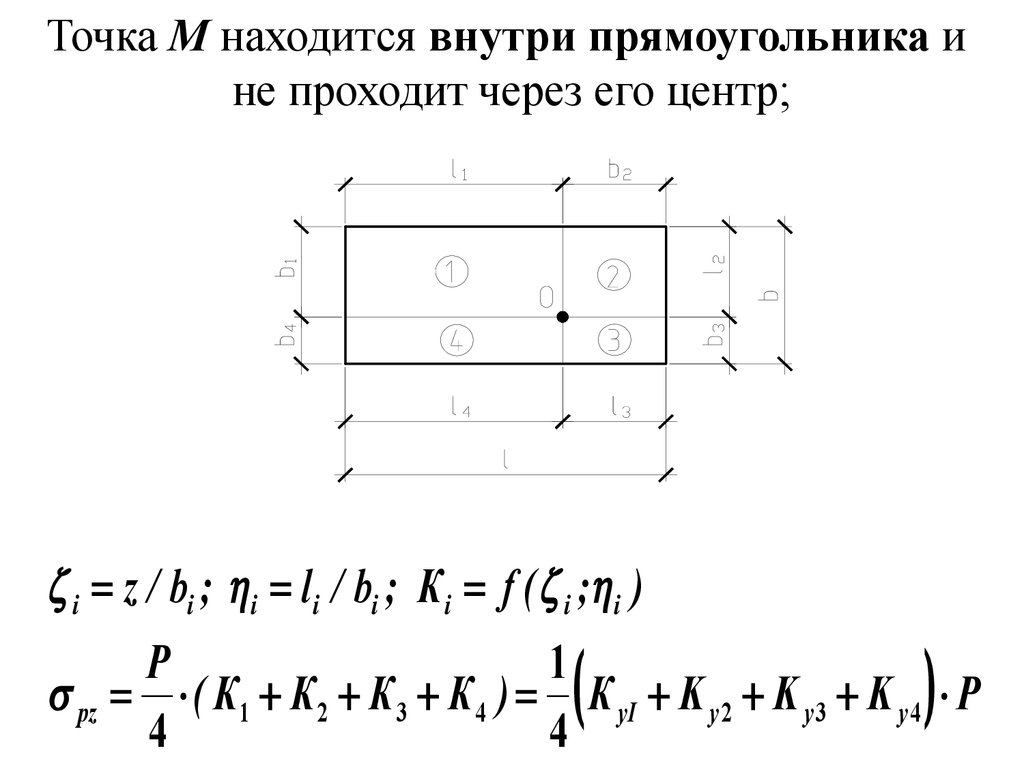
Точка М находится внутри прямоугольника и
не проходит через его центр;
i z / bi ; i l i / bi ; К i f ( i ; i )
P
1
pz ( К1 К 2 К 3 К 4 ) К уI K y 2 K y 3 K y 4 P
4
4

36.

Точка М расположена за пределами контура
прямоугольника загружения
P
1
pz ( К1 К 2 К 3 К 4 ) K y1 K y 2 K y 3 K y 4 P
4
4
z l1
К1 f ; ; К 2
b1 b1
z l2
f ; ; К 3
b2 b2
z l3
f ; ; К 4
b3 b3
z l4
f ; ;
b4 b4

37.

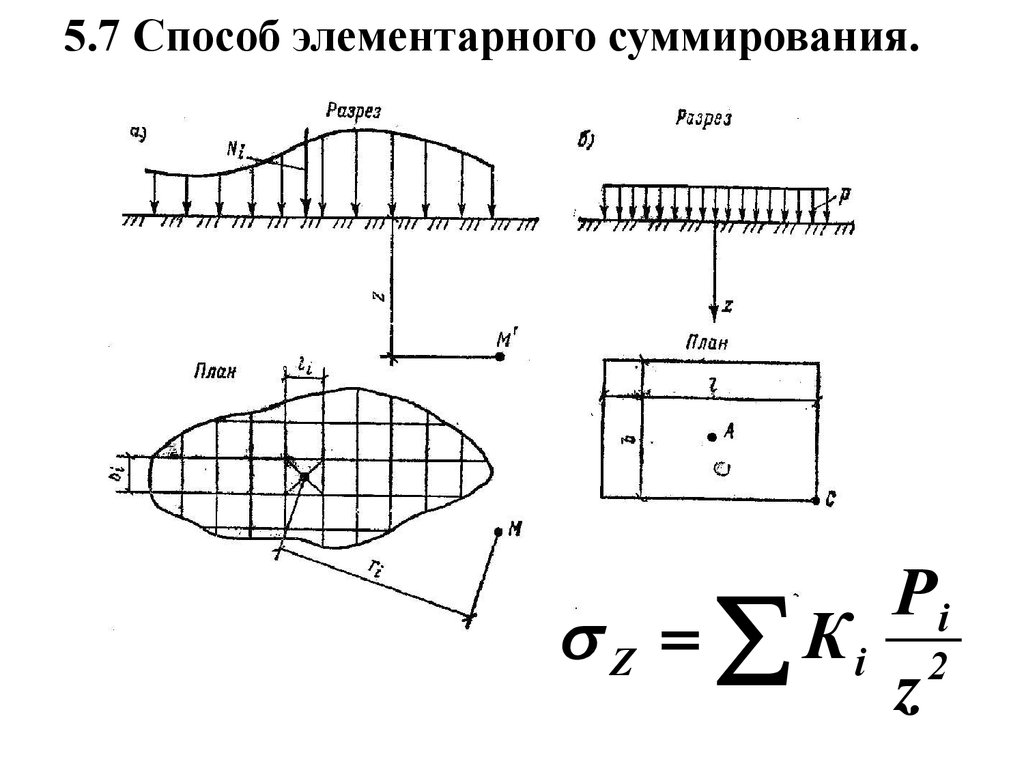
5.7 Способ элементарного суммирования.
Рi
Z Кi 2
z