Понятия о напряжениях

1. Лекция № 3

1

2. Понятия о напряжениях.

n
B
А
F
2

3.

Выделим в сечении малую
площадку А в окрестности точки
B с нормалью n, в которой
действует сила F. За среднее
напряжение
на
площадке
принимаем отношение
F
pср
A
3

4.

В пределе получаем:
F
pn lim
A 0 A
где pn – полное напряжение в точке B.
Размерность напряжений:
pn Н
м Па
2
4

5.

Напряжением называется
интенсивность внутренней силы в
данной точке поперечного сечения
Напряжение - это количественная мера
интенсивности внутренних сил.
Напряжение, как векторная величина,
может быть представлено нормальной
и касательной составляющими
(по отношению к площади сечения).
5

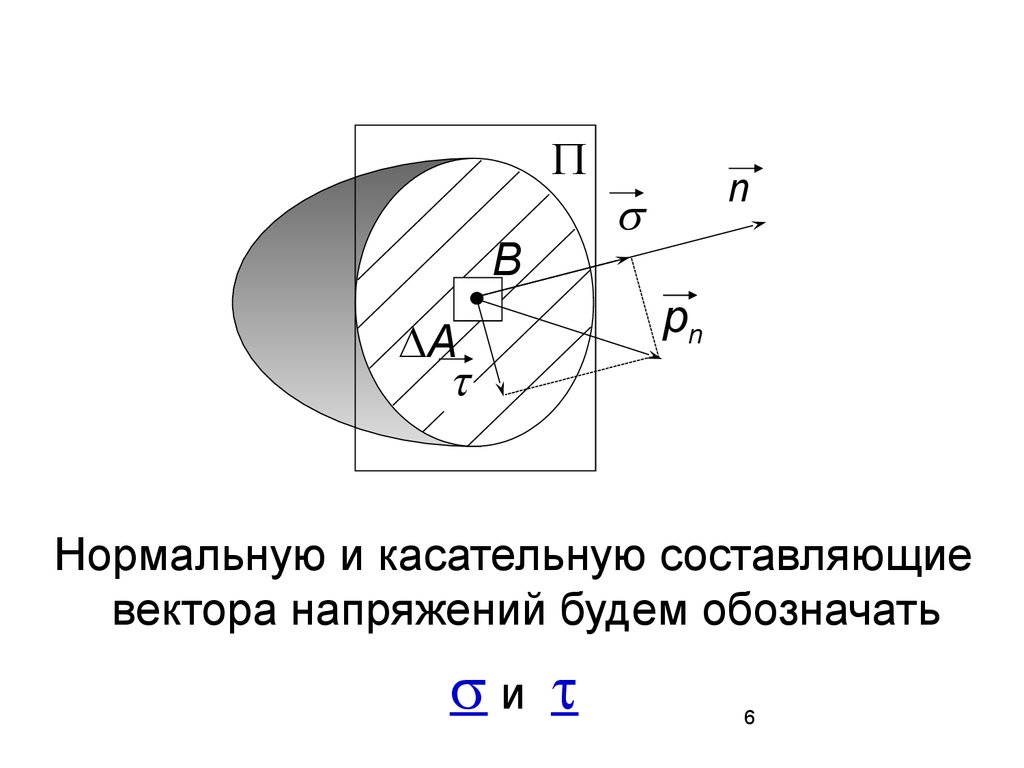
6.

В
А
n
pn
Нормальную и касательную составляющие
вектора напряжений будем обозначать
и
6

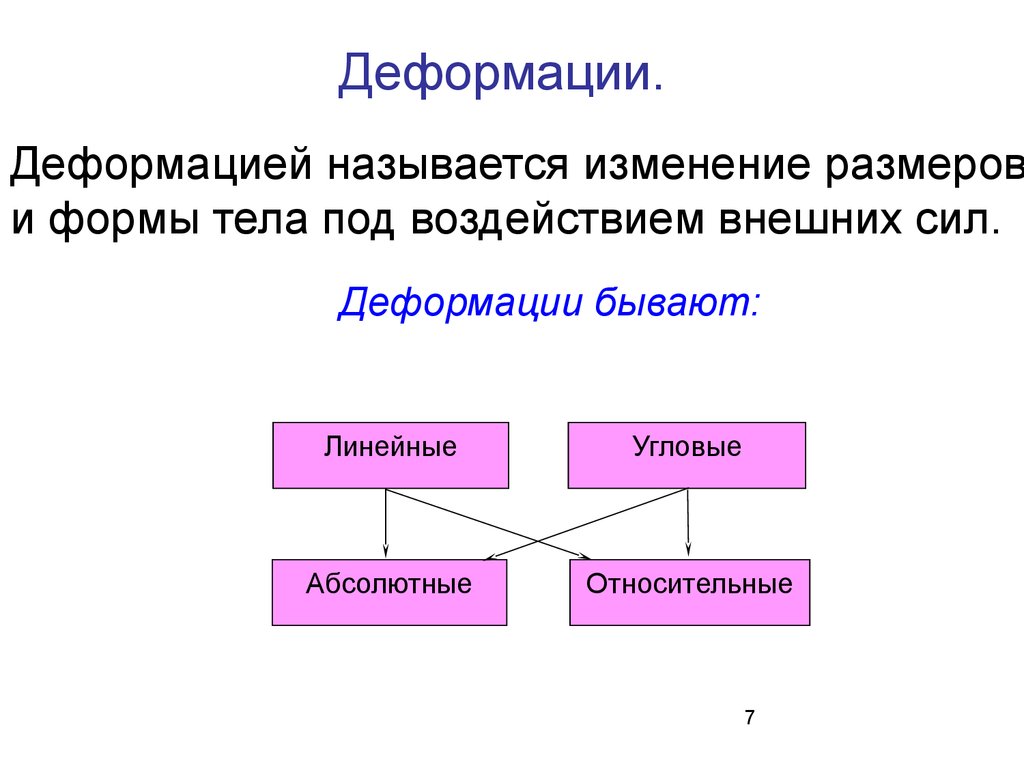
7.

Деформации.
Деформацией называется изменение размеров
и формы тела под воздействием внешних сил.
Деформации бывают:
Линейные
Угловые
Абсолютные
Относительные
7

8.

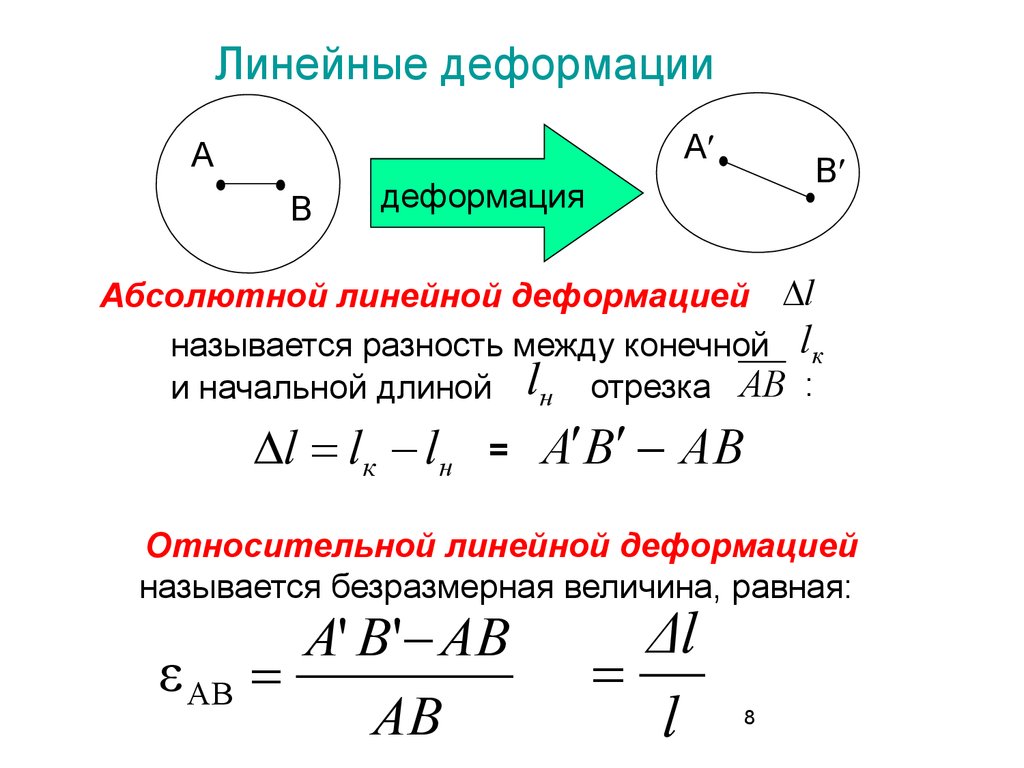
Линейные деформации
A
A
B
B
деформация
Абсолютной линейной деформацией l
называется разность между конечной lк
и начальной длиной lн отрезка AB :
=
l l к l н
А В АВ
Относительной линейной деформацией
называется безразмерная величина, равная:
ε AB
A' B ' AB
AB
Δl
l
8

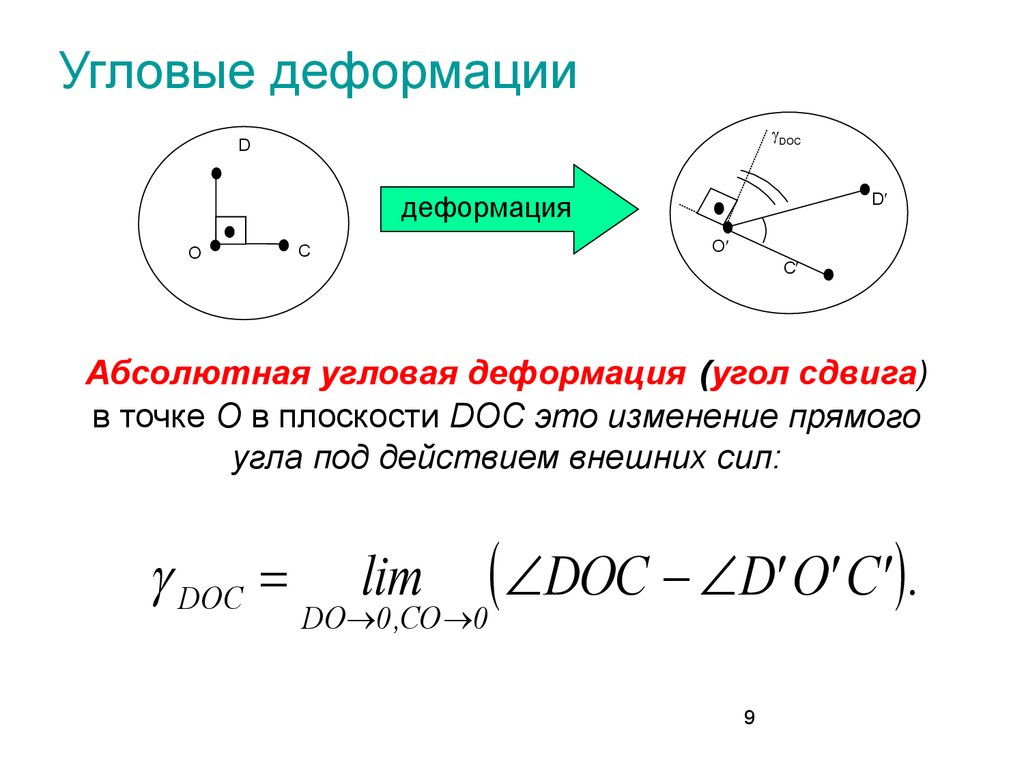
9. Угловые деформации

DOC
D
D
деформация
O
O
C
C
Абсолютная угловая деформация (угол сдвига)
в точке О в плоскости DOC это изменение прямого
угла под действием внешних сил:
DOC
DOC D' O' C' .
DO 0 ,CO 0
lim
9

10.

S
a
F
F
Относительной угловой деформацией (углом сдвига)
называется отношение полной деформации ∆S к
расстоянию между сдвигающимися плоскостями а:
S
tg
a
т.к.
0,
то:
tg
10

11.

РАСТЯЖЕНИЕ – СЖАТИЕ ПРЯМОГО БРУСА.
Растяжение – сжатие, это способ
нагружения стержня, при котором
внутренние силы в поперечном
сечении приводятся к силе,
перпендикулярной поперечному
сечению и приложенной в центре
тяжести сечения.
11

12.

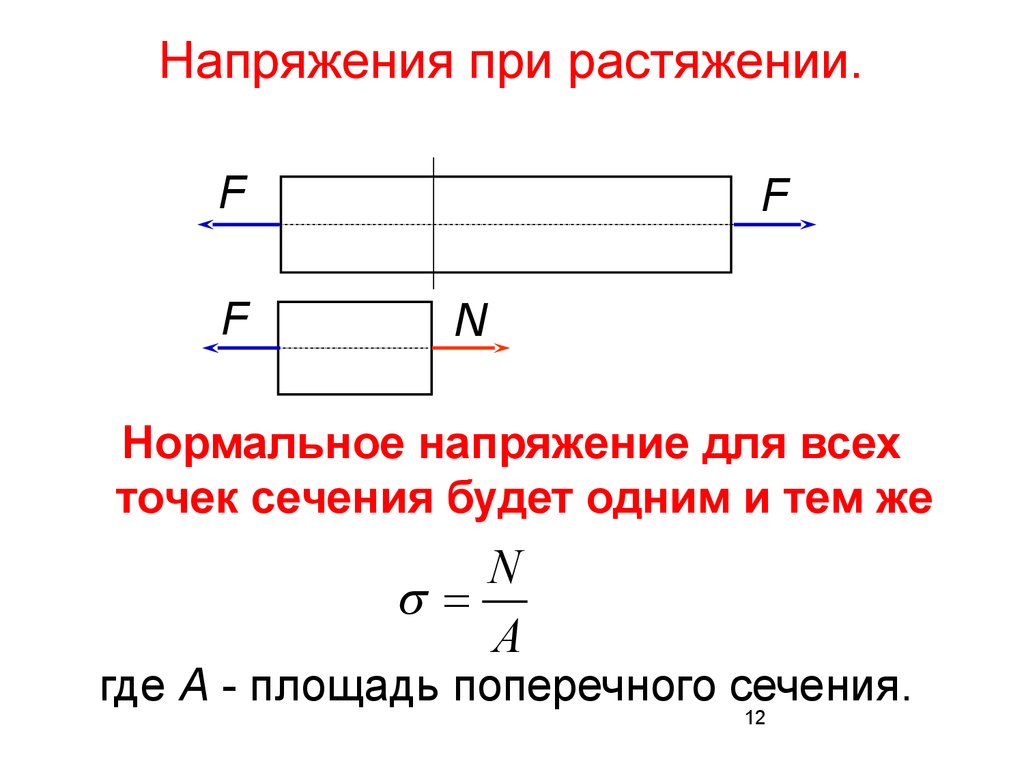
Напряжения при растяжении.
F
F
F
N
Нормальное напряжение для всех
точек сечения будет одним и тем же
N
А
где A - площадь поперечного сечения.
12

13. Закон Гука при растяжении.

В упругой области нагружения
существует прямая пропорциональная
зависимость между относительной
линейной деформацией и нормальным
напряжением.
σ Еε
13

14.

где: Е – модуль Юнга – модуль
продольной упругости (модуль упругости
первого рода) - справочная величина,
для каждого материала своя и
неизменная.
Размерность:
Н
Е 2 Па
м
Естали = 2 105 МПа;
Еалюминия = 0,8 105 МПа.
- относительная линейная упругая
деформация. Величина безразмерная.
14

15.

1
1
Диаграммы линейного
деформирования
2
1 – сталь;
2 – алюминий.
2
0,002
Экспериментально показано, что стали = 0,002.
Чем пластичнее материал, тем меньше угол .
15

16.

Закон Пуассона.
F
F
a
y
a- a
x
b- b
b
Δl
ε
- относительная продольная деформация
l
Δb
εx
b
Δa
εy
a
- относительная поперечная деформация
ε x ε y ε
- показано экспериментально
16

17.

Отношение поперечной деформации к
продольной деформации – величина
постоянная для любого материала и её
абсолютное значение называется
коэффициентом Пуассона.
0 ≤ μ ≤ 0,5
– для любого
изотропного
материала
μ пробки = 0;
μчугуна = 0,23 ÷ 0,27;
μстали = 0,29 ÷ 0,33;
μмеди = 0,31 ÷ 0,33;
µкаучука = 17
0,47.

18. Выведем формулу Гука для полной линейной деформации

q
q
N(z)
dz
(dz)
l
N(z)
dz
z
l
Для участка длиной dz имеем:
N z
σ
А
Δ dz
ε
dz
18
(dz)

19. Подставим эти соотношения в закон Гука:

N z
Δ dz
E
A
dz
N z
l
dz
EА
z
Nl
l
EА
N z
dz
dz
EА
0
0
l
l
формула Гука для стержня с
распределенной нормальной
нагрузкой
формула Гука для стержня с
постоянной нормальной
нагрузкой
Для стержня, имеющего n различных участков, получаем:
N zi
l
dzi
EА
i 1 i i
n
EА - жесткость при растяжении-сжатии
19

20.

ql
Пример:
определить
удлинение стержня l,
под
воздействием
распределенной силы q.
0 z l
N(z) = qz ,
N(0) = 0 ,
N z
l
dz
EА
0
ql
z
+
q
l
z
0 z l
N(z ) = ql-qz ,
N(0) = ql ,
N(l) = 0 .
N(l) = ql .
l
N
ql qz
0 EА dz
l
2
l
ql
qz
qlz l q z l
ql 2
dz dz
I
I
EА
EА
EА 0 2 EА 0 202 EА
0
0
l
ql 2
2 EF

21.

Напряжения в наклонных сечениях при
растяжении-сжатии
0 против хода
часовой стрелки
n1
n
0
n0
n1
р
n0
n1
n1
n0
Рассмотрим
стержень,
нагруженный
растягивающей силой N. Определим
напряжения, возникающие в наклонном
сечении n1 – n1.Воспользуемся методом
сечений.
А – площадь поперечного сечения n0 – n0.
N
N
Тогда площадь наклонного сечения n1
– n1 будет равна:
А
А
Cos
При равномерном распределении
сил упругости, полное напряжение р
в наклонном сечении будет равно:
Т.к.
N
А
p
N
А
NCos
Cos
А
21

22.

Определим нормальные
и касательные
напряжения в наклонном сечении n1 – n1 :
р
2
Cos
Cos
Cos
pCos
Sin 2
pSin Sin Cos
2
т.к.
С
внутренняя нормаль
2 Sin Cos Sin 2
Итак, получено:
Cos
2
Sin 2
2
Следствие:
max; 0
max
при = 0 , т.к. Cos0 = 1
при = 45 , т.к. Sin90 = 1
22

23.

Вывод:
максимальные
касательные
напряжения
возникают на площадках, расположенных под
углом 45 к нормали поперечного сечения
стержня.
Пример:
разрушение чугунного образца происходит
по площадкам максимальных касательных
напряжений.
23

24.

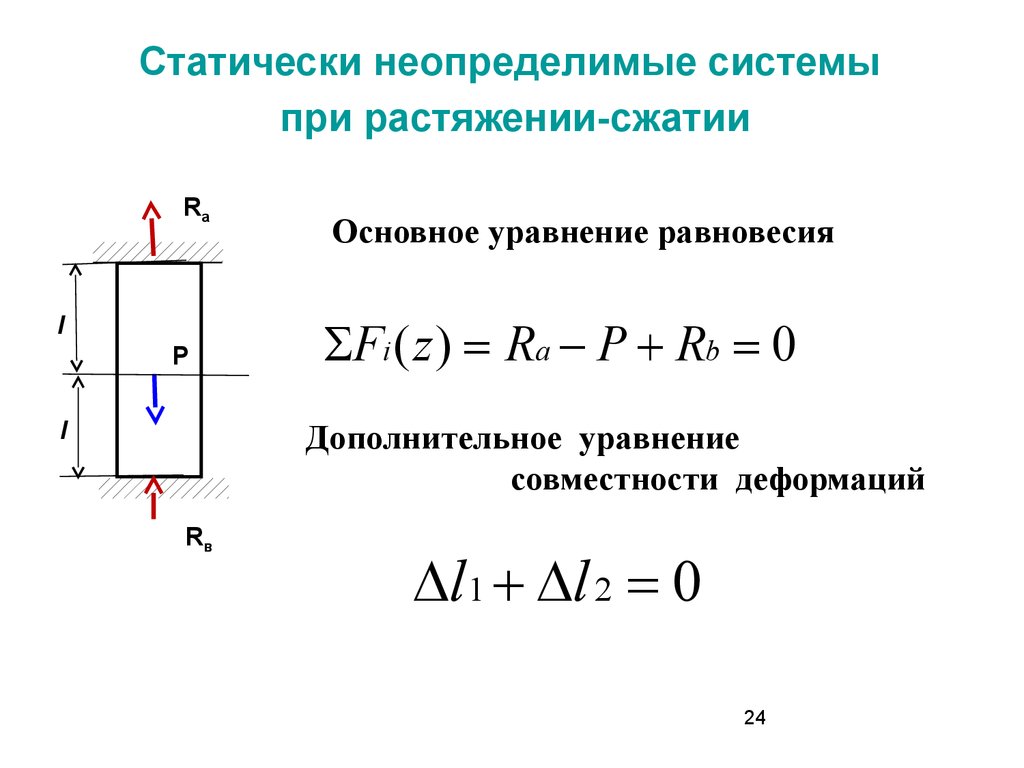
Статически неопределимые системы
при растяжении-сжатии
Ra
l
Р
l
Основное уравнение равновесия
Fi ( z ) Ra P Rb 0
Дополнительное уравнение
совместности деформаций
Rв
l1 l 2 0
24

25.

Изменение длины стержня при нагревании
Абсолютное удлинение стержня длиной l при
повышении его температуры на t определяется
по формуле:
l tl,
где
- линейный коэффициент температурного
расширения материала, (1/град)
25