Похожие презентации:
Дифференциал функции
1. Математический анализ
Лекция -5(ю)Дифференциал функции
1
2.
Предел функцииПовтор лекции 2
определена
Пример :
f ( x)
3
1
x sin x
в точке x = 0 не определена , но
lim f ( x) 2 0
x 0
3.
Первый замечательный пределРассмотрим окружность единичного радиуса, х - центральный угол, 0 < x <
Повтор лекции 2
/2
3
4.
Повтор лекции 2.
1
При этом xn xn 1 , т.е. последовательность {xn } 1
n
возрастает и она ограничена :
xn 2
1
1
1
2 ... n 1 2
1
2 2
2
1 (1 1 )
2
2n 1
1 12
следовательно 2 xn 3 , n
3
n
1
2 n. 1
4
5.
Повтор лекции 25
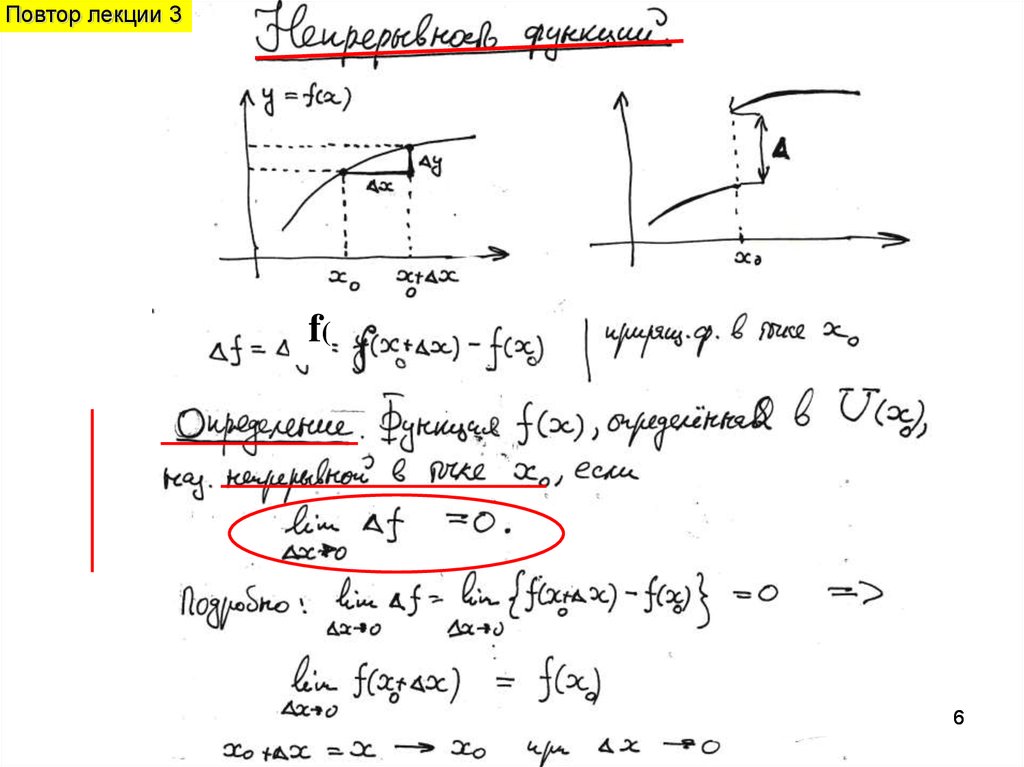
6.
Повтор лекции 3f(
6
7.
Повтор лекции 3.
10
10
7
8.
Повтор лекции 31
5
2
3
4
8
9.
Повтор лекции 3.
9
10. Точка разрыва первого рода – существование обоих односторонних конечных пределов
Рис. 9.411. Продолжение.
Если11
11
12.
Примеры13.
1314. .
1415.
1516.
Производная функцииВ
16
17. Понятие производной
1718. .
Таким образом, приходим к важнейшему понятию :Определение.
Пусть ф. f(x) определена в окр. т. x U(x)
Процедура вычисления производной наз.
дифференцированием
18
19. .
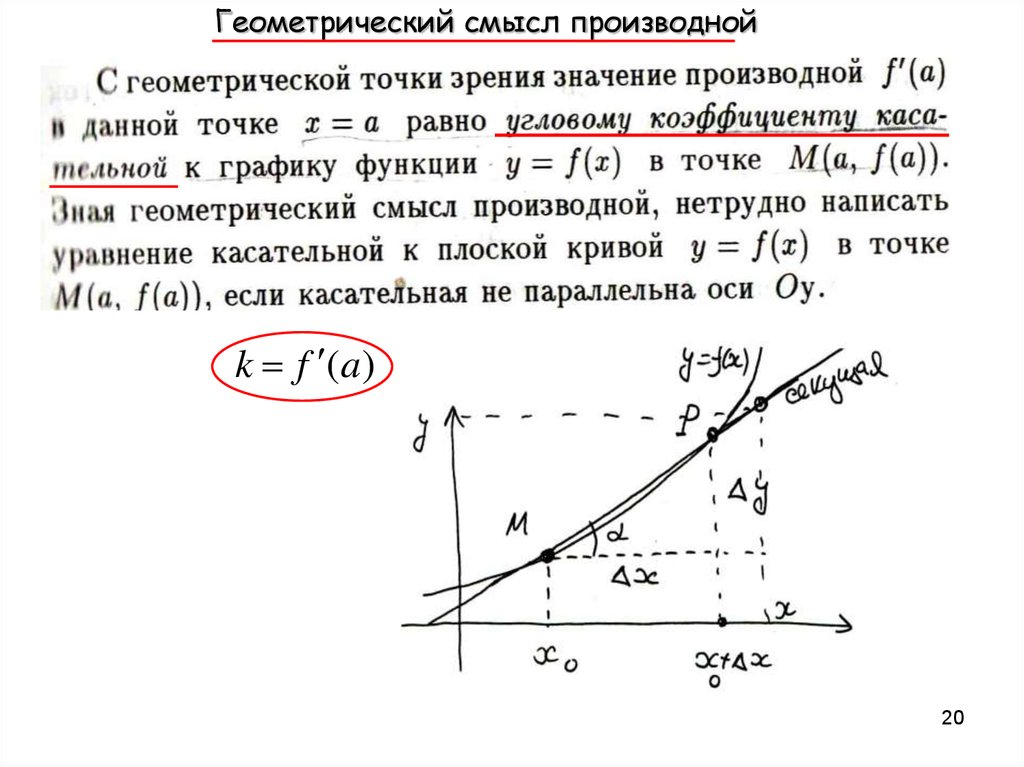
наз. предельное положение секущей при PM
k
f (a)
19
19
20.
Геометрический смысл производнойk f (a)
20
21.
Основные правила дифференцирования21
22.
2223.
Производная обратной функцииТогда
23
24.
2425.
Продолжение25
26.
2626
27.
2728.
Дифференциал функции28
29.
30. Экстремум функции
31.
Основные теоремы дифференциального исчисления____________
____________________________________________
31
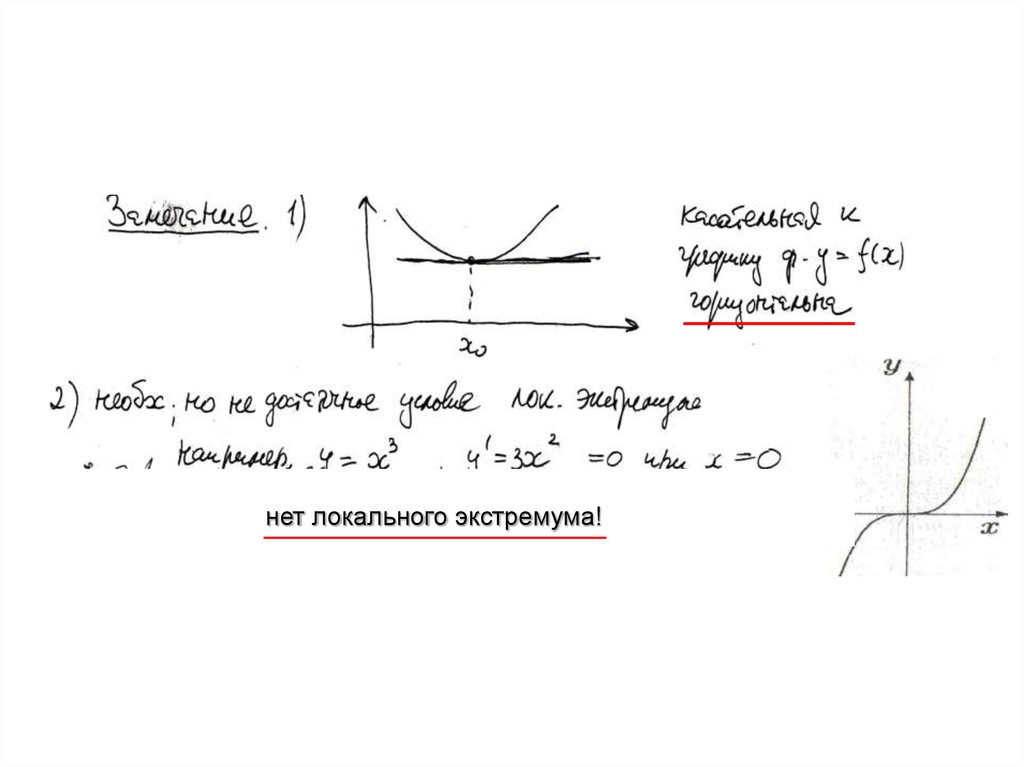
32.
нет локального экстремума!33.
2по 2-й т. Вейерштасса
по т. Ферма
(слайд №)
33
34.
334
35.
435
36.
5Правило Лопиталя-Бернулли
Теорема
)
тогда
х)
36
37.
3738.
3839.
40.
Формула Тейлора (Taylor)Формула Тейлора является одной из жемчужин математического
анализа и широко используется и в теоретических исследованиях, и
вычислительной практике. Эта формула позволяет адекватно
заменить заданную сложным выражением функцию удобным для
анализа многочленом.
______
40
41.
_______________________________________41
42.
4243.
44.
Спасибо за внимание44
45.
Спасибо за внимание45
45
46.
А.С. Монин, Н.Н. КорчагинДесять открытий
в физике океана
Прикладная математика
46и
. открытия в Мировом океане
47.
4747
48.
.48
49.
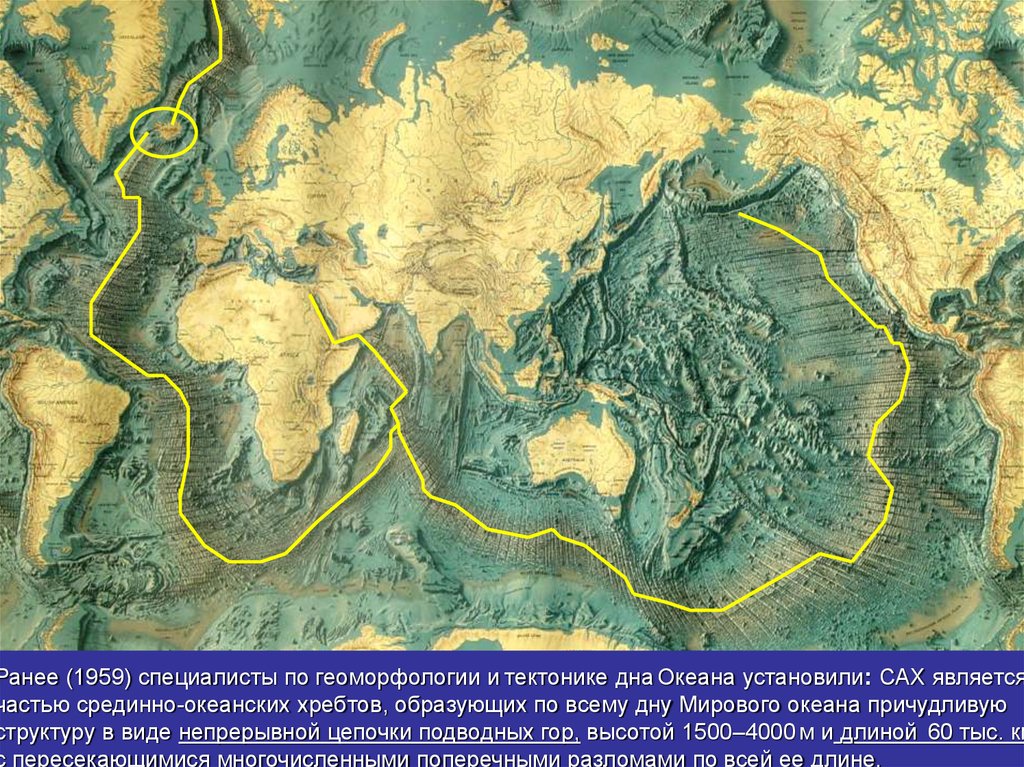
.Ранее (1959) специалисты по геоморфологии и тектонике дна Океана установили: САХ является
частью срединно-океанских хребтов, образующих по всему дну Мирового океана причудливую
49
структуру в виде непрерывной цепочки подводных гор, высотой 1500–4000 м и длиной 60 тыс. км
с пересекающимися многочисленными поперечными разломами по всей ее длине.















































 Математика
Математика








