Взаимное положение прямой и плоскости. Лекция 4

1.

ВЗАИМНОЕ ПОЛОЖЕНИЕ
ПРЯМЫХ И ПЛОСКОСТЕЙ
Горячкина А.Ю.

2.

ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
ТЕОРЕМА. Если прямая параллельна плоскости, то проекции данной
прямой параллельны одноименным проекциям какой-либо прямой,
принадлежащей данной плоскости:
a ║ α < = > a' ║ lα ' ᴧ a'' ║ lα ''
Построить проекции прямой a,
проходящей через точку A и
параллельной плоскости α
2"
a"
A"
f"
l"
h"
B"
1"
x
2'
f'
B'
a'
a ║ α (h, f) , l
A'
l'
1'
h'
α < = > a' ║ l ' ᴧ a'' ║ l ''

3.

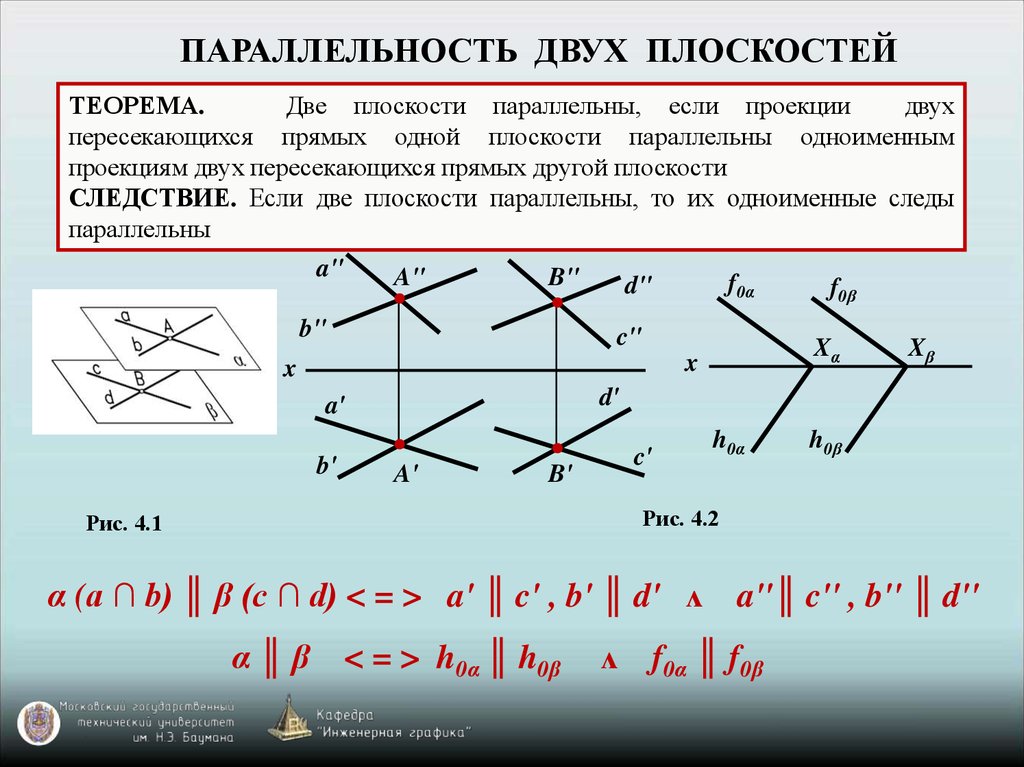
ПАРАЛЛЕЛЬНОСТЬ ДВУХ ПЛОСКОСТЕЙ
ТЕОРЕМА.
Две плоскости параллельны, если проекции
двух
пересекающихся прямых одной плоскости параллельны одноименным
проекциям двух пересекающихся прямых другой плоскости
СЛЕДСТВИЕ. Если две плоскости параллельны, то их одноименные следы
параллельны
a"
A"
B"
b"
f0α
d"
c"
Xα
x
x
Xβ
d'
a'
b'
f0β
A'
B'
c'
h0α
h0β
Рис. 4.2
Рис. 4.1
α (a ∩ b) ║ β (c ∩ d) < = > a' ║ c' , b' ║ d' ᴧ a''║ c'' , b'' ║ d''
α ║ β < = > h0α ║ h0β
ᴧ f0α ║ f0β

4.

ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
В общем случае отношение перпендикулярности в пространстве не сохраняет
признаков перпендикулярности на чертеже
ТЕОРЕМА. Если прямая перпендикулярна плоскости, то горизонтальная проекция
прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а
фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали
данной плоскости
n ┴ α (h, f) < = > n' ┴ h' ᴧ n'' ┴ f ''
Пример: Построить проекции прямой, перпендикулярной к заданной плоскости
и проходящей через точку A.
n"
f"
f0α
n"
h"
A"
x
f'
A'
A"
A'
n'
n'
Рис. 4.3
x
Xα
Рис. 4.4
h'
Рис. 4.5
h0α

5.

ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ
ТЕОРЕМА. Если плоскости взаимно перпендикулярны, то одна из них
содержит хотя бы одну прямую, горизонтальная проекция которой
перпендикулярна
горизонтальной
проекции
горизонтали
(горизонтальному следу) плоскости, а фронтальная проекция прямой
перпендикулярна фронтальной проекции фронтали (фронтальному следу)
данной плоскости
Рис. 4.6

6.

Пример: Построить проекции плоскости, перпендикулярной к заданной
плоскости и проходящей через точку A и прямую a
n"
c"
d"
2"
a"
1"
h"
3"
f"
K"
A"
x
a'
K'
3'
A'
n'
c'
f'
1'
2'
h'
d'
β (а , n) ┴ α (c , d ) < = > n' ┴ h' , n'' ┴ f ''
Рис. 4.7

7.

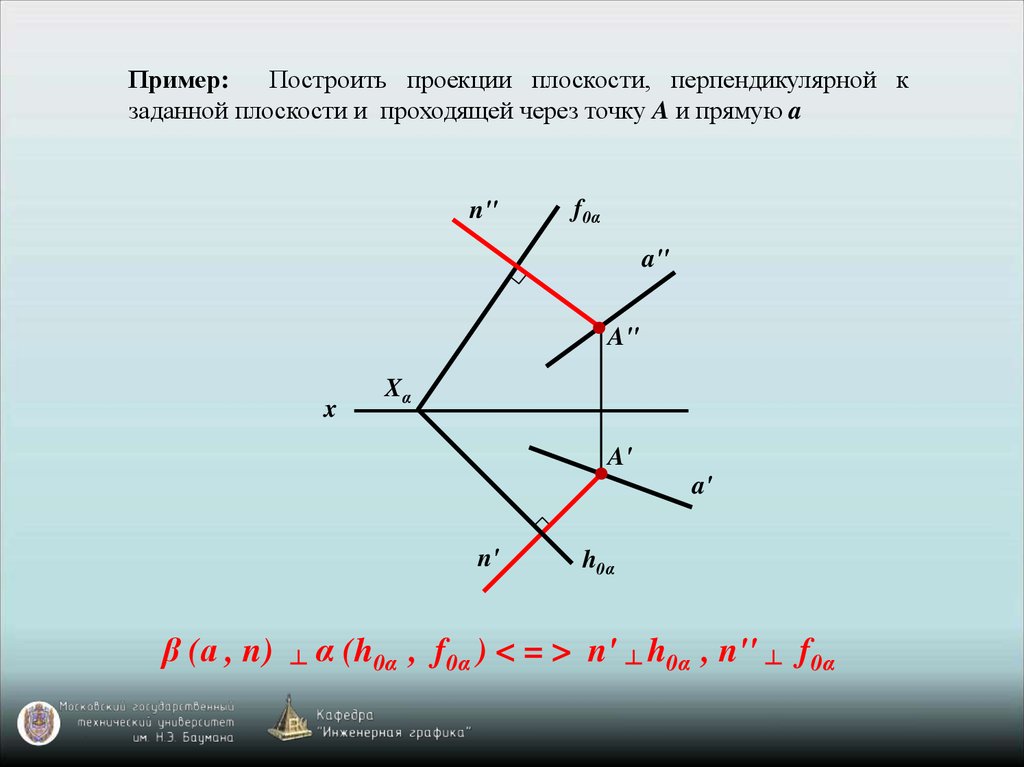
Пример:
Построить проекции плоскости, перпендикулярной к
заданной плоскости и проходящей через точку A и прямую a
n"
f0α
a"
A"
x
Xα
A'
a'
n'
β (а , n)
┴
h0α
α (h0α , f0α ) < = > n' ┴ h0α , n'' ┴ f0α

8.

ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
Пересечение плоскостей, одна из которых проецирующая
Примечание. Одна из проекций искомой линии пересечения известна
сразу: она совпадает с соответствующим следом проецирующей
плоскости.
Вторая проекция находится по принадлежности искомой линии
другой, непроецирующей плоскости
Рис. 4.8

9.

Пересечение плоскостей, одна из которых проецирующая
f0 β
1"
B"
C"
A"
x
2"
Xβ
l"
B'
1'
l'
A'
C'
2'
h0β
Рис. 4.9
α (ABC) ∩ β (β ┴ π1) = > l '
h0β

10.

Пересечение двух плоскостей общего положения
Пример: Построить линии пересечения заданных плоскостей
α ∩ β = K1K2
Алгоритм решения:
K1
K2
Рис. 4.11
1
2
1. Ввести плоскость-посредник γ1 (γ1 ┴ π)
2. Построить линии пересечения плоскости
γ1 с каждой из заданных плоскостей:
γ1 ∩ α = n1
γ1 ∩ β = m1
3. Найти точку K1 пересечения
построенных линий
n1 ∩ m1 = K1
4. Ввести вторую плоскость-посредник γ2
(γ2 ┴ π) и повторить построения (п.п. 2,
3) для нахождения точки K2
γ2 ∩ α = n2
γ2 ∩ β = m2
n2 ∩ m2 = K2
5. Провести искомую прямую K1 K2 через
две найденные точки

11.

Пересечение двух плоскостей общего положения
a"
b"
8"
4"
K2"
7"
c"
d"
3"
6"
f0γ2
5"
K1" 2"
f0γ1
1"
x
K1'
3'
4'
2'
K2'
7'
8'
a'
1'
6'
b'
Рис. 4.11
d'
5'
c'

12.

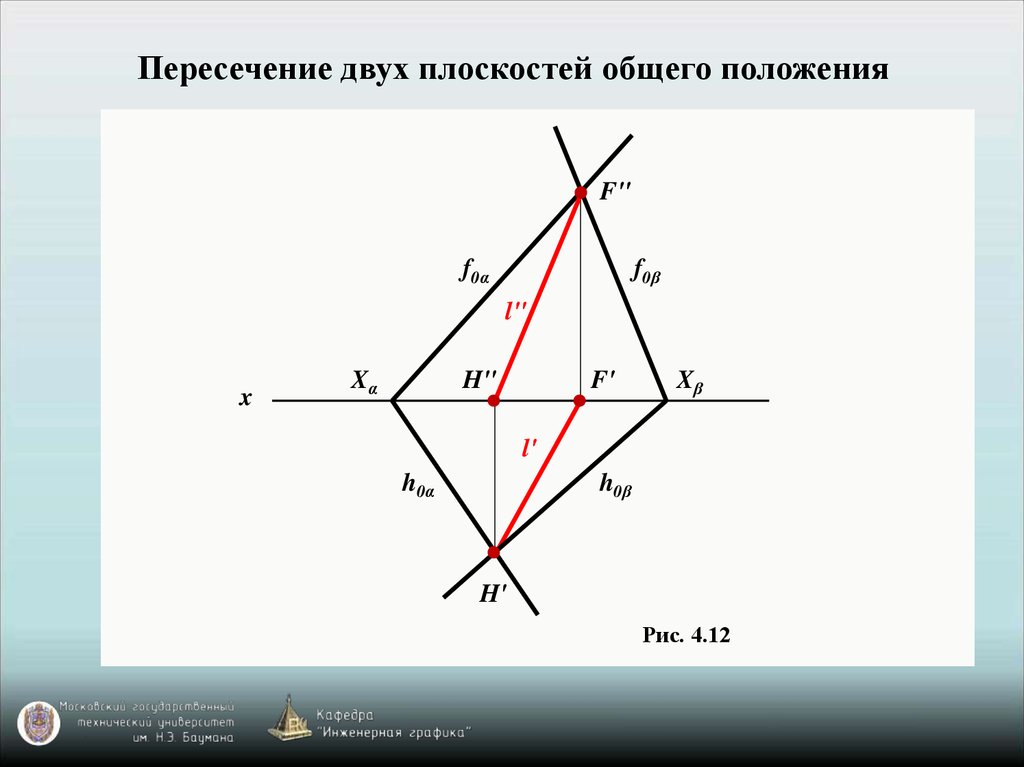
Пересечение двух плоскостей общего положения
F"
f0α
f0β
l"
x
Xα
H"
F'
Xβ
l'
h0α
h0β
H'
Рис. 4.12

13.

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
Одна из поверхностей – проецирующая
1. Пересечение прямой общего положения с проецирующей плоскостью
f0α
K"
a"
x
Xα
a'
K'
Рис. 4.13
Рис. 4.14
h0α
α ∩ а = K , α ┴ π1 = > K '
h0α

14.

2. Пересечение проецирующей прямой с плоскостью общего положения
a"
1"
B"
K"
2"
A"
C"
3"
B'
1'
a' ≡K'
A'
3'
Рис. 4.15
2'
C'
α (ABC) ∩ а = K , а ┴ π1
= > K' а'
Рис. 4.16

15.

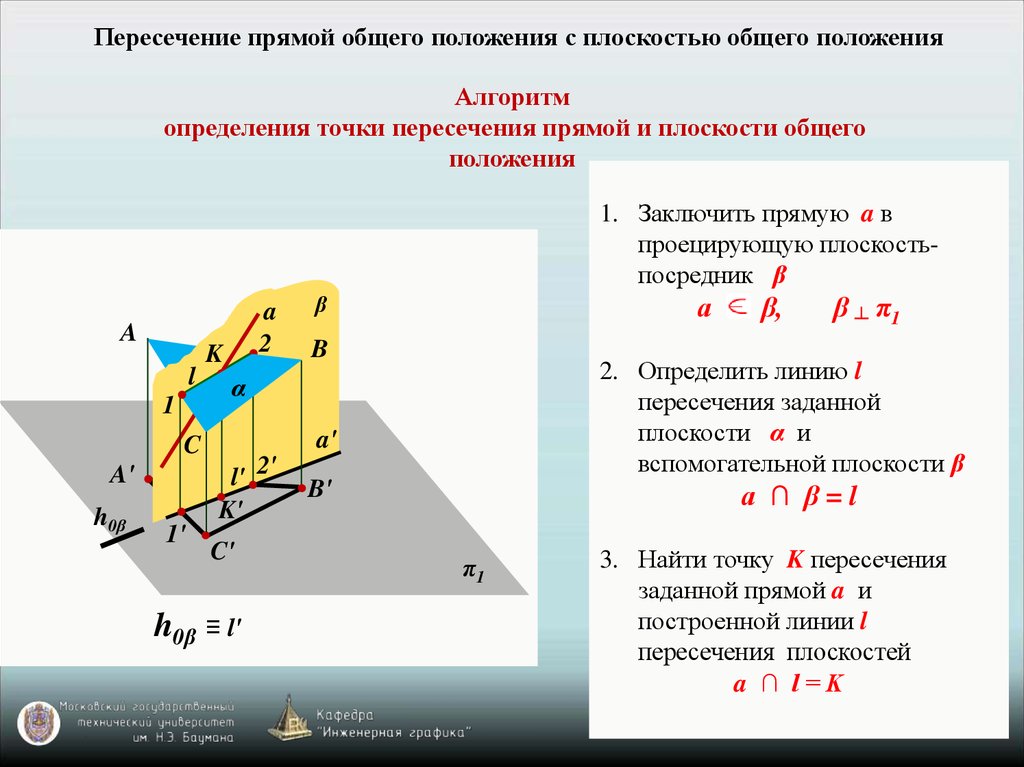
Пересечение прямой общего положения с плоскостью общего положения
Алгоритм
определения точки пересечения прямой и плоскости общего
положения
1. Заключить прямую a в
проецирующую плоскостьпосредник β
A
l
1
C
A'
h0β
1'
a
2
K
а
β
B
a'
C'
h0β ≡ l'
β ┴ π1
2. Определить линию l
пересечения заданной
плоскости α и
вспомогательной плоскости β
α
l' 2'
K'
β,
B'
a ∩ β=l
π1
3. Найти точку K пересечения
заданной прямой a и
построенной линии l
пересечения плоскостей
a ∩ l=K

16.

Задача. Построить проекции точки пересечения прямой а с
плоскостью, заданной пересекающимися прямыми b и c
1.
а
a"
1"
4" 5"≡6"
β, β ┴ π1
2. a ∩ β = l
K"
A"
3. a ∩ l = K
b"
l"
3"
2"
c"
x
a'
1, 3 – конкурирующие точки
2, 4
5, 6
c'
2'≡4'
5'
6'
A'
K'
b'
1'≡3'
l'
h0β
Рис. 4.18