Похожие презентации:
Случайные события. (Лекция 2)
1. Случайные события
1. Классификация.2. Алгебра событий.
2. 1. Классификация событий
3. Классификация событий
Случайным событием называется такойисход эксперимента или наблюдения,
который
при
реализации
данного
комплекса условий может произойти, а
может и не произойти.
A, B, C…
16.05.16
Ирина Юрьевна Хар
4. Классификация событий
Достоверным событием называется такоесобытие, которое при реализации данного
комплекса условий непременно произойдет.
U
16.05.16
Ирина Юрьевна Хар
5. Классификация событий
Невозможным событием называется такоесобытие, которое заведомо не может
произойти при реализации данного комплекса
условий.
V
16.05.16
Ирина Юрьевна Хар
6. Классификация событий
События А и В называютсянесовместными, если в результате
данного испытания появление одного
из них исключает появление второго.
16.05.16
Ирина Юрьевна Хар
7. Классификация событий
События А и В называютсясовместными, если в результате
данного испытания появление одного
из них не исключает появление
второго.
16.05.16
Ирина Юрьевна Хар
8. Классификация событий
Два события А и А называютсяпротивоположными, если не появление
одного из них влечет появление другого.
16.05.16
Ирина Юрьевна Хар
9. Классификация событий
Двасобытия
называются
независимыми, если осуществление
одного не влияет на возможность
осуществления другого.
16.05.16
Ирина Юрьевна Хар
10. Классификация событий
Два события называются зависимыми,если осуществление одного влияет на
возможность осуществления другого.
16.05.16
Ирина Юрьевна Хар
11. Классификация событий
Пусть производится одинвыстрел по мишени
16.05.16
Ирина Юрьевна Хар
12. Классификация событий
Ai — "выбито i очков, где i изменяется от 0 до 10",В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".
16.05.16
Ирина Юрьевна Хар
13. Классификация событий
Ai — "выбито i очков, где i изменяется от 0 до 10",В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".
несовместные
16.05.16
В и С,
А6 и F,
А3 и В
Ирина Юрьевна Хар
14. Классификация событий
Ai — "выбито i очков, где i изменяется от 0 до 10",В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".
совместные
16.05.16
А8 и В,
А3 и С,
А2 и F,
А5 и H
Ирина Юрьевна Хар
15. Классификация событий
Ai — "выбито i очков, где i изменяется от 0 до 10",В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".
противоположные
16.05.16
В и С,
D иF
Ирина Юрьевна Хар
16. Классификация событий
Ai — "выбито i очков, где i изменяется от 0 до 10",В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".
невозможное
16.05.16
G
Ирина Юрьевна Хар
17. Классификация событий
Ai — "выбито i очков, где i изменяется от 0 до 10",В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".
достоверное
16.05.16
H
Ирина Юрьевна Хар
18. Классификация событий
Событие А называется благоприятствующимсобытию В,
если появление события А влечет за собой
появление события В.
А В или А В
16.05.16
Ирина Юрьевна Хар
19. Классификация событий
Ai — "выбито i очков, где i изменяется от 0 до 10",В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".
А1,
А2,
А3,
А4
16.05.16
F
Ирина Юрьевна Хар
20. Классификация событий
Ai — "выбито i очков, где i изменяется от 0 до 10",В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".
А1,
А3,
А5,
А7,
16.05.16 A9
F
Ирина Юрьевна Хар
21. Классификация событий
События А и В называются равносильными, еслипоявление события А влечет за собой появление
события В и в то же время появление события В
влечет за собой появление события А.
А В или А=В
16.05.16
Ирина Юрьевна Хар
22. Классификация событий
Ai — "выбито i очков, где i изменяется от 0 до 10",В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".
D
16.05.16
F
Ирина Юрьевна Хар
23. Классификация событий
Ai — "выбито i очков, где i изменяется от 0 до 10",В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".
1. А0, А1, A2, A3, A4, A5, A6, A7, A8, A9, A10
2. В и С;
3. D и F.
16.05.16
Ирина Юрьевна Хар
24. Классификация событий
Если группа событий такова, что в результатеиспытания обязательно должно произойти
хотя бы одно из них, то эта группа событий
называется полной группой событий.
16.05.16
Ирина Юрьевна Хар
25. Классификация событий
Ai — "выбито i очков, где i изменяется от 0 до 10",В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".
1. А0, А1, A2, A3, A4, A5, A6, A7, A8, A9, A10
2. В и С;
3. D и F.
16.05.16
Ирина Юрьевна Хар
26. Классификация событий
Каждое событие из полной группы попарнонесовместных событий будем называть исходом
данного опыта (испытания). Часто исходы испытания
называются элементарными событиями.
Множество всех возможных элементарных событий
данного опыта называется пространством
элементарных событий Е, а сами элементарные
события еi — точками этого пространства.
16.05.16
Ирина Юрьевна Хар
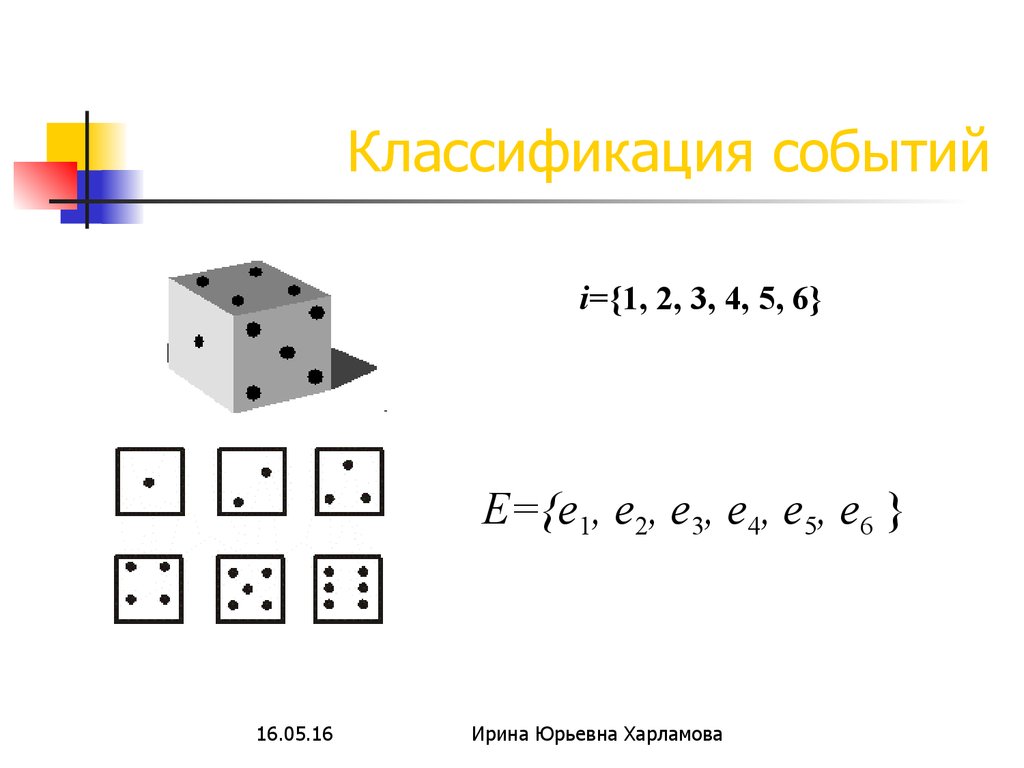
27. Классификация событий
i={1, 2, 3, 4, 5, 6}E={е1, е2, е3, е4, е5, е6 }
16.05.16
Ирина Юрьевна Харламова
28. Случайные события
1 2 3 4 5 61
2
3
4
5
6
1,1 1,2 1,3 1,4 1,5 1,6
2,1 2,2 2,3 2,4 2,5 2,6
3,1 3,2 3,3 3,4 3,5 3,6
4,1 4,2 4,3 4,4 4,5 4,6
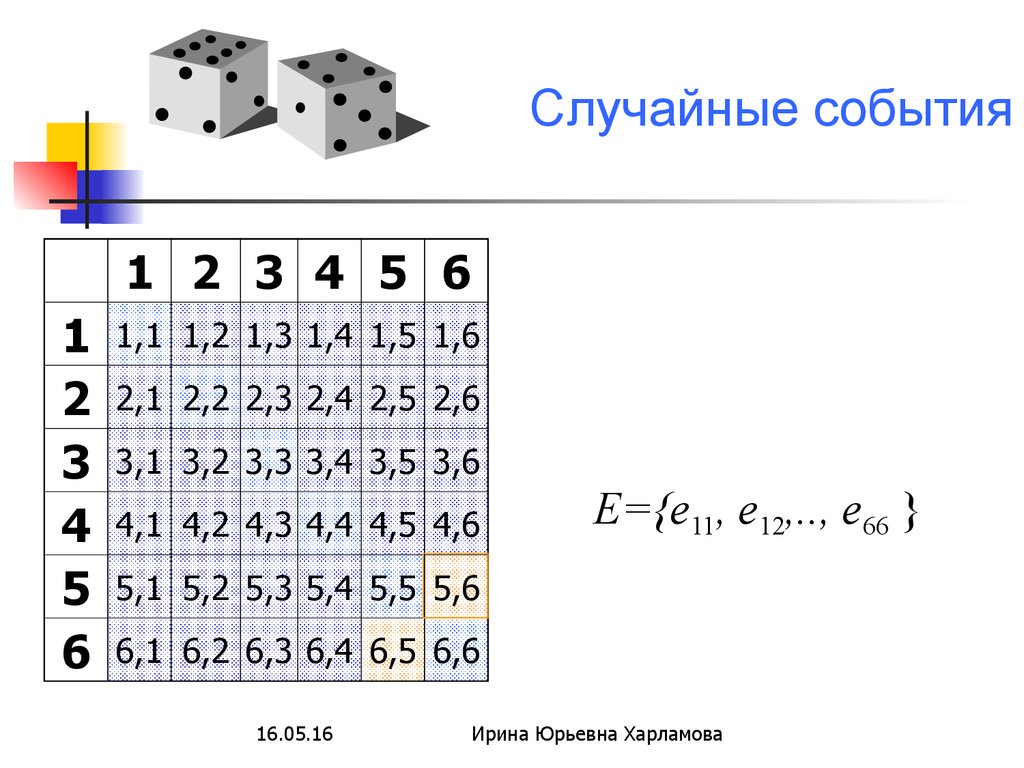
E={е11, е12,.., е66 }
5,1 5,2 5,3 5,4 5,5 5,6
6,1 6,2 6,3 6,4 6,5 6,6
16.05.16
Ирина Юрьевна Харламова
29. Случайные события
16.05.16Ирина Юрьевна Харламова
30. Классификация событий
События называютсяравновозможными, если по условию
испытания нет основания считать какое
либо из них более возможным, чем
другое.
16.05.16
Ирина Юрьевна Харламова
31. 2. Алгебра случайных событий
32. Алгебра событий
Суммой (объединением) двух событий Аи В называется третье событие С,
состоящее в появлении или события А,
или события В, или обоих этих
событий.
C A B
16.05.16
C A B
Ирина Юрьевна Харламова
33. Алгебра событий
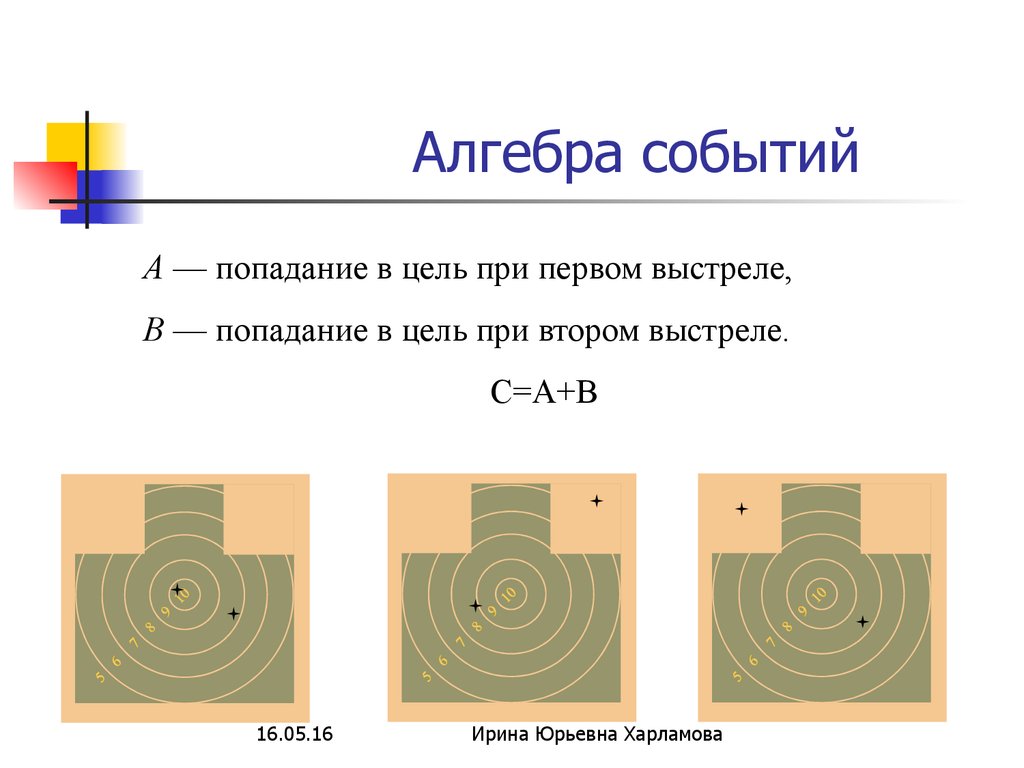
А — попадание в цель при первом выстреле,В — попадание в цель при втором выстреле.
С=A+B
16.05.16
Ирина Юрьевна Харламова
34. Алгебра событий
Суммой (объединением) несколькихсобытий А1, А2 ,..., Аn называется событие
А=А1+ А2+...+Аn,
состоящее в появлении хотя бы одного из
этих событий.
16.05.16
Ирина Юрьевна Харламова
35. СУММА
A16.05.16
B
Ирина Юрьевна Харламова
36. Алгебра событий
Произведением (пересечением) двухсобытий А и В называется такое третье
событие С, которое состоит в
совместном появлении и события А, и
события В.
C A B
16.05.16
C A B
Ирина Юрьевна Харламова
37. Алгебра событий
А — попадание в цель при первом выстреле,В — попадание в цель при втором выстреле.
С=A·B
16.05.16
Ирина Юрьевна Харламова
38. Алгебра событий
Произведением (объединением) несколькихсобытий А1, А2 ,..., Аn называется событие
А=А1· А2·...·Аn,
состоящее в состоящее в совместном
появлении всех этих событий.
16.05.16
Ирина Юрьевна Харламова
39. ПРОИЗВЕДЕНИЕ
16.05.16Ирина Юрьевна Харламова
40. Алгебра событий
Если события А1 и А2 — несовместныесобытия, то их произведение —
невозможное событие.
A1 A2 V
16.05.16
Ирина Юрьевна Харламова
41. Алгебра событий
1. Произведение противоположныхсобытий — невозможное событие:
A A V.
2. Сумма противоположных событий —
достоверное событие. :
16.05.16
A A U.
Ирина Юрьевна Харламова






































 Математика
Математика Философия
Философия








