Похожие презентации:
Парная линейная регрессия
1. ПАРНАЯ РЕГРЕССИЯ
2.
Регрессия – зависимость между независимыми(объясняющими) переменными и условным
математическим ожиданием зависимой (объясняемой)
переменной
f ( x) M (Y / X )
Парная регрессия -- регрессия между двумя переменными
y f (a, x)
yi yˆ xi i
y иx
3.
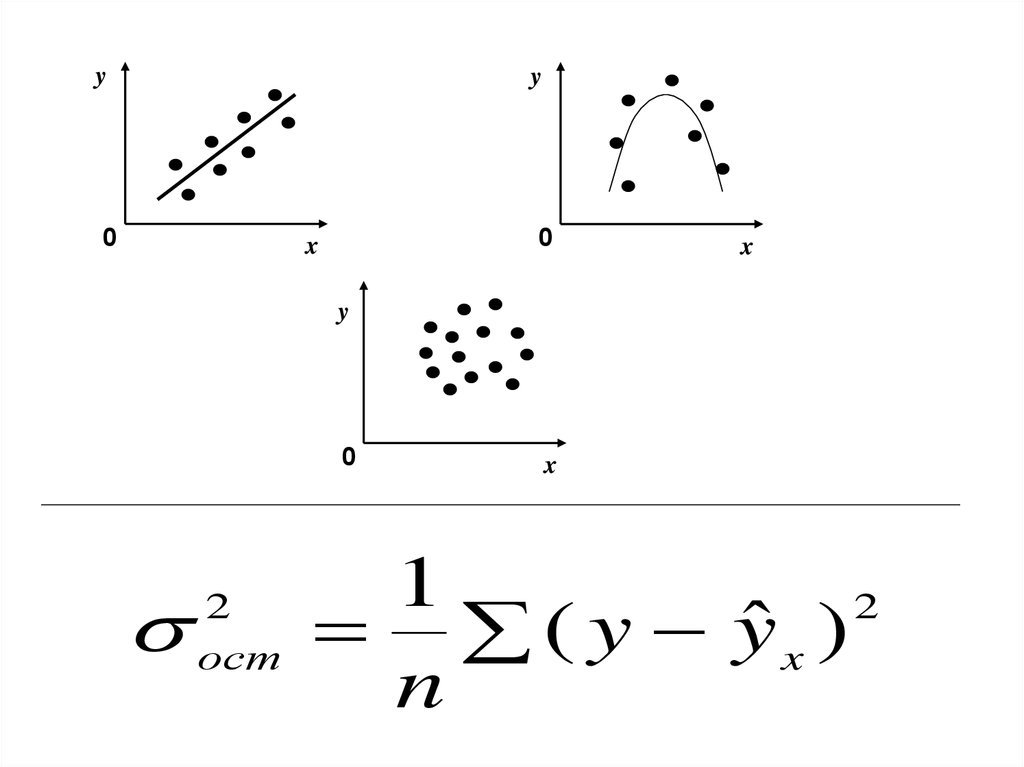
yy
0
0
x
x
y
0
2
ост
x
1
2
(y y
ˆx )
n
4.
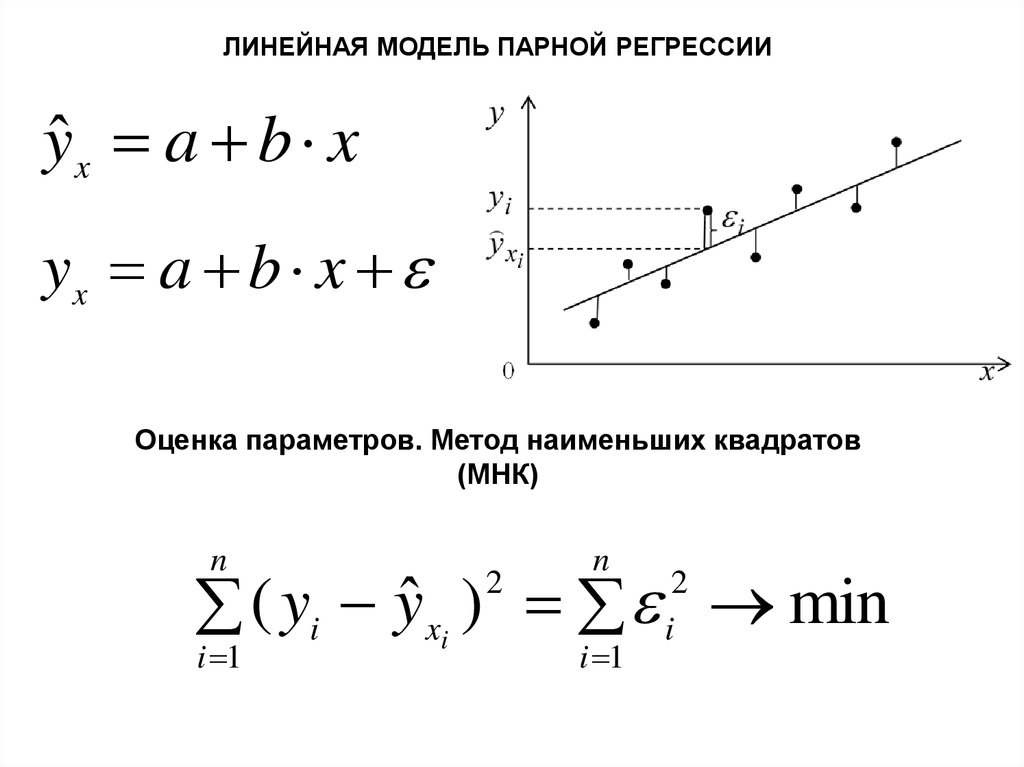
ЛИНЕЙНАЯ МОДЕЛЬ ПАРНОЙ РЕГРЕССИИyˆ x a b x
yx a b x
Оценка параметров. Метод наименьших квадратов
(МНК)
n
n
( yi yˆ x ) min
i 1
2
i
i 1
2
i
5.
Оценка параметров. МНКОбозначим
2
i
через
S a, b
i
,
S a, b y a b x
S
a 2 y a b x 0;
S 2 x y a b x 0.
b
a n b x y;
2
a
x
b
x
x y.
2
6.
Оценка параметров. МНКb
cov x, y
a y b x
2
x
______
cov x, y y x y x
1
x x
n
1
y y
n
______
____
2
x x
2
x
1
y x y x
n
____
1
2
2
x x
n
2
7.
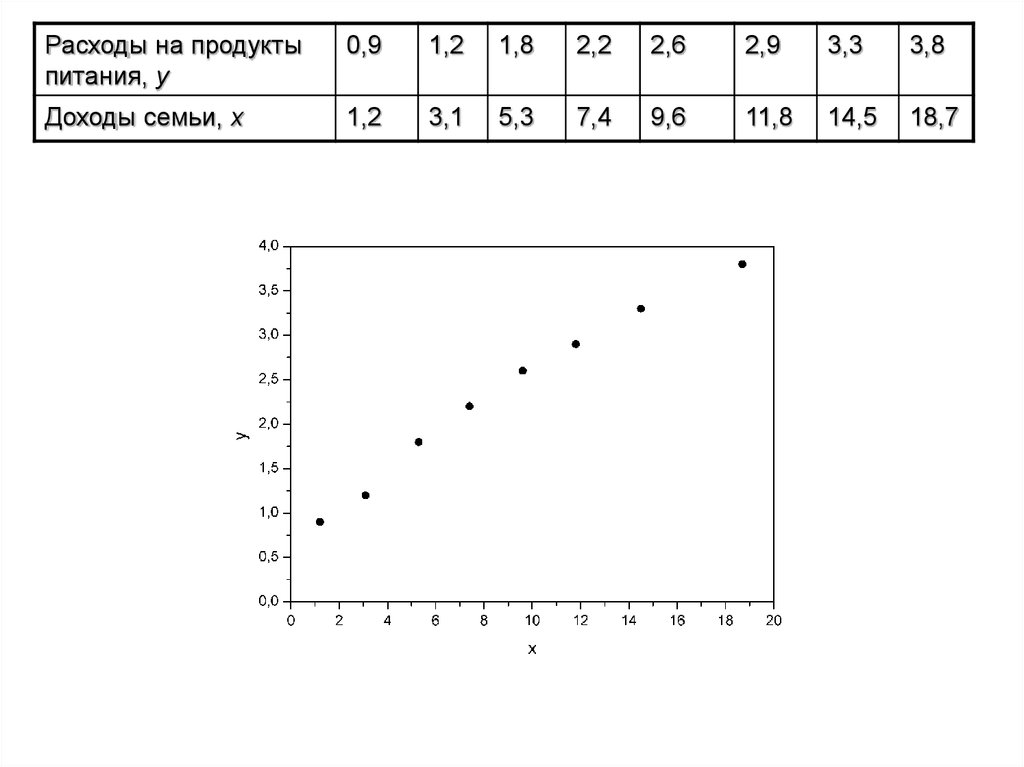
Расходы на продуктыпитания, y
0,9
1,2
1,8
2,2
2,6
2,9
3,3
3,8
Доходы семьи, x
1,2
3,1
5,3
7,4
9,6
11,8
14,5
18,7
8.
yx
x y
x
2
y
2
1
2
3
4
5
6
1
1,2
0,9
1,08
1,44
0,81
2
3,1
1,2
3,72
9,61
1,44
3
5,3
1,8
9,54
28,09
3,24
4
7,4
2,2
16,28
54,76
4,84
5
9,6
2,6
24,96
92,16
6,76
6
11,8
2,9
34,22
139,24
8,41
7
14,5
3,3
47,85
210,25
10,89
8
18,7
3,8
71,06
349,69
14,44
Итого
71,6
18,7
208,71
885,24
50,83
Среднее значение
8,95
2,34
26,09
110,66
6,35
5,53
0,935
–
–
–
30,56
0,874
–
–
–
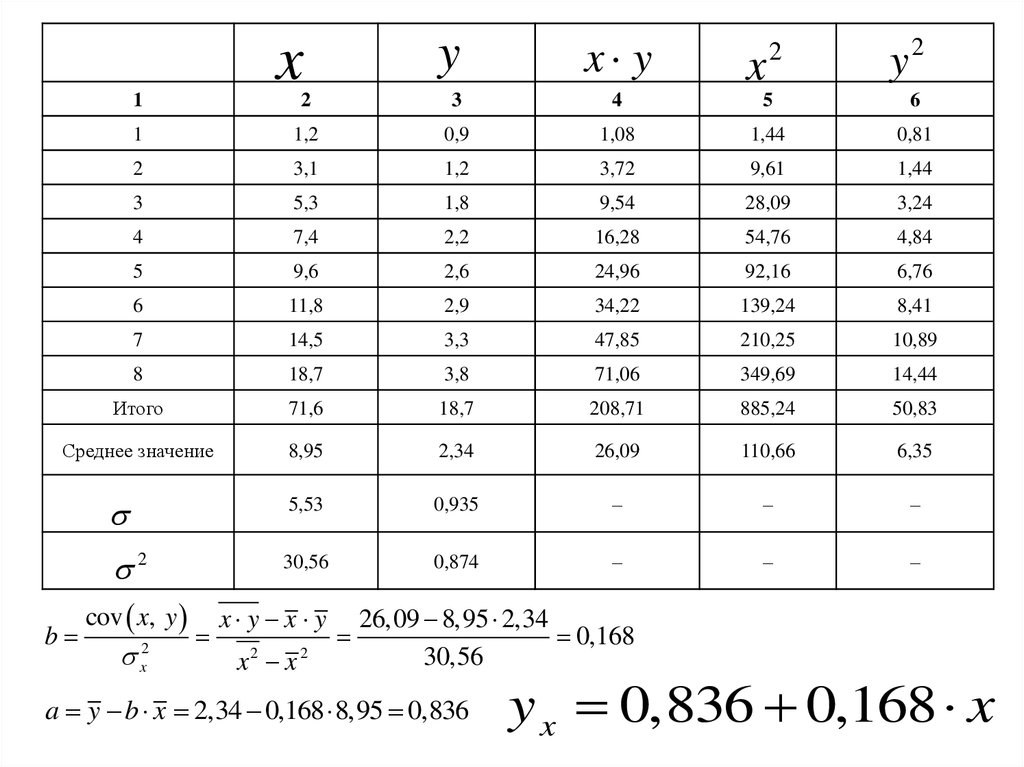
b
2
cov x, y
x2
x y x y
x2 x 2
26,09 8,95 2,34
0,168
30,56
a y b x 2,34 0,168 8,95 0,836
y x 0,836 0,168 x
9.
Исследование уравнения регрессииx cov x, y
rxy b
y
x y
2
rxy 1
2
ост
2
y
1 rxy 1
2
ост
1
y yx
n
2
1
2
2
2
y y y y
n
2
y
10.
Оценка качества модели из относительных отклонениях покаждому наблюдению
y yx
1
A
100%
n
y
11.
Оценка значимости моделиСхема дисперсионного анализа
y y y
2
Компоненты
дисперсии
Сумма квадратов
y y
Общая
y
Факторная
x
Остаточная
F
S
y
2
факт
2
ост
S
y
y y
2
2
2
x
Число степеней
свободы
n 1
2
y y
x
x
2
m
n m 1
Дисперсия на одну
степень свободы
2
Sобщ
S
S
2
факт
2
ост
y y
n 1
y
x
y
m
y y
x
2
2
2
n m 1
k1 m
Fтабл ; k1 ; k2
k2 n m 1
12.
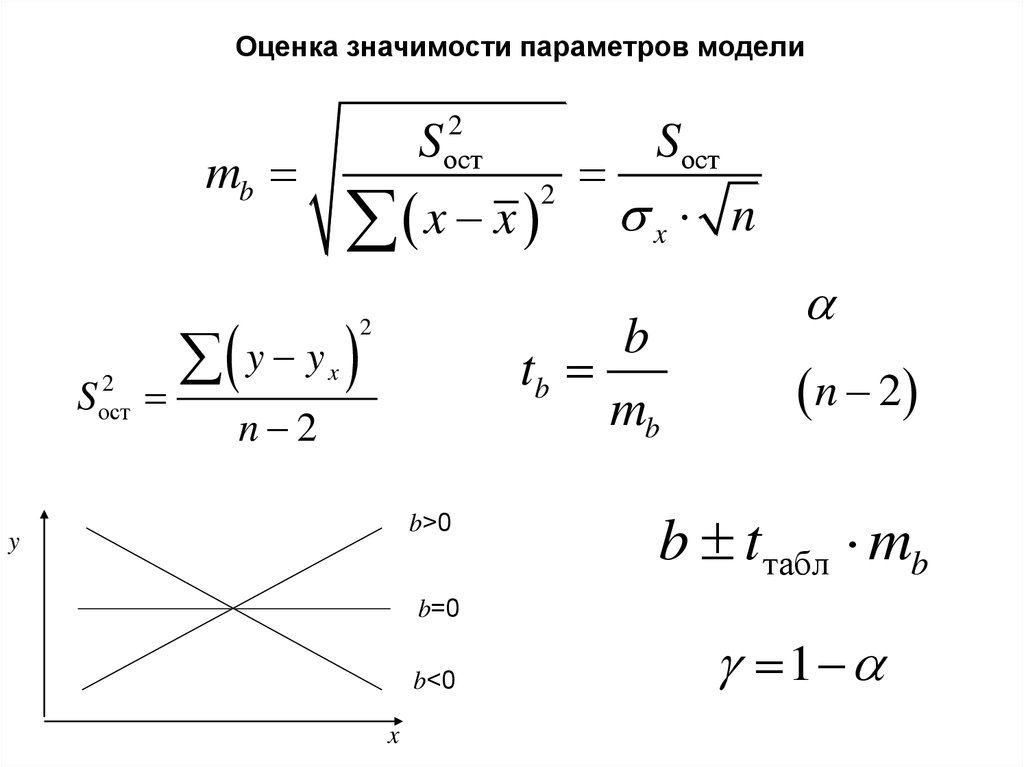
Оценка значимости параметров моделиmb
S
2
ост
y yx
S
2
ост
x x
2
Sост
x n
b
tb
mb
2
n 2
b>0
y
n 2
b tтабл mb
b=0
b<0
x
1
13.
Оценка значимости параметров моделиx
n x x
2
ma S
2
ост
a
ta
ma
a t табл ma
2
Sост
2
x
x n
n 2
1
14.
Построение интервальных оценок дляуравнения парной регрессии
yˆi tтабл m yˆi
m yˆ i
1 ( xi x )
Sост 1
2
n
n x
2
15.
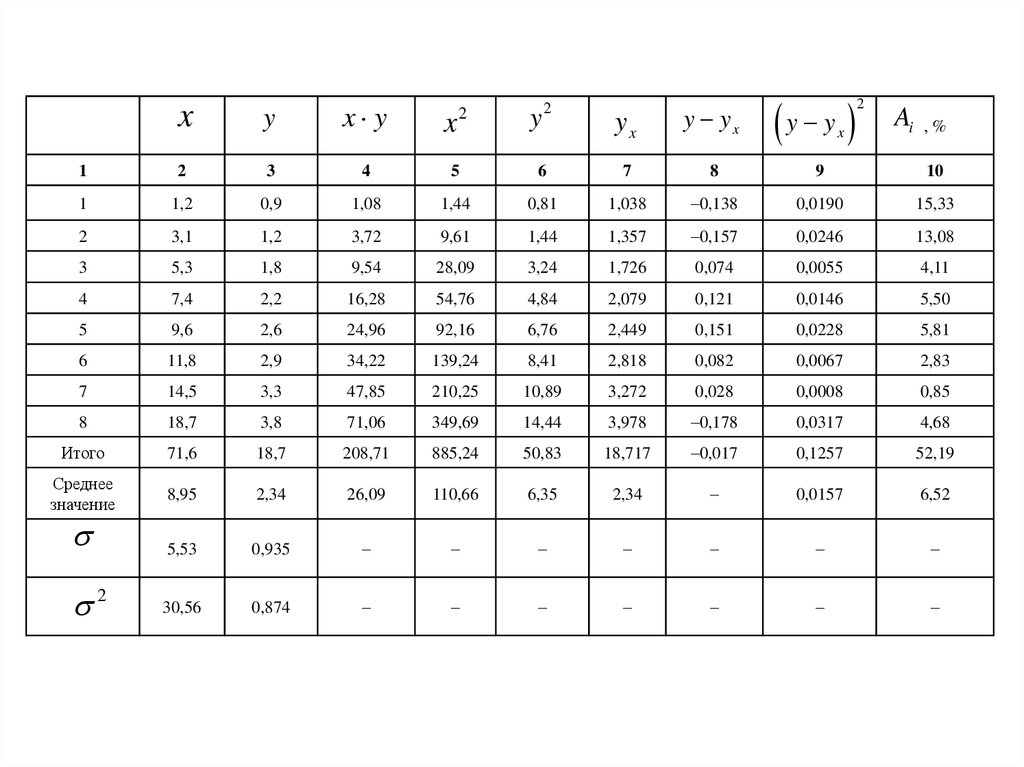
yxy yx
y y
6
7
8
9
10
1,44
0,81
1,038
–0,138
0,0190
15,33
3,72
9,61
1,44
1,357
–0,157
0,0246
13,08
1,8
9,54
28,09
3,24
1,726
0,074
0,0055
4,11
7,4
2,2
16,28
54,76
4,84
2,079
0,121
0,0146
5,50
5
9,6
2,6
24,96
92,16
6,76
2,449
0,151
0,0228
5,81
6
11,8
2,9
34,22
139,24
8,41
2,818
0,082
0,0067
2,83
7
14,5
3,3
47,85
210,25
10,89
3,272
0,028
0,0008
0,85
8
18,7
3,8
71,06
349,69
14,44
3,978
–0,178
0,0317
4,68
Итого
71,6
18,7
208,71
885,24
50,83
18,717
–0,017
0,1257
52,19
Среднее
значение
8,95
2,34
26,09
110,66
6,35
2,34
–
0,0157
6,52
5,53
0,935
–
–
–
–
–
–
–
2
30,56
0,874
–
–
–
–
–
–
–
x
y
x y
x
1
2
3
4
5
1
1,2
0,9
1,08
2
3,1
1,2
3
5,3
4
2
y2
x
2
Ai
,%
16.
x5,53
rxy b
0,168
0,994
y
0,935
Ai
yi y xi
yi
r 0,987
2
xy
A 6,52%
100%
rxy2
0,987
F
n 2
6 455,54
2
1 rxy
1 0,987
Fтабл 5,99
k1 1
k2 n 2 6
0,05
Fфакт Fтабл
17.
S 2 y yxост
n 2
mb
Sост
x n
2
0,1257
0, 021
8 2
0,021
5,53 8
t табл 1,943
2
x
0,0093
0,168
tb
18,065
0,0093
0,05
n 2 6
0,021 885, 24
ma Sост
0,0975
x n
5,53 8
0,836
ta
8,574
0,0975
18.
x p 1,1 x 1,1 8,95 9,845y p 0,836 0,168 9,845 2, 490
2
x
x
1 p
1 9,845 8,95
my Sост 1
0,021 1
0,154
2
p
8
n
n x
8
30,56
2
y p y y p y p y
p
2,113 y p 2,867
p











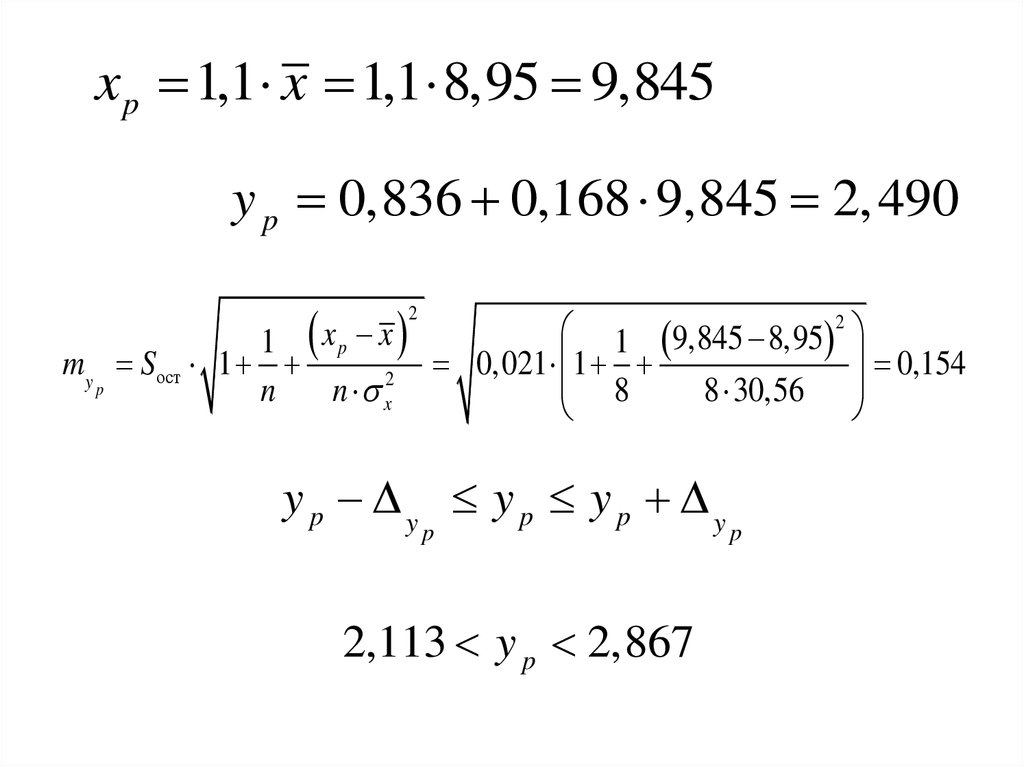
 Математика
Математика








