Похожие презентации:
Решение задач
1.
2.
ОглавлениеЗадача № 1.21 .....………………………………………………………………………… 3
Задача № 1.22 …………………………………………………………………………….
3.
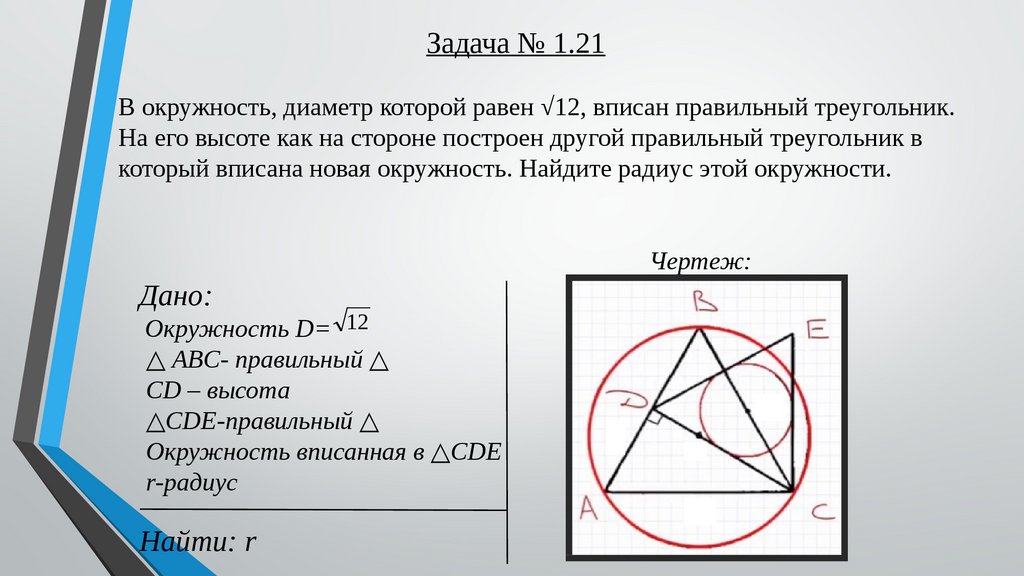
Задача № 1.21В окружность, диаметр которой равен √12, вписан правильный треугольник.
На его высоте как на стороне построен другой правильный треугольник в
который вписана новая окружность. Найдите радиус этой окружности.
Чертеж:
Дано:
Окружность D= 12
△ ABC- правильный △
CD – высота
△CDE-правильный △
Окружность вписанная в △CDE
r-радиус
Найти: r
4.
Решение:R
12
2
△ ABC : AB= R 3
12
3 3
2
CD BC 2 BD 2 32 1,52 1,5 3
Радиус r вписанной окружности :
a 3 1,5 3 3 3
0,75
r=
6
4
6
Ответ: 0,75
5.
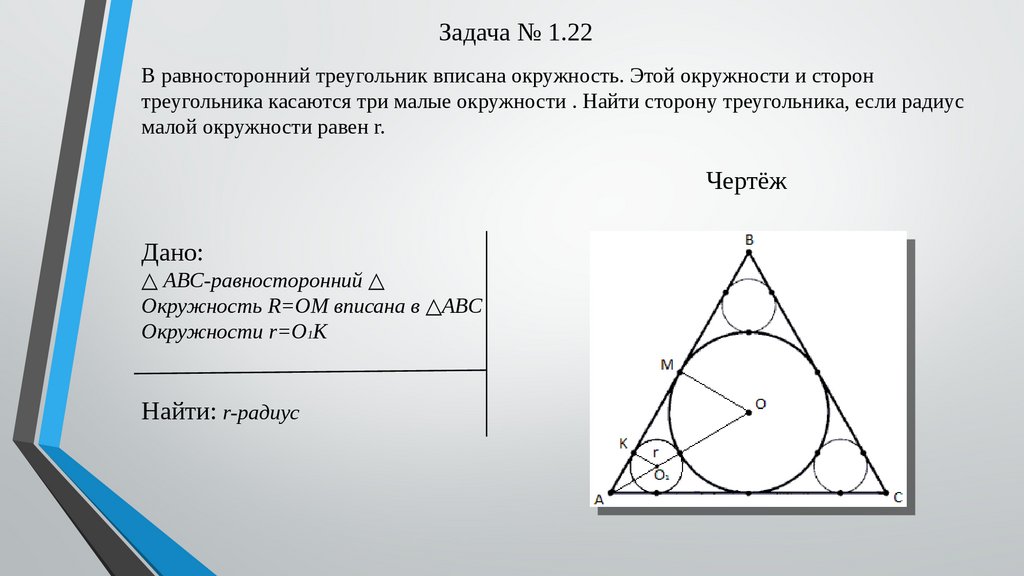
Задача № 1.22В равносторонний треугольник вписана окружность. Этой окружности и сторон
треугольника касаются три малые окружности . Найти сторону треугольника, если радиус
малой окружности равен r.
Чертёж
Дано:
△ ABC-равносторонний △
Окружность R=OM вписана в △ABC
Окружности r=O1K
Найти: r-радиус
6.
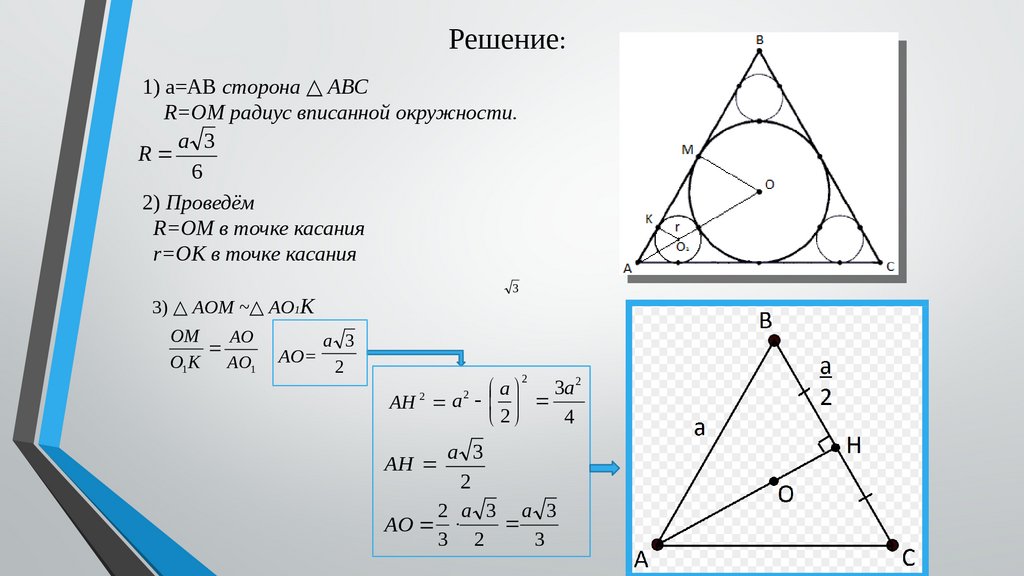
Решение:1) a=AB сторона △ ABC
R=OM радиус вписанной окружности.
a 3
R
6
2) Проведём
R=OM в точке касания
r=ОК в точке касания
3) △ AOM ~△ AO1K
OM
AO
a 3
AO=
O1 K AO1
2
3
2
3a 2
a
2
2
AH a
4
2
a 3
2
2 a 3 a 3
AO
3 2
3
AH
7.
RAO
r AO R r
6 r a 3
9 r
a 3
a 3
6 r
a 3 a 3
3
r
6
3
a 3
3r
2
a 3
2
a 3
9 r
2
a 3 18 r
18 r 3 18 r 3
6 r 3
a 3 3
3
Ответ: 6 r 3
8.
Задача №1.23Стороны треугольника равны 13, 14 и 15 см. Найти отношение площадей описанного
и вписанного в треугольник кругов.
Чертёж:
Дано:
△ ABC
a=AB=13 см
b=BC=14 см
c=AC=15 см
r- радиус вписанной окружности
R- радиус описанной окружности
Найти: Sокр. R
Sокр. r
a
b
c
9.
S1) r= -площадь△
p - полупериметр
R=
Решение:
abc
4S
2) S△= p( p a)( p b)( p c) -формула Герона
S△= 21 8 7 6 7 3 2 4 7 2 3 7 2 2 2 32 4 7 2 3 2 84
p=
13 14 15 42
21
2
2
S 84
3) r= 4
p 21
R
abc 13 14 15 65
8
4
84
4S
SR
R 2 65 2 65 2
4)
S r r 2 8 4 32
65
Ответ:
32
2
10.
Задача № 1.52Около круга радиуса 3 описан равнобедренный треугольник с острым углом 30° при основании.
Определить стороны треугольника.
Дано:
△ ABC- равнобедренный
∠A= ∠C=30°
r =3 радиус вписанной окружности
Найти: стороны треугольника ABC
AB1,BC1,AC
11.
Решение:1) r = OE⊥ BC
∠ABC=180° - (30°+30°)= 120°
BD- высота, медиана, биссектриса.
△BOE : ∠OBE= 60°
∠OEB= 90°
1
∠BOE=30° ⇒ BE= BO (катет лежащий против ∠30°)
2
2) Из △BEO : BO²= OE²+BE²
BO
2
3
BO²=
2
2
BO 2
BO² 9
4
3
BO 2 9
4
4
BO 2 9
3
BO
36
6 3
6 3
2
3
3
3 3
3
12.
Из △ADB : AB= 2 BD (катет лежащий против ∠30°)BD= BO+OD= 2 3 3 ⇒ AB= 2 2 3 3 4 3 6
⇒ AB=BC= 4 3 6
1
4) AC= 2DC = 2EC = 2(BC-BE)= 2 4 3 6 2 3 2 3 3 6 6 3 12
2
△OEC= △ODC
E
r
O
r
C
D
OE=OD=r
OC- общая
EC=DC
по III признаку
равенства треугольников
5)AC= 6 3 12
Ответ: 4
3 6
;4
3 6 ; 6 3 12
2(BC-BE)=
1
1
BO 2 3 3
2
2



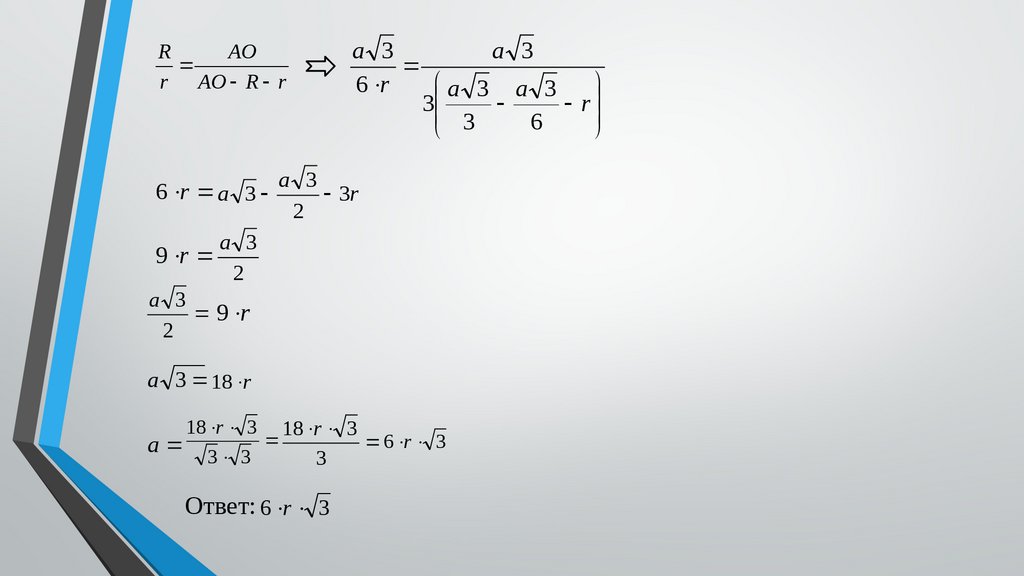





 Математика
Математика








