Элементы специальной теории относительности (СТО). Релятивистская кинематика

1.

2.

.
1. Преобразование Галилея. Механический принцип
относительности
r
т
r'
r r ' R r ' Vt
Y¢
Y
(*)
или
x x' Vx t '
R
O¢
X
O
K
X¢
K¢
Z¢
Z
К – условно неподвижная ИСО
К ’– движущаяся со скоростью
(*)
и
(**)
V const
y y ' V y t '
z z' Vzt '
t t'
относительно К СО
- преобразование Галилея
(**)

3.

d
dt
(*)
' V
F mа
F ' mа '
d
dt
а а'
Ускорение материальной точки во
всех инерциальных системах отсчета
одно и то же!!!
Принцип относительности (ПО) Галилея (механический
ПО) гласит:
во всех инерциальных системах отсчета законы механики
формулируются одинаково, др. словами уравнения,
выражающие законы механики инвариантны по отношению ко
всем ИСО.
Принцип относительности утверждает равноправие
всех инерциальных систем отсчета.

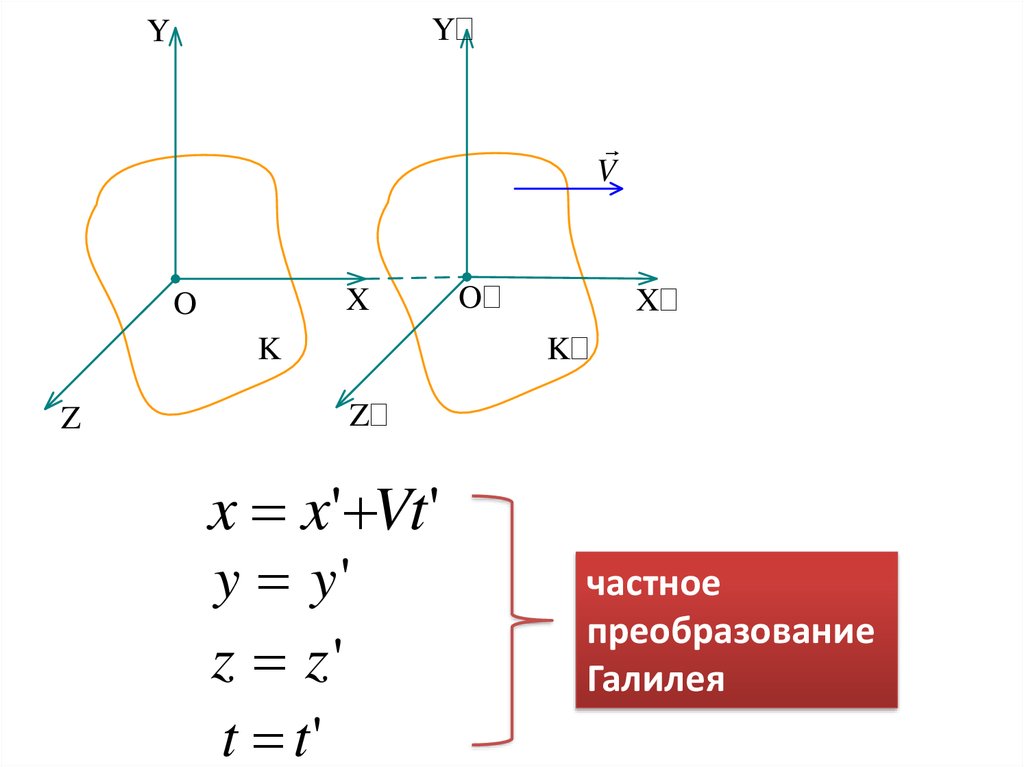
4.

Y¢
Y
V
X
O
K
Z
O¢
X¢
K¢
Z¢
x x' Vt'
y y'
z z'
t t'
частное
преобразование
Галилея

5.

2. Постулаты СТО. (Постулаты Эйнштейна)
- описание любого физического
события или явления зависит от
системы отсчета, в которой
находится наблюдатель
- но, в то время как описание
событий зависит от
наблюдателя, законы природы
от него не зависят, то есть, как
принято говорить на научном
языке, являются
инвариантными
1. Все законы природы во всех инерциальных
системах отсчета имеют один и тот же вид
2. Скорость света в вакууме во всех ИСО одна и та же
5

6.

3. Преобразование Лоренца
K K
V
2 x
t
x Vt
c
x
; y y ; z z ; t
2
2
V
V
1 2
1 2
c
c
Выводы:
-при
V c
знаменатели выражений преобразования
становятся мнимыми и преобразование теряет смысл.
-в нерелятивистском пределе VV
cc
переходит в частное преобразование Галилея.

7.

4. Следствия преобразования Лоренца. Сокращение длин.
V2
l l0 1 2
c
Формула описывает сокращение движущихся предметов (тел) в направлении
движения (лоренцево сокращение).
5 . Замедление хода движущихся часов
t
t
V2
1 2
c
6 . Закон сложения скоростей
V2
V2
'y 1 2
'z 1 2
' x V
c ,
c
x
, y
z
V ' x
V ' x
V ' x
1 2
1 2
1 2
c
c
c

8.

9.

.
1. Необходимость переопределения импульса в релятивистской
динамике
В релятивистской механике СТО под массой частицы понимают ту же самую
(как и в нерелятивистской) величину: масса – мера инертности,
неотрицательный параметр частицы, один и тот же во всех ИСО, т.е.
инвариантный относительно преобразования Лоренца.
Однако, уравнение движения частицы в виде
ma F
(*)
в релятивистской области не работает, и в этом нетрудно убедиться:
движение электрона в постоянном
однородном электростатическом
поле
напряженностью E
e 0 0
t 0 Et
me
e
t
Et
me
d
me
e E
dt
E 1МВ/м 106 В/м
t 2 нс 2 10 с
-9
3,52 108 м / с
c!
абсурд!

10.

Другая версия (*):
Если использовать определение
dp
F
dt
(**)
p m :
- получим снова выражение (*);
- можно доказать, что закон сохранения импульса не будет инвариантен при
переходе из одной ИСО к другой.
Нерелятивистское определение импульса надо «переопределить», можно
доказать, что 2-й з-н Ньютона в форме (**) будет инвариантом, если
p
m
1
2
c2
Релятивистский импульс

11.

движение электрона в
постоянном
однородном
электростатическом
поле…
dp
eE
dt
p p0 eEt
p t eEt
me t
1
t
t c
2
c
p0 0
eEt
2
eEt
eEt mec
2
Из последней формулы видно, что при всех конечных
2
t
t c ! ч.т.д.

12.

2. Релятивистская энергия частицы. Связь между энергией и
импульсом. Энергия покоя.
E
mc2
1
2
c
Релятивистский энергия
2
2
E
2
p inv
2
c
2
E
2
2
p
mc
c2
2
E02
(***)
Покоящаяся частица (материальная точка) обладает отличной от нуля
энергией:
E0 mc 2 Энергия покоя

13.

3. Кинетическая энергия частицы
1
2
T E E0 mc
1
2
1 2
c
а затем
если
1
1
2
1
2
8
1
m
T
2
/c
2
2
пренебрегая
членами
высокого
порядка
2
как в классической механике!!

14.

Найдем связь между энергией и импульсом
Итак
E T E0 T mc2
подставим в (***)
E 2 p 2c 2 E02
p c E E
2 2
2
2
0
p c ( E E0 )( E E0 ) T (T 2 E0 ) T (T 2mc )
2 2
2
1
2
p
T (T 2mc )
c
при
T mc2
p 2mT
как в классической механике!!

15.

4. Релятивистская масса частицы. Частицы с нулевой массой.
mr
m
1
2
c
2
p mr
E mr c
2
В природе существуют очень интересные объекты – частицы с нулевой
массой. Примером такой частицы является фотон – квант электромагнитного
излучения. Выражение для релятивистской энергии
E
mc2
1
2
c2
показывает, что она может быть
отличной от нуля при m 0 только в том
случае, если скорость частицы (всегда,
относительно любой инерциальной
системы отсчета!) равна с