Графический способ решения систем уравнений

1. Графический способ решения систем уравнений

2. Цели урока

• Закрепить навыки построения графиков
функций
• Ввести уравнение окружности
• Использовать графический метод для
решения систем уравнений
• Применить графический метод при
решении заданий с параметрами

3.

Повторение
1.Что является графиком уравнения ху=9 ?
гипербола
2. Что является графиком уравнения х+у=9 ?
прямая
2
2
3. Что является графиком уравнения х+у =9 ?
окружность
2
4. Что является графиком уравнения х + у =9
парабола

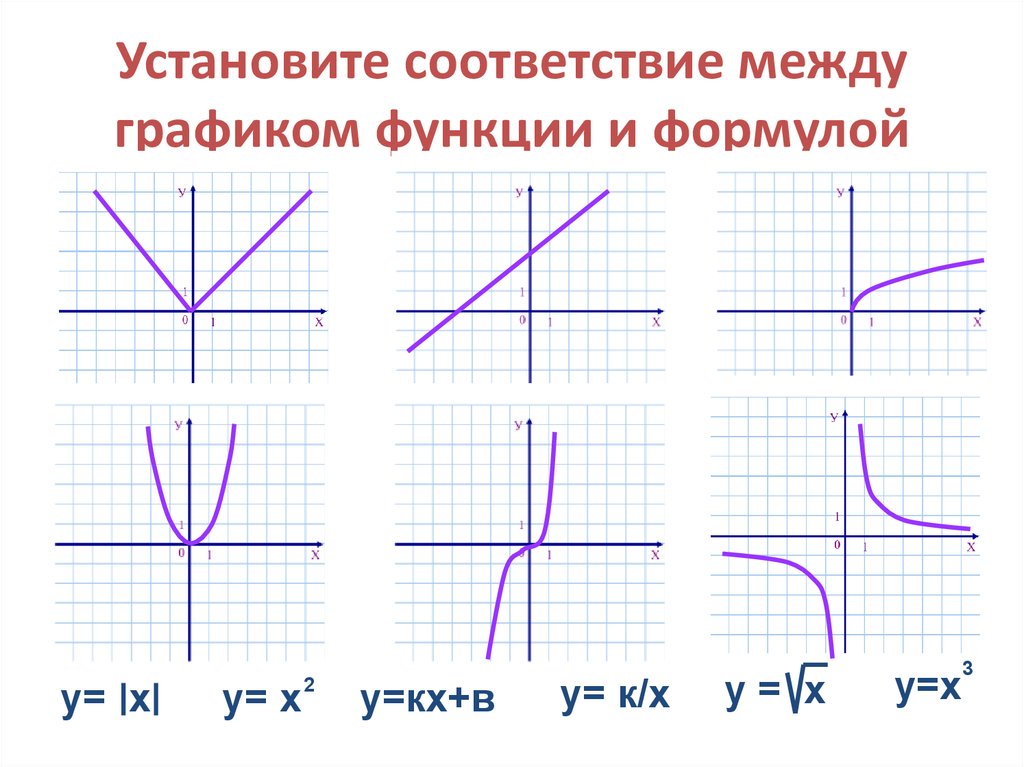
4. Установите соответствие между графиком функции и формулой

у= х
у= х
2
у=кх+в
у= к/х
у= х
3
у=х

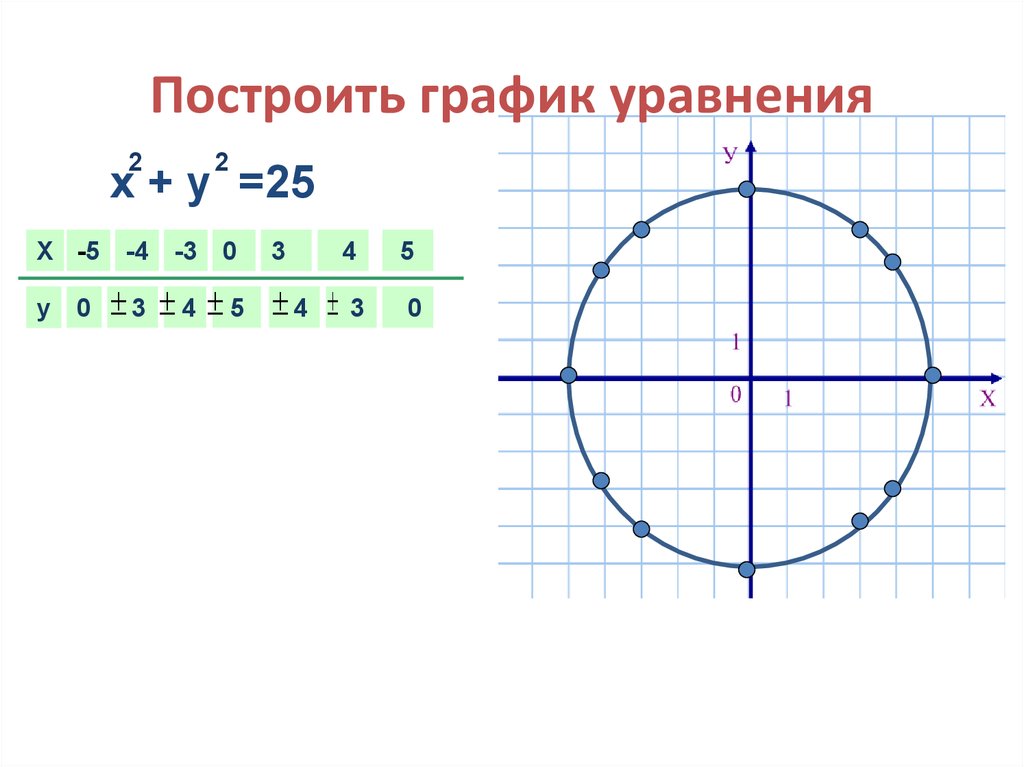
5. Построить график уравнения

2
2
х + у =25
X -5
y
0
-4
-3
0
3
3 4 5 4
4
3
5
0

6. Графиком уравнения (х-а) +(у-b) =r является окружность с центром в точке О (а,b) и радиусом r.

Графиком уравнения
2
2
2
(х-а) +(у-b) =r является
окружность с центром в
точке О (а,b) и радиусом r.
r
а
b

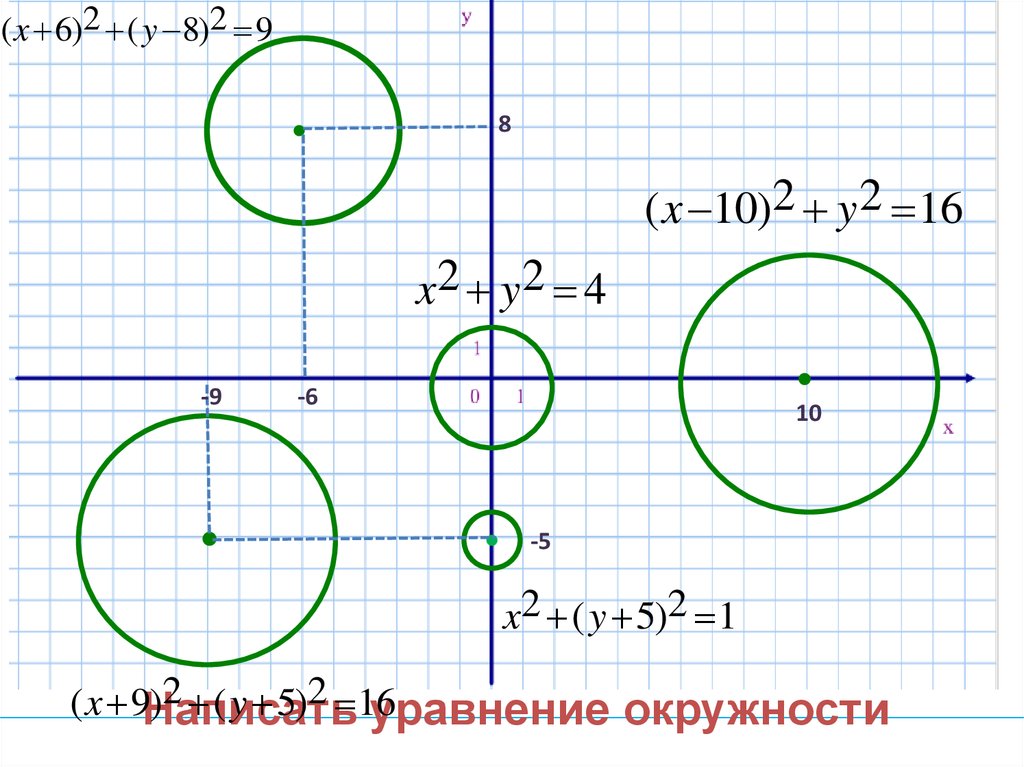
7.

( x 6)2 ( y 8)2 9
8
( x 10)2 y 2 16
x2 y 2 4
-9
-6
10
-5
x2 ( y 5)2 1
( x 9Написать
)2 ( y 5)2 16
уравнение окружности

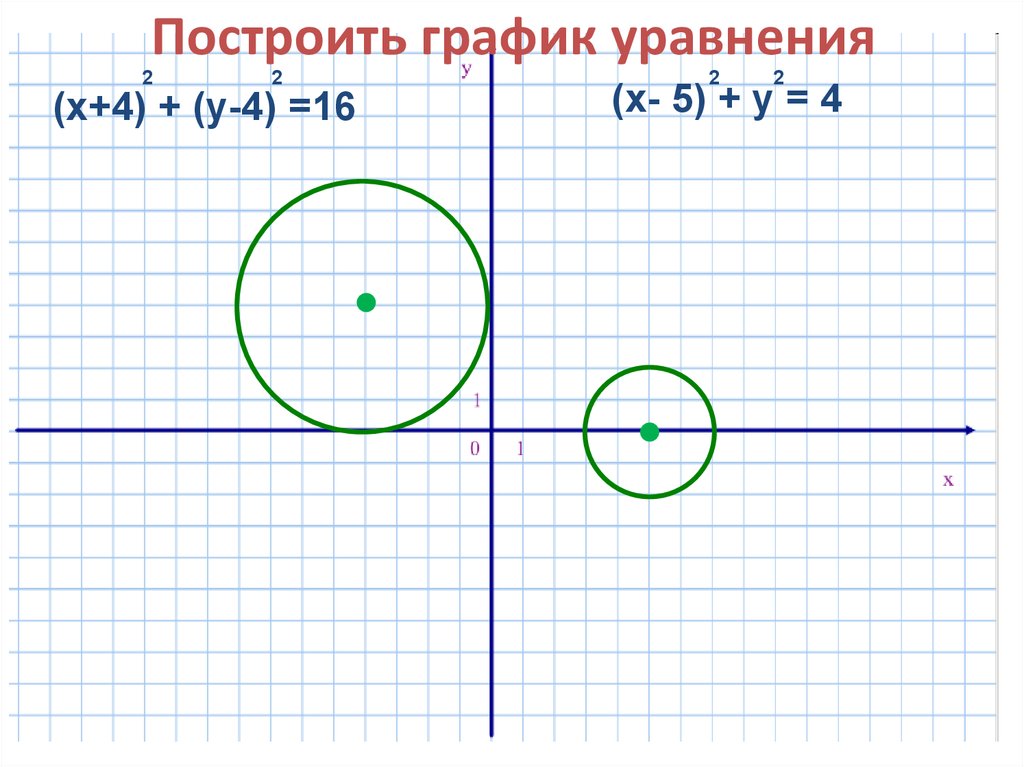
8. Построить график уравнения

2
2
(х+4) + (у-4) =16
2
2
(х- 5) + у = 4

9.

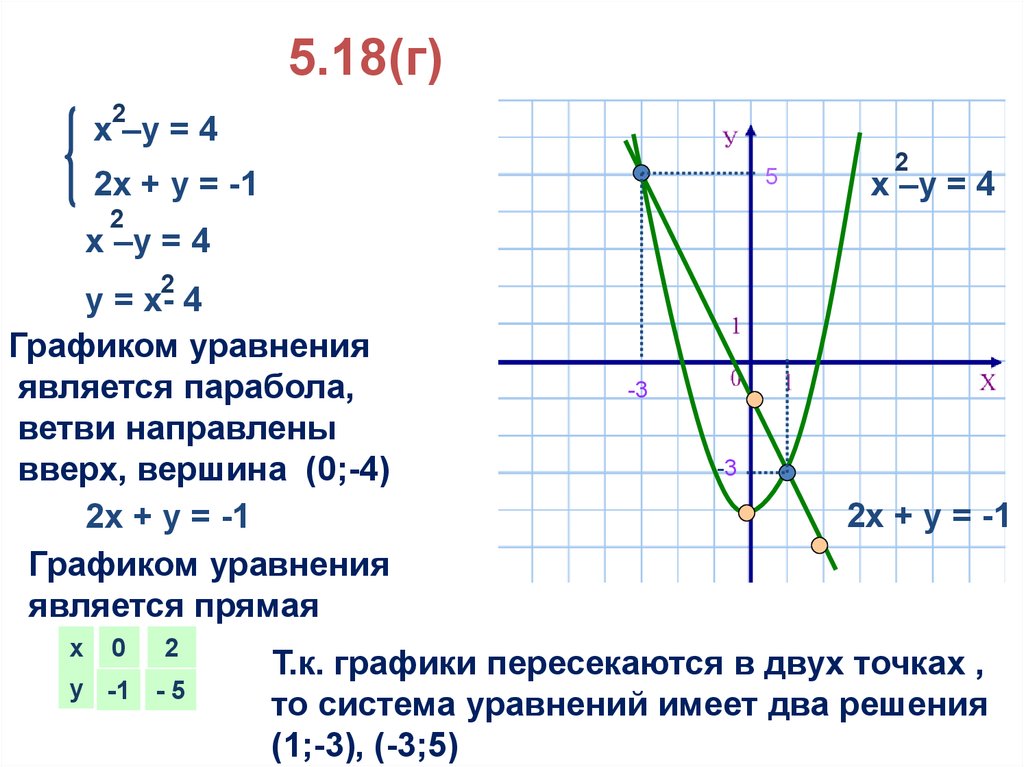
5.18(г)
2
х –у = 4
2х + у = -1
5
2
х –у = 4
2
х –у = 4
2
у = х- 4
Графиком уравнения
является парабола,
ветви направлены
вверх, вершина (0;-4)
2х + у = -1
Графиком уравнения
является прямая
х
0
2
у -1 - 5
-3
-3
2х + у = -1
Т.к. графики пересекаются в двух точках ,
то система уравнений имеет два решения
(1;-3), (-3;5)

10.

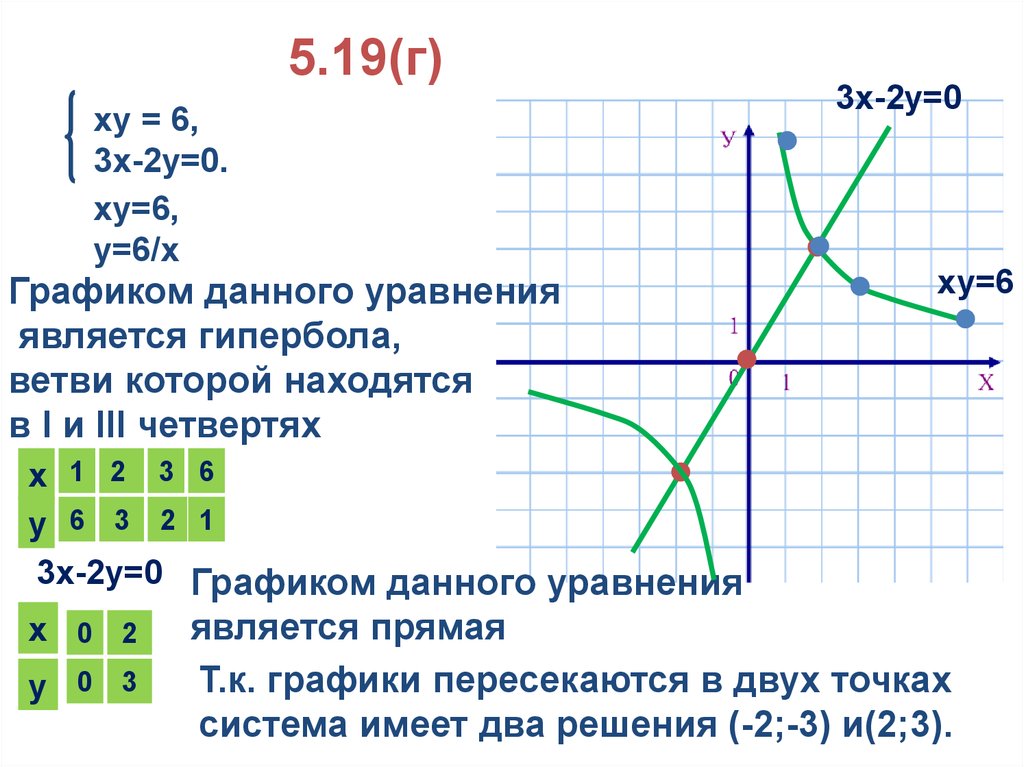
5.19(г)
ху = 6,
3х-2у=0.
ху=6,
у=6/х
Графиком данного уравнения
является гипербола,
ветви которой находятся
в I и III четвертях
3х-2у=0
ху=6
х 1 2 3 6
у 6 3 2 1
3х-2у=0 Графиком данного уравнения
является прямая
х 0 2
у 0 3
Т.к. графики пересекаются в двух точках
система имеет два решения (-2;-3) и(2;3).

11.

5.20 (г)
2
2
(х+2) +(у-2) =1
у = х+1
2
2
2
(х+2) +(у-2) =1
у = х+1
2
(х+2) +(у-2) =1
Графиком уравнения является
окружность с центром
в точке (-2;2) радиуса 1
График уравнения у = х+1
получается из графика у= х
параллельным переносом вдоль оси ОХ на 1 влево
Т.к. графики уравнений не пересекаются,
то система не имеет решений

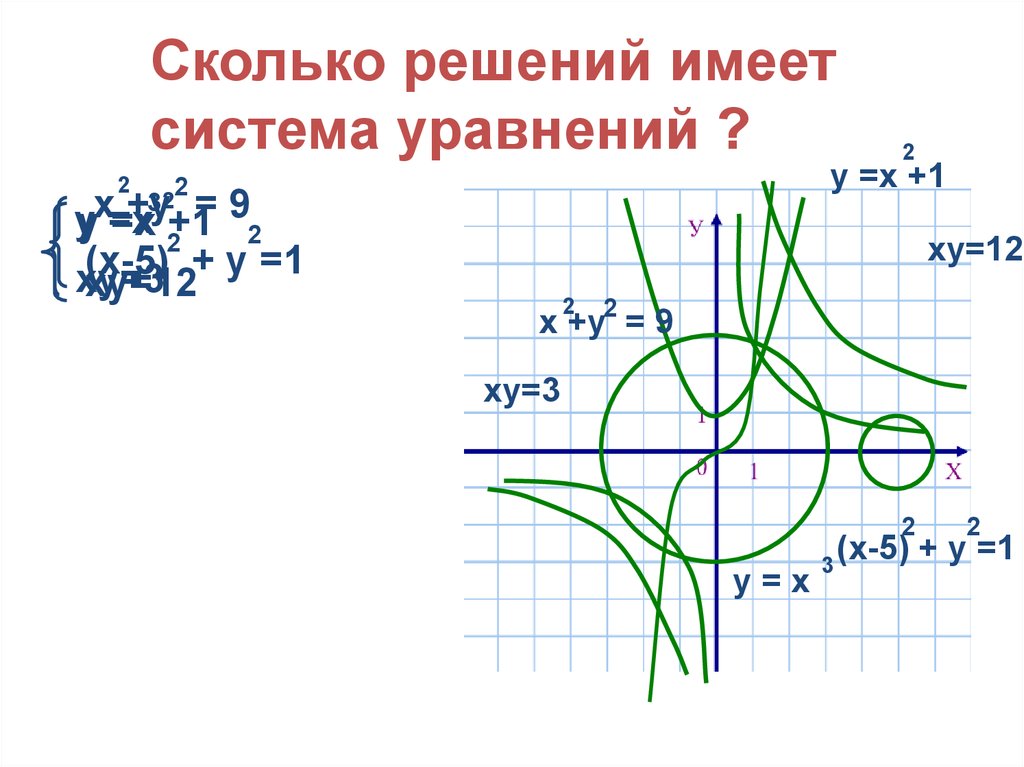
12.

Сколько решений имеет
система уравнений ?
2
у =х +1
2
+у+1= 9
ух=х
2
2
(х-5) + у =1
ху=3
ху=12
2
32
ху=12
2
х +у2 = 9
ху=3
2
у=х
3
2
(х-5) + у =1

13.

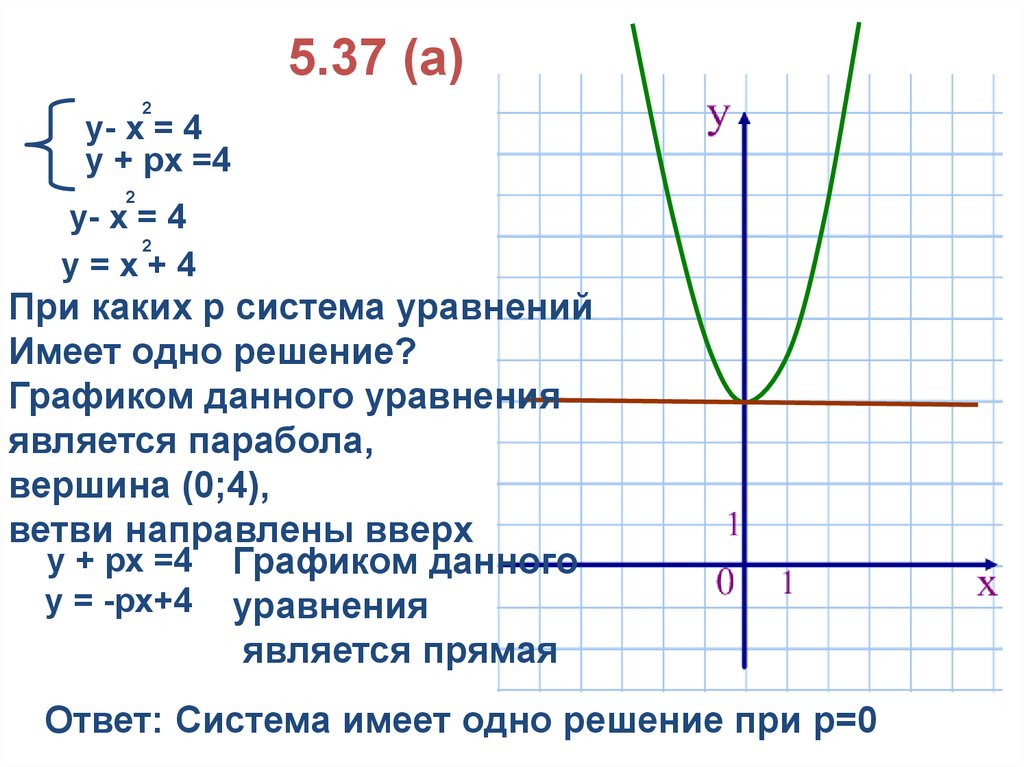
5.37 (а)
2
у- х = 4
у + рх =4
2
у- х = 4
2
у=х+4
При каких р система уравнений
Имеет одно решение?
Графиком данного уравнения
является парабола,
вершина (0;4),
ветви направлены вверх
у + рх =4 Графиком данного
у = -рх+4 уравнения
является прямая
Ответ: Система имеет одно решение при р=0

14.

2
2
2
2
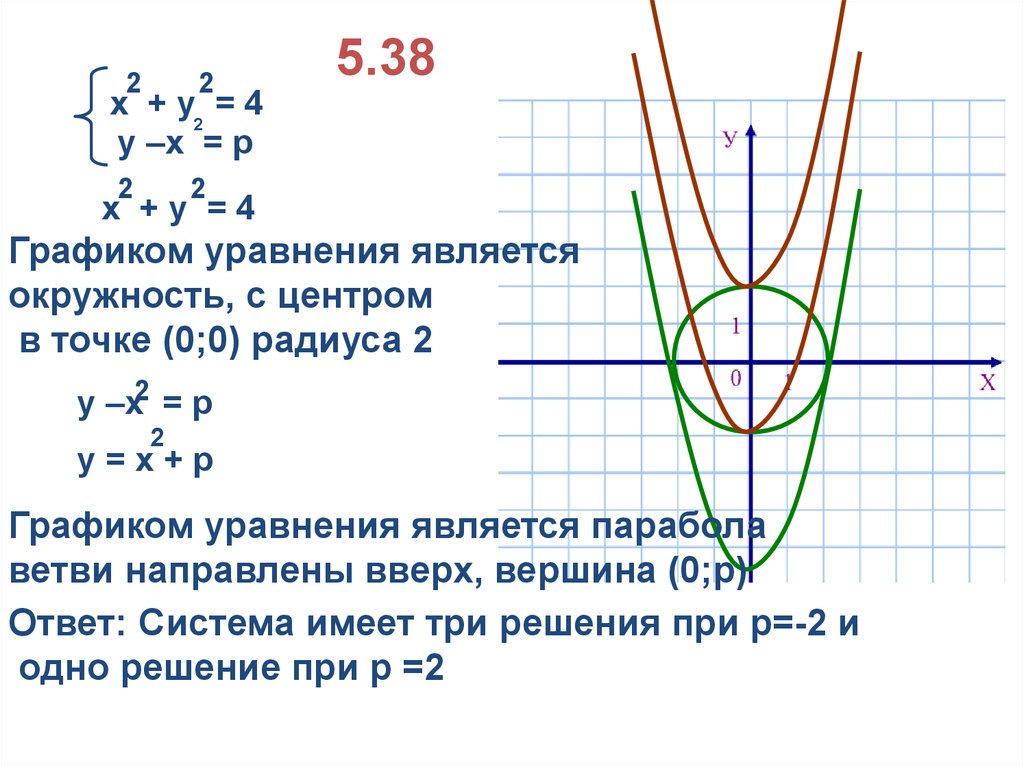
х + у2 = 4
у –х = р
5.38
х +у =4
Графиком уравнения является
окружность, с центром
в точке (0;0) радиуса 2
у –х2 = р
2
у=х+р
Графиком уравнения является парабола
ветви направлены вверх, вершина (0;р)
Ответ: Система имеет три решения при р=-2 и
одно решение при р =2

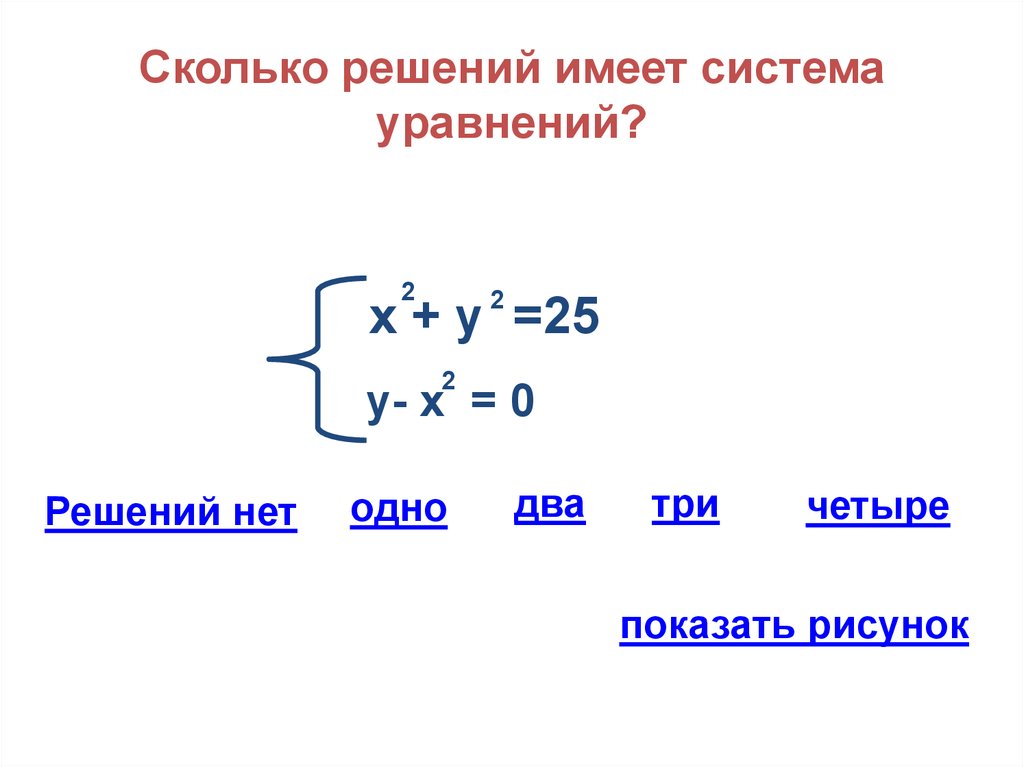
15. Сколько решений имеет система уравнений?

2
х + у =25
2
2
у- х = 0
Решений нет
одно
два
три
четыре
показать рисунок

16.

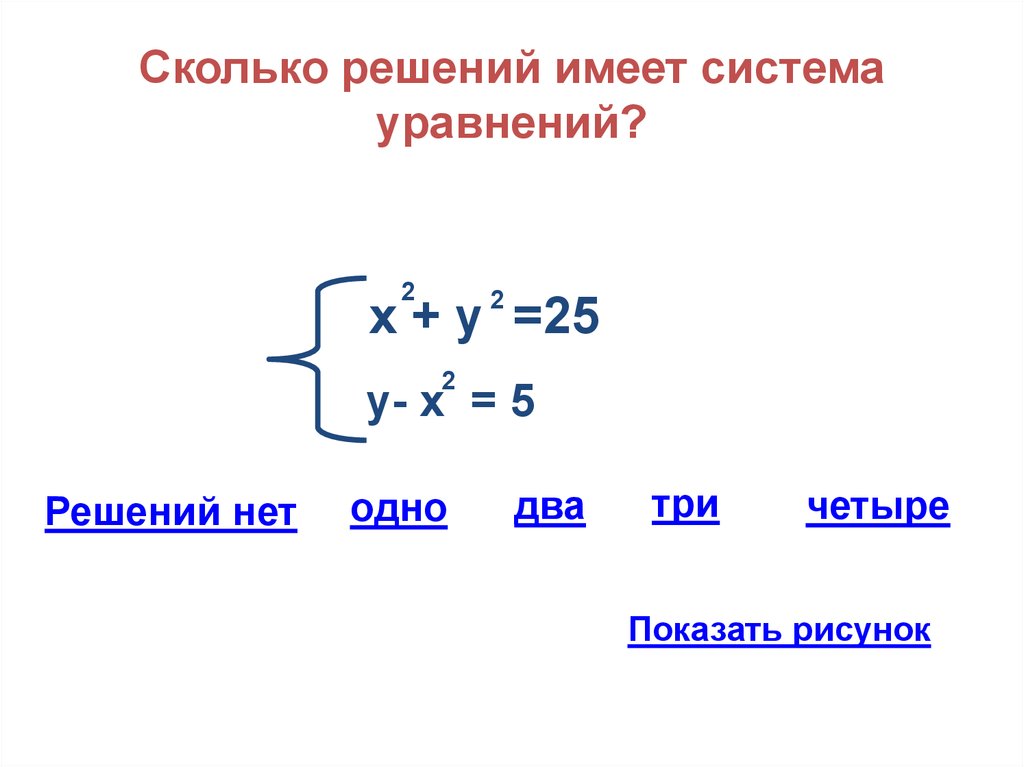
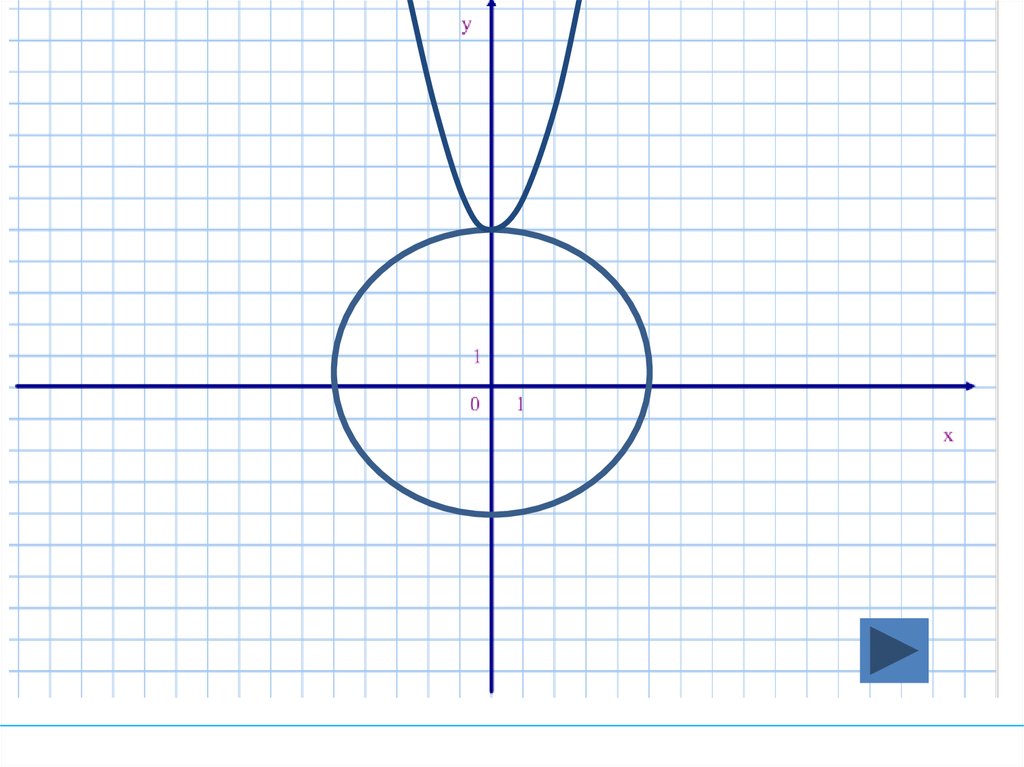
17. Сколько решений имеет система уравнений?

2
х + у =25
2
2
у- х = 5
Решений нет
одно
два
три
четыре
Показать рисунок

18.

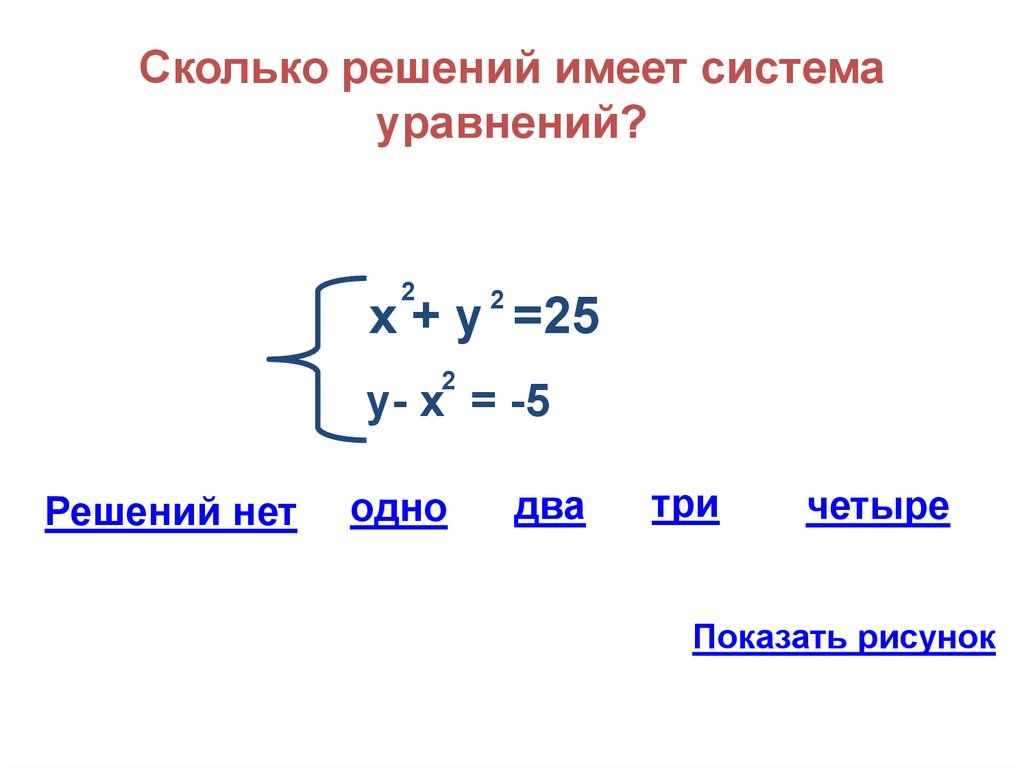
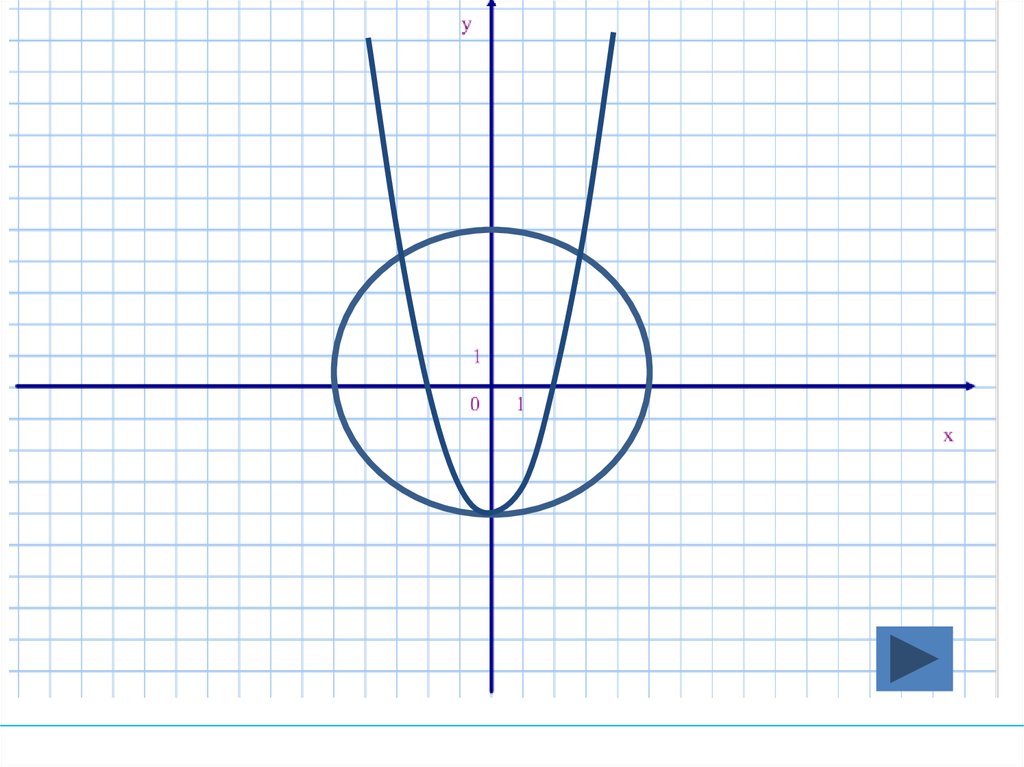
19. Сколько решений имеет система уравнений?

2
х + у =25
2
2
у- х = -5
Решений нет
одно
два
три
четыре
Показать рисунок

20.

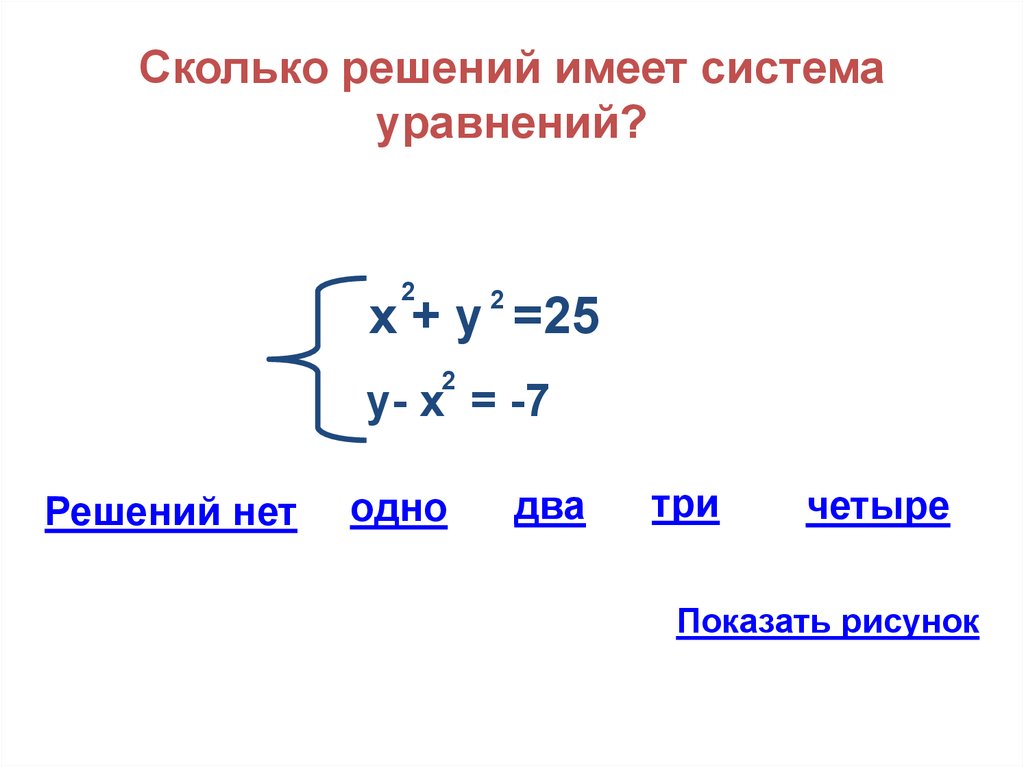
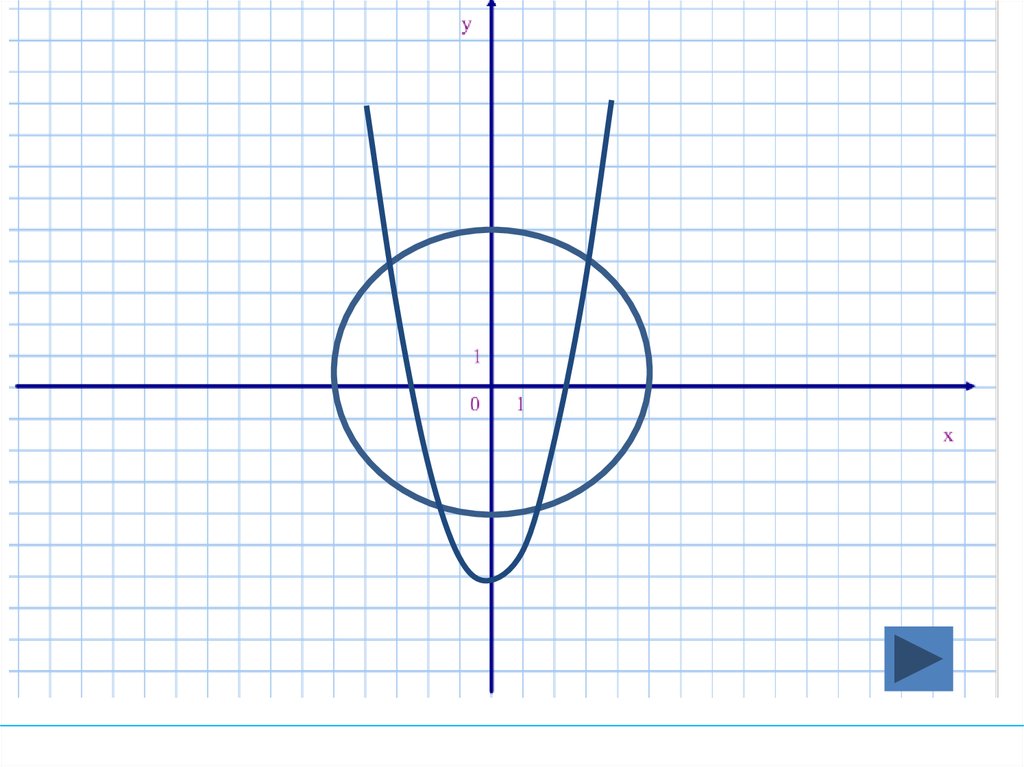
21. Сколько решений имеет система уравнений?

2
х + у =25
2
2
у- х = -7
Решений нет
одно
два
три
четыре
Показать рисунок

22.

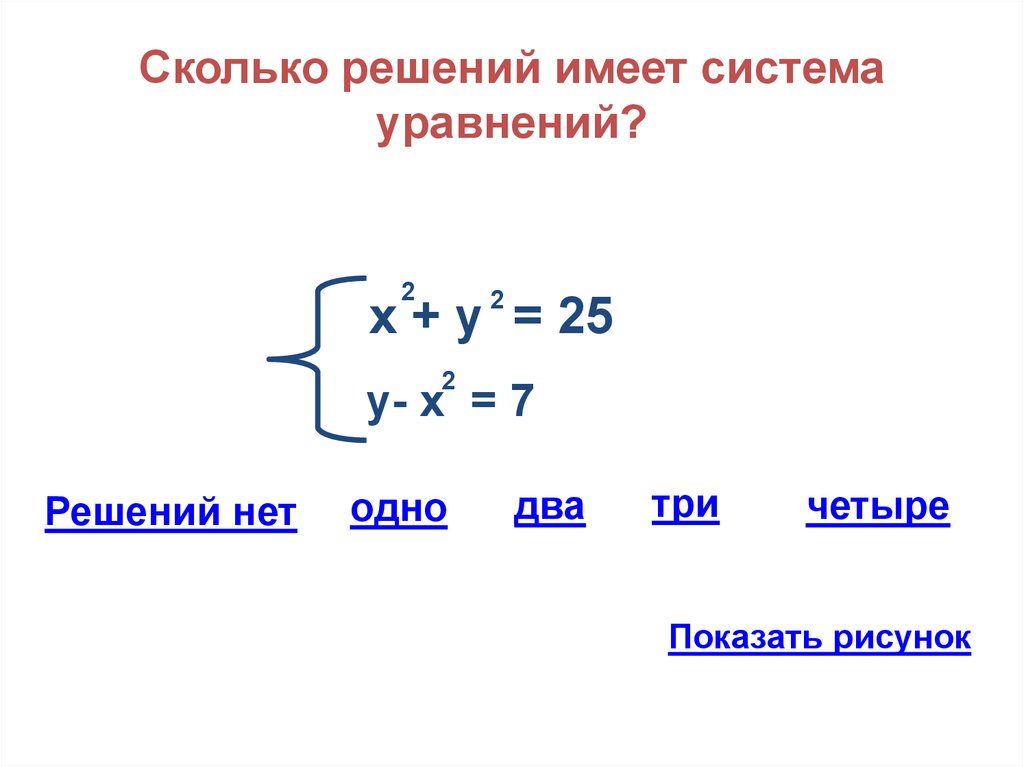
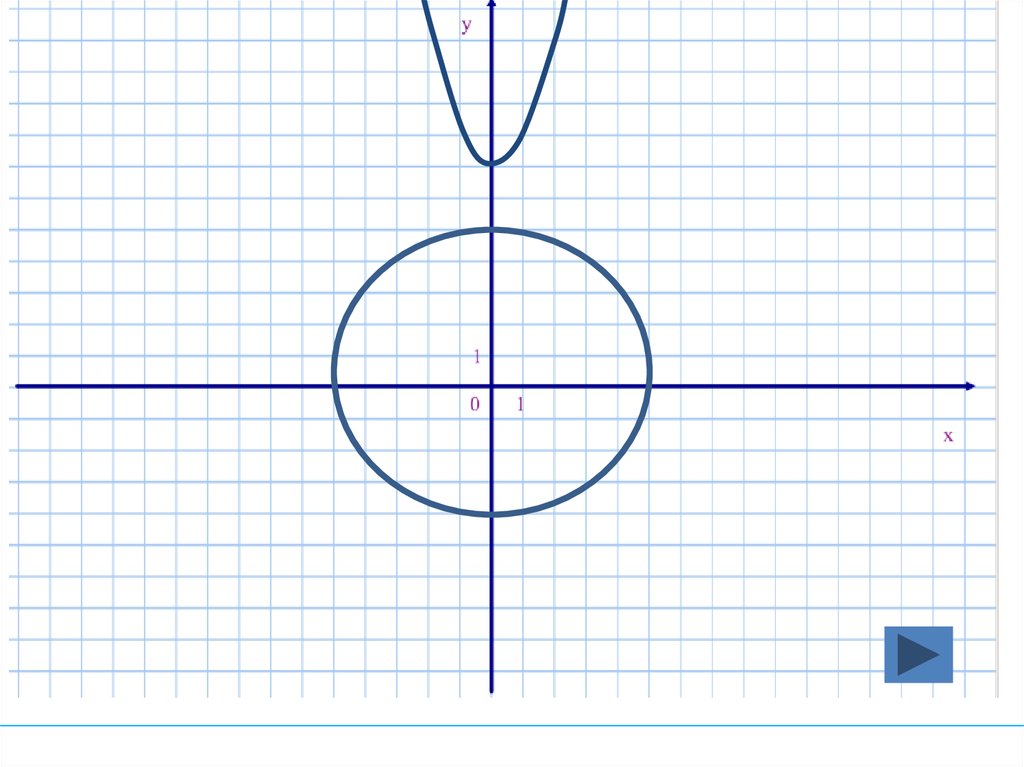
23. Сколько решений имеет система уравнений?

2
х + у = 25
2
2
у- х = 7
Решений нет
одно
два
три
четыре
Показать рисунок

24.

25. Вопросы рефлексии

• Каковы мои главные результаты сегодня?
• Какие трудности встретились во время
выполнения заданий? Как я их
преодолевал?
• Что я узнал нового на уроке?
• Что вызвало интерес?