Похожие презентации:
Теория перемещений. Основные понятия и теоремы
1.
Теория перемещений. Основные понятия и теоремыПод перемещением какой-либо точки сооружения понимается изменение ее
координат в результате деформации элементов сооружения.
Основные гипотезы, используемые при определении перемещений:
- рассматриваются линейно деформируемые системы, подчиняющиеся закону Гука:
= k P,
где k - коэффициент пропорциональности.
- используется принцип суперпозиции (наложения), согласно которому результат
действия системы сил равен сумме результатов действия отдельных сил:
кр = P1 к,1 + P2 к,2 + ...... + Pn кn ,
где
кp - перемещение системы, первый индекс показывает точку и направление
перемещения, а второй - причину вызвавшую перемещение;
кn - перемещение в направлении k от действия силы Рn=1.
- используются понятия обобщенной силы и обобщенного перемещения:
а) под обобщенной силой понимается любая сила или группа сил (например: пара сил,
равномерно распределенная нагрузка и т.п.).
б) обобщенное перемещение - это перемещение, соответствующее обобщенной силе, которое
при умножении на обобщенную силу дает работу, т.е. это множитель при обобщенной силе в
выражении работы:
P
P
A = P l ,
здесь l -обобщенное перемещение для двух сил Р.
l
l
2.
Теория перемещений. Основные понятия и теоремыДействительная и возможная (виртуальная) работа внешних сил
При статическом приложении силы Р, т.е. при постепенном возрастании силы от
нуля до своего конечного значения, зависимость между перемещением и значением силы
Р выражается диаграммой
A
P
0
P
A1
Работу силы Р на перемещении определяет площадь треугольника ОАА1 :
1
A=
P ,
2
т.е. при действии на упругую систему статической силы, действительная работа этой силы
равна половине произведения конечного значения этой силы на конечное перемещение.
Действительная работа системы сил, при статическом их действии:
1 n
A = P i i ,
2 i 1
При статическом действии момента или распределенной нагрузки:
1
1
A = M ;
A = q y( x )dx .
2l
2
(1)
3.
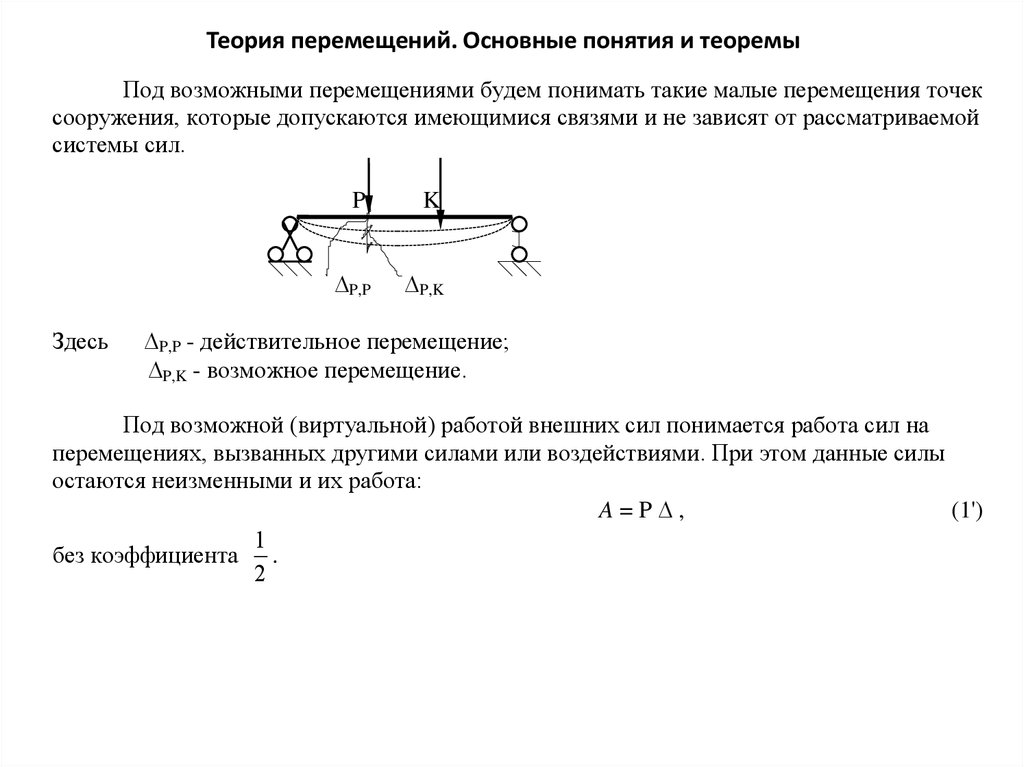
Теория перемещений. Основные понятия и теоремыПод возможными перемещениями будем понимать такие малые перемещения точек
сооружения, которые допускаются имеющимися связями и не зависят от рассматриваемой
системы сил.
Здесь
P
K
P,P
P,K
P,P - действительное перемещение;
P,K - возможное перемещение.
Под возможной (виртуальной) работой внешних сил понимается работа сил на
перемещениях, вызванных другими силами или воздействиями. При этом данные силы
остаются неизменными и их работа:
A=P ,
(1')
1
без коэффициента .
2
4.
Теория перемещений. Основные понятия и теоремыТеоремы о взаимности работ и взаимности перемещений
Рассмотрим два случая последовательного загружения упругой системы силами Р1
и Р2 , изменяя очередность загружения этими силами. Запишем работу сил 1-го и 2-го
состояний.
1.
P1
1,1
P2
1,2
A1 =
1
1
P1 1,1 + P1 1,2 + P2 2,2 ;
2
2
A2 =
1
1
P1 1,1 + P2 2,2 + P2 2,1
2
2
2,2
2.
P1
1,1
P2
2,2
2,1
Т.к. для обоих случаев начальное и конечное состояния одинаковы, следовательно,
в обоих вариантах загружения произведена одна и та же работа. Приравняв их, получим:
P1 12 = P2 21 ,
(2)
или
A12 = A21 .
(3)
Для двух состояний упругой системы виртуальная работа сил 1-го состояния
на перемещениях, вызванных силами второго состояния, равна виртуальной работе
сил 2-го состояния на перемещениях, вызванных силами 1-го состояния. (Теорема
Бетти).
5.
Потенциальная энергия упругой системыРабота внешних сил на вызванных ими перемещениях может быть выражена через
внутренние усилия, возникающие в поперечных сечениях стержневой системы. В общем
случае в элементе dx возникают усилия:
Q
Q
M
M
N
N
dx
Усилия N, M, Q являются внутренними усилиями по отношению к стержню.
Однако, для выделенного элемента они являются внешними силами, а потому работу А
можно получить как сумму работ, совершенных статически возрастающими усилиями N,
M, Q на соответствующих деформациях.
6.
Потенциальная энергия упругой системыРабота внешних сил на вызванных ими перемещениях может быть выражена через
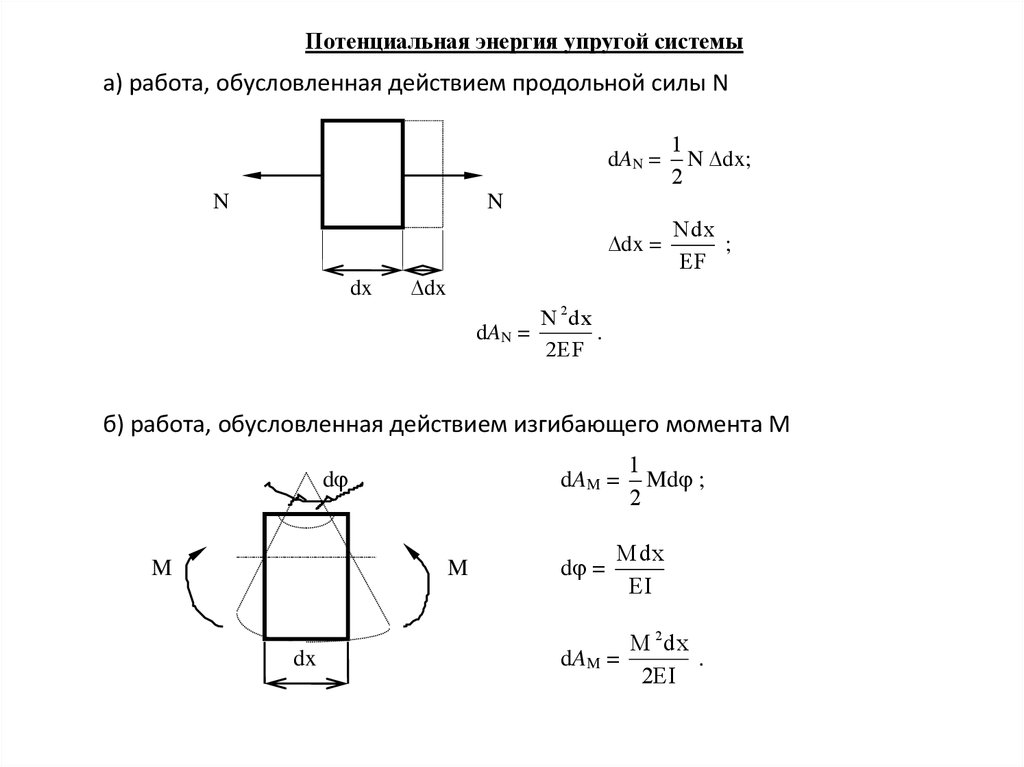
a)
работа,
обусловленная
действием
продольной
N
внутренние усилия,
возникающие
в поперечных
сеченияхсилы
стержневой
системы. В общем
случае в элементе dx возникают усилия:
1
dAN = N dx;
Q
Q
2
M
M
N
N
N
N
Ndx
dx =
;
EF
dx
dx
dx
N 2 dx
dAN =
.
2
EF
Усилия N, M, Q являются внутренними усилиями по отношению к стержню.
Однако, для выделенного элемента они являются внешними силами, а потому работу А
можно получить как сумму работ, совершенных статически возрастающими усилиями N,
б) работа, обусловленная действием изгибающего момента М
M, Q на соответствующих деформациях.
1
d
dAM = Md ;
2
M
M
dx
d =
Mdx
EI
M 2 dx
dAM =
.
2EI
7.
Потенциальная энергия упругой системыРабота внешних сил на вызванных ими перемещениях может быть выражена через
в)
работа,
обусловленная
действием
поперечной
Q
внутренние усилия,
возникающие
в поперечных
сеченияхсилы
стержневой
системы. В общем
случае в элементе dx возникают усилия:
1
dAQ =
Q
M
Q
N
Q
Q
2
Q y
M
y
N y = dx = dx
G
dx
dx
Предположим, что касательные напряжения равномерно распределены по всей
Усилия N, M, Q являются внутренними усилиями
по отношению1 кQстержню.
2
Qdx
dx
площади
т.е. = Qэлемента
/ F . Тогда:
,силами,
dAQ =а потому работу
.
Однако,сечения,
для выделенного
они являются внешними
А
y=
2 GFусилиями N,
GF возрастающими
можно получить как сумму работ, совершенных статически
В действительности
касательные
напряжения распределены по площади поперечного
M, Q на соответствующих
деформациях.
сечения неравномерно, что учитывается введением поправочного коэффициента :
1 Q 2 dx
.
dAQ =
2 GF
8.
Потенциальная энергия упругой системыРабота внешних сил на вызванных ими перемещениях может быть выражена через
Полная усилия,
работа внешних
сил,ввыраженная
внутренние
усилия:
внутренние
возникающие
поперечных через
сечениях
стержневой
системы. В общем
l
l
l
2
2
2
случае в элементе dx M
возникают
усилия:
dx
N dx
Q dx
A=
.
(5)
2EI Q
2EF
0
Q 0 2GF
На основании M
закона сохранения энергии
M работа А внешних сил переходит в
N
потенциальную энергию U деформации,
т.е. N
l
l
l
M 2dx
N 2dx
Q2dx
U =
.
(6)
2EI
2EF
2GF
0
0 dx
0
Возможная работа внешних сил, выраженная через внутренние усилия M1, N1, Q1,
Усилия N, M,
усилиями по отношению к стержню.
M 2Q
dxявляются
N 2dx внутренними
Q2dx
на перемещениях
Однако, для выделенного, элементаи они являются внешними силами, а потому работу А
EF совершенных
GF
можно получить какEI
сумму работ,
статически возрастающими усилиями N,
l
l
l
M, Q на соответствующих
деформациях.
M1M
N1N 2dx
Q Q dx
2dx
A1,2 =
(7)
1 2 .
EI
EF
GF
0
0
0
0
9.
Интеграл Мора для определения перемещенийПусть требуется определить вертикальное перемещение точки К при действии на
сооружение заданной нагрузки. Рассмотрим два состояния системы : под действием
заданной нагрузки - состояние 1; и по направлению искомого перемещения приложим
силу Р=1 - состояние 2.
K
1)
P2 =1 K
q
2)
21
Работа А21 сил второго состояния Р2 = 1 на перемещениях, вызванных силами первого
состояния 21:
A21 = P2 21 учитывая, чтоР2=1,
21 = A21 .
Выразим А21 через внутренние усилия в стержнях системы
l
l
l
MPMdx
NPNdx
Q Qdx
21 = A21 =
.
(8)
P
EI
EF
GF
0
0
0
Здесь: Mp, Np, Qp - внутренние усилия в стержнях системы от действия внешних нагрузок
(первое состояние); M, N, Q - от действия силы Р=1 (второе состояние).
10.
Порядок определения перемещений с помощью интеграла Мора1) Записывают аналитические выражения усилий Mp, Np, Qp от заданной внешней
нагрузки.
2) По направлению искомого перемещения прикладывают единичную силу Р=1
или единичный момент М=1 (если определяется угол поворота сечения). Записывают
выражения усилий M, Q, N от единичной силы.
3) Полученные аналитические выражения усилий Mp, Np, Qp и M, Q, N
подставляют в правую часть формулы (8) и интегрированием по участкам в пределах
всего сооружения, определяют искомое перемещение.
Примечания: В частных случаях формула Мора принимает более простой вид. Так,
при расчете ферм, в стержнях которых возникают только продольные усилия, формула
имеет вид:
N N dx
N Nl
P
KP = P
,
EF
EF
l
при расчете балок и рам, где влияние на перемещения продольных и поперечных сил
незначительно, формула (8) принимает вид:
M Mdx
KP = P
.
EI
l
11.
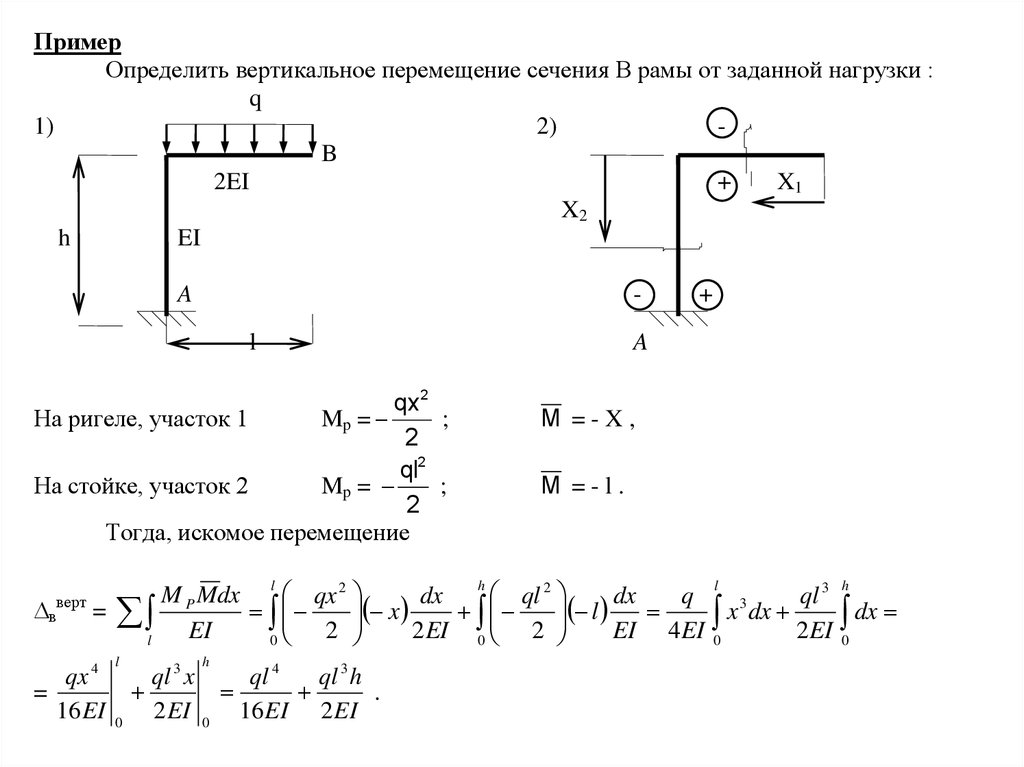
ПримерОпределить вертикальное перемещение сечения В рамы от заданной нагрузки :
q
1)
2)
B
2EI
+
X1
X2
h
EI
A
l
qx2
На ригеле, участок 1
Mp =
;
2
ql2
На стойке, участок 2
Mp =
;
2
Тогда, искомое перемещение
в
верт
+
A
M =-X,
M =-l.
h
l
h
ql 2
M P Mdx l qx 2
dx
dx
q
ql 3
3
x
l
=
x dx
dx
EI
2
2EI 0 2
EI 4EI 0
2EI 0
l
0
qx 4
=
16 EI
l
0
ql 3 x
2 EI
h
0
ql 4
ql 3 h
.
16 EI 2 EI
12.
Вычисление интеграла Мора путем перемножения эпюр(правило Верещагина, формула Симпсона)
Определение перемещений в системах, состоящих из прямолинейных элементов
постоянной жесткости, можно значительно упростить путем применения специальных
приемов вычисления интегралов типа
l
M Mdx
KP = P
.
EI
0
Предположим, что для какого-то элемента системы с постоянной жесткостью
построены эпюры Mp и M , причем одна из них, например M , прямолинейна.
Вычислим:
b
M P Mdx 1 b
a EI EI a M P Mdx .
13.
Вычисление интеграла Мора путем перемножения эпюр(правило Верещагина, формула Симпсона)
Из приведенного ниже рисунка следует, что
b
M
P
M tg •X , тогда:
b
b
a
a
Mdx M P Xtg dx tg XM P dx .
a
ц.т.
d = MP dx
эп. MP
x
dx
x0
y0
M
эп. M
X
a
b
14.
Вычисление интеграла Мора путем перемножения эпюр(правило Верещагина, формула Симпсона)
Вычислим:
b
M P Mdx
1
a EI
EI
b
a
M
P
Mdx .
a
M tg •X , тогда:
Из рисунка следует, что
M
b
P
b
b
a
a
Mdx M P Xtg dx tg XM P dx .
b
Из рисунка MP dx = d , а интеграл
Xd
представляет собой статический момент
a
площади эпюры Мр относительно оси Y. Этот статический момент можно выразить иначе:
b
Xd X
a
b
M
P
0
, где X0 - расстояние от центра тяжести эпюры Мр до оси Y. Тогда:
Mdx X 0 tg , но так как X0 tg = y0 (см. рисунок),
b
то
M
P
Mdx y 0
a
a
M P Mdx y 0
a EI EI .
b
Или
(9)
Таким образом, результат перемножения двух эпюр равен произведению площади
одной из них на ординату y0 другой (прямолинейной) эпюры, взятую под центром
тяжести площади первой эпюры.
15.
Вычисление интеграла Мора путем перемножения эпюр(правило Верещагина, формула Симпсона)
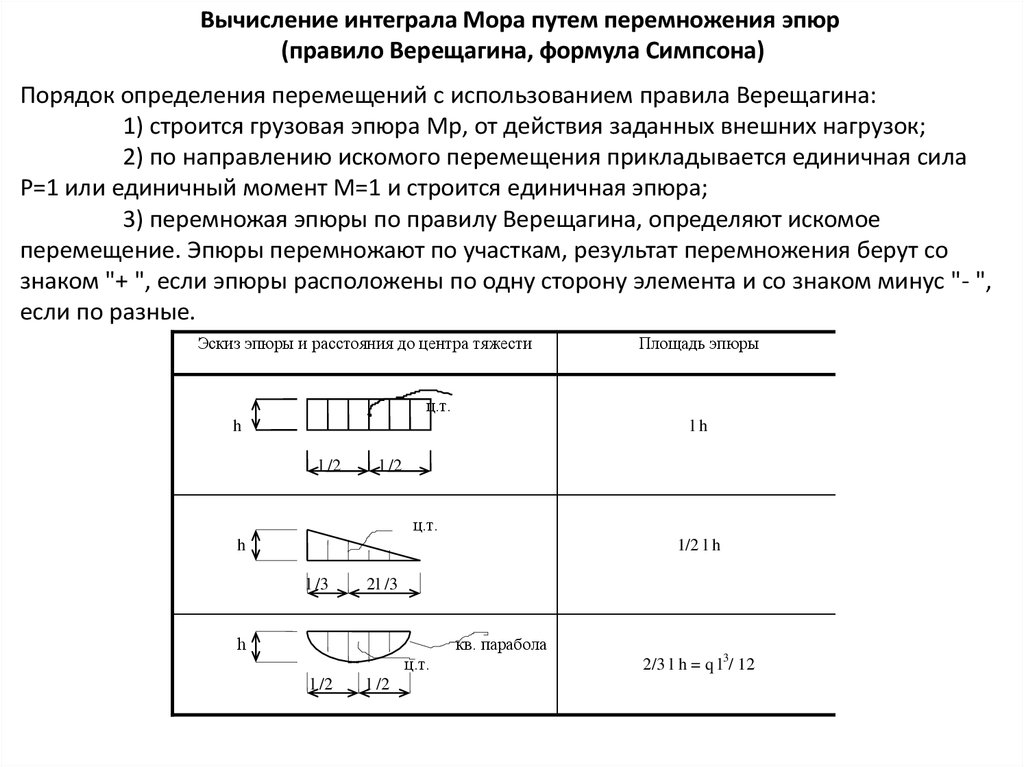
Порядок определения перемещений с использованием правила Верещагина:
1) строится грузовая эпюра Мр, от действия заданных внешних нагрузок;
2) по направлению искомого перемещения прикладывается единичная сила
Р=1 или единичный момент М=1 и строится единичная эпюра;
3) перемножая эпюры по правилу Верещагина, определяют искомое
перемещение. Эпюры перемножают по участкам, результат перемножения берут со
знаком "+ ", если эпюры расположены по одну сторону элемента и со знаком минус "- ",
если по разные.
Эскиз эпюры и расстояния до центра тяжести
Площадь эпюры
ц.т.
h
lh
l /2
l /2
ц.т.
h
1/2 l h
l /3
2l /3
h
кв. парабола
ц.т.
l /2
l /2
2/3 l h = q l3/ 12
16.
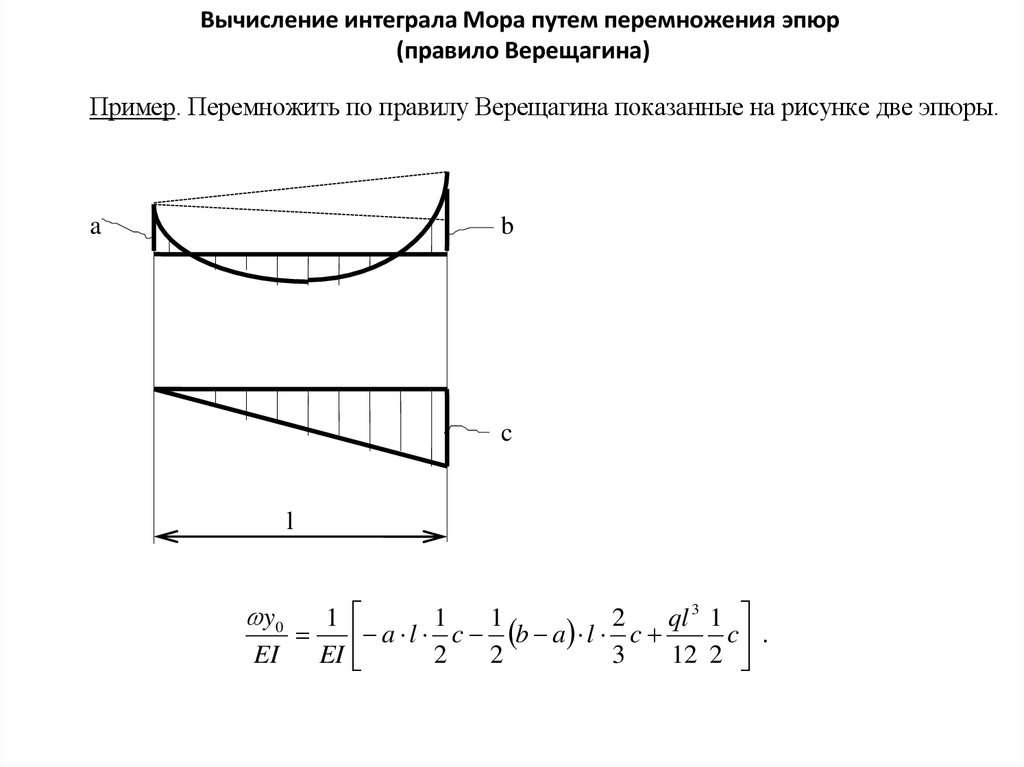
Вычисление интеграла Мора путем перемножения эпюр(правило Верещагина)
Пример. Перемножить по правилу Верещагина показанные на рисунке две эпюры.
a
b
c
l
y0
1
EI
EI
1
1
2
ql 3 1
c .
a l c b a l c
2
2
3
12 2
17.
Вычисление интеграла Мора путем перемножения эпюр(формула Симпсона)
В некоторых случаях интеграл Мора удобно вычислять с помощью формулы
Симпсона-Корноухова. Эта формула применима, если сумма порядков линий эпюр
подинтегральных функций не превышает трех (кубической параболы).
Стержневую систему разбивают на отдельные участки, элементов с постоянной
жесткостью, и на этих участках интеграл Мора вычисляют по формуле:
li
M P Mdx
a c 4 fe bd ,
l EI
6
EI
i
a
f
b
эп. MP
c
e
d
эп M
li
Здесь: f,e - ординаты эпюр Мр и M посредине длины участка.
(10)












 Механика
Механика








