Определение продолжительности нагрева термически массивных тел. Аналитические методы определения времени нагрева

1.

Лекция №14.
.
Определение продолжительности нагрева термически
массивных тел. Аналитические методы определения времени
нагрева
Для ТМТ неприемлемо допущение о равенстве температур поверхности среднемассовой, T
T x , y , z ,τ
Нагрев считается законченным, когда:
1) температура поверхности равна заданной: T R , τ Tз Tпов
кон
2) конечный перепад температур по толщине меньше или равен заданному: T τ Tз T кон
Если T τ T кон, то продолжаем нагрев, но при других ГУ.
Методы определения времени нагрева τ н :
1. Аналитическое решение краевой задачи теплопроводности (КЗТ).
2. Приближенные методы определения
τн
3. Численные методы решения КЗТ.
1

2.

1. ОПРЕДЕЛЕНИЕ ВРЕМЕНИ НАГРЕВА ИЗ
АНАЛИТИЧЕСКОГО РЕШЕНИЯ КЗТ
1.1. ДОПУЩЕНИЯ
1) Реальные тела сводим к одному из тел правильной формы.
2) Граничные условия однородны по поверхности тела.
В результате этих двух допущений – симметричность и одномерность температурного
поля: T T x ,τ
3) Физические свойства не зависят от температуры.
4) Начальные и граничные условия описываются простейшими
уравнениями.
5) Продолжительность нагрева существенно больше длительности
инерционного периода: τн τин (в общем случае τн τин τрег ).
Следовательно, длительность нагрева приближенно равна длительности регулярного
периода: τн τ рег
2

3.

.
.
.
1.2. ПОСТАНОВКА КРАЕВОЙ ЗАДАЧИ
ТЕПЛОПРОВОДНОСТИ
1. Дифференциальное уравнение теплопроводности Фурье:
2T 2 ν 1 T
T
; T T ( x , ).
a 2
τ
x
x
x
2. Геометрические условия задачи: ν, 0 x R ; R – характерный размер.
3. Физические условия задачи:
λ const
c const
a λ/(ρc) const
ρ const
4. Начальные и граничные условия. ГУ: qр.м const; qр.м λ
Начальные условия (НУ): T x ,0 T0 Tнач
T
x
x R
1.3. РЕШЕНИЯ УРАВНЕНИЯ ФУРЬЕ
Случай 1:
qр.м const (ГУ 2 рода).
2
qр.м R
1
x
2 ν 2 Fo 2 ν 2
T x , τ T0
λ
2 R
2 2 ν 4
3

4.

.
.
.
.
При x R
при
x 0
T R ,τ T0
qр.м R
1
2ν 2
2 ν 2 Fo
λ
2 2 2 ν 4
T 0,τ T0
qр.м R
2ν 2
2 ν 2 Fo
λ
2 2 ν 4
В результате перепад температур по толщине тела:
T T R , τ T 0 , τ
qр.м R
λ
const
Скорость подъема температуры во всех точках тела
одинакова, перепад температур по толщине T const
Случай 2:
T R ,τ const (ГУ 1 рода).
x 2
Начальные. условия (НУ): T x ,0 T R ,0 T 0 1
R
T 0 – перепад температур по всему характерному размеру.
4

5.

.
.
.
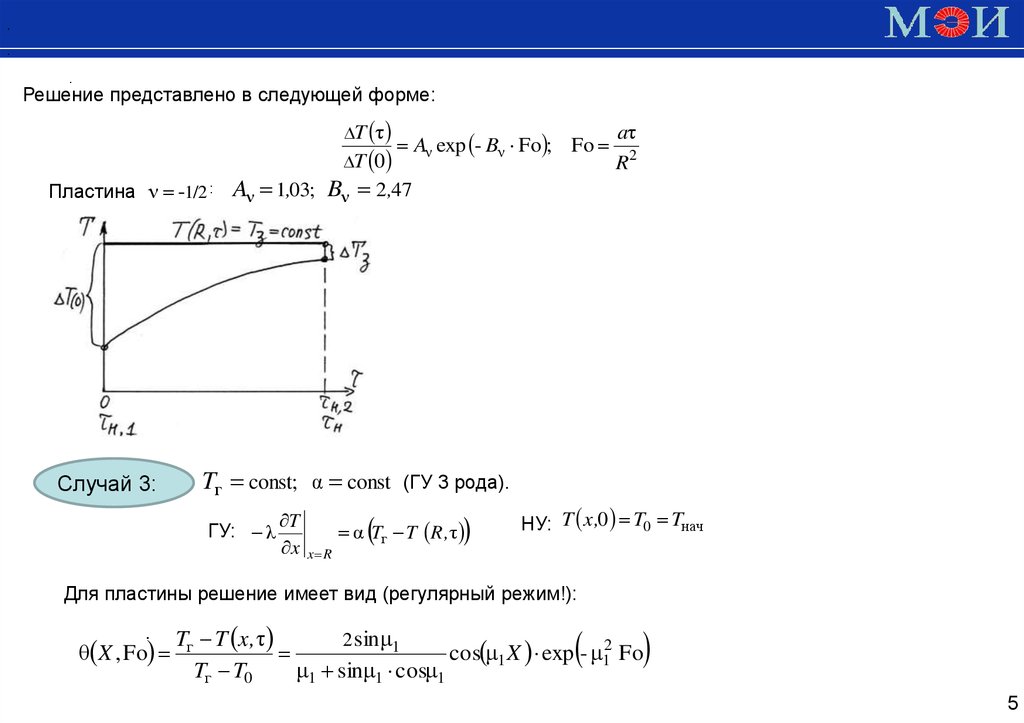
Решение представлено в следующей форме:
T τ
T 0
Пластина ν -1/2 :
Случай 3:
Aν exp - Bν Fo ; Fo
Aν 1,03; Bν 2 ,47
Tг const; α const
ГУ: λ
T
x
x R
aτ
R2
(ГУ 3 рода).
α Tг T R , τ
НУ: T x ,0 T0 Tнач
Для пластины решение имеет вид (регулярный режим!):
.
θ X , Fo
Tг T x , τ
2 sinμ1
cos μ1 X exp - μ12 Fo
Tг T0
μ1 sinμ1 cosμ1
5

6.

.
.
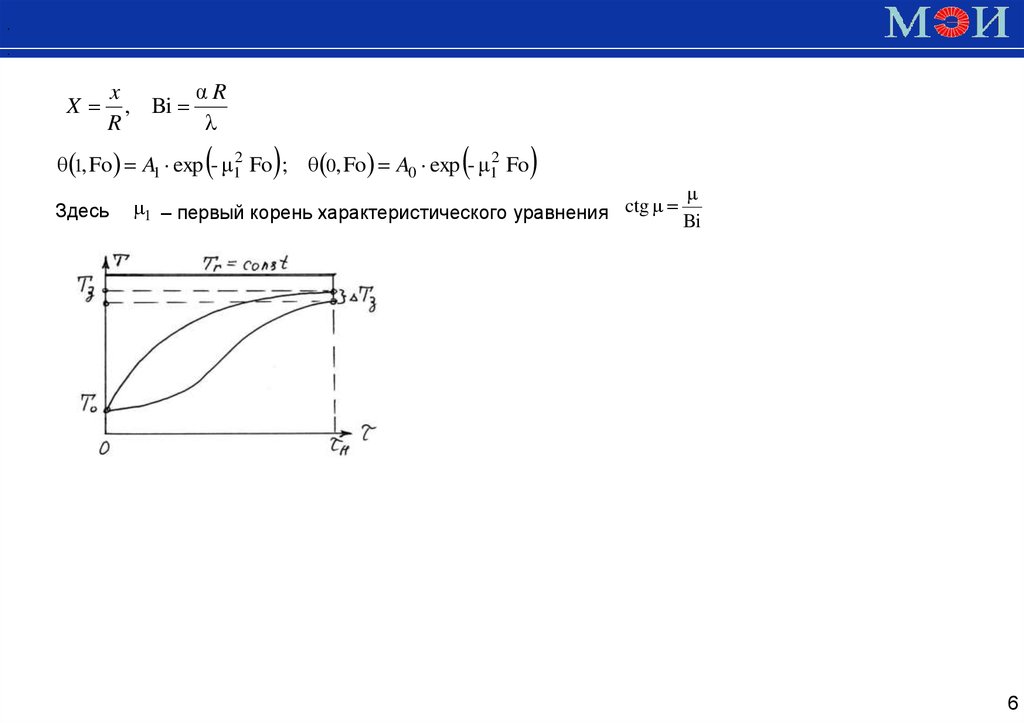
X
x
αR
, Bi
R
λ
θ 1, Fo A1 exp - μ12 Fo ; θ 0, Fo A0 exp - μ12 Fo
Здесь
μ
μ1 – первый корень характеристического уравнения ctg μ
Bi
6

7. Спасибо за внимание!!!

7