Молекулярная физика и термодинамика

1.

Молекулярная физика и термодинамика –
разделы
физики,
в
которых
изучаются
макроскопические процессы в телах, связанные с
огромным числом содержащихся в них атомов и
молекул.
Объект
исследования:
макроскопические системы объекты, состоящие из очень
большого числа частиц (молекул,
атомов).
атом
вещество

2. ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ

3.

Основы
классической
статистики
заложены
Д.К.Максвеллом (Англия), Л.Больцманом (Германия),
В.У.Гиббсом (США) во второй половине XIX столетия.
Задачи статистики
1.
Нахождение средних и наиболее вероятных
значений физических характеристик частиц,
образующих макроскопическую систему.
2.
Выяснение связи между характеристиками
отдельных частиц системы и параметрами всей
системы.

4.

В средине XIX века была сформулирована
молекулярно-кинетическая теория, но тогда не было
никаких доказательств существования самих молекул.
Вся теория базировалась на предположении о
движении молекул, но как измерить скорость их
движения, если они невидимы.
R
3kT
3kN AT
m0 кв2 3
3RT
кв
kT
m0
m0 N A
2
2
µ
m
P RT
m
P
RT
PV RT
P RT
V
кв
Пр: При плотности азота, равной 1.25 кг/м3,
при t=0 С и Р=1 атм., υ=500м/с.
Для водорода: υ=2000м/с.
3P

5.

Проверка факта, что атомы и молекулы
идеальных
газов
в
термически
равновесном пучке имеют различные
скорости, была осуществлена немецким
ученым Отто Штерном в 1920 г.
Место попадания
самых медленных
молекул
Отто Штерн
(1888 1969)
Распределение
молекул по
скоростям
T=1200ºC
Теория: υкв=584 м/с
Место попадания
самых быстрых
молекул
Эксперимент:
560≤υ≤640 м/с

6.

Закономерности, обусловленные большим числом
сталкивающихся атомов и молекул, и не свойственные
отдельным
атомам
и
молекулам,
называются
вероятностными или статистическими.
По определению: Вероятность Р можно
представить как отношение числа благоприятных
случаев к числу возможных случаев.
Отсюда следует, что Р может принимать значения от
нуля до единицы.
Распределение вероятностей – это закон, описывающий область значений переменной и вероятность
появления переменной в конкретных областях значений.
Статистический анализ, для построения рядов
распределения, проводится во многих областях науки с
целью выделения характерных свойств и закономерностей
изучаемой совокупности.

7.

Сколько времени вы проводите за
компьютером?
Распределение пользователей
интернета по возрасту, в %
5
4
3
2
1
0
1
6
11
16
21
t, часы
Для корректного построения распределения нужно
большое количество людей в выборке исследования.

8.

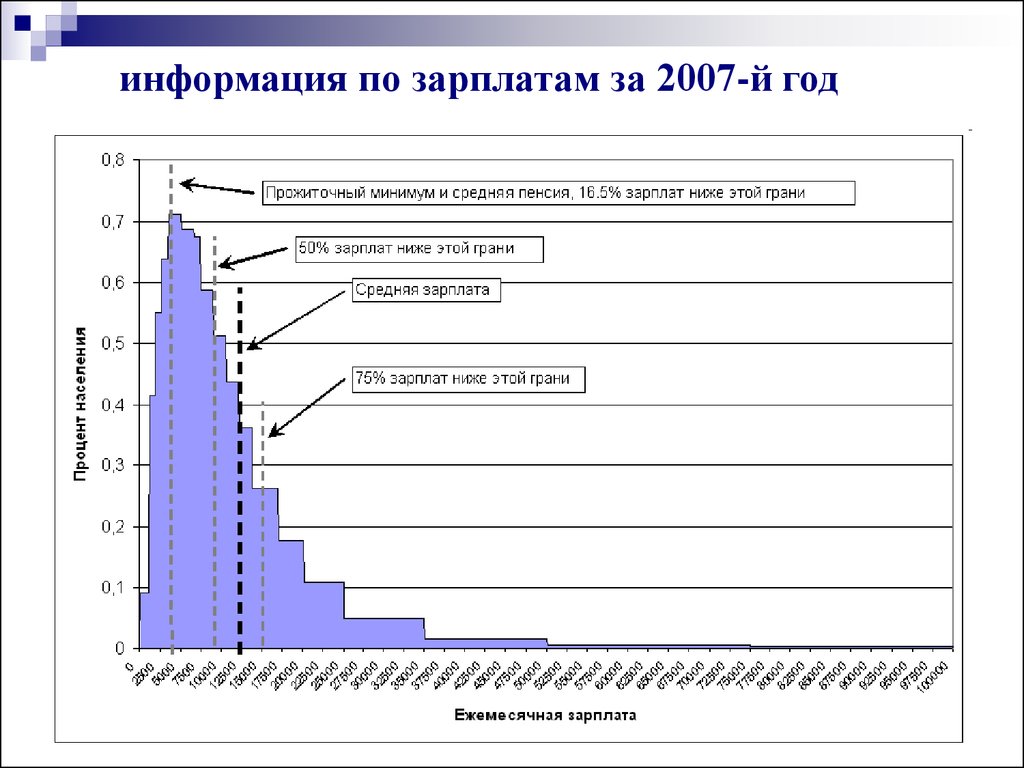
информация по зарплатам за 2007-й год

9. 1. Распределение Максвелла

(для описания распределения молекул по скоростям)

10.

Обозначим:
dN – число молекул со скоростями от υ до υ + dυ.
N – общее число молекул газа в данном объеме.
dN – относительное число молекул, скорости
N
которых лежат в интервале от υ до υ + dυ
(вероятность того, что скорость данной
молекулы лежит в данном интервале ).
dN
– относительное число молекул в единичном
Nd интервале скоростей.
dN
– плотность вероятности того, что
f ( )
Nd молекула обладает скоростью υ
(функция распределения Максвелла).

11.

Явный вид функции f(υ) был получен
теоретически Максвеллом в 1859 г.
m0
f (V ) 4
2 kT
3/ 2
m0 2
e 2 kT
2
Джеймс Клерк
Максвелл
(1831- 1879)
Дж
k 1.38 10
– постоянная Больцмана;
К
m0 – масса молекулы,
23
Т – абсолютная температура газа,
υ – заданная скорость (аргумент функции).
Распределение Максвелла справедливо для газов и
жидкостей.

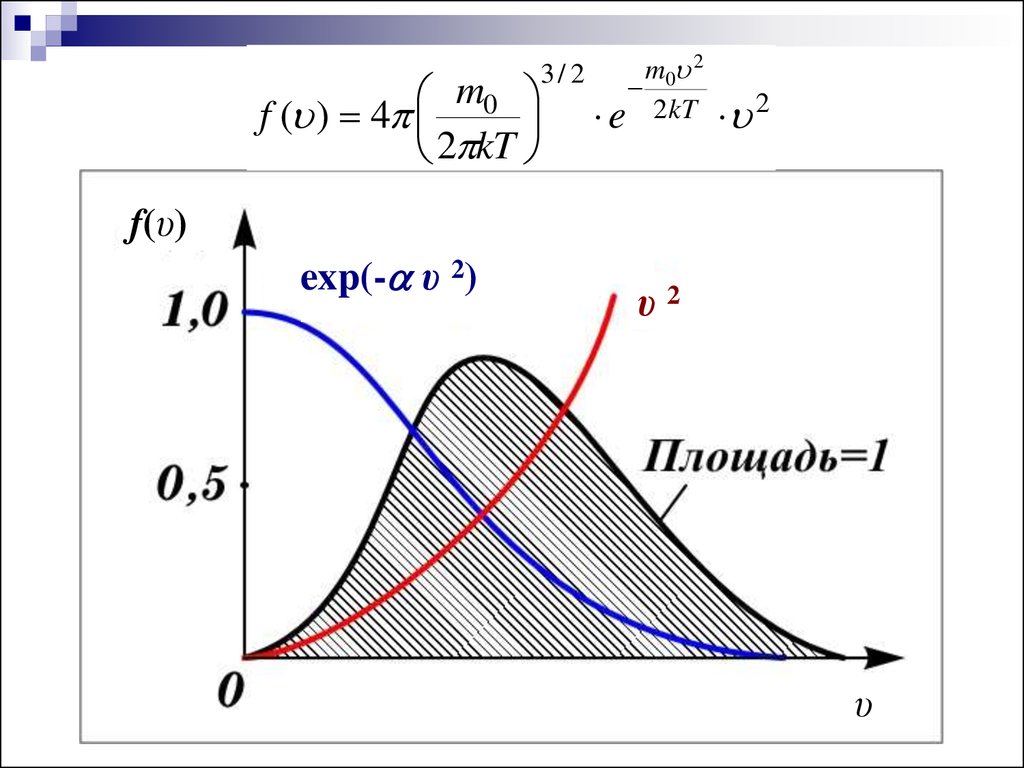
12.

m0
f ( ) 4
2 kT
3/ 2
m0 2
e 2 kT
2
f(υ)
exp(- υ 2)
υ2
υ

13.

3/ 2
m0 2
e 2 kT
m0
2
f ( ) 4
2 kT
Основные свойства функции распределения
1. При υ=0 и υ=∞ f (υ)=0
– очень большие и маленькие
скорости маловероятны
2. Существует υвер – наиболее вероятная скорость, с
которой
движется большинство
молекул. Ей
соответствует максимум функции распределения
Максвелла.
2kT
2 RT
df ( )
вер
0
m0
d

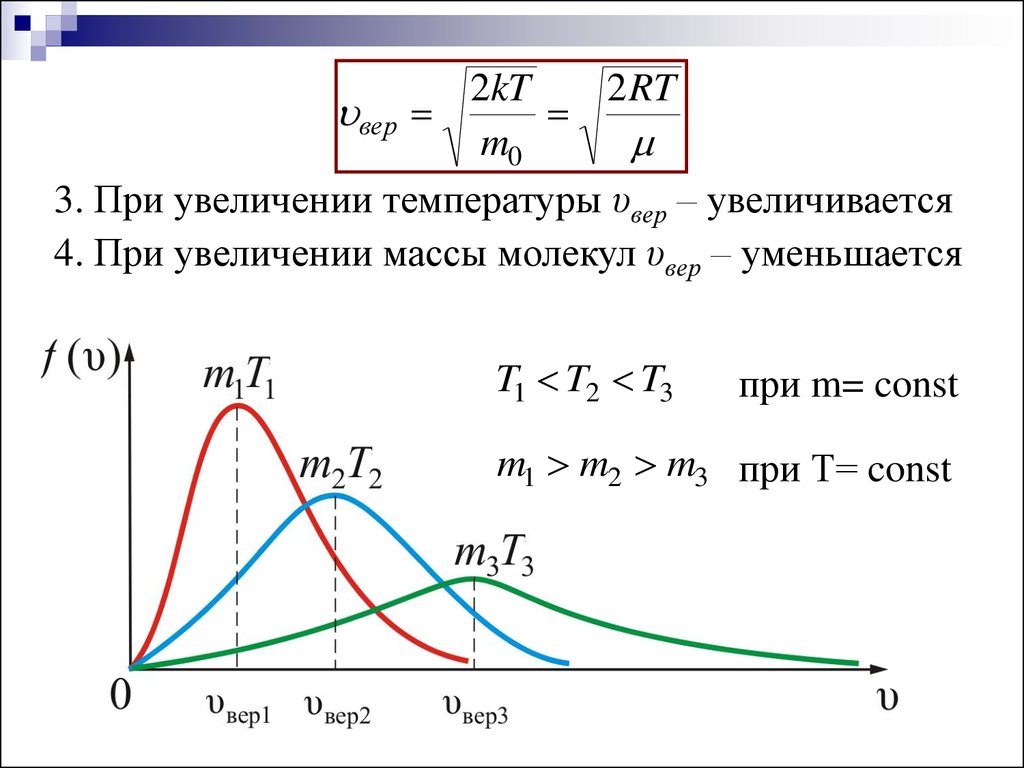
14.

2kT
2 RT
вер
m0
3. При увеличении температуры υвер – увеличивается
4. При увеличении массы молекул υвер – уменьшается
T1 T2 T3
при m= const
m1 m2 m3 при Т= const

15.

16.

ПРИМЕНЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
1. Нахождение относительного числа молекул со
скоростями от υ1 до υ2
Обозначим:
dN– число молекул со скоростями от υ до υ +dυ
N – общее число молекул газа в данном объеме
dN
f ( ) d - вероятность того,
что скорость данной
N
молекулы лежит в
интервале скоростей
от υ до υ + dυ.

17.

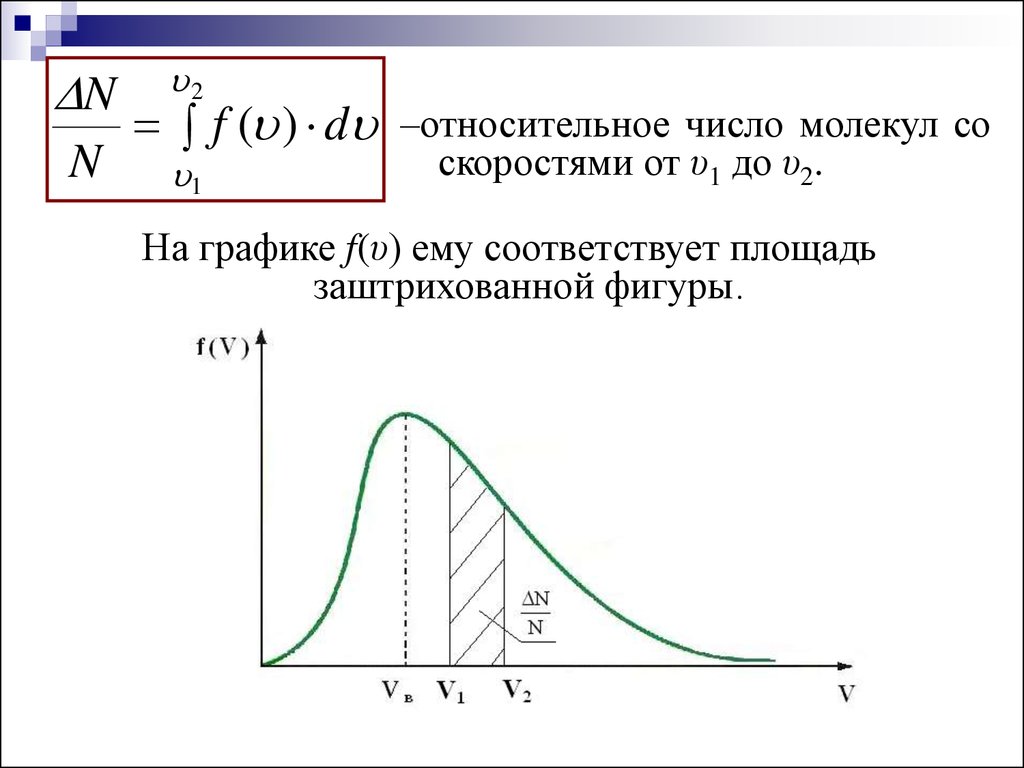
N
N
2
f ( ) d –относительное число молекул со
1
скоростями от υ1 до υ2.
На графике f(υ) ему соответствует площадь
заштрихованной фигуры.

18.

2. Нахождение средней скорости
N молекул υср
По определению:
i
i 1
N
Разобьем весь интервал возможных скоростей (от
нуля до бесконечности) на элементарные интервалы dυ.
dN – число молекул, скорости которых лежат в
пределах одного из таких интервалов.
Так как dυ - элементарный интервал, то можно
считать, что все скорости, принадлежащие этому
интервалу, одинаковы и равны υ.
dN
f ( )
N d
dN Nf ( )d

19.

dN N f ( ) d
dN - сумма скоростей молекул, скорости которых
лежат в интервале от υ до υ + Δ υ.
Тогда сумма скоростей всех молекул:
N
N
i 1
0
i dN
f Nd
0
N
m0
4
2 kT
3/ 2
f ( ) N d
0
m0
4
2 kT
3k 2T 2
2
m
0
2
1
m
3
0
d
exp
0
2 kT
3/ 2
8kT
8 RT
m0

20.

3. Нахождение средней кинетической энергии молекул
1
3
Ek
E dN E f ( )d kT
N
2
0
вер
0
3
Ek kT
2
2kT
– наиболее вероятная скорость
m0
3kT
– средняя квадратичная скорость
кв
m0
8kT
– средняя арифмети
m0
ческая скорость
кв
1.22
вер
ср
1.13
вер

21.

2. Распределение Больцмана
(для описания распределения молекул по высоте в
гравитационном поле Земли)

22. 2. Распределение Больцмана

ИДЕАЛЬНЫЙ ГАЗ В ОДНОРОДНОМ ПОЛЕ ТЯГОТЕНИЯ
БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
Барометрическая формула выражает зависимость
атмосферного давления от высоты над уровнем моря.
Атмосферное давление на высоте h
h
обусловлено весом вышележащих слоев
газа.
Р - давление на высоте h
h+dh
h
0
P+dP
P
(P + dP) - давление на высоте (h + dh)
dh > 0
dP < 0
(на большей высоте давление меньше)
dP gdh – изменение давления с
увеличением высоты
– плотность газа
g – ускорение свободного падения

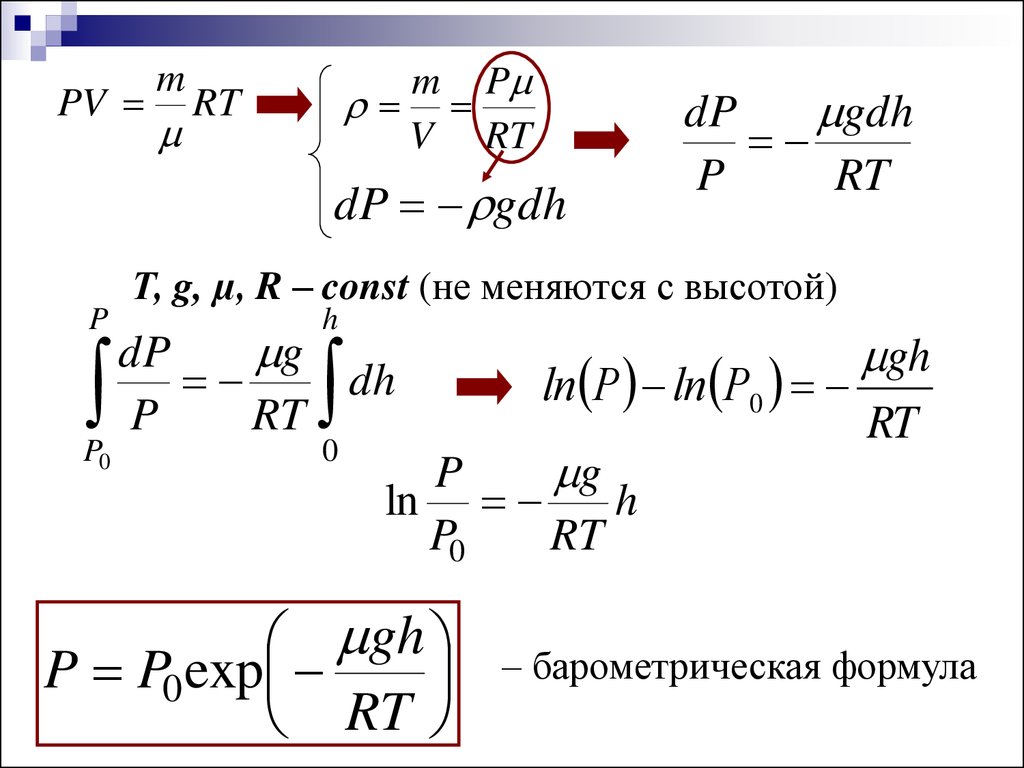
23.

PV
m
m P
V RT
RT
dP gdh
P
P0
dP
gdh
P
RT
Т, g, µ, R – const (не меняются с высотой)
h
dP
g
dh
P
RT
0
gh
ln Р ln Р0
RT
g
P
ln
h
P0
RT
gh
P P0 exp
RT
– барометрическая формула

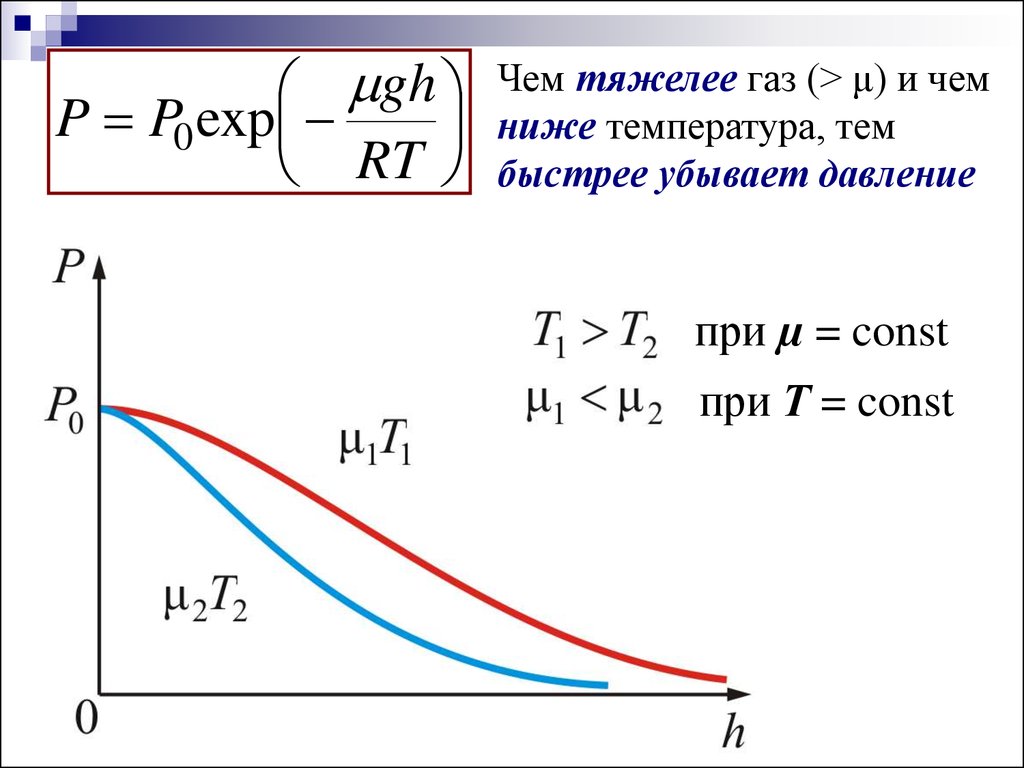
24.

gh
P P0 exp
RT
Чем тяжелее газ (> μ) и чем
ниже температура, тем
быстрее убывает давление
при µ = const
при Т = const

25.

РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА
Распределение Больцмана определяет
распределение частиц в силовом поле в
условиях теплового равновесия.
P nkT
P0 n0kT
Людвиг Больцман
(1844–1906)
P0 и n0 – давление и концентрация газа
на нулевой высоте, P и n – на высоте h
gh
gh
P P0 exp
nkT n0 kT exp
RT
RT
m0 N A
m0 gh
m0 N A gh
n n0 exp
n n0 exp
kT
kN AT
R N Ak
распределение Больцмана в поле силы тяжести

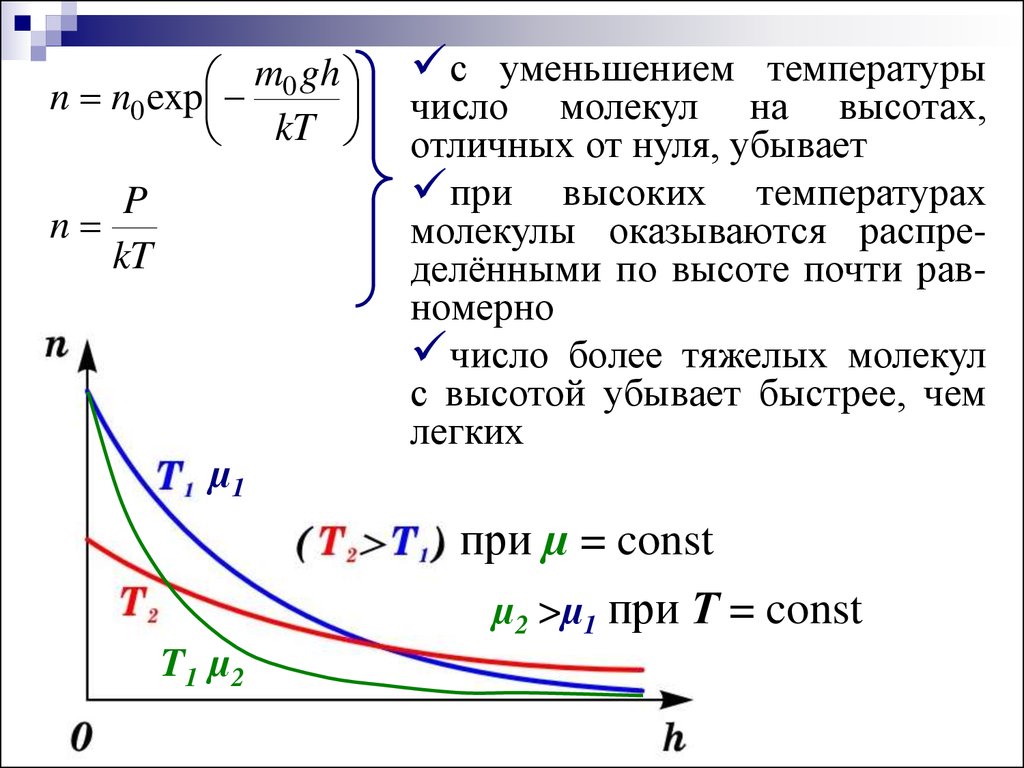
26.

m0 gh
n n0 exp
kT
P
n
kT
µ1
с уменьшением температуры
число молекул на высотах,
отличных от нуля, убывает
при высоких температурах
молекулы оказываются распределёнными по высоте почти равномерно
число более тяжелых молекул
с высотой убывает быстрее, чем
легких
при µ = const
µ2 >µ1 при Т = const
T1 µ2

27.

m0 gh
n n0 exp
kT
Еп = m0gh – потенциальная энергия одной молекулы в
поле тяготения на высоте h от уровня моря, тогда
n0 – концентрация частиц в том месте, где Eп = 0
En
n n0 exp – распределение Больцмана характе kT ризует распределение частиц по значениям потенциальной энергии
Распределение справедливо в любом потенциальном
поле сил для совокупности любых частиц, находящихся
в состоянии хаотического теплового движения.
Оно устанавливается в результате совместного
действия потенциального поля и теплового движения.

28.

29.

ЯВЛЕНИЯ ПЕРЕНОСА в
неравновесных системах

30. ЯВЛЕНИЯ ПЕРЕНОСА в неравновесных системах

1. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА
МОЛЕКУЛ И СРЕДНЕЕ ЧИСЛО СТОЛКНОВЕНИЙ
Средняя длина свободного пробега молекул < > –
это среднее расстояние, которое молекула проходит
между двумя последовательными соударениями.
λ1
λ2
λ3
λ4

31.

Эффективный диаметр молекулы dэф – минимальное расстояние, на которое сближаются центры молекул
при их соударении.
определяется природой самого
dэф
σэф
газа (увеличивается при увеличении размеров молекул)
зависит от скорости сталкивающихся молекул, т.е. от температуры (уменьшается при увеличении температуры)
Эффективное сечение молекул σэф – площадь круга с
радиусом, равным эффективному диаметру (площадь в
которую не может проникнуть центр любой другой
молекулы).
2
эф d эф

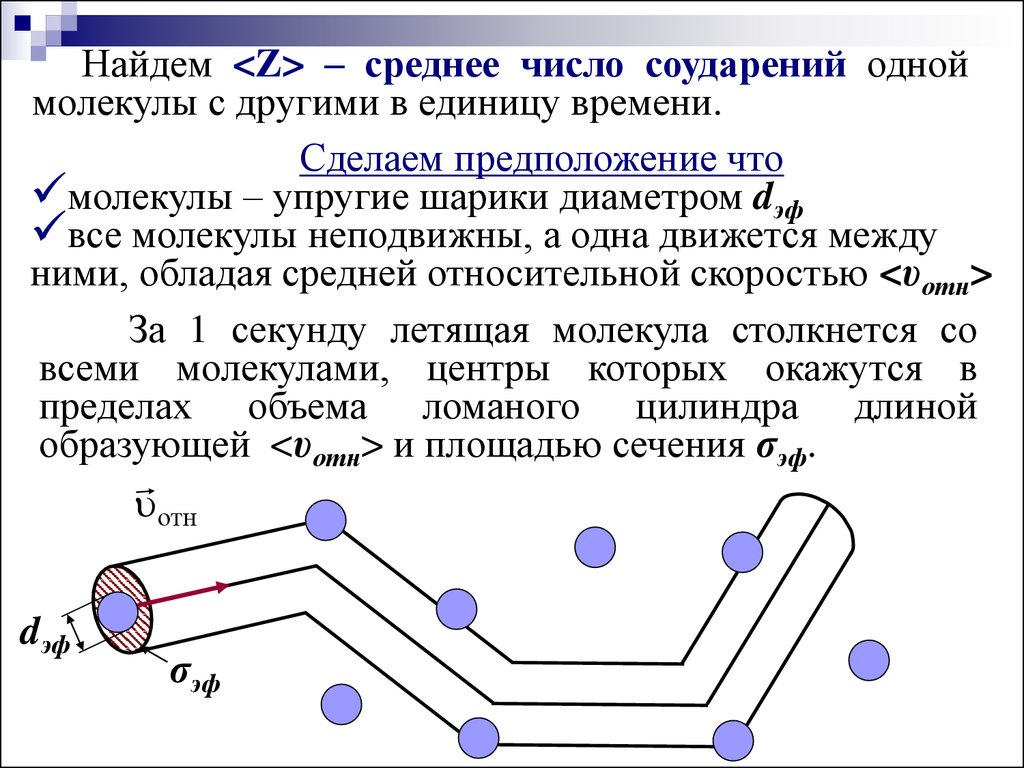
32.

Найдем <Z> – среднее число соударений одной
молекулы с другими в единицу времени.
Сделаем предположение что
молекулы – упругие шарики диаметром dэф
все молекулы неподвижны, а одна движется между
ними, обладая средней относительной скоростью <υотн>
За 1 секунду летящая молекула столкнется со
всеми молекулами, центры которых окажутся в
пределах объема ломаного цилиндра длиной
образующей <υотн> и площадью сечения σэф.
отн
dэф
σэф

33.

1
2
Z
2 d эф
n
P
n
kT
kT
2
2 d эф
P
При нормальных условиях (Т = 300 К и Р = 105 Па)
для газа с dэф = 3∙10 – 10 м (азот):
1,38 10 23 300
7
10
м
10 2
5
2 3,14 (3 10 ) 10

34.

kT
2
2 d эф
P
1.V = const => P/T= const, но диаметр слабо уменьшается с ростом температуры и < > увеличивается.
2. Р=const. С ростом температуры < > увеличивается
практически пропорционально температуре.
3. Т=const. С увеличением давления < > уменьшается.
Если < > сравнима или больше размеров сосуда L в
котором находится газ, то такое состояние газа
называется вакуумом.
ВАКУУМ
Средний
< > ≤ L
Высокий
< > > L
Сверхвысокий
< > >> L

35.

2. ЯВЛЕНИЯ ПЕРЕНОСА
Явления переноса – круг явлений в термодинамически неравновесных системах, в процессе которых
происходит выравнивание параметров макроскопической системы, при этом система стремится к состоянию равновесия.
Процессы выравнивания сопровождаются направленным переносом ряда физических величин (массы,
энергии, импульса и т.д.) и поэтому называются
явлениями переноса.
К явлениям переноса в газах относятся
А) диффузия,
Б) внутреннее трение (вязкость),
В) теплопроводность.

36.

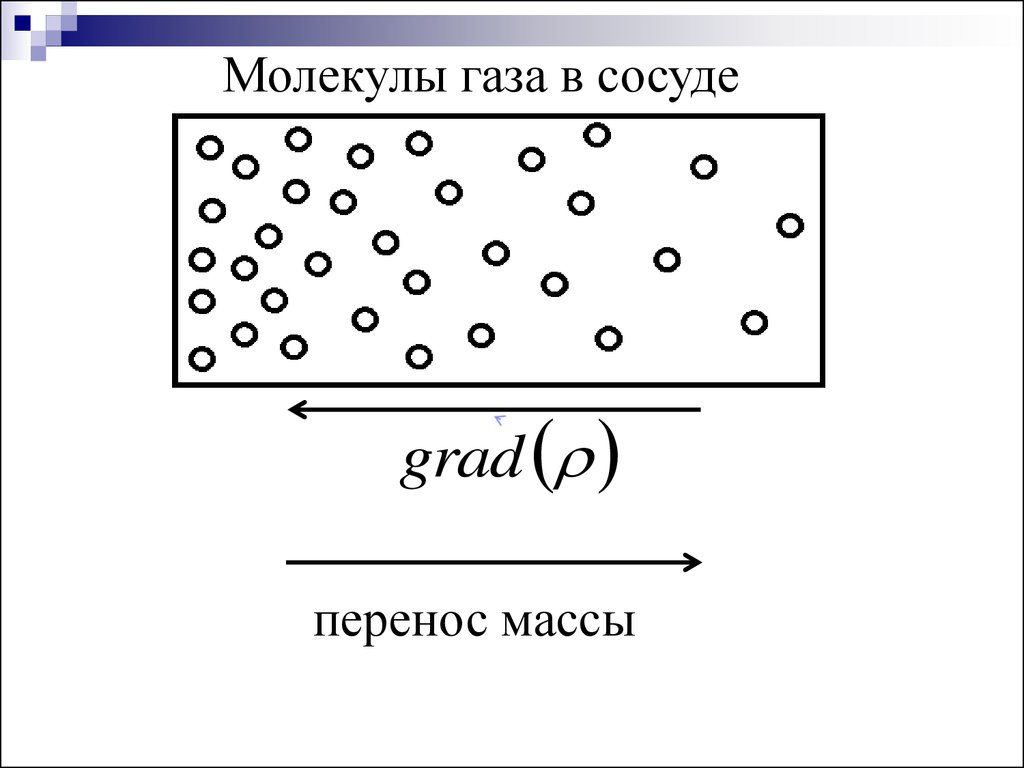
А) Диффузия – процесс переноса массы
вещества молекулами за счет их хаотического
движения при наличии градиента плотности (или
концентрации молекул).
Диффузия имеет место в газах, жидкостях и твердых телах

37.

При диффузии масса переносится из мест с большей
концентрацией в места с меньшей концентрацией, что
приводит к ее равномерному распределению по
занимаемому объему.
Математически диффузия описывается законом Фика
d
dm D dS dt
dr
Масса вещества dm, переносимая молекулами за
время dt через площадку dS , расположенную
перпендикулярно направлению переноса (оси r),
прямо пропорциональна
проекции градиента
d
плотности
на направление быстрейшего возdr
растания плотности.

38.

Молекулы газа в сосуде
grad
перенос массы

39.

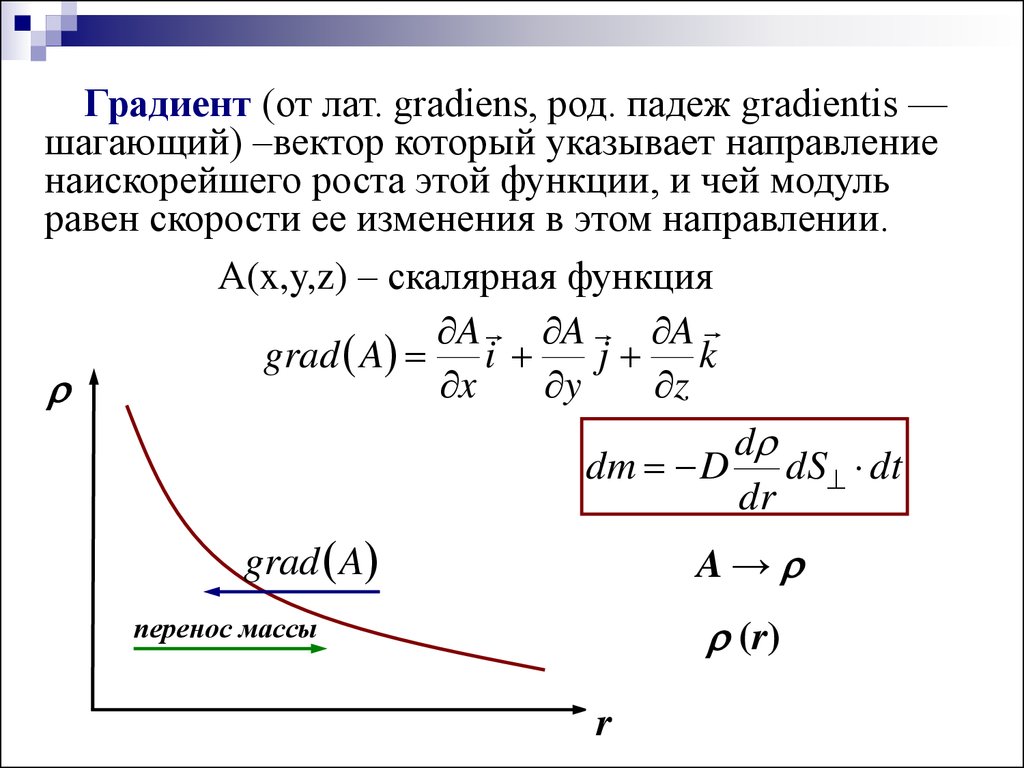
Градиент (от лат. gradiens, род. падеж gradientis —
шагающий) –вектор который указывает направление
наискорейшего роста этой функции, и чей модуль
равен скорости ее изменения в этом направлении.
А(x,y,z) – скалярная функция
A A A
grad A i
j k
x
y
z
A
d
dm D dS dt
dr
grad A
A→
(r)
перенос массы
rx

40.

d
dm D dS dt
dr
Знак «–» показывает, что перенос массы происходит
в направлении убывания плотности (обратно
направлению градиента плотности).
dm –диффузионный поток через единицу площади
J
dS dt в единицу времени (плотность потока массы)
d
D – коэффициент диффузии
J D
dr
1
Согласно кинетической теории газов: D
3
<υ> – средняя скорость молекул
< > – средняя длина свободного пробега молекул
м2
D
с

41.

Диффузия через пористую перегородку

42.

Прибор Анселя

43. Диффузия через пористую перегородку

Б) Внутреннее трение (вязкость) – возникновение
силы внутреннего трения при взаимодействии между
слоями газа (жидкости), движущимися с различными
скоростями.
υ
υ=0

44. Прибор Анселя

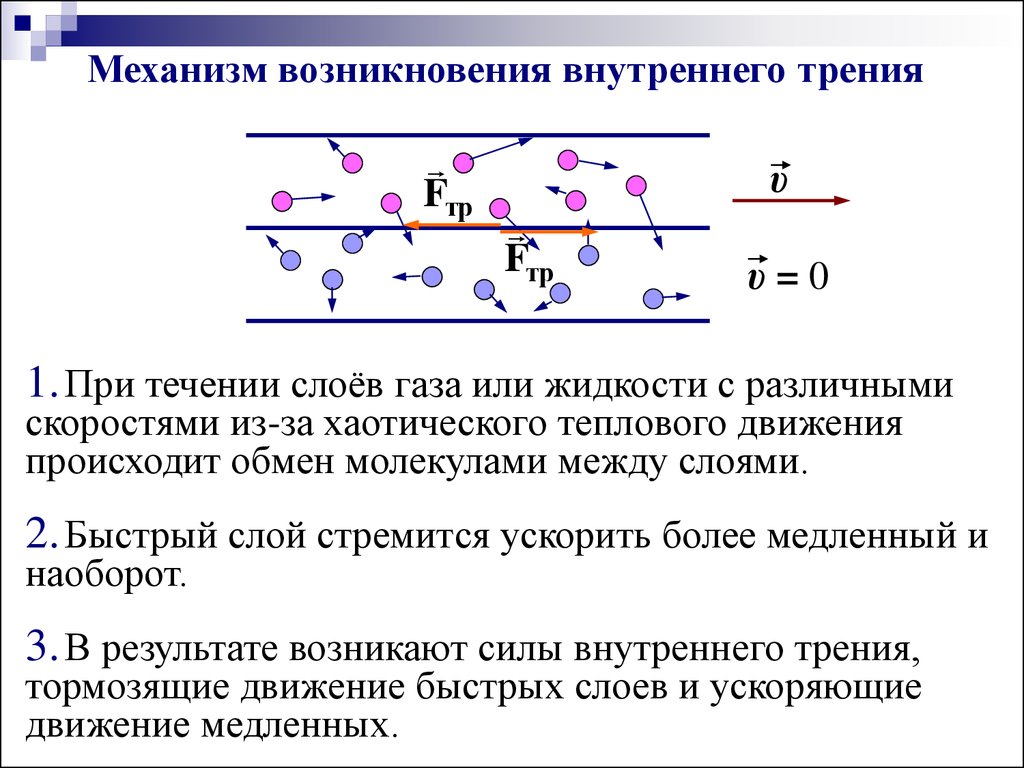
Механизм возникновения внутреннего трения
Fтр
υ
Fтр
υ=0
1. При течении слоёв газа или жидкости с различными
скоростями из-за хаотического теплового движения
происходит обмен молекулами между слоями.
2. Быстрый слой стремится ускорить более медленный и
наоборот.
3. В результате возникают силы внутреннего трения,
тормозящие движение быстрых слоев и ускоряющие
движение медленных.

45.

Вязкое трение в газе (жидкости) – это результат
переноса импульса направленного движения слоев газа
за счет хаотического движения при наличии в газе
(жидкости)
градиента
скорости
направленного
движения.
Внутреннее трение подчиняется закону Ньютона:
d
dp dS dt
dr
Импульс направленного движения слоев газа dp,
перенесенный молекулами за время dt через площадку
dS , расположенную перпендикулярно направлению
переноса (оси r), прямо пропорционален проекции
d
градиента скорости направленного движения
на
dr
направление быстрейшего возрастания скорости.

46.

d
dp dS dt
dr
Знак «–» означает, что направление переноса
импульса и направление возрастания скорости
противоположны.
dp
d
F
Fтр dS – сила терния действующая
dt
dr
на площадку dS на границе
раздела параллельно движущихся слоев
1
– динамическая вязкость
(коэффициент вязкости)
3
ρ – плотность газа
кг
Па с
м с

47.

48.

В) Теплопроводность – процесс выравнивания
температуры, сопровождающийся направленным
переносом тепловой энергии из более нагретых
слоев в менее нагретые за счет хаотического
движения молекул.

49.

Механизм возникновения теплопроводности
T1
T2
1. Хаотично двигаясь, молекулы будут
переходить из одного слоя газа
(жидкости) в другой, перенося с собой
энергию.
2. Это движение молекул приводит к
перемешиванию молекул, имеющих
различную кинетическую энергию.
3. В результате кинетическая энергия
T2> T1
быстрых слоев уменьшается, а
медленных – увеличивается.

50.

При теплопроводности энергия в виде тепла
переносится из мест с большей температурой в места с
меньшей температурой, что приводит к ее
вырвниванию.
Процесс теплопроводности описывается законом Фурье:
dT
Q dS dt
dr
Элементарное количество тепла Q, переносимое
в стационарном процессе теплопроводности за время
dt через площадку dS , перпендикулярную
направлению переноса, прямо пропорционально
dÒ
проекции градиента температуры
на направление
dr
быстрейшего возрастания температуры.

51.

dT
Q dS dt
dr
Знак «–» показывает, что при теплопроводности
энергия
переносится
в
сторону
убывания
температуры.
Q
– тепло переносимое через единицу площади в
q
dS dt единицу времени (тепловой поток)
dT
q
– коэффициент теплопроводности
dr
1
Согласно кинетической теории газов: cV V
3
cV – удельная теплоемкость газа при постоянном объеме
кг м Вт
3
с К м К

52.

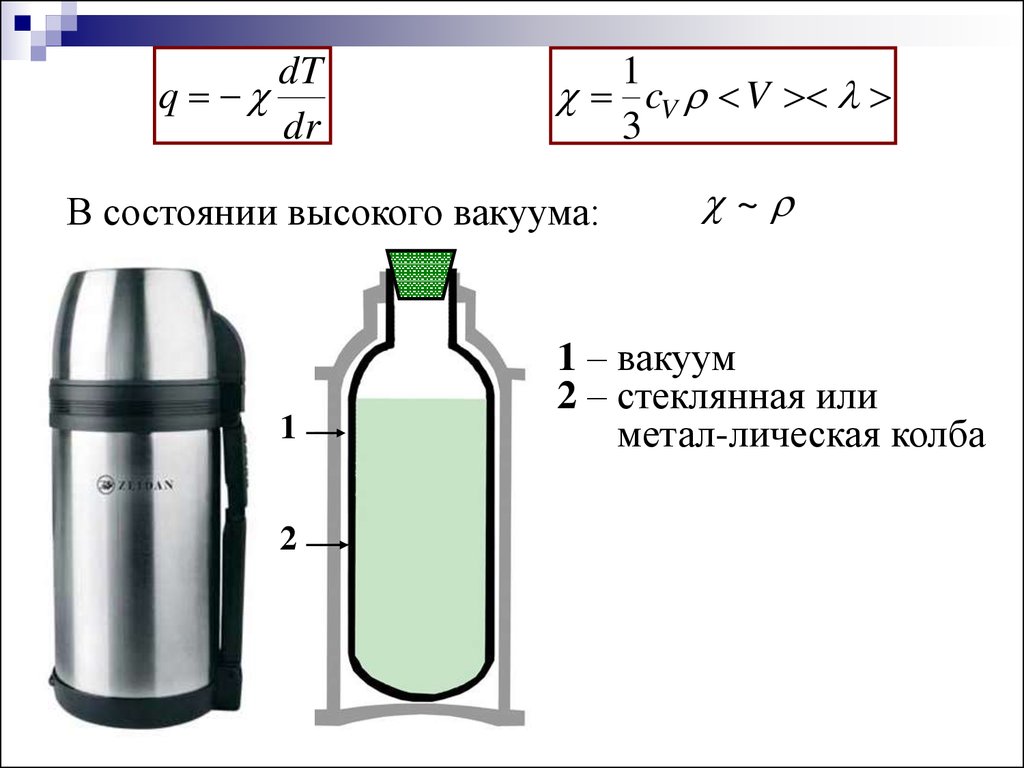
dT
q
dr
1
cV V
3
В состоянии высокого вакуума:
1
2
~
1 – вакуум
2 – стеклянная или
метал-лическая колба

53.

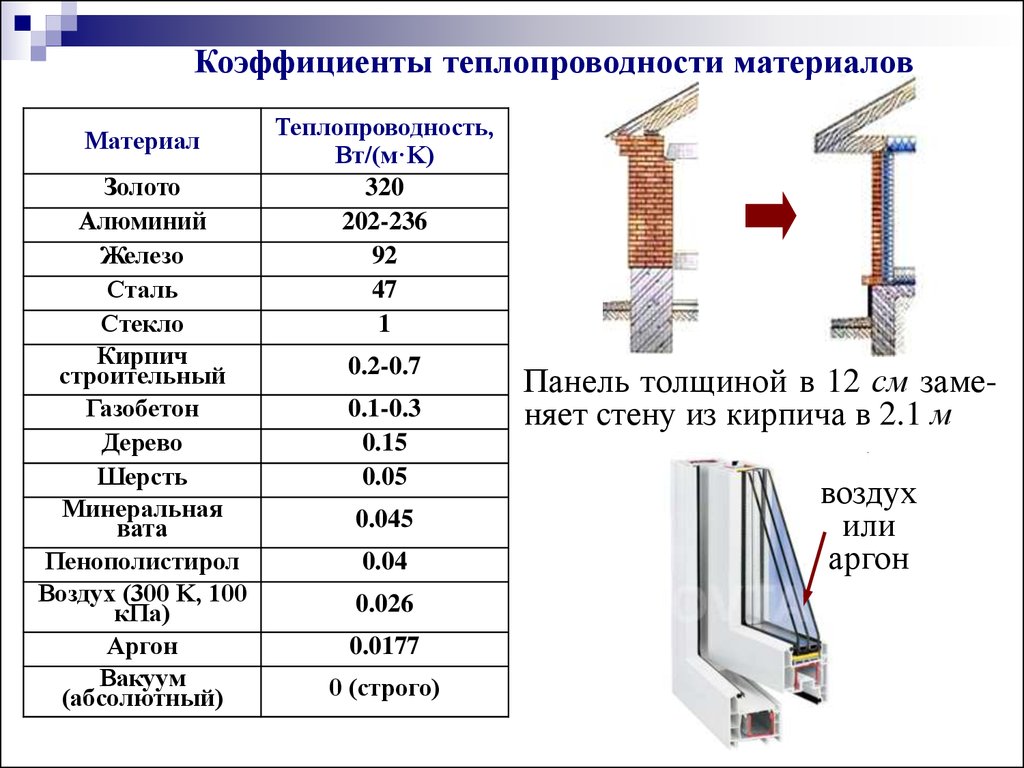
Коэффициенты теплопроводности материалов
Материал
Золото
Алюминий
Железо
Сталь
Стекло
Кирпич
строительный
Газобетон
Дерево
Шерсть
Минеральная
вата
Пенополистирол
Воздух (300 K, 100
кПа)
Аргон
Вакуум
(абсолютный)
Теплопроводность,
Вт/(м·K)
320
202-236
92
47
1
0.2-0.7
0.1-0.3
0.15
0.05
0.045
0.04
0.026
0.0177
0 (строго)
Панель толщиной в 12 см заменяет стену из кирпича в 2.1 м
воздух
или
аргон

54.

Теплопроводность газов

55.

L=1 м
T2=+25°C
T1=-25°C
q
Q 25 40 24 60 60 86.4 МДж
dT
q
dr
0.5 Вт / м К
dT T
dr r
T 25 - - 25 50 C
T 50 K r L 1 ì
T
K
50
r
м
Дж
q 0.5 50 25 2
м с
S=40 м2 t=24 часа
Q q S t
Необходимо сжечь
6.6 кг дров

56. Теплопроводность газов

Связь коэффициентов переноса с величинами,
характеризующими движение молекул газа
1
1
1
cV
D
3
3
3
D
8kT
m0
T T
D~
Р
D cV
kT
2
2 d эф Р
~ T
cV
P
RT
iR
cV
2
~ T