Похожие презентации:
Поглощение лазерного излучения в металлах и полупроводниках
1. Лекция 2. поглощение лазерного излучения в металлах и полупроводниках
ЛЕКЦИЯ 2. ПОГЛОЩЕНИЕЛАЗЕРНОГО ИЗЛУЧЕНИЯ В
МЕТАЛЛАХ И ПОЛУПРОВОДНИКАХ
2. Комплексная диэлектрическая проницаемость
КОМПЛЕКСНАЯ ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬВолновое уравнение для проводящей среды при ρе = 0
2E
2E
E
0
r
0
r
0
r
0
x 2
t 2
t
σ – проводимость металла
εr, μr – диэлектрическая и магнитная проницаемости
Для гармонических полей вида E (t ) E exp i t
2 E 2
i
E 0
r r
x 2
c2
0
c
1
0 0
- скорость света в вакууме
В случае диэлектрика σ = 0, и волновое уравнение имеет стандартный вид
2 E 2
2 r r E 0
x 2
c
Уравнения для проводящей и непроводящей сред формально совпадут если ввести
комплексную диэлектрическую проницаемость .
i
0
- комплексная диэлектрическая проницаемость
2
r
3. Поглощение электромагнитных волн в металле
ПОГЛОЩЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В МЕТАЛЛЕРешение уравнения для амплитуды поля в проводящей среде будем искать в виде:
E E0 exp ikx
После подстановки получим: k
2
2
c2
2
c2
n 2 (здесь принято, что μr = 1)
k k is - комплексное волновое число
n 2 , n n ik p- комплексный показатель преломления (kp – коэффициент экстинкции)
Комплексность волнового числа означает, что амплитуда поля убывает по
экспоненциальному закону.
для реальных
металлов δ<<λ !!
3
Действительно E0 exp i k is x E0 exp sx exp ikx
k p
s
c
Для интенсивности:
2 k p
I exp x ,
c
1
- глубина проникновения излучения, рассто
яние на котором интенсивность излучения спадает
в e раз.
4. Отражение электромагнитной волны от границы металл-воздух
ОТРАЖЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ ОТ ГРАНИЦЫМЕТАЛЛ-ВОЗДУХ
B
для плоской,
t
линейно поляризованной волны вида
Из уравнения rotE
E y E0 exp i t kx , Bz B0 exp i t kx ,
можно получить соотношение для амплитуд:
kE0 B0 или nE0 cB0 .
(отсюда также следует, что отношение сил,
действующих на заряд со стороны
магнитного и электрического поля порядка
v/c, где v – скорость частицы).
Для отраженной волны:
Для прошедшей волны:
E yi E0i exp i t x
c
E yr E0r exp i t x
c
n
E yt E0t exp i t
x
c
Bzi B0i exp i t x
c
Bzr B0r exp i t x
c
n
Bzt B0t exp i t
x
c
4
Для падающей волны:
5. Коэффициент отражения. Поглощательная способность
КОЭФФИЦИЕНТ ОТРАЖЕНИЯ. ПОГЛОЩАТЕЛЬНАЯСПОСОБНОСТЬ
На границе металл-воздух должны выполняться условия
тангенциальных компонент электрических и магнитных полей.
непрерывности
E0i E0r E0t
E0i E0r nE0t
E0r
Решая эту систему относительно r i ,
E0
получим r
Отношение интенсивностей отраженной
коэффициентом отражения металла R.
R
E0r
2
i 2
0
и
n 1
.
n 1
падающей
волн
называют
n 1 k p2
R
2
n 1 k p2
2
r
E
2
Всегда имеет место соотношение R + A + T = 1. Для металлов T = 0, поэтому
поглощательная способность равна:
A
4n
n 1
2
k p2
Поглощательная способность определяет долю
энергии электромагнитной волны, поглощенной
средой.
5
A 1 R
6. теория Друде-Лоренца
ТЕОРИЯ ДРУДЕ-ЛОРЕНЦАНа практике важно знать частотные и температурные зависимости A(ω, T) и α(ω, T),
т.е. n(ω, T) и kp(ω, T) для металлов.
Для определения зависимостей n(ω, T) и kp(ω, T) будем использовать классическую
модель Друде-Лоренца. В модели Друде для рассмотрения электронного газа в
металлах практически без изменений применяются методы кинетической теории
разреженных газов.
Основные положения теории Друде:
6
1. В интервале между столкновениями не учитывается взаимодействие электрона
с другими электронами и ионами. (приближение свободных и независимых
электронов).
2. Столкновения - внезапные события, меняющие скорость электрона.
Столкновения поддерживают локальное термодинамическое равновесие:
скорость электрона не связана со скоростью до столкновения, её величина
соответствует температуре области где произошло столкновение.
3. Для электрона вероятность испытать столкновение за время dt равна dt/τ. (τ –
время свободного пробега).
7. Связь проводимости с микро-характеристиками металла
СВЯЗЬ ПРОВОДИМОСТИ С МИКРО-ХАРАКТЕРИСТИКАМИМЕТАЛЛА
Можно показать, что изменение импульса, приходящегося на один электрон, во
внешнем переменном электрическом поле подчиняется уравнению:
dp
p
eE (t )
dt
- эффект столкновений отдельных электронов сводится к
введению дополнительного члена соответствующего трению.
Для гармонических воздействий E y (t ) E0 exp i t будем искать решение в виде:
После подстановки получаем:
p y (t )
Для плотности тока справедливо:
nee 2
Соответственно ( )
(1 i )me
eE y (t )
1
i
je (t )
neep y (t )
me
при ω = 0
E y (t )
nee 2
0
me
7
p y (t ) p0 exp i t .
8. Дисперсия комплексной диэлектрической проницаемости
ДИСПЕРСИЯ КОМПЛЕКСНОЙ ДИЭЛЕКТРИЧЕСКОЙПРОНИЦАЕМОСТИ
( ) r ( )
i ( )
0
Выделяя вещественную и мнимую части в выражении для комплексной
диэлектрической проницаемости, получим:
p2
p2
Re r 2
Im
2
( 2 2 )
1
nee 2
1013 1014 с 1
плазменная
частота
p
0 me
Для металлов ne
1022 1023 см 3 соответственно p
- частота столкновений
5 1015 1016 c 1
8
Параметры γ и ωp играют роль граничных параметров, определяющих
дисперсионные зависимости оптических свойств металлов.
9. Дисперсия комплексного показателя преломления
ДИСПЕРСИЯ КОМПЛЕКСНОГО ПОКАЗАТЕЛЯПРЕЛОМЛЕНИЯ
n2
p2
2
p
n 2 k p2 1 2
2
nk
p
2
2 2
2
2
b можно получить дисперсионные зависимость n и kp в виде:
1
n( )
2
1
k p ( )
2
2
b
b
1
b 1
2
2
b
b
1
b 1
2
9
Обозначив
p2
(здесь принято εr = 1)
10. Частотные зависимости оптических свойств металла
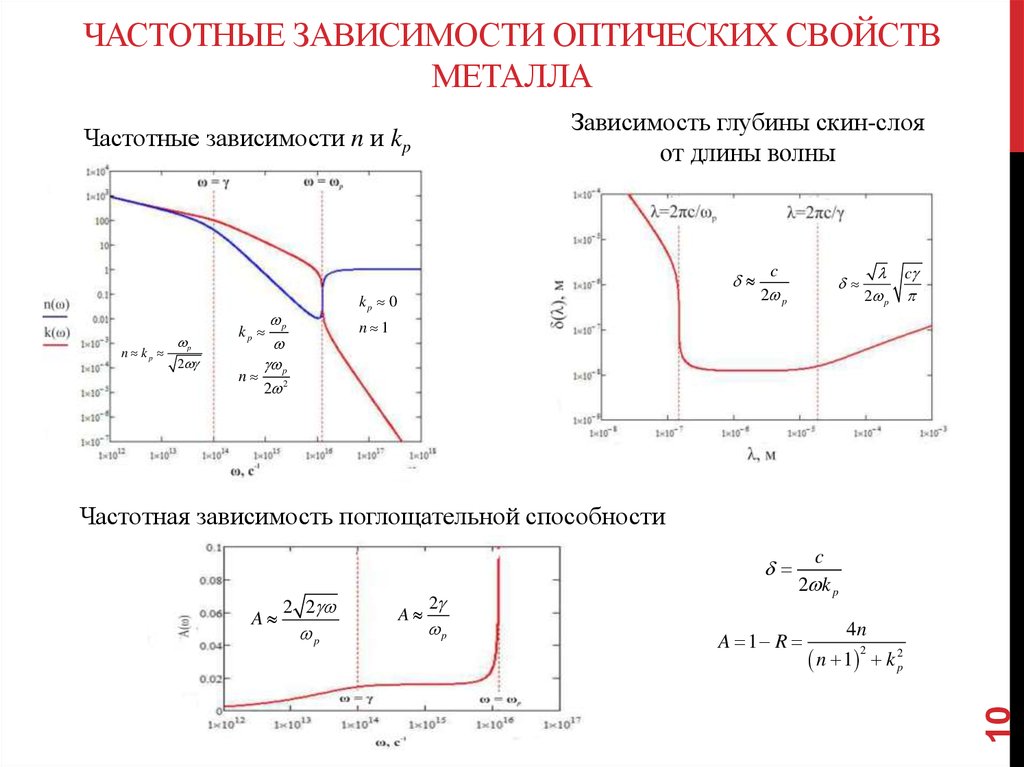
ЧАСТОТНЫЕ ЗАВИСИМОСТИ ОПТИЧЕСКИХ СВОЙСТВМЕТАЛЛА
Зависимость глубины скин-слоя
от длины волны
Частотные зависимости n и kp
n kp
p
2
kp 0
p
n p2
2
c
2 p
c
2 p
n 1
kp
Частотная зависимость поглощательной способности
A
2 2
p
A
2
p
c
2 k p
A 1 R
4n
n 1
2
k p2
10
11. Температурная зависимость поглощательной способности
ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ПОГЛОЩАТЕЛЬНОЙСПОСОБНОСТИ
проводимость металла зависит от
температуры
оптические характеристики
также зависят от температуры
1
Известно, что при T > TD (TD – температура Дебая) T 0 T .
Если p , то A
2
p
и можно записать A T A0 T T0 .
Параметр χ ~ 10-5 – 10-4 K-1 может быть определен по температурным зависимостям
проводимости.
При нагреве на 1000 К температурная добавка к поглощательной способности
может составлять несколько процентов, что может быть существенно, ввиду её
низкого первоначального значения.
11
Таким образом, между нагревом и поглощением излучения имеется
положительная обратная связь, что может приводить к появлению
неустойчивостей в динамике нагрева и снижению порогов повреждения металлов.
12. Влияние связанных электронов на оптические характеристики металлов
ВЛИЯНИЕ СВЯЗАННЫХ ЭЛЕКТРОНОВ НА ОПТИЧЕСКИЕХАРАКТЕРИСТИКИ МЕТАЛЛОВ
В реальных металлах не всегда можно пренебречь вкладом в диэлектрическую
проницаемость от связанных электронов.
Влиянием связанных электронов объясняется цвет металла (медь, золото).
Плотность электронных состояний в меди
медь
золото
серебро
ΔE ~ 2 эВ (620 нм)
ΔE ~ 2.5 эВ
ΔE ~ 4 эВ (310 нм)
12
Разность между потолком d-зоны и уровнем Ферми для некоторых металлов:
13. Аномальный скин-эффект
АНОМАЛЬНЫЙ СКИН-ЭФФЕКТДля проведенного ранее рассмотрения было существенно выполнение закона Ома.
Однако в условиях, когда длина свободного пробега электрона превышает
характерный масштаб на котором существенно меняется поле (т.е. глубину скинслоя), то электрон, двигаясь за время свободного пробега получит добавочную
скорость, которая будет зависеть от напряжённости поля вдоль пути движения.
Значение плотности тока в некоторой точке уже не будет определяться значением
поля в той же точке.
Соответственно:
j E , j f E , x
Более детальный анализ показывает, что
Av
2
p
As
3 vF
p
4 c
Av – объемная поглощательная способность
As – поверхностная поглощательная способность
p – доля диффузно отраженных поверхностью электронов
(0 < p < 1, существенно зависит от шероховатости)
vF - скорость Ферми
Вклад поверхностного поглощения может быть заметен при низких температурах (γ
мало) и для шероховатых поверхностей (большие значения p).
13
A Av As
14. Поглощение излучения в полупроводниках
ПОГЛОЩЕНИЕ ИЗЛУЧЕНИЯ В ПОЛУПРОВОДНИКАХВиды поглощения излучения в полупроводниках:
1. Собственное (межзонное) поглощение света (внутренний фотоэффект).
Eg f Eg , 103 105 cм 1
2. Внутризонное поглощение (поглощение свободными носителями).
Рассматривается аналогично поглощению свободными электронами в металлах
3. Примесное поглощение
Eg , 10 см 1
4. Решеточное поглощение
Излучение взаимодействует непосредственно с ионами полупроводника.
14
103 см 1
15. Электронные переходы в полупроводнике при лазерном возбуждении
ЭЛЕКТРОННЫЕ ПЕРЕХОДЫ В ПОЛУПРОВОДНИКЕ ПРИЛАЗЕРНОМ ВОЗБУЖДЕНИИ
15
Первоначально в результате поглощения квантов излучения происходит генерация
Электрон-дырочных пар, имеющих неравновесное распределение по энергиям.
Процессы внутризонной релаксации приводящие к формированию равновесного
распределения (электрон-электронные столкновения, τ ~ 10-14 с), и выравниванию
Температуры носителей и решетки (электрон-фононное взаимодействие, τ ~ 10-12 с).
16. Электронные переходы в полупроводнике при лазерном возбуждении
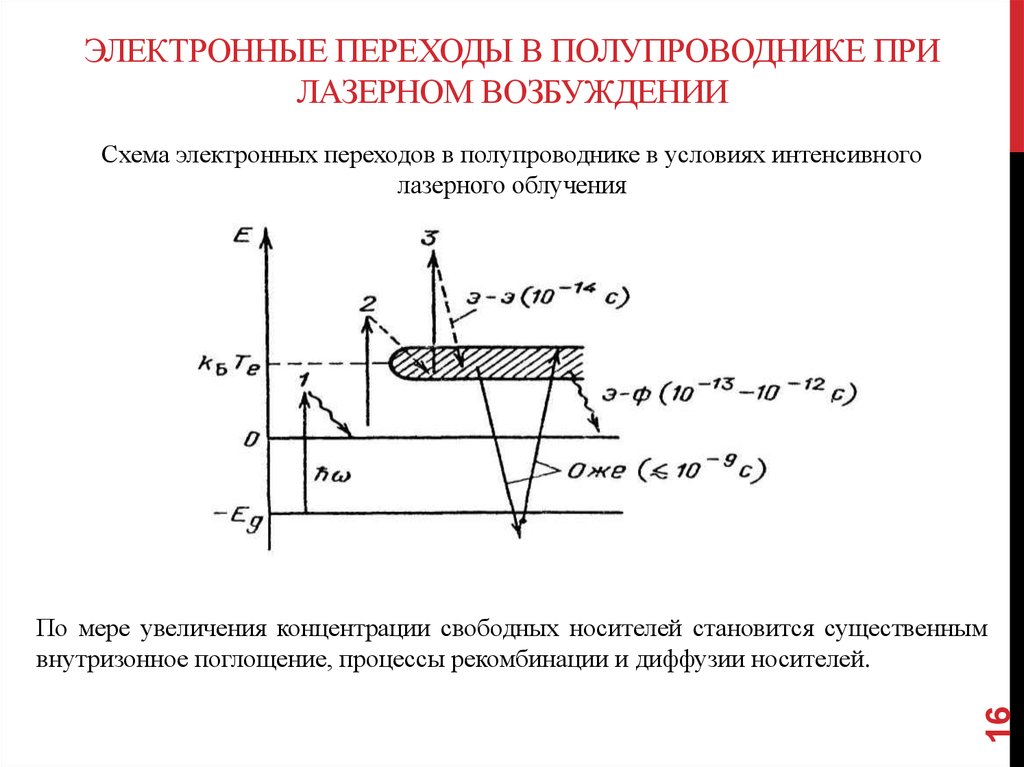
ЭЛЕКТРОННЫЕ ПЕРЕХОДЫ В ПОЛУПРОВОДНИКЕ ПРИЛАЗЕРНОМ ВОЗБУЖДЕНИИ
Схема электронных переходов в полупроводнике в условиях интенсивного
лазерного облучения
16
По мере увеличения концентрации свободных носителей становится существенным
внутризонное поглощение, процессы рекомбинации и диффузии носителей.
17. Процессы рекомбинации
ПРОЦЕССЫ РЕКОМБИНАЦИИВиды рекомбинационных процессов:
1. Излучательная рекомбинация
В результате излучаются световые кванты с энергией ~ Eg.
ne
2 ne2 , 2 10 15 10 20 см3с 1
t
2. Безызлучательная рекомбинация
Энергия ~ Eg передается решетке.
ne
1ne , 1 10 10 9 с 1
t
3. Ударная (Оже) рекомбинация
Энергия, высвобождающаяся при рекомбинации передается другому носителю,
который рассеивает ее впоследствии при взаимодействии с колебаниями
решетки.
ne
3ne3 , 3 10 27 10 33 см 6с 1
t
17
В полупроводниках имеются 2 механизма перевода поглощенной энергии в тепло,
имеющих различный временной масштаб:
1. Быстрые τ ~ 10-13 - 10-12 с (электрон-фононное взаимодействие)
2. Медленные τ ~ 10-9 - 10-2 с (безызлучательная рекомбинация)
18. Межзонное поглощение. Прямые переходы
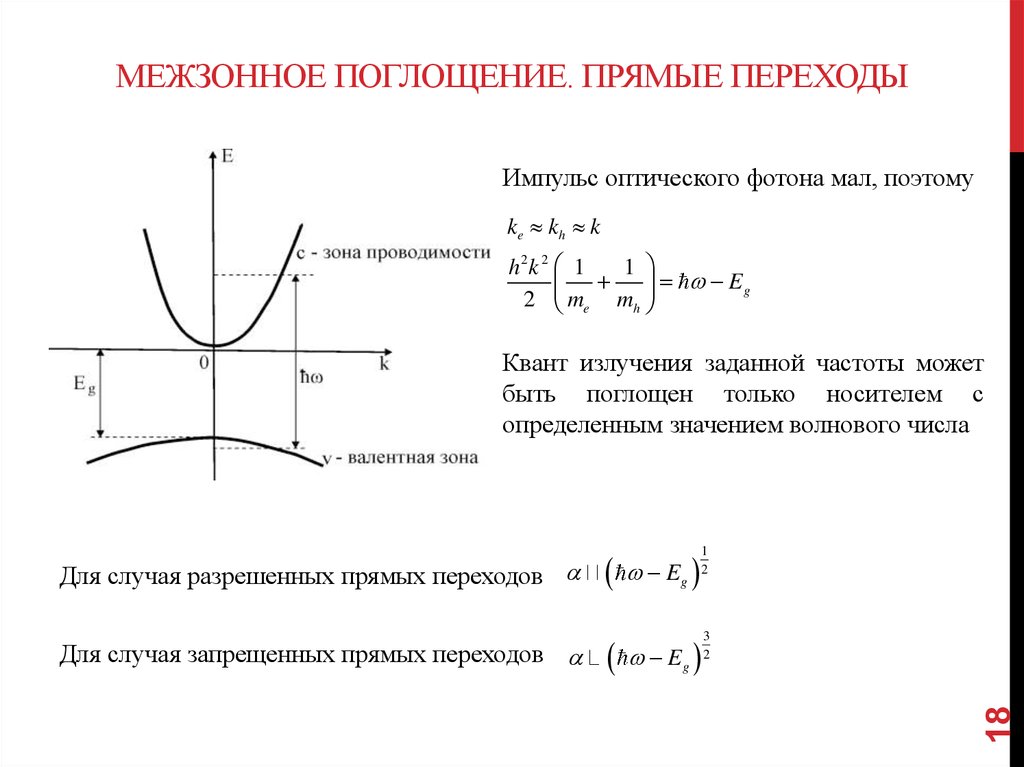
МЕЖЗОННОЕ ПОГЛОЩЕНИЕ. ПРЯМЫЕ ПЕРЕХОДЫИмпульс оптического фотона мал, поэтому
ke k h k
h2k 2 1
1
Eg
2 me mh
Квант излучения заданной частоты может
быть поглощен только носителем с
определенным значением волнового числа
Для случая запрещенных прямых переходов
Eg
Eg
3
2
18
Для случая разрешенных прямых переходов
1
2
19. Межзонное поглощение. Непрямые переходы
МЕЖЗОННОЕ ПОГЛОЩЕНИЕ. НЕПРЯМЫЕ ПЕРЕХОДЫЭнергия
C
Непрямые переходы возможны при участии
третьей частицы (фонона), обеспечивающей
выполнение закона сохранения импульса.
c/
.f
u
.u
/
.
.i hn
/
Ec
/
Возможны процессы как с испусканием,
Ec
/
hn = Eg hn так и с поглощением фонона.
0
Волновой вектор k
Eu
B Eg
2
B T , T TD
Непрямые переходы характерны для кремния при 1.1 3.4 эВ
19
(Nd:YAG-лазер, волоконный иттербиевыый лазер)
20. Поглощение на свободных носителях
ПОГЛОЩЕНИЕ НА СВОБОДНЫХ НОСИТЕЛЯХПоглощение излучения свободными носителями в полупроводниках аналогично
поглощению в металлах.
1
kp
2
2
b
b
r b r
2
r n02 , n02 – показатель преломления полупроводника в условиях отсутствия
свободных носителей
e ne
При p
e 2
- сечение поглощения
e
2
0cn0 m свободными носителями
При p
e ne
p
c
p
c
Характер зависимости α(ne) меняется при
ne n
m n02 0 2 2
e2
, p , Re 0
20
Зависимость коэффициента поглощения от
концентрации свободных носителей
21. ВЛИЯНИЕ СВОБОДНЫХ Носителей на оптические свойства полупроводника
ВЛИЯНИЕ СВОБОДНЫХ НОСИТЕЛЕЙ НА ОПТИЧЕСКИЕСВОЙСТВА ПОЛУПРОВОДНИКА
При каких концентрациях свободных носителей они начинают существенно влиять
на оптические свойства полупроводника?
Сравним коэффициенты межзонного поглощения и коэффициент поглощения
на свободных носителях для кремния на длине волны 1.06 мкм.
VC 103 м 1
e 10 22 м 2
Соответственно влиянием свободных электронов на коэффициент
поглощения можно пренебречь при ne
VC
e
1019 см3 .
Зависимость коэффициента отражения кремния
от концентрации свободных носителей
ne n 5 1021 см 3
При
коэффициент
отражения практически не меняется.
21
Такие уровни фотовозбуждения достижимы
только при воздействии ультракоротких
лазерных импульсов.
22. Фотовозбуждение полупроводников лазерным излучением
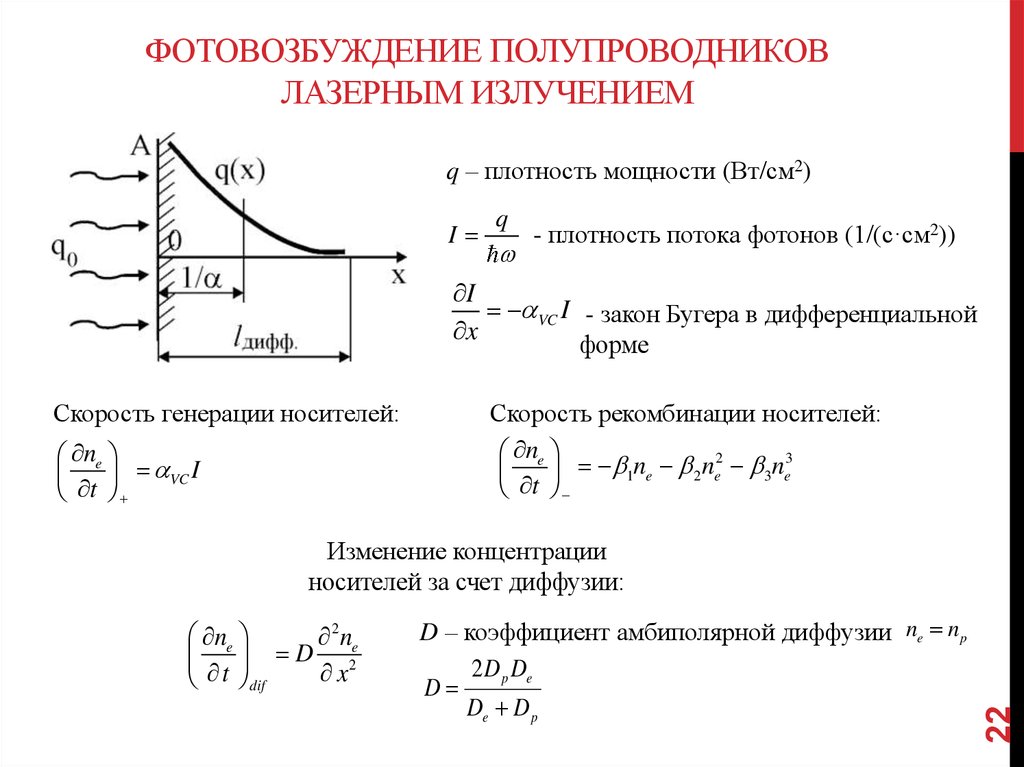
ФОТОВОЗБУЖДЕНИЕ ПОЛУПРОВОДНИКОВЛАЗЕРНЫМ ИЗЛУЧЕНИЕМ
q – плотность мощности (Вт/см2)
I
q
- плотность потока фотонов (1/(с·см2))
I
VC I - закон Бугера в дифференциальной
x
форме
Скорость генерации носителей:
ne
VC I
t
Скорость рекомбинации носителей:
ne
2
3
1ne 2 ne 3ne
t
ne
2 ne
D 2
t
x
dif
D – коэффициент амбиполярной диффузии ne n p
2 D p De
D
De D p
22
Изменение концентрации
носителей за счет диффузии:
23. Фотовозбуждение полупроводников лазерным излучением
ФОТОВОЗБУЖДЕНИЕ ПОЛУПРОВОДНИКОВ ЛАЗЕРНЫМИЗЛУЧЕНИЕМ
Уравнение описывающее кинетику фотовозбуждения полупроводника имеет вид:
ne
2 ne
D 2 VC I 1ne 2 ne2 3ne3
t
x
ne
0 - отсутствие потока электронов на
x x 0
границе
ne t 0 0
I
I I x 0 1 R I 0
Уравнение для плотности потока фотонов:
x
Начальные и граничные условия:
При VC const (ne ) имеем I 1 R I 0 exp VC x
Решение уравнения для концентрации устроено таким образом, спустя некоторое
время tst устанавливается стационарное распределение концентрации N(x).
tst
N
2 N
D 2 VC I 1 N 2 N 2 3 N 3
x
23
VC I
Стационарное
распределение
концентрации
может быть определено из уравнения:
24. Фотовозбуждение полупроводников лазерным излучением
ФОТОВОЗБУЖДЕНИЕ ПОЛУПРОВОДНИКОВ ЛАЗЕРНЫМИЗЛУЧЕНИЕМ
1. Основной вклад вносят диффузия и линейная рекомбинация.
N
x 0
VC 1 I
x 0
1 VC D 1
1 1 1
l
1
VC
D 1
- размер фотовозбужденной области
2. Основной вклад вносит Оже-рекомбинация (малые длительности импульса).
d 2N
D 2 VC Ie VC x 3 N 3
dx
Рассмотрим модельный случай когда источник можно перенести на границу, т.е.
d 2N
dN
D 2 3 N 3 D
dx
dx
1 R I 0
x 0
У такой задачи есть аналитическое решение:
2D
3
1
x
На поверхности:
D 2D
(1 R) I 0 3
(профиль концентрации гиперболический)
24
N ( x)
(1 R) I 0 2
N0
D
3
25. Насыщение межзонного поглощения
НАСЫЩЕНИЕ МЕЖЗОННОГО ПОГЛОЩЕНИЯВ тех случаях когда энергия кванта незначительно превышает ширину
запрещенной зоны при в процессе фотовозбуждения имеет место заполнение
электронных уровней у дна зоны проводимости и синхронно идущее обеднение
электронами потолка валентной зоны. При достижении определенной
концентрации процесс поглощения прекращается.
Коэффициент межзонного поглощения можно приближенно принять равным:
VC (ne ) VC (0) 1
ne
nmax
nmax – концентрация, при которой межзонные
переходы полностью прекращаются
Без учета диффузии и рекомбинации имеем:
Решение этой системы имеет вид “волны просветления”,
движущейся со скоростью v.
v
(1 R) I 0
nmax
19
3
При nmax 10 см
2 1
(1 R) I 0 10 см с
23
v 104 см / c
25
ne
VC (ne ) I
t
I
VC (ne ) I
x
26.
26В отличие от металлов набор эффектов сопровождающих лазерное воздействие в
полупроводниках
гораздо
шире.
Поглощение
лазерного
излучения
сопровождается
генерацией переносом и рекомбинацией неравновесных
носителей. Рост концентрации свободных электронов приводит к увеличению
коэффициента объемного поглощения, а при приближении их плазменной
частоты к частоте лазерного излучения к сильному росту, а затем к резкому
уменьшению величины поглощательной способности. При некоторых условиях
возможно уменьшение коэффициента межзонного поглощения из-за эффекта
насыщения. В то же время с ростом температуры может быстро увеличиваться
коэффициент межзонного поглощения.
27. Спасибо за внимание
27СПАСИБО ЗА ВНИМАНИЕ























 Физика
Физика








