Площадь прямоугольника

1.

2. Площадь прямоугольника

S=ab
а
b
Задача: найти площадь прямоугольника, если
диагональ равна 10 см, а одна из сторон
6см.
25.02.2019
2

3. Решение

a
d
По теореме Пифагора
b
d²=a²+b² => b²=d²-a², b²=10²-6²=100-36=64
b=√64=8см
S=6·8=48см²
Ответ : 48 см²
25.02.2019
3

4. Площадь параллелограмма

h
S=a·h
a
a
α
b
25.02.2019
S=a·b·sinα
4

5. Задача: стороны параллелограмма равны 4,2см и 5,6см. Высота, проведенная к большей стороне, равна 3,3см. Вычислите вторую

высоту этого
параллелограмма.
5,6см
h
4,2см
3,3см
Решение
S=3,3∙5,6=4,2∙h
h=
h=4,4 см
Ответ: 4,4 см
25.02.2019
5

6. Задача: в параллелограмме внутренние односторонние углы при диагонали равны 30º и 45º, а одна из сторон равна 4см.Найдите

площадь
параллелограмма.
Решение:
45º
30º
x
По теореме синусов:
4см
x=
x=√2см
S=4•√2•sin 75°=
25.02.2019
6

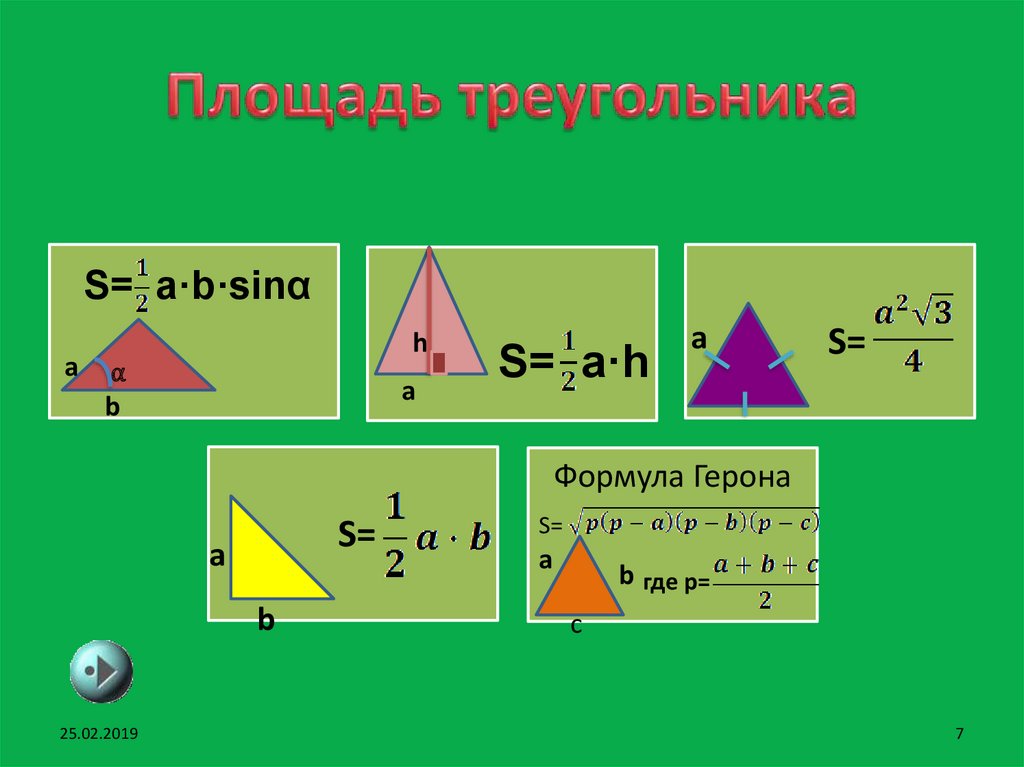
7. Площадь треугольника

S= a·b·sinα
a
h
α
a
b
S= a·h
a
S=
Формула Герона
S=
a
b
25.02.2019
S=
a
b где р=
c
7

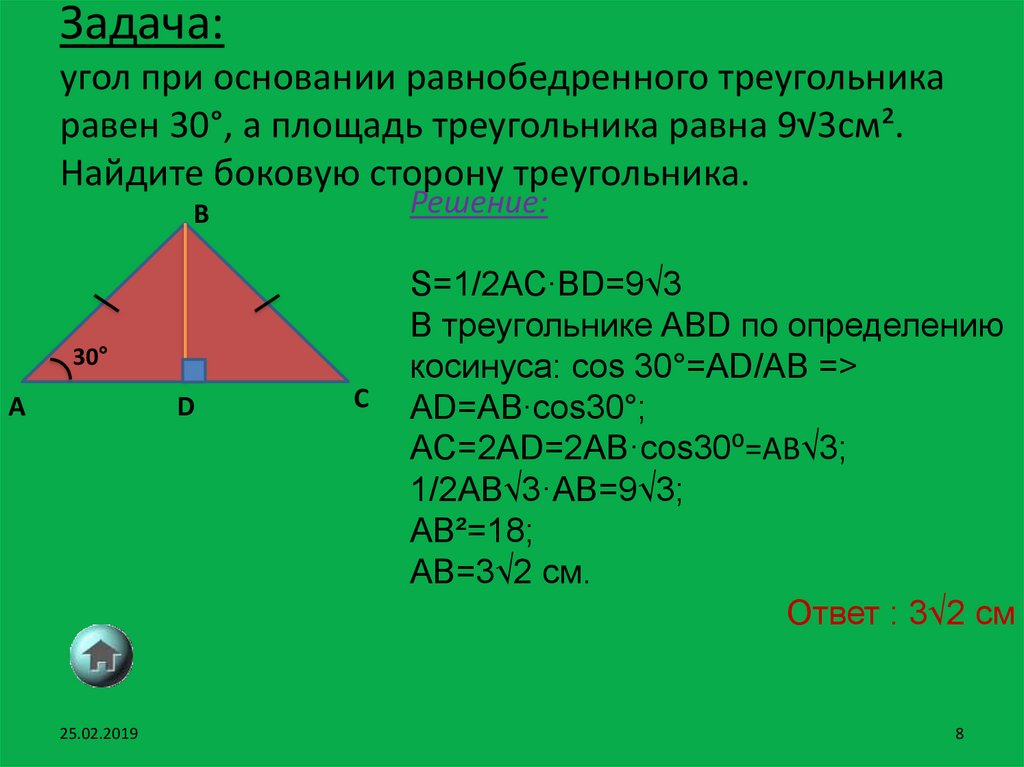
8. Задача: угол при основании равнобедренного треугольника равен 30°, а площадь треугольника равна 9√3см². Найдите боковую сторону

треугольника.
Решение:
B
30°
A
D
25.02.2019
C
S=1/2AC∙BD=9√3
В треугольнике ABD по определению
косинуса: cos 30°=AD/AB =>
AD=AB∙cos30°;
AC=2AD=2AB·cos30⁰=AB√3;
1/2AB√3·AB=9√3;
AB²=18;
AB=3√2 см.
Ответ : 3√2 см
8

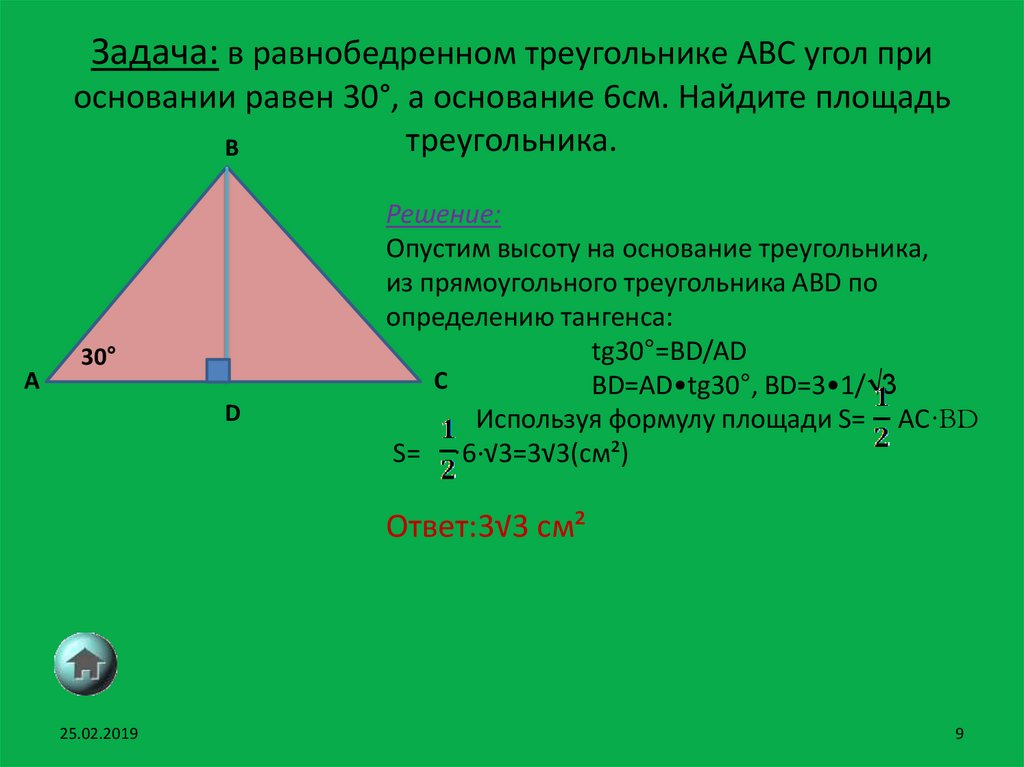
9. Задача: в равнобедренном треугольнике ABC угол при основании равен 30°, а основание 6см. Найдите площадь треугольника.

B
A
30°
D
Решение:
Опустим высоту на основание треугольника,
из прямоугольного треугольника ABD по
определению тангенса:
tg30°=BD/AD
C
BD=AD•tg30°, BD=3•1/√3
Используя формулу площади S= AC·BD
S= ·6∙√3=3√3(см²)
Ответ:3√3 см²
25.02.2019
9

10. Задача: высота правильного треугольника равна 4см. Найдите площадь этого треугольника.

h
a
Решение:
S=
a²=h²+
,по теореме Пифагора
, a²-
=h²,
= h²,
a²=2h², a²=2·4²,a=4√2, S=8√3(см²)
Ответ :8√3см²
25.02.2019
10

11. Задача: площадь прямоугольного равнобедренного треугольника равна 16см². Найдите гипотенузу этого треугольника.

Решение :
c
a
a
S=1/2a∙a=1/2a²=16
a²=16∙2=32 см²
a=√32=4√2 см
По теореме Пифагора: c²=a²+a²=2a²
c²=2∙32=64
c=√64=8 см
Ответ: 8 см
25.02.2019
11

12. Задача: стороны треугольника равны 8см, 6см,4см. Найдите меньшую высоту треугольника.

6
C
8
D
Решение:
A
меньшая высота проводится к большей
4 стороне ,
B т.е. AD. Используя формулу Герона найдём
площадь треугольника:
S=
; где p=
p=9см, S=3√15(см²);
Используя формулу площади треугольника
S=1/2AD∙CB найдём высоту AD.
1/2AD∙CB=3√15; AD=(2∙3√15):8=
(см)
Ответ:
25.02.2019
см
12

13. Площадь трапеции

b
S=
Задача:
h
a
высота трапеции равна меньшему основанию и в два
раза меньше большего основания. Найдите высоту
трапеции, если её площадь равна 54 см².
25.02.2019
13

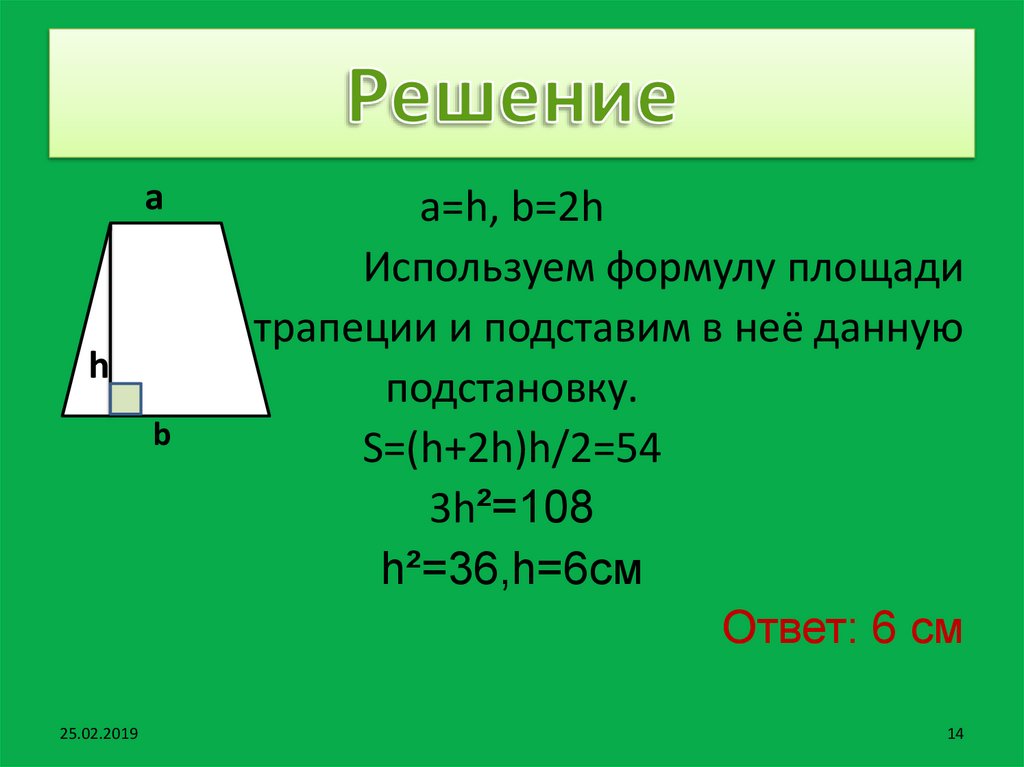
14. Решение

a
h
b
25.02.2019
a=h, b=2h
Используем формулу площади
трапеции и подставим в неё данную
подстановку.
S=(h+2h)h/2=54
3h²=108
h²=36,h=6см
Ответ: 6 см
14

15. Домашнее задание

• Страница 227, №26, №33.
• Выучить формулы.
25.02.2019
15

16. Спасибо за работу!

Желаю успехов в дальнейшей учёбе!
25.02.2019
16