Похожие презентации:
Решение задач по готовым чертежам по теме: "Некоторые свойства прямоугольных треугольников"
1.
Пятое декабряКлассная работа
2.
Некоторые свойствапрямоугольных треугольников
Свойство 10.
равна 900.
Сумма острых углов прямоугольного треугольника
Свойство 20. Катет прямоугольного треугольника, лежащий против
угла в 300, равен половине гипотенузы.
Свойство 30.
Если катет прямоугольного треугольника равен
половине гипотенузы, то угол, лежащий против этого катета, равен
300.
Свойство 40. В прямоугольном треугольнике медиана, проведенная
из вершины прямого угла, равна половине гипотенузы.
Свойство 50. Если медиана треугольника равна половине стороны,
к которой она проведена, то этот треугольник прямоугольный.
3.
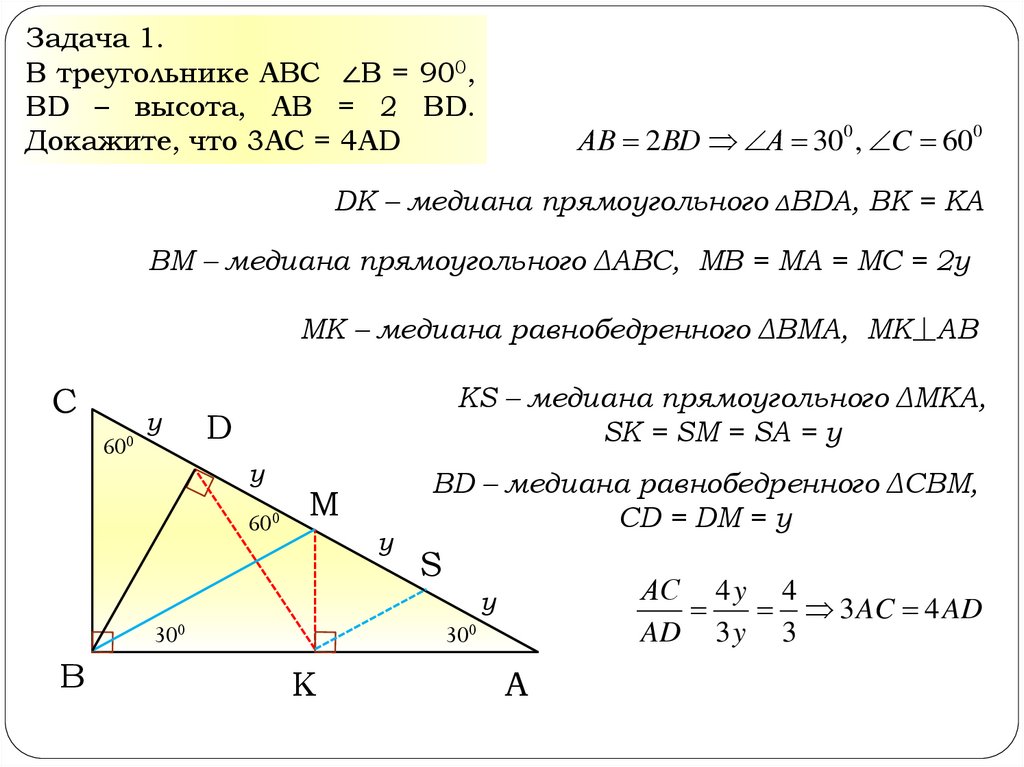
Задача 1.В треугольнике АВС ∠В = 900,
ВD – высота, АВ = 2 ВD.
Докажите, что 3АС = 4АD
АВ 2 ВD А 300 , C 600
DK – медиана прямоугольного ΔВDА, ВК = КА
ВМ – медиана прямоугольного ΔАВС, МВ = МА = МС = 2у
МК – медиана равнобедренного ΔВМА, МК⏊АВ
С
600
y
KS – медиана прямоугольного ΔМКА,
SK = SM = SA = у
D
y
600
M
y
BD – медиана равнобедренного ΔСВМ,
СD = DM = у
S
АС 4 y 4
3 AC 4 AD
AD 3 y 3
y
300
В
300
К
A
4.
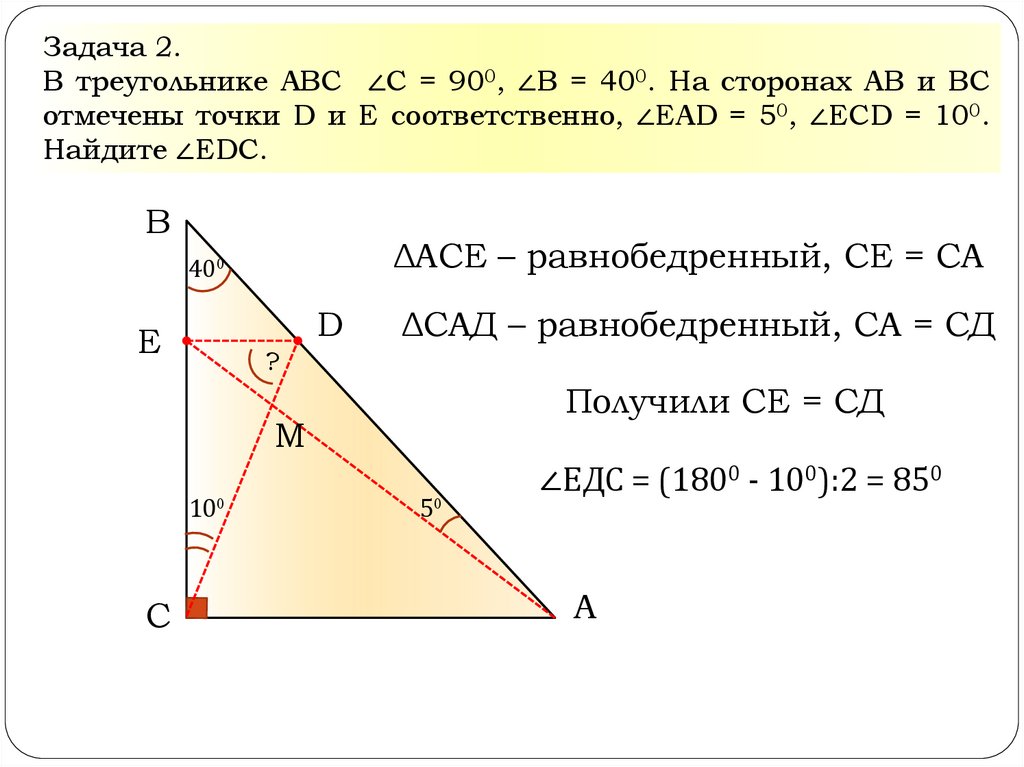
Задача 2.В треугольнике АВС ∠С = 900, ∠В = 400. На сторонах АВ и ВС
отмечены точки D и Е соответственно, ∠ЕАD = 50, ∠ЕСD = 100.
Найдите ∠ЕDС.
В
ΔАСЕ – равнобедренный, СЕ = СА
400
D
Е
ΔСАД – равнобедренный, СА = СД
?
Получили СЕ = СД
M
100
С
50
∠ЕДС = (1800 - 100):2 = 850
A
5.
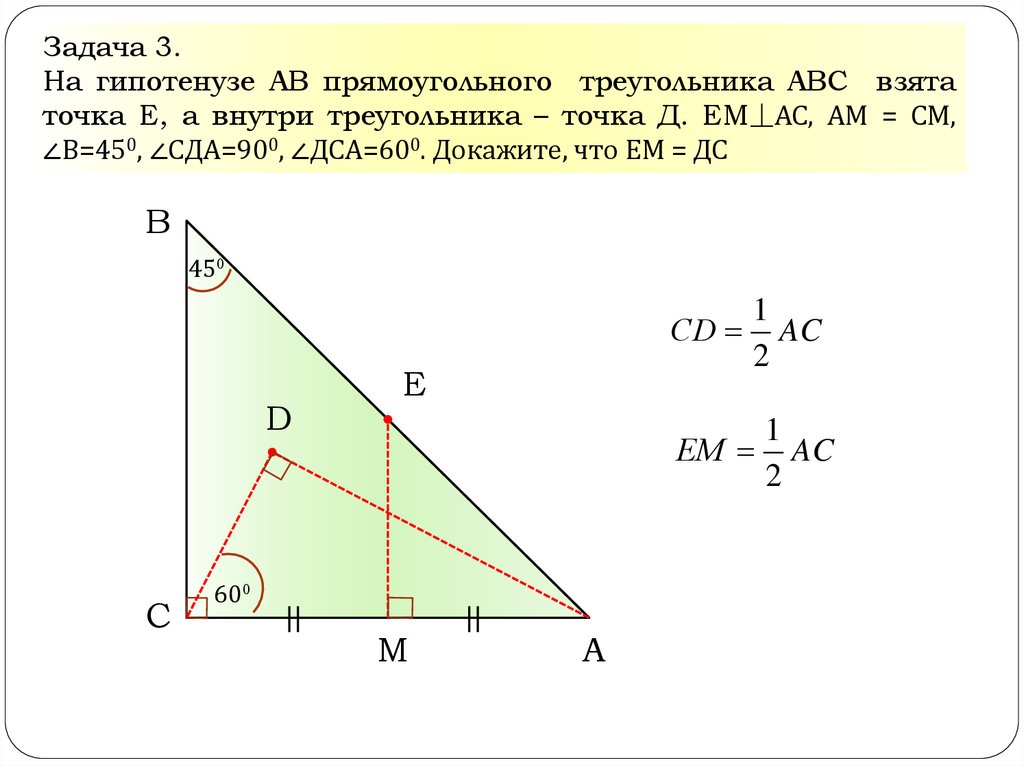
Задача 3.На гипотенузе АВ прямоугольного треугольника АВС взята
точка Е, а внутри треугольника – точка Д. ЕМ⏊АС, АМ = СМ,
∠В=450, ∠СДА=900, ∠ДСА=600. Докажите, что ЕМ = ДС
В
450
D
С
1
СD AC
2
Е
1
ЕМ AC
2
600
M
A
6.
Задача 4. Один из углов прямоугольного треугольника равен 60°, асумма гипотенузы и меньшего катета равна 18 см. Найдите
гипотенузу и меньший катет.
7.
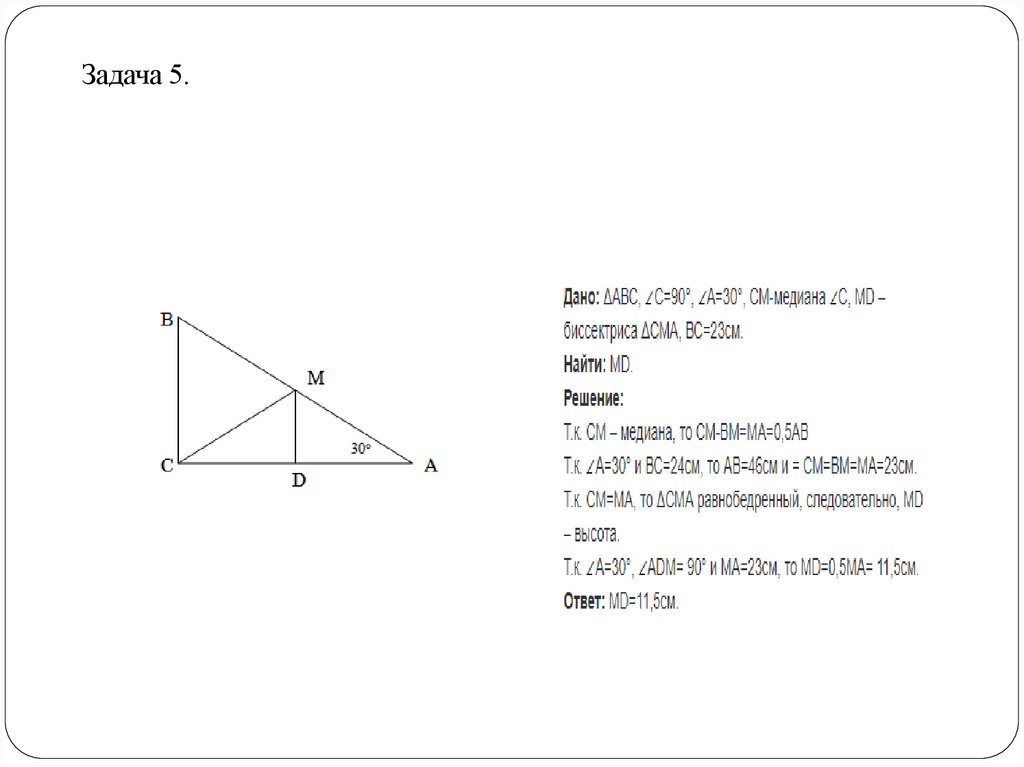
Задача 5.8.
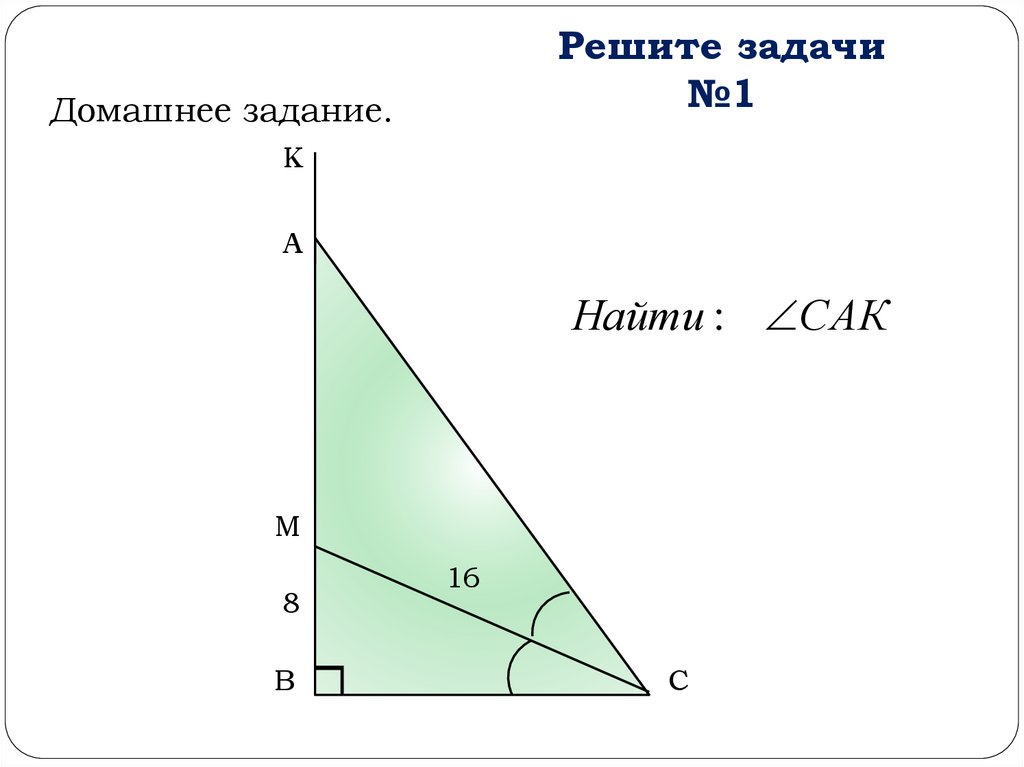
Решите задачи№1
Домашнее задание.
К
А
Найти : САК
М
8
В
16
С
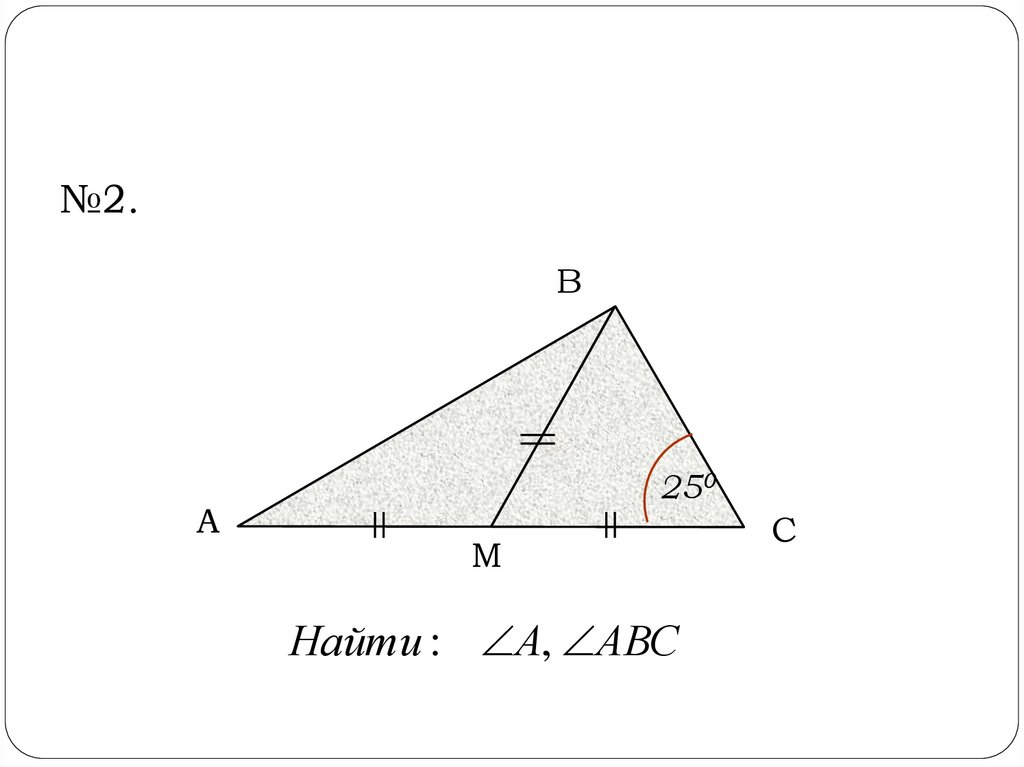
9.
№2.В
А
250
М
Найти : А, АВС
С
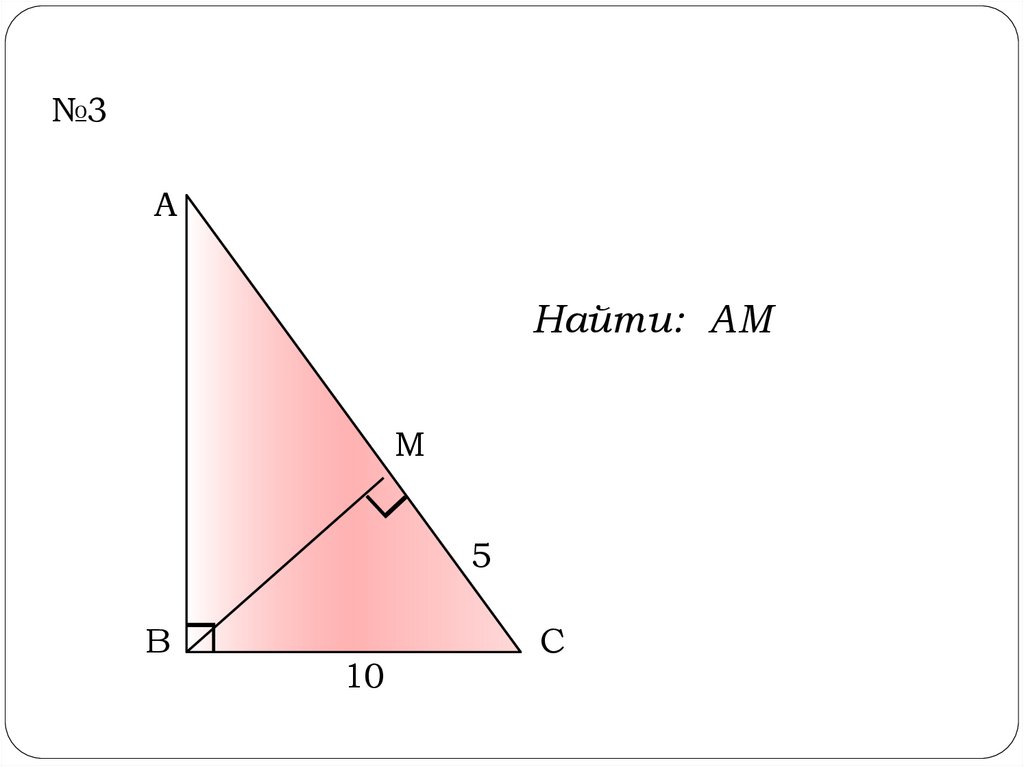
10.
№3А
Найти: АМ
М
5
В
10
С



 Математика
Математика








