Подобие треугольников. Математическая игра

1.

2.

• 1 гонка
• 2 гонка
• 3 гонка
• 4 гонка
• УРА!!!

3.

Первая команда
Как
продолжить
утверждение,
чтобы оно
стало
верным ?
«Два треугольника
называются
подобными, если…»
1
Вторая команда
Продолжите
фразу так, чтобы
утверждение
стало верным.
«Если два угла одного
треугольника…»

4.

Первая команда
Как
продолжить
утверждение,
чтобы оно
стало
верным ?
«Если три стороны
одного
треугольника…»
2
Вторая команда
Продолжите
фразу так, чтобы
утверждение
стало верным.
«Отношение площадей
подобных
треугольников…»

5.

Первая команда
Как
продолжить
утверждение,
чтобы оно
стало
верным ?
«Средней линией
треугольника
называется…»
3
Вторая команда
Продолжите
фразу так, чтобы
утверждение
стало верным.
«Средняя линия
треугольника…»

6.

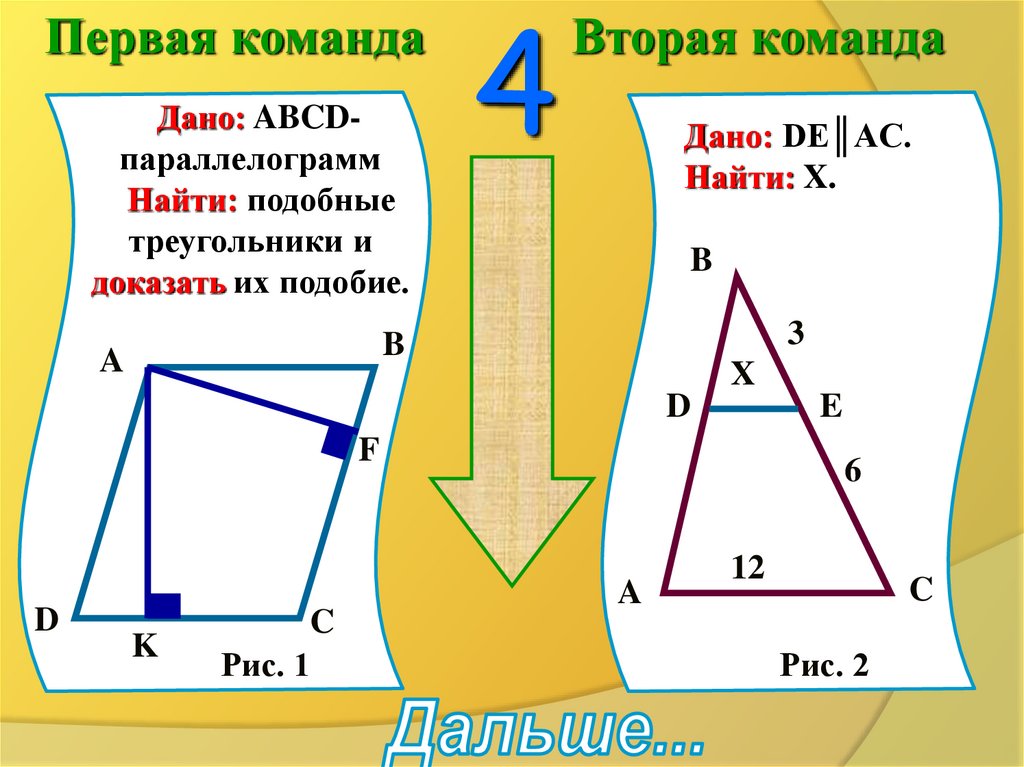
Первая команда
Дано: ABCDпараллелограмм
Найти: подобные
треугольники и
доказать их подобие.
4
Вторая команда
Дано: DE║AC.
Найти: X.
B
3
B
A
X
D
E
F
D
K
C
Рис. 1
6
A
12
C
Рис. 2

7.

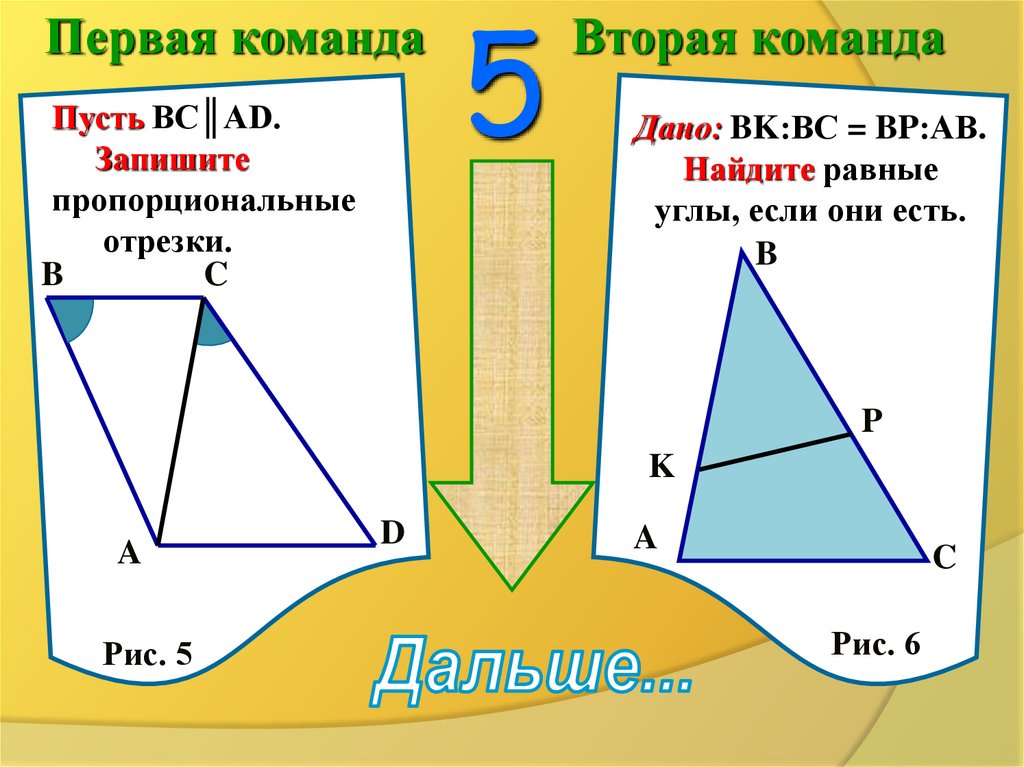
Первая команда
Пусть BC║AD.
Запишите
пропорциональные
отрезки.
B
C
5
Вторая команда
Дано: BK:ВС = BP:АВ.
Найдите равные
углы, если они есть.
B
P
K
A
Рис. 5
D
A
C
Рис. 6

8.

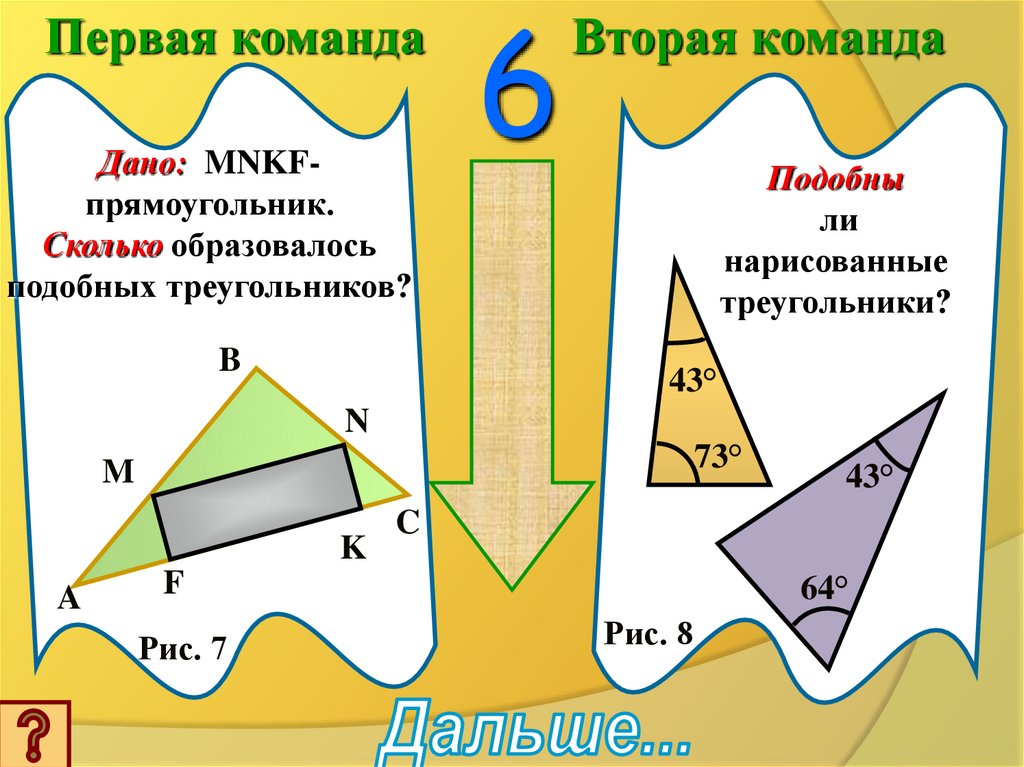
Первая команда
Дано: MNKFпрямоугольник.
Сколько образовалось
подобных треугольников?
B
6
Вторая команда
Подобны
ли
нарисованные
треугольники?
43°
N
73°
M
K
A
C
F
Рис. 7
43°
64°
Рис. 8

9.

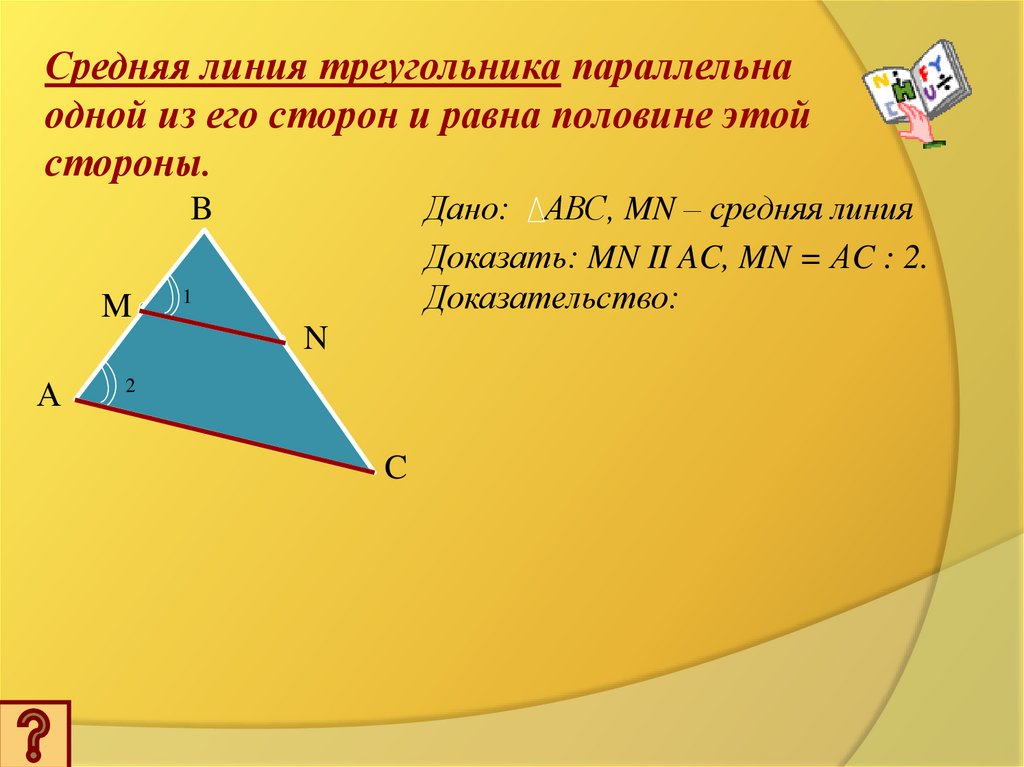
Средняя линия треугольника параллельна
одной из его сторон и равна половине этой
стороны.
Дано: АВС, MN – средняя линия
Доказать: MN II AC, MN = АC : 2.
Доказательство:
B
M
1
N
А
2
C

10.

Медианы треугольника пересекаются в одной
точке, которая делит каждую медиану в
отношении 2 : 1, считая от вершины.
Решение.
С
А1В1 II АВ
В1
4
А
2
1
О
А
1
3
С1
В
1 2, 3 4
АОВ
А1ОВ1
АО ВО
АВ
.
А1О В1О А1 В1
АО = 2А1О,
= 2В1О
Аналогично: СО = 2С1О.
АВ = 2А1В1
ВО

11.

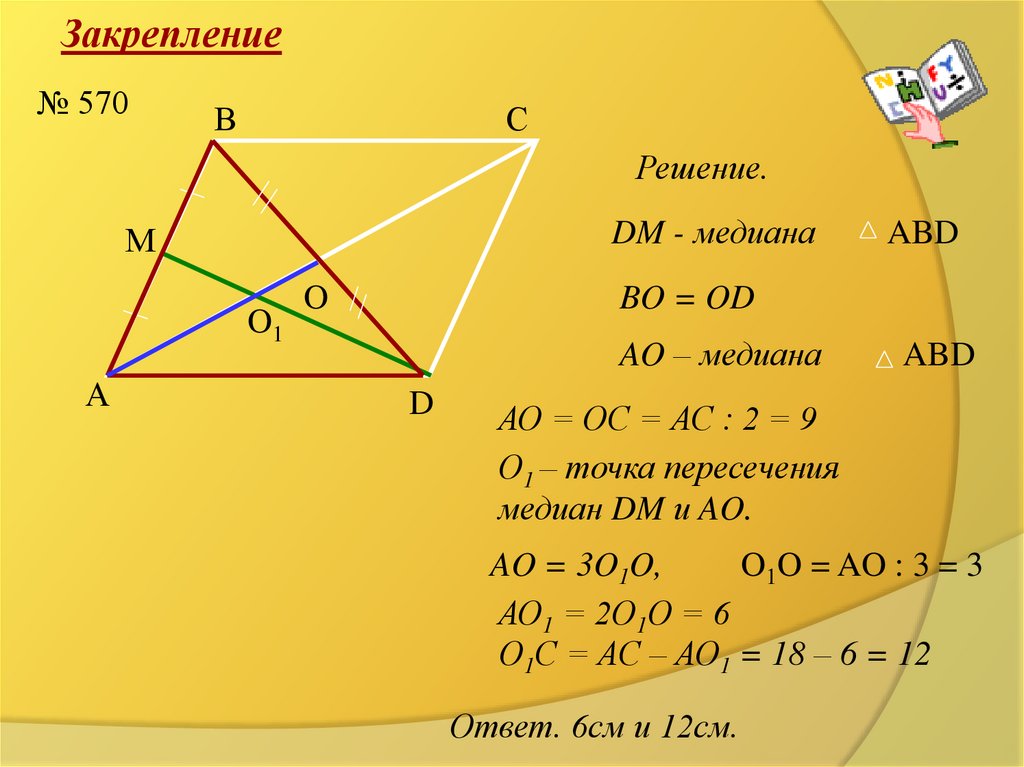
Закрепление
№ 570
В
С
Решение.
DM - медиана
М
O1
А
O
ABD
BO = OD
AO – медиана
D
ABD
АО = ОС = АС : 2 = 9
О1 – точка пересечения
медиан DM и AO.
AO = 3O1O,
O1O = AO : 3 = 3
АО1 = 2О1О = 6
О1С = АС – АО1 = 18 – 6 = 12
Ответ. 6см и 12см.

12.

Итог урока
1.
Отрезок, соединяющий середины двух сторон
треугольника, называется средней линией
треугольника.
2.
Средняя линия треугольника параллельна одной из
его сторон и равна половине этой стороны.
3.
Медианы треугольника пересекаются в одной точке,
которая делит каждую медиану в отношении 2 : 1,
считая от вершины.

13.

ДОМАШНЕЕ ЗАДАНИЕ
1. п. 62-63
2. №568
3. Практическое применение
подобия треугольников для измерения
отрезков на местности.

14.

гонки
I
команда
II
команда