Распространение волн в нелинейной среде

1.

Распространение волн в нелинейной среде
Предположим, что
E(r, t ), P(r, t )
можно разложить по плоским волнам:
Лекция 7-8
Нелинейная оптика
Общий вид волнового уравнения в нелинейной среде:
Амплитуды поля и компонент нелинейной поляризации – не зависят от времени
(проблема описания нестационарных нелинейных процессов вынесена за
скобки)

2.

Распространение волн в нелинейной среде
Вспомнив, что
Лекция 7-8
Нелинейная оптика
исходное волновое уравнение
запишется в виде системы уравнений
Замечания:
( NL )
1. В общем виде, нелинейная поляризация P
определяется всеми
полями En ( k n , n )
2. Это означает, что перед нами система связанных уравнений
3. Связанность уравнений означает перераспределение энергии между
различными компонентами поля
4. Частоты справа и слева 0динаковые, а волновые вектора могут быть
разными (закон сохранения энергии в стационарном случае и
возможность нарушения закона сохранения импульса)

3.

Связанные волны в нелинейной среде
Лекция 7-8
Нелинейная оптика
Система связанных уравнений для трехволнового процесса примет вид:

4.

Приближения, упрощающие жизнь:
1. приближение бесконечных плоских волн
2. приближение заданной интенсивности накачки
3. приближение заданного поля
4. приближение медленно меняющихся амплитуд
Лекция 7-8
Нелинейная оптика
Приближение медленно меняющихся амплитуд
Рассмотрим электромагнитную волну в нелинейной среде в виде
для простоты – распространяющуюся вдоль оси z
Амплитуда волны – функция, зависящая от координаты из-за нелинейного
взаимодействия
Предположим, что зависимость амплитуды от координаты слабая:

5.

Приближение медленно меняющихся амплитуд
Лекция 7-8
Нелинейная оптика
Разделив поле на продольную и поперечную компоненты,
волновое уравнение запишется в виде двух уравнений:
тогда, используя:
получим:

6.

Приближение медленно меняющихся амплитуд
Физический смысл приближения – пренебрежение обратной волной
нелинейного сигнала.
Лекция 7-8
Нелинейная оптика
Действительно, рассмотрим волновое уравнение в изотропной пластине
2 2
4 2 NL
2 2 E( , z ) 2 P ( , z )
c
c
z
Будем решать методом функций Грина. ФГ определяется как решение
уравнения
2
2
2 2 G ( z, z ') ( z, z ')
c
z
ФГ для однородной пластины принимает вид
1 ik ( z z ')
, z z'
i 2k e
G ( z, z ')
1 e ik ( z z ') , z z '
i 2k

7.

Приближение медленно меняющихся амплитуд
Решение волнового уравнения ищем в виде
z ' l
4 2 NL
G
E
E( , z ) 2 P ( z ')G( z, z ')dz ' G
E
z
'
z
'
c
z ' 0
0
Подставляя выражение для ФГ:
Лекция 7-8
Нелинейная оптика
l
l
2 2 z NL
ik ( z z ')
NL
ik ( z z ')
E( , z )
P ( z ')e
dz ' P ( z ')e
dz '
2
ikc 0
z
z ' l
G
E
G
E
z ' z ' 0
z '
Записав поле внутри пластины как суперпозицию двух разбегающихся волн
E( , z ) EF ( z )ei ( kz t ) EB ( z )ei ( kz t )
и граничные условия на гранях пластины в виде
EF z 0, EB z 0
(постоянство амплитуд вне нелинейной пластины)

8.

Приближение медленно меняющихся амплитуд
Лекция 7-8
Нелинейная оптика
получаем:
z ' l
G
E
i ( kz t )
i ( kz t )
G
E
E
(0)
e
E
(
l
)
e
F
B
z '
z ' z ' 0
Окончательно:
2 2 z NL
i ( kz ' t )
E F ( z ) E F (0) i
P
(
z
')
e
dz ',
2
kc 0
2 2 l NL
i ( kz ' t )
E B ( z ) E B (l ) i
P
(
z
')
e
dz '
2
kc z
Но это есть решения двух дифференциальных уравнений
EF
2 2 NL
i ( kz t )
i
P
(
,
z
)
e
,
2
z
kc
EB
2 2 NL
i ( kz t )
i
P
(
,
z
)
e
z
kc 2
что соответствует уравнениям ММА с
EB 0

9.

Генерация суммарной частоты в полубесконечной среде
В задаче о генерации суммарной частоты участвуют три связанные волны,
E( 1 ), E( 2 ), E( 3 )
каждая из которых раскладывается на две компоненты,
E( i ) E// ( i ) E ( i )
Лекция 7-8
Нелинейная оптика
удовлетворяющим волновому уравнению
где
P(2) ( 3 ) (2) ( 3 1 2 ) : E( 1 )E( 2 )

10.

Генерация суммарной частоты в полубесконечной среде
Лекция 7-8
Нелинейная оптика
В приближении:
-бесконечных плоских волн
- заданной интенсивности накачки
- полубесконечности среды с плоской границей
- кубичности (изотропности) среды
уравнения для E( 1 ), E( 2 ) линейны.
Записав волны накачки в виде
а квадратичную поляризацию в виде
P(2) ( 3 ) P3(2) exp[i (k 3sr 3t )]
третье связанное уравнение будет иметь решение в виде
(2)
2
4
P
4
3// ik 3 sr i 3t
ET ( 3 ) Aeik 3T r 2 2 3 2 P3(2)
e
e
// 3
c k3s k3T
и состоит из двух волн, связанной и свободной, с волновыми векторами
k 3s k1T k 2T , k 3T

11.

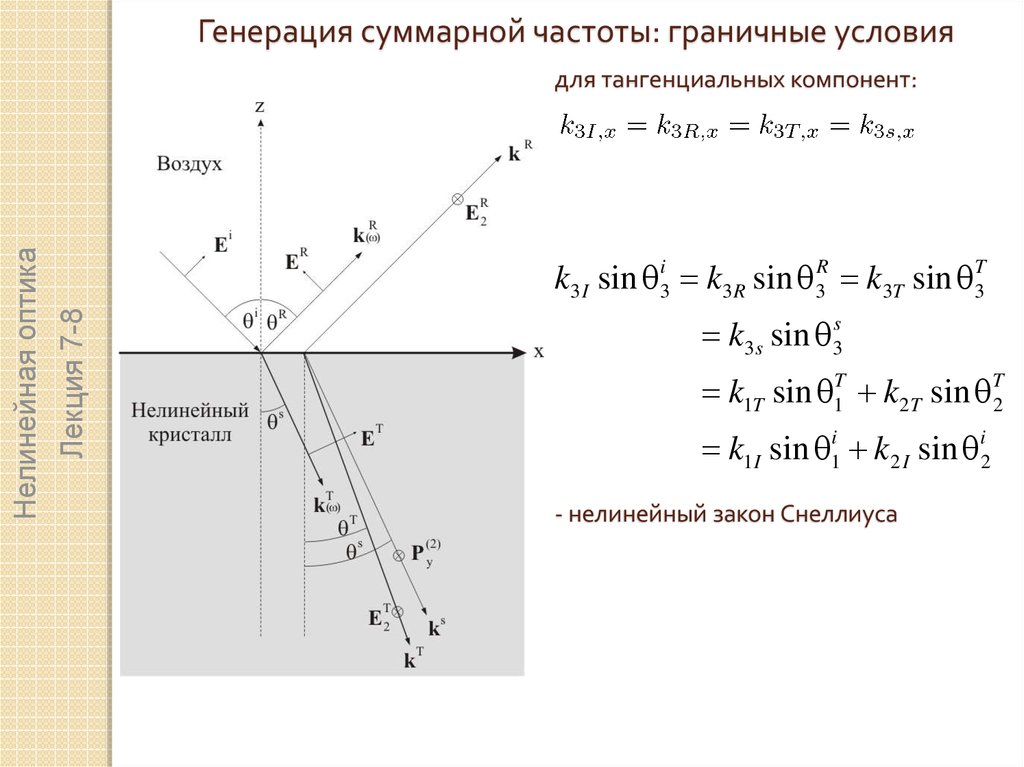
Генерация суммарной частоты: граничные условия
k3 I sin i3 k3 R sin 3R k3T sin T3
Лекция 7-8
Нелинейная оптика
для тангенциальных компонент:
k3s sin 3s
k1T sin 1T k2T sin T2
k1I sin 1i k2 I sin i2
- нелинейный закон Снеллиуса

12.

Генерация суммарной частоты: фазовый синхронизм
Запишем поле на суммарной частоте в виде
Лекция 7-8
Нелинейная оптика
тогда в рамках приближения ММА
где расстройка волновых векторов
Решение укороченных уравнений запишется в виде
далее полагаем
E3T (0) 0

13.

Генерация суммарной частоты: фазовый синхронизм
Интенсивность волны на суммарной частоте
2
c ( 3 )
I3 ( z)
E3T ( z )
2
Лекция 7-8
Нелинейная оптика
полная мощность волны определяется интегрированием по пучку:
при малой расстройке,
k3 k 1
, можно считать, что
E3T // E3T
и интенсивность волны на суммарной частоте запишется в виде

14.

Генерация суммарной частоты: фазовый синхронизм
I 3 ( k z z )
достигает максимума при
k 0
Лекция 7-8
Нелинейная оптика
то есть при выполнении условия фазового синхронизма
полуширина между первыми нулями (ширина синхронизма)
k HW z
типичная оценка: при
k HW
k3T
k3T z 2
l 1 cm, k3T 105 cm 1
ширина синхронизма очень мала:
k HW / k3T 10 4
NB: рассмотрен только изотропный случай, оптическую анизотропию
нужно рассматривать отдельно

15.

Условие фазового синхронизма
Итак, генерация суммарной частоты идет эффективно при выполнении
условия
kz 1
k определяет когерентную длину lcor 1 / k
в коллинеарной геометрии взаимодействия эффективная генерация
наблюдается при условии синхронизма
Лекции 7-8
Нелинейная оптика
волновая расстройка
Это условие можно переписать через показатели преломления
Это возможно при:
- аномальной дисперсии
- в двулучепреломляющих отрицательных одноосных кристаллах при
ne ( i ) n0 ( i )
Возможны два типа синхронизма:
«тип 1» - ooe
ne (2 ) no ( )
«тип 2» - oee
1
ne (2 ) no ( ) ne ( )
2
NB: рассмотрен только
прозрачный случай,
при наличии поглощения
нужно рассматривать более
строго