Связанные уравнения для трехволновых процессов при высокой эффективности преобразования

1.

При
-точном синхронизме,
-коллинеарном взаимодействии,
-малости потерь и
-выполнении приближения ММА,
связанные уравнения запишутся в виде:
Лекции 9-10
Нелинейная оптика
Связанные уравнения для трехволновых процессов
при высокой эффективности преобразования
где
в полосе прозрачности
K1 K2 K3 K
i 0 -угол между
ET ( i ) и ET , ( i )

2.

Соотношения Мэнли-Роу для трехволновых процессов
В среде без потерь перестановочные соотношения дадут
K1 K 2 K3 K
Лекции 9-10
Нелинейная оптика
Из связанных уравнений можно показать, что поток мощности
постоянен вдоль взаимодействующих волн (закон сохранения энергии) соотношения Мэнли-Роу.
Одновременно, выражение для баланса числа фотонов при трехволновых
взаимодействиях в плоскости z :
(число фотонов, родившихся на частоте 3 , равно числу фотонов,
аннигилировавших на частотах 1 , 2 )

3.

Связанные уравнения для трехволновых процессов
при высокой эффективности преобразования
Лекции 9-10
Нелинейная оптика
Введем новые комплексные переменные:
а также новую безразмерную переменную вместо координаты:
Система связанных уравнений запишется в виде:
du3
u1u2 sin ,
d
d
d
K ctg
ln u1u2 u3
d
d

4.

Связанные уравнения для трехволновых процессов
при высокой эффективности преобразования
Последнее из уравнений
можно проинтегрировать:
Лекции 9-10
Нелинейная оптика
Подставляя в систему последних уравнений выражений для
При граничном условии
E3T (0) 0 (u3 (0) 0)
, получим, что
0, / 2
тогда последнее уравнение редуцируется до вида
где введены обозначения
m1 u22 (0) u32 (0),
sin
m2 u32 (0) u12 (0)
NB: точное решение – здесь: Physical Review 127, 1918 (1962)

5.

Связанные уравнения для трехволновых процессов
при высокой эффективности преобразования
Лекции 9-10
Нелинейная оптика
Решение этого уравнения имеет вид эллиптического интеграла Якоби
где
,
а эллиптическая функция sn
координате с периодом
2
u1(0) , периодична по приведенной

6.

Генерация суммарной частоты
Лекции 9-10
Нелинейная оптика
Окончательное выражение для интенсивности трех волн примет вид:
Частным случаем генерации суммарной частоты является вариант
u1 (0) u2 (0), u3 (0) 0, 1
тогда

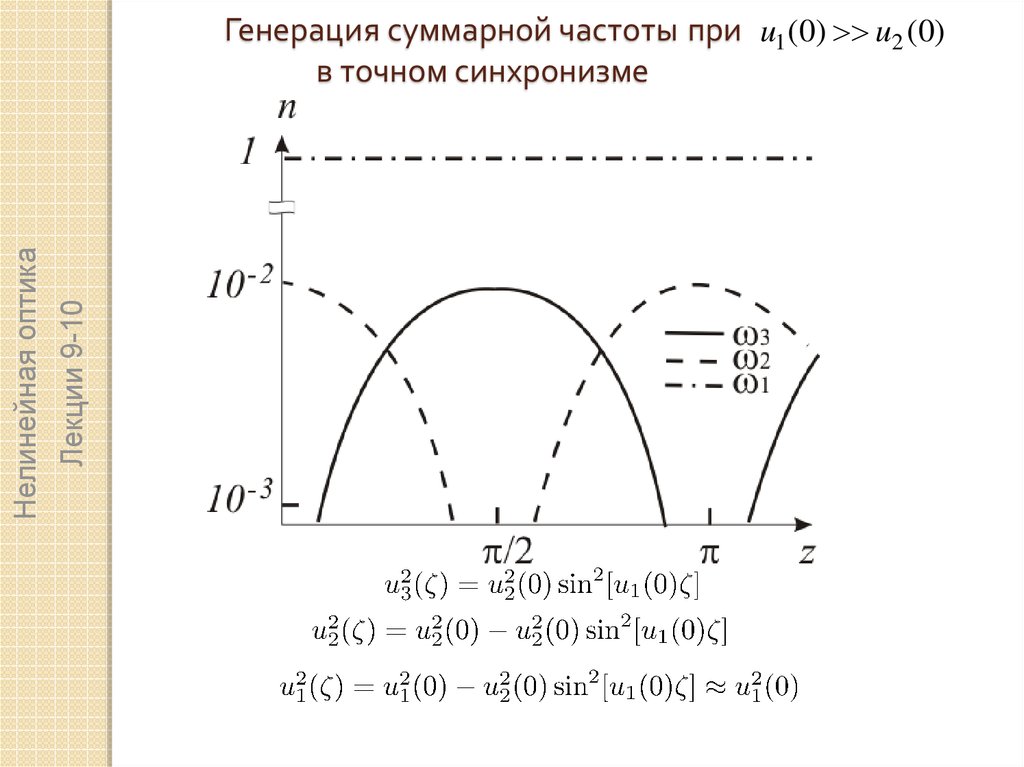
7.

Лекции 9-10
Нелинейная оптика
Генерация суммарной частоты при u1 (0) u2 (0)
в точном синхронизме

8.

Генерация суммарной частоты: накачки, равные
по мощности (генерация второй гармоники)
рассмотрим частный случай
Лекции 9-10
Нелинейная оптика
решение для интенсивности трех волн примет вид:
то есть:

9.

Четырехволновое смешение
Рассмотрим случай трех волн накачки
Лекции 9-10
Нелинейная оптика
-описывается кубичной нелинейностью
- отсутствует симметрийный запрет в центросимметричных средах
- существенно усиливается в окрестности резонансов
- часто используется с перестраиваемой бигармонической накачкой
(спектроскопия )
Em ( m ) Em exp(ik m r i mt )
m 1 , 2 , 3 , k m k1 , k 2,k 3
Результирующее поле на выходе
Es ( s ) Es exp(ik s r i s t )
является решением неоднородного волнового уравнения
2 s2
4 s2 (3)
2 ( s ) Es 2 P ( s )
c
c
с кубичной поляризацией
P(3) ( s ) (3) ( s 1 2
3 ) : E( 1 )E( 2 )E( 3 )

10.

Четырехволновое смешение: общий подход
Es,i ( z )
Лекции 9-10
Нелинейная оптика
В приближении ММА, распространении волны отклика вдоль оси z
и в приближении заданной накачки
2 s2
( k zˆ )k s c
(3)
i k z
E
E
E
1
e
e
2 ijkl 1, j 2,k 3,l
s ,i
где фазовая расстройка
k k1 k 2 k 3 k s izˆ( 1, j 2,k 3,l s,i )
m, j
При
- коэффициент затухания вдоль оси z
k 0
интенсивность отклика резонансно возрастает
z

11.

Четырехволновое смешение: коллинеарное усиление
Рассмотрим случай усиления одной из волн при мощных двух других:
s 1 2 3
Лекции 9-10
Нелинейная оптика
Es E3 , s 3 , k s k 3
k k1 1 k 2 ( 2 ),
тогда
При отсутствии истощения волн
E1, E2
Es ,i ( z ) Es ,i (0)exp gi ( z ) s ,i z ,
gi ( z )
Re gi ( z )
2 s2
( k zˆ )k s c
(3)
i k z
E
E
1
e
2 ijki 1, j 2,k
представляет собой коэффициент усиления

12.

Четырехволновое смешение: параметрическое усиление
с обратной волной
Рассмотрим случай четырехволнового усиления двух слабых волн,
распространяющихся в противоположных направлениях:
Es
- сигнальная волна,
E3 Ei
- холостая волна,
кристалле толщиной
Лекции 9-10
Нелинейная оптика
При выполнении условия фазового синхронизма в
l
1/2
g l
k
Es ( z 0) Es (l )cos 1 0 i s s
2 i ki
Ei ( z
где
при
1/2
i k s
l ) i
s ki
g l
Ei (0) tg 0 ,
2
g 0l
1 g 0 l
Es (l ) tg
Ei (0)cos
2
2
2 2
g0 s i KE E 2 ,
1 2
k s ki
2
2
2 (3)
K 2 ( s i 1 2 )
c
g0l осуществляется переход к режиму генерации