Средяя линия треугольника

1. Геометрия 8 класс Средняя линия треугольника

Автор: Бобель Юлия Анатольевна
учитель математики
ГОУ СОШ №313
Фрунзенский район
г. Санкт-Петербург

2. Оглавление

Средняя линия треугольника
Решение задач (урок 2)

3. Средняя линия треугольника

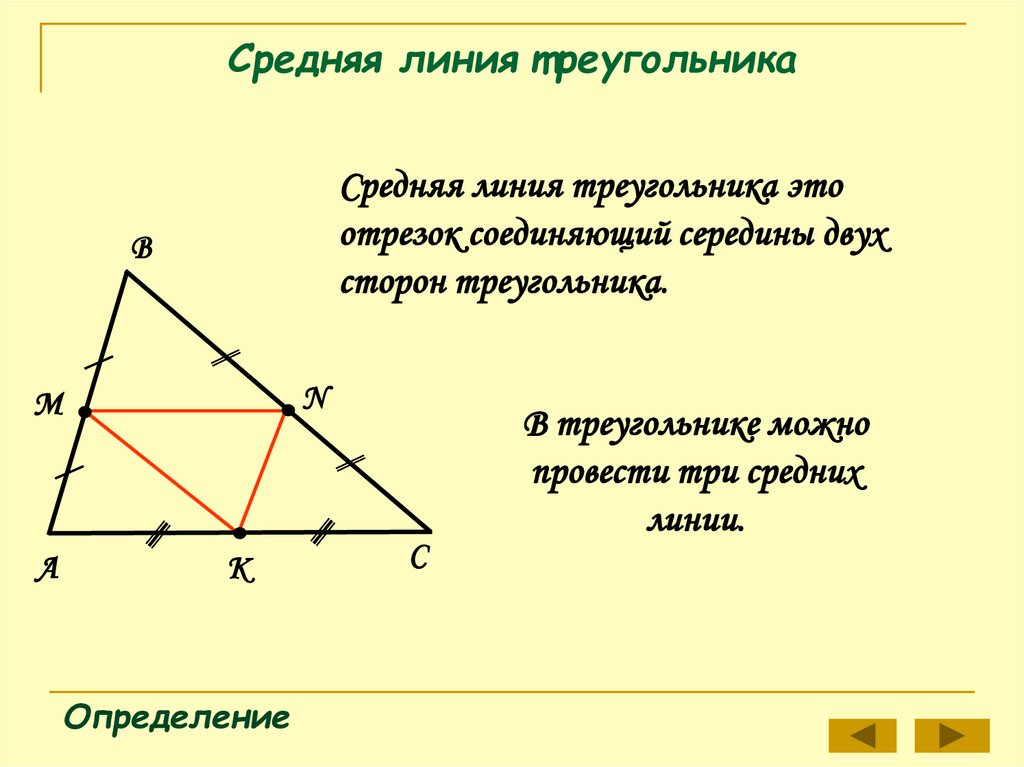
Средняя линия т реугольника
Средняя линия треугольника это
отрезок соединяющий середины двух
сторон треугольника.
В
N
М
А
К
Определение
С
В треугольнике можно
провести три средних
линии.

4. Средняя линия треугольника

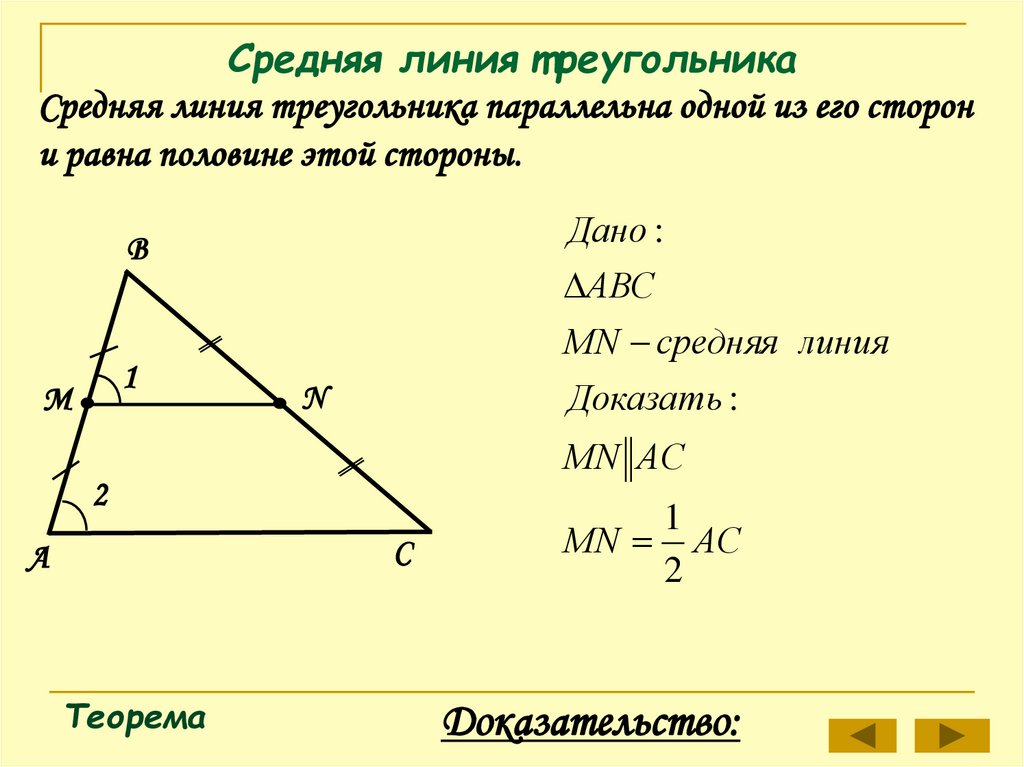
Средняя линия т реугольника
Средняя линия треугольника параллельна одной из его сторон
и равна половине этой стороны.
Дано :
В
1
М
АВС
МN средняя линия
Доказать :
N
МN АС
2
С
А
Теорема
1
МN АС
2
Доказательство:

5. Средняя линия треугольника

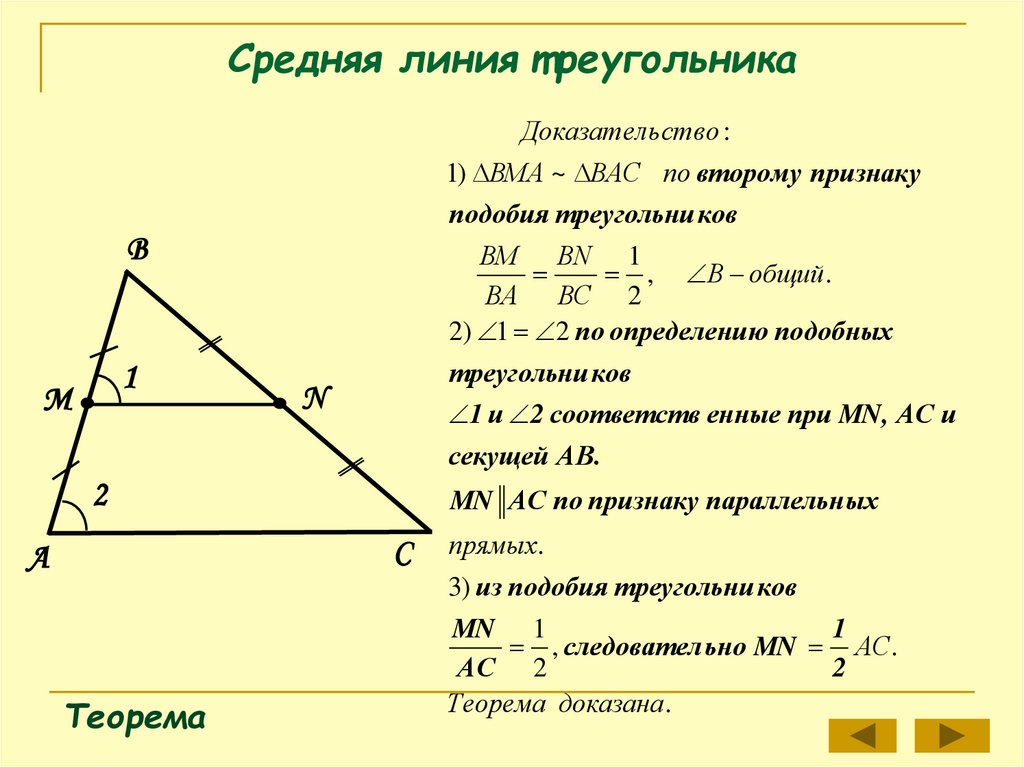
Средняя линия т реугольника
Доказатель ство :
1) ВМА ~ ВАС по второму признаку
подобия треугольни ков
М
В
ВМ ВN 1
, В общий.
ВА ВС 2
2) 1 2 по определени ю подобных
1
треугольни ков
1 и 2 соответств енные при MN, АС и
N
секущей АВ.
2
MN АС по признаку параллельн ых
С
А
прямых.
3) из подобия треугольни ков
Теорема
MN 1
1
, следовател ьно MN АС.
АС 2
2
Теорема доказана .

6. Средняя линия треугольника

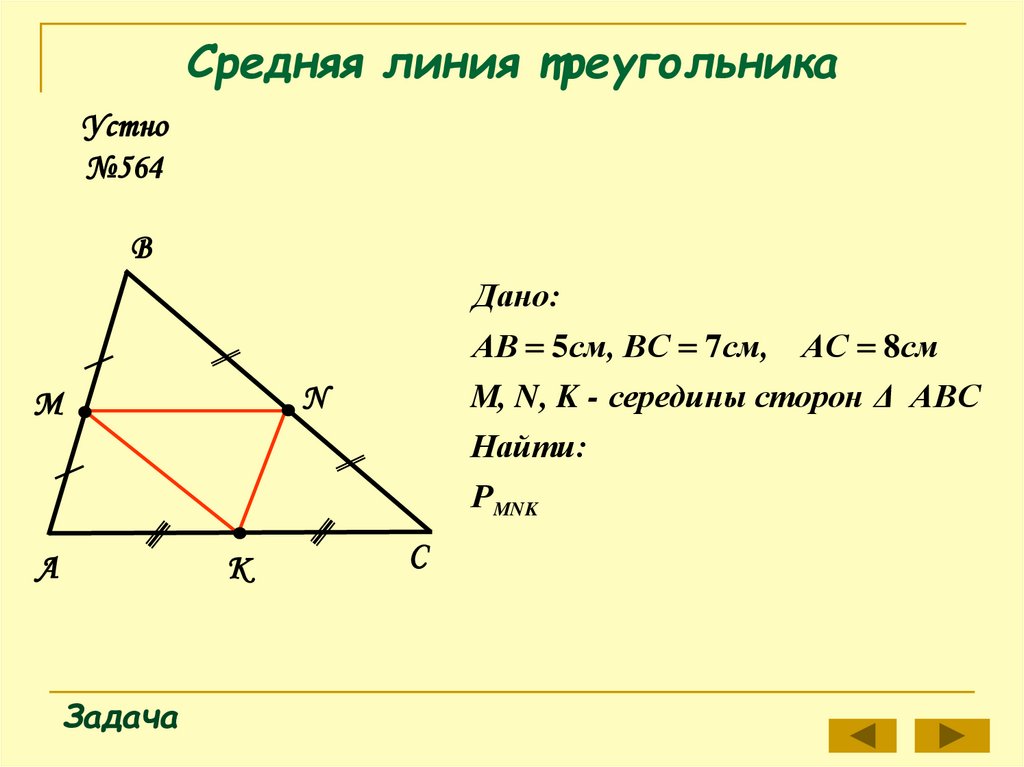
Устно
№564
В
Дано:
АВ 5см, ВС 7см,
M, N, K - середины сторон Δ АВС
N
М
Найти:
Р MNK
А
К
Задача
АС 8см
С

7. Средняя линия треугольника

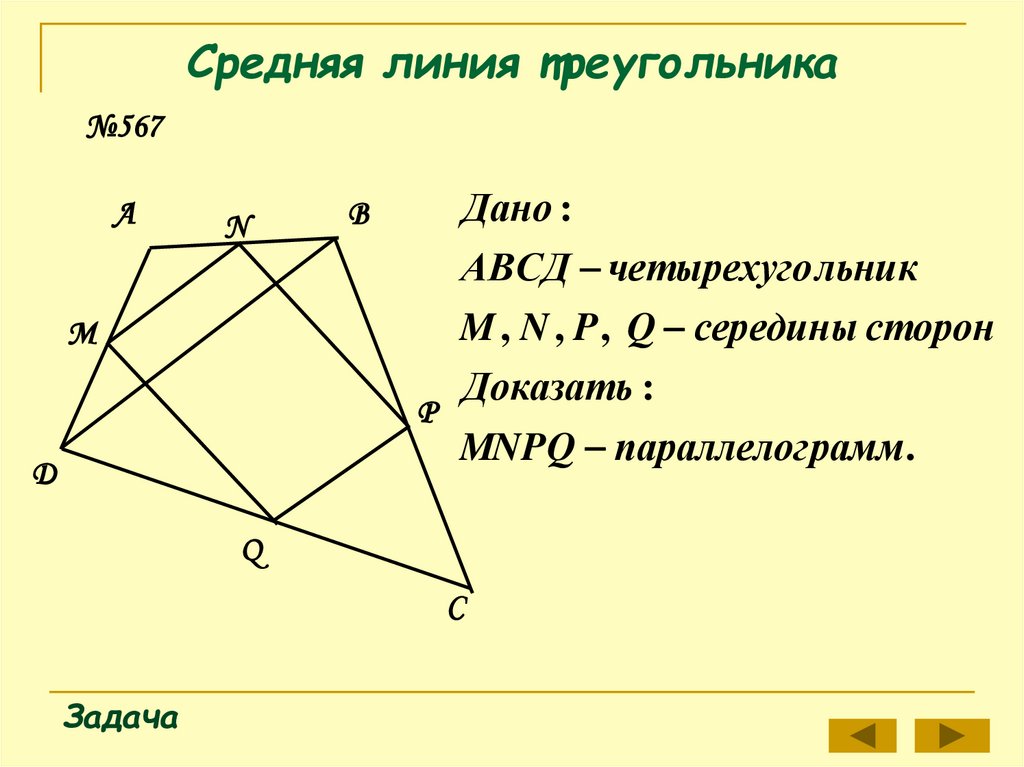
№567
А
N
Дано :
В
АВСД четырехуго льник
M , N , P , Q середины сторон
М
Р
Д
Доказать :
MNPQ параллелог рамм.
Q
С
Задача

8. Средняя линия треугольника

№567
А
N
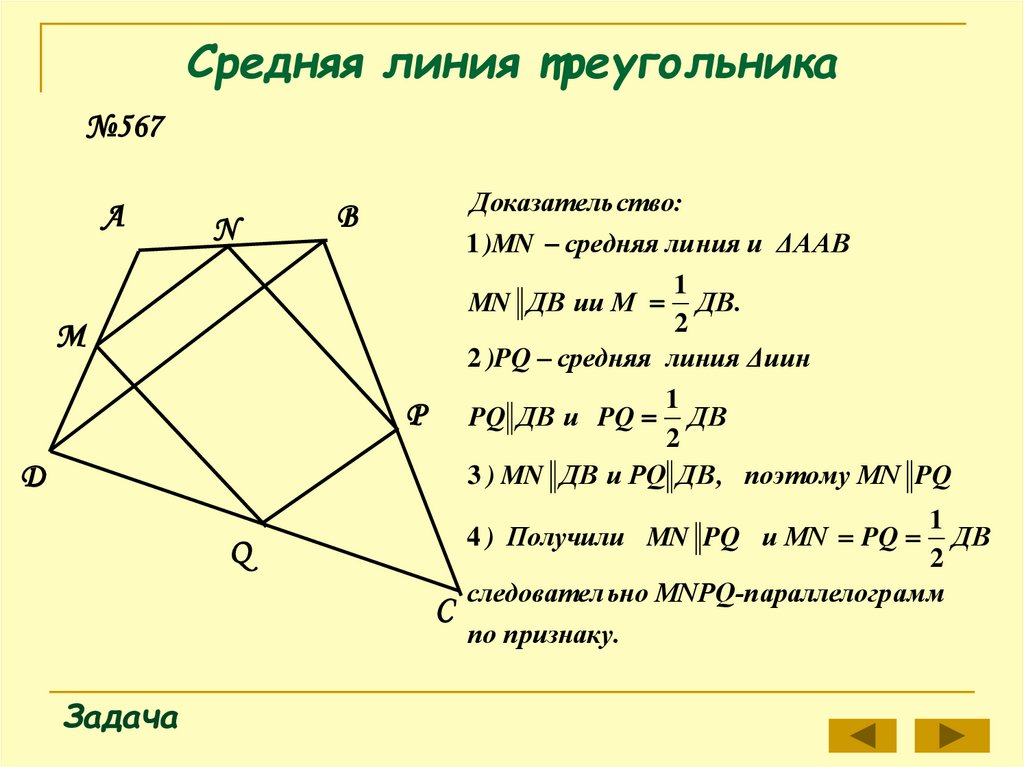
Доказатель ство:
В
1 )MN средняя ли ния и ΔААВ
1
ДВ.
2
2 )PQ средняя линия Δиин
MN ДВ ии M
М
1
ДВ
2
3 ) MN ДВ и PQ ДВ , поэтому MN PQ
Р
PQ ДВ и PQ
Д
Q
С
Задача
1
ДВ
2
следовател ьно MNPQ-п араллелогр амм
4 ) Получили MN PQ и MN PQ
по признаку.

9. Свойство медиан треугольника

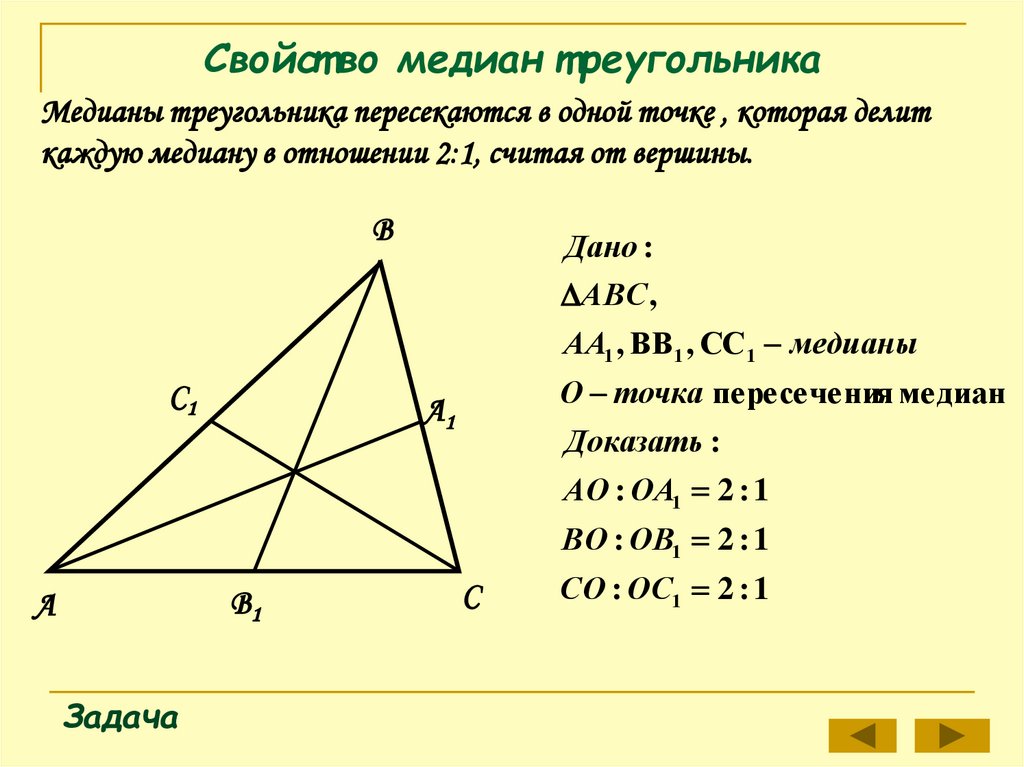
Свойст во медиан т реугольника
Медианы треугольника пересекаются в одной точке , которая делит
каждую медиану в отношении 2:1, считая от вершины.
В
Дано :
АВС ,
АА1 , ВВ1 , СС 1 медианы
C1
О точка пересечения медиан
А1
Доказать :
АО : ОА1 2 : 1
ВО : ОВ1 2 : 1
В1
А
Задача
С
СО : ОС1 2 : 1

10. Свойство медиан треугольника

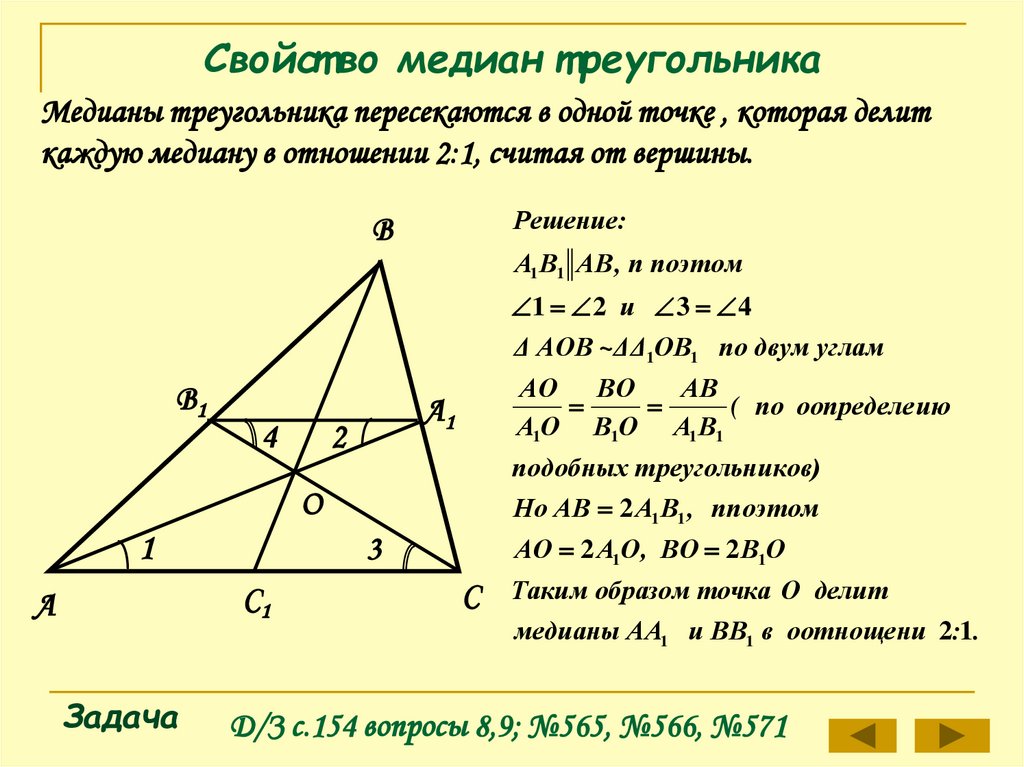
Свойст во медиан т реугольника
Медианы треугольника пересекаются в одной точке , которая делит
каждую медиану в отношении 2:1, считая от вершины.
Решение:
В
А1 В1 АВ , п поэтом
1 2 и 3 4
Δ АОВ ~ΔΔ1ОВ1 по двум углам
В1
4
АО ВО
АВ
( по оопределе ию
А1О В1О А1 В1
А1
2
подобных т реугольников)
О
1
Задача
АО 2 А1О, ВО 2 В1О
3
C1
А
Но АВ 2 А1 В1 , ппоэтом
С
Таким образом точка О делит
медианы АА1 и ВВ1 в оотнощени 2:1.
Д/З с.154 вопросы 8,9; №565, №566, №571

11. Применение подобия к решению задач

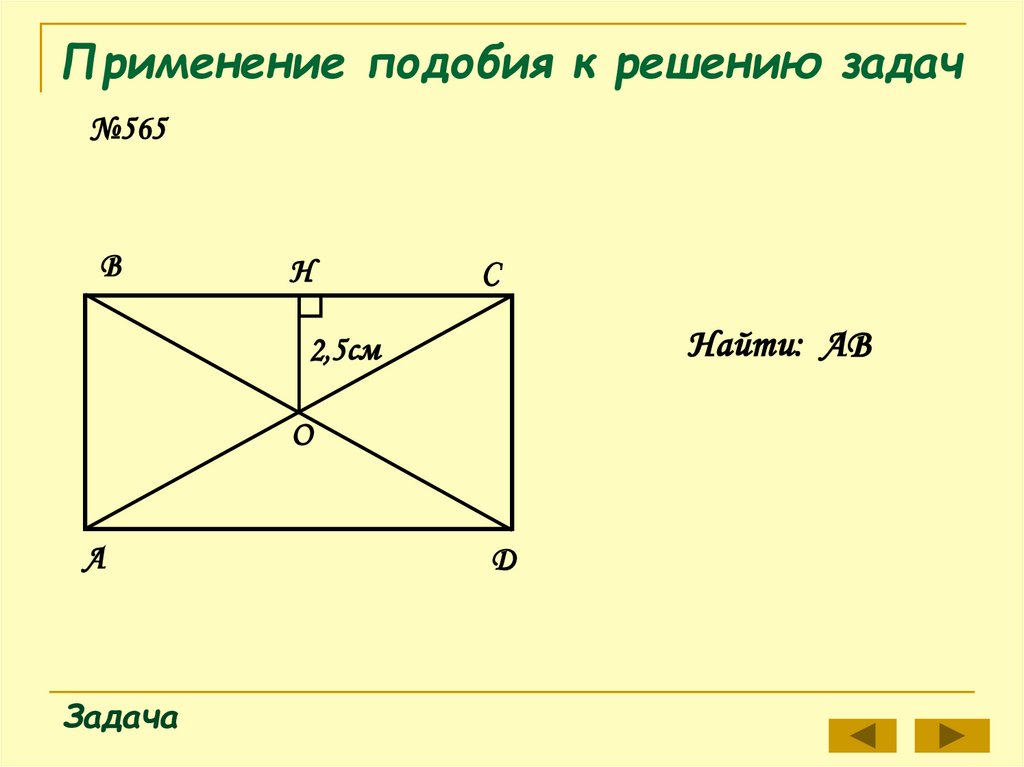
№565
В
Н
С
Найти: АВ
2,5см
О
А
Задача
Д

12. Применение подобия к решению задач

№566
Дано :
В
АВС
АР РВ, AQ QC
Р
PAPQ 21см
Найти : РАВС
А
Q
Задача
С

13. Применение подобия к решению задач

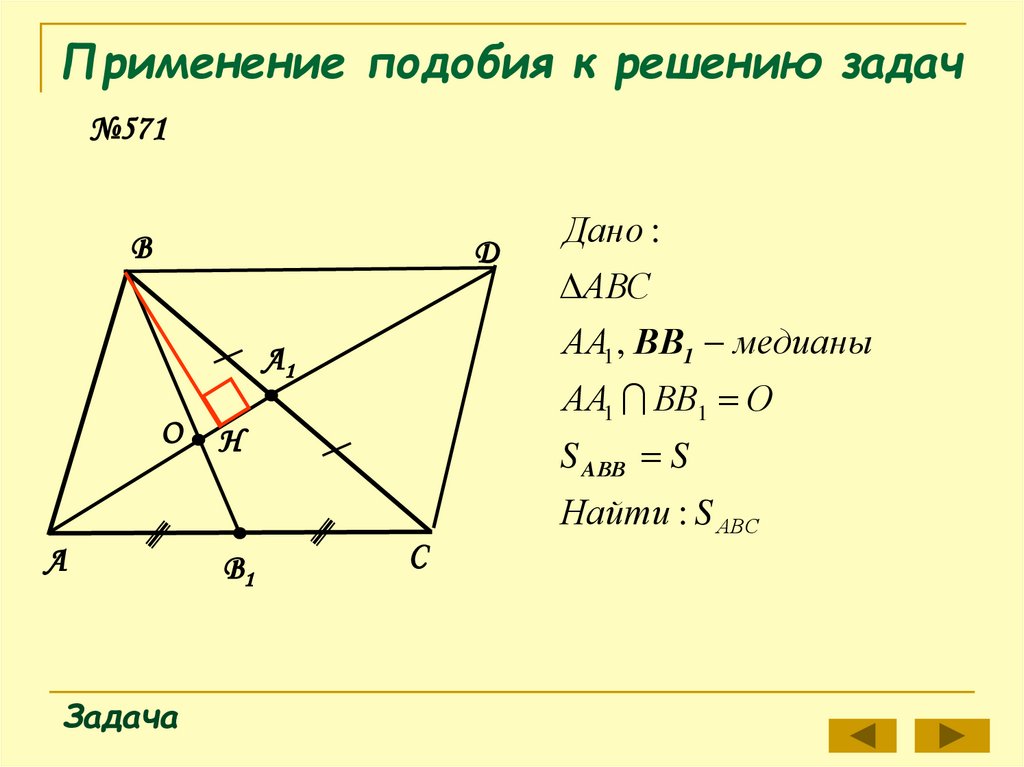
№571
В
Д
А
Задача
АА1 ВВ1 О
Н
В1
АВС
АА1 , ВВ1 медианы
А1
О
Дано :
S AВВ S
С
Найти : S АВС

14. Применение подобия к решению задач

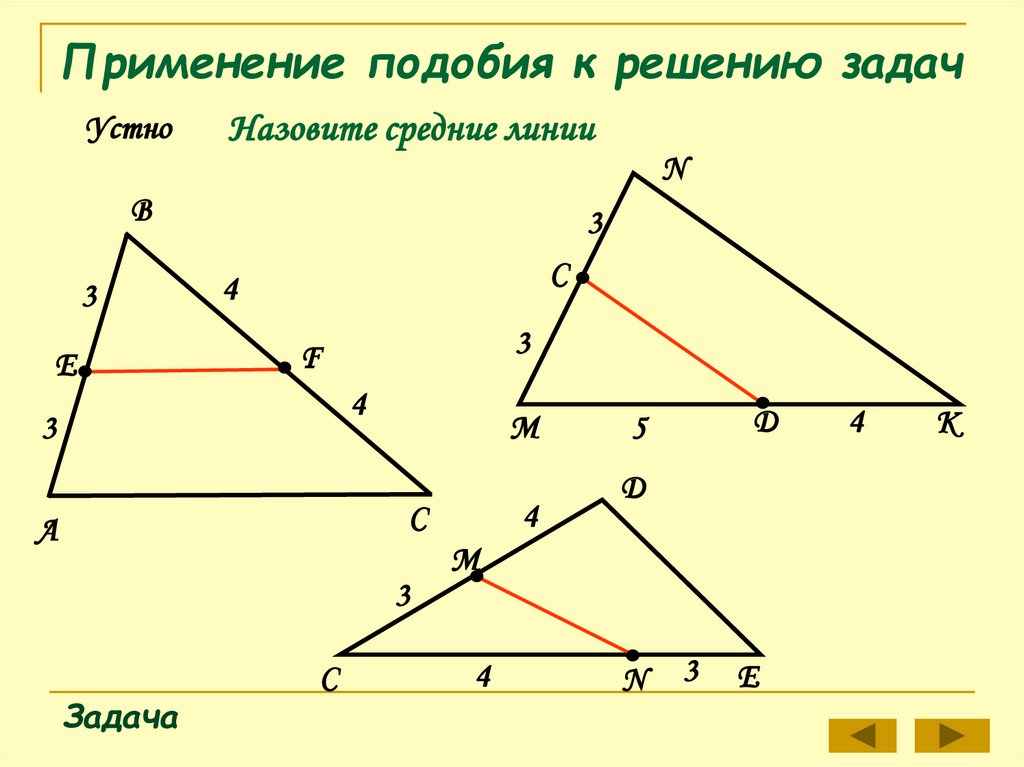
Устно
Назовите средние линии
N
В
3
Е
3
C
4
3
F
4
3
M
4
С
А
3
Задача
C
D
5
D
M
4
N
3
E
4
K

15. Применение подобия к решению задач

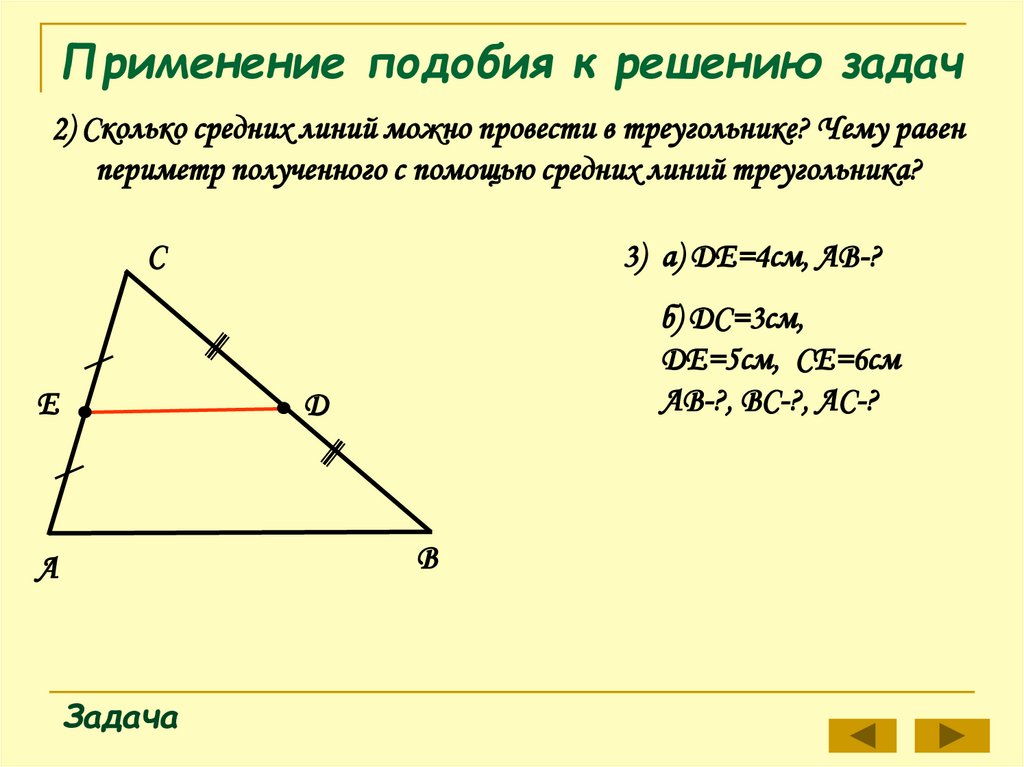
2) Сколько средних линий можно провести в треугольнике? Чему равен
периметр полученного с помощью средних линий треугольника?
С
Е
3) а) ДЕ=4см, АВ-?
б) ДС=3см,
ДЕ=5см, СЕ=6см
АВ-?, ВС-?, АС-?
Д
В
А
Задача

16. Применение подобия к решению задач

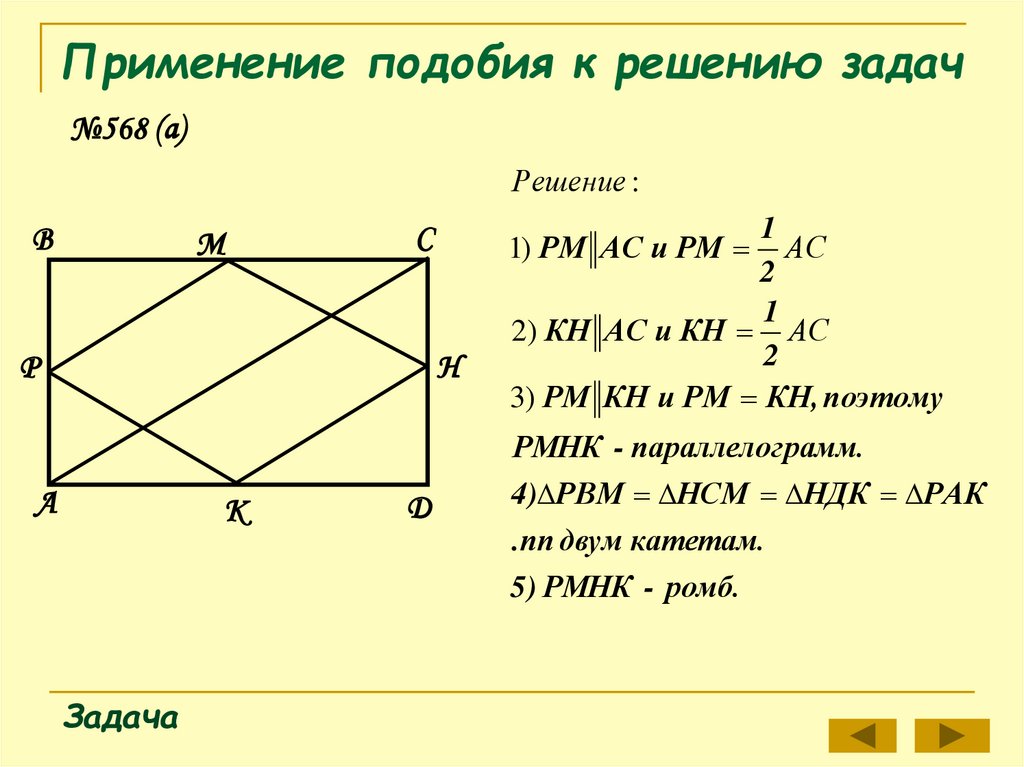
№568 (а)
Решение :
В
М
С
Р
1
АС
2
1
2) КН АС и КН АС
2
3) РМ КН и РМ КН, поэтому
1) РМ АС и РМ
H
РМНК - параллелог рамм.
А
К
Д
4) РВМ НСМ НДК РАК
.пп двум катетам.
5) РМНК - ромб.
Задача

17. Применение подобия к решению задач

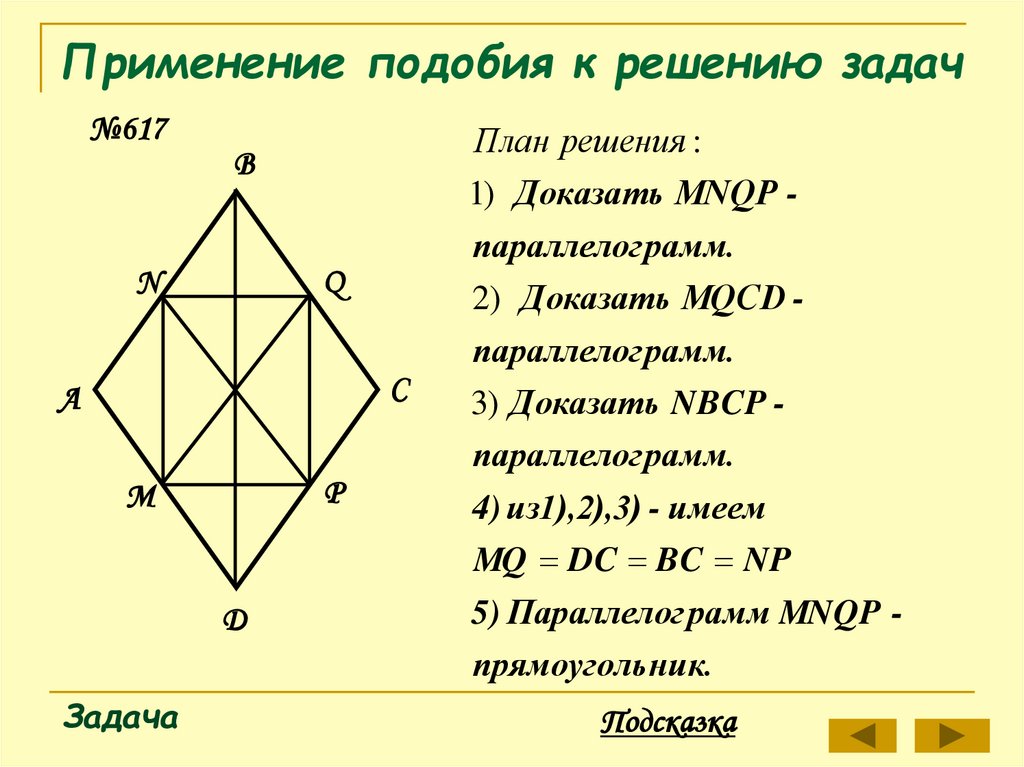
№617
План решения :
В
1) Доказать МNQP параллелог рамм.
Q
N
2) Доказать МQCD параллелог рамм.
C
А
3) Доказать NBCP параллелог рамм.
Р
M
4) из1),2),3) - имеем
MQ DC BC NP
Д
5) Параллелог рамм MNQP прямоуголь ник.
Задача
Подсказка

18. Применение подобия к решению задач

№617
В
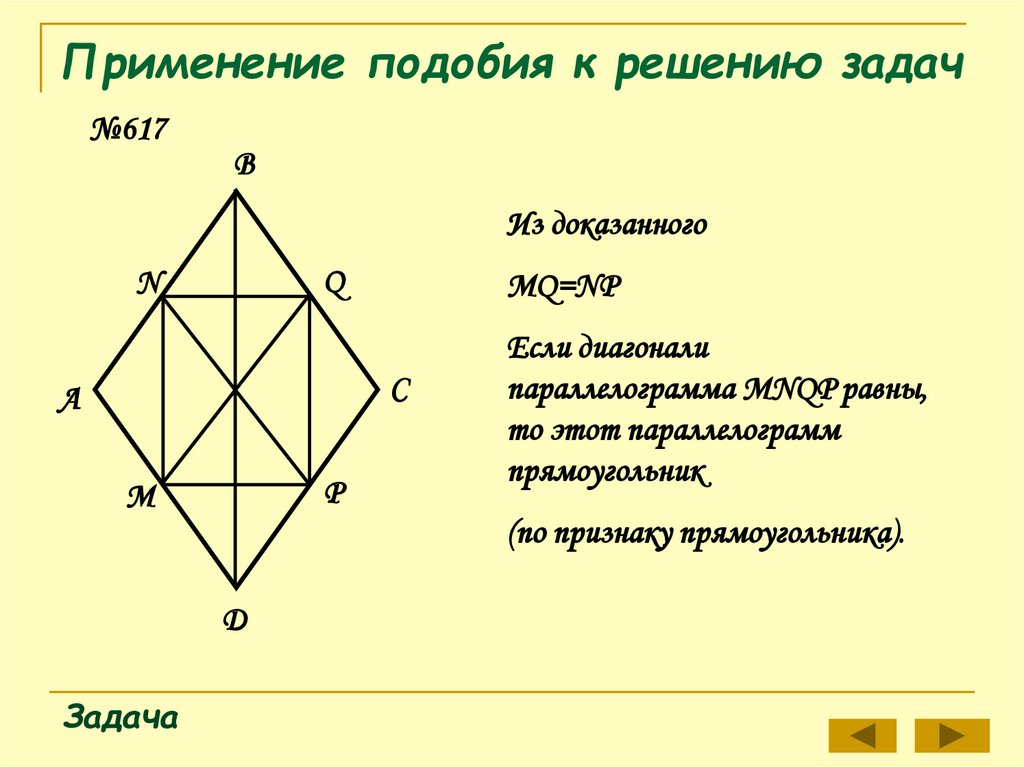
Из доказанного
Q
N
МQ=NP
C
А
Р
M
Если диагонали
параллелограмма MNQP равны,
то этот параллелограмм
прямоугольник
(по признаку прямоугольника).
Д
Задача

19. Применение подобия к решению задач

I вариант
Площадь ромба 48 см2.
Найти площадь
четырехугольника,
вершинами которого
являются середины сторон
данного ромба.
Самост оят ельная работ а
II вариант
Площадь прямоугольника
равна 36 см2. Найти
площадь четырехугольника,
вершинами которого
являются середины сторон
данного прямоугольника.
Д/З №568(б), №618

20.

Литература
Л.С. Атанасян «Геометрия7-9» М., Просвещение,
2002.
Т.Л. Афанасьева, Л.А. Тапилина Геометрия. 8
класс: Поурочные планы по учебнику Л.С. Атанасяна
и др. «Геометрия7-9»