Цилиндр. Виды цилиндра

1.

Учитель математики И.Н. Горбачева
Санкт-Петербург 2014

2.

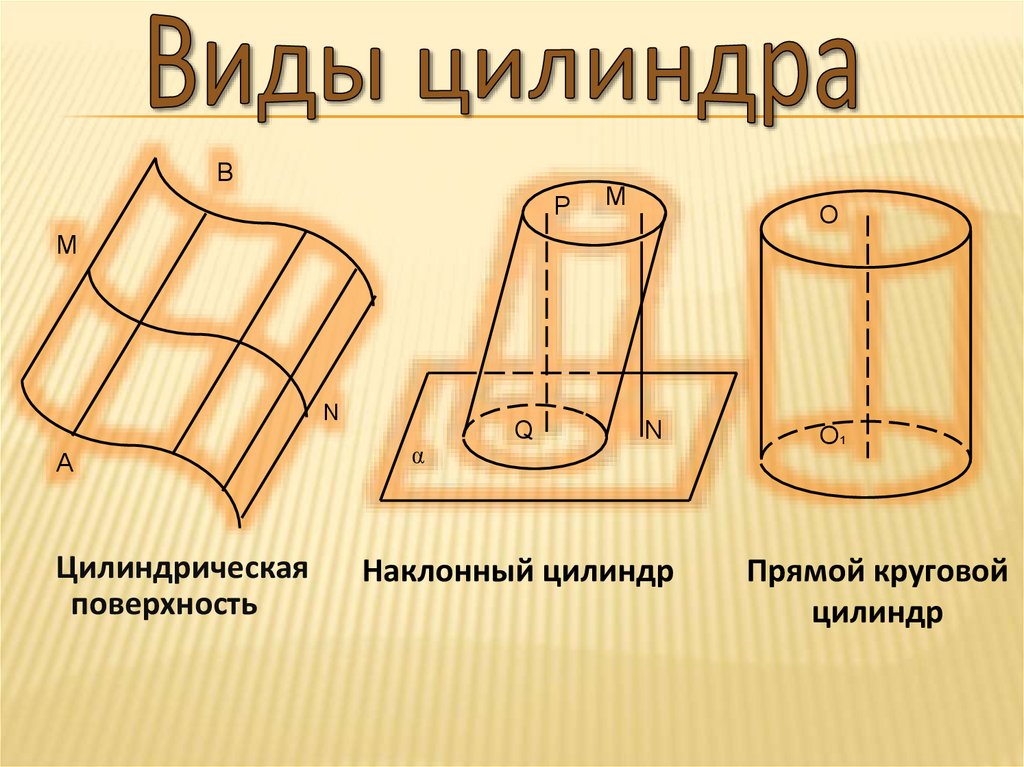
Виды цилиндра
Свойства цилиндров
Цилиндры вокруг нас
Прямой цилиндр. Определение
Элементы цилиндра
Развертка цилиндра
Площадь поверхности цилиндра
Сечения прямого цилиндра
Эллипс как сечение цилиндра
Объем цилиндра
Решение задач

3.

B
P
M
О
M
N
A
Цилиндрическая
поверхность
α
Q
N
Наклонный цилиндр
О1
Прямой круговой
цилиндр

4.

X′
Y′
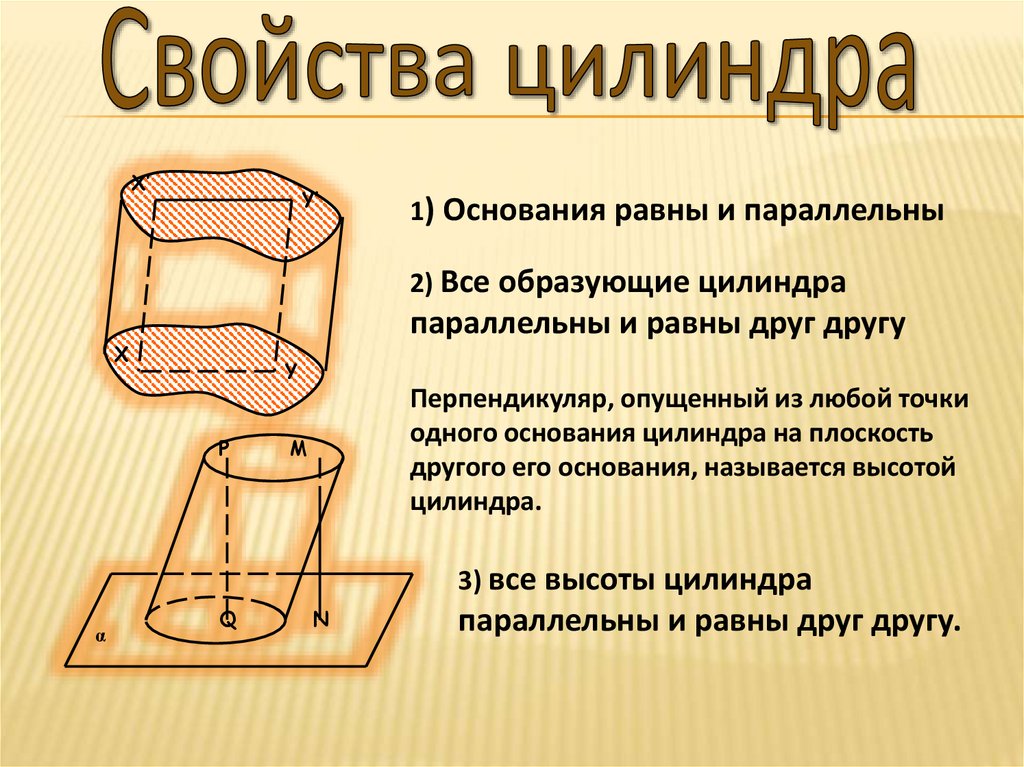
1) Основания равны и параллельны
2) Все образующие цилиндра
параллельны и равны друг другу
X
Y
P
Перпендикуляр, опущенный из любой точки
одного основания цилиндра на плоскость
другого его основания, называется высотой
цилиндра.
M
3) все высоты цилиндра
α
Q
N
параллельны и равны друг другу.

5. Цилиндры вокруг нас

6.

7.

8.

Цили́ндр(др.- греч. κύλινδρος — валик,
каток)
Определение: круговым цилиндром называется тело,
которое состоит из двух кругов, не лежащих в одной
плоскости и совмещаемых параллельным переносом,
и всех отрезков, соединяющих соответствующие точки
этих кругов.
Прямым цилиндр называется, если его образующие
перпендикулярны плоскостям оснований.

9.

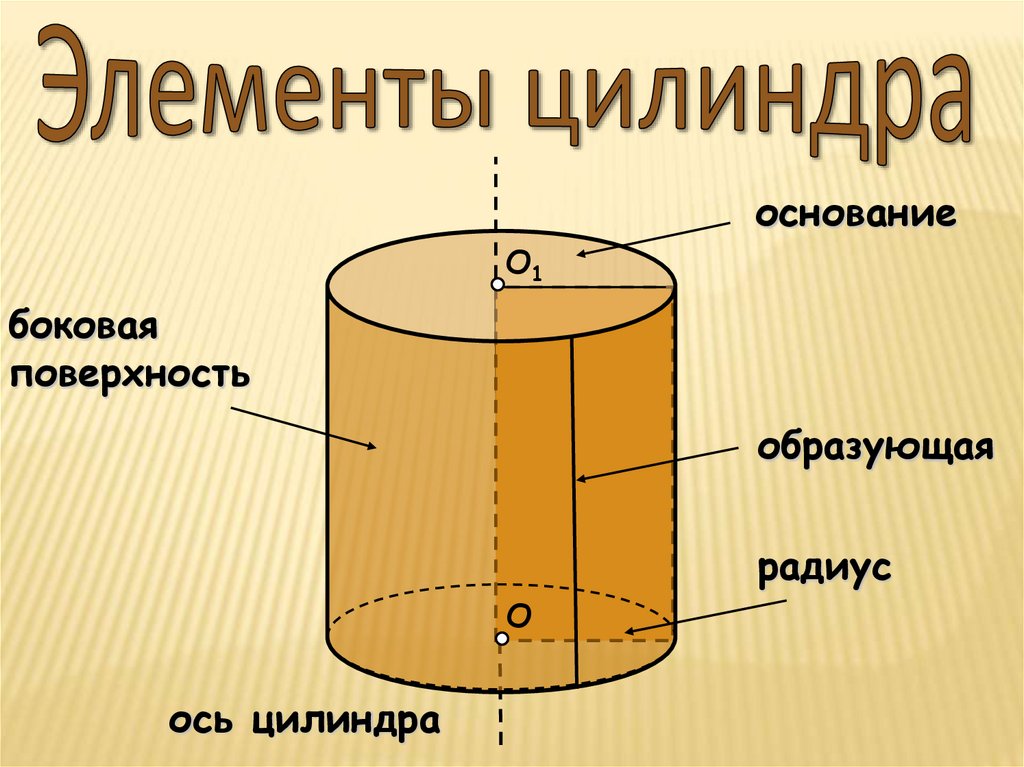
основание
О1
боковая
поверхность
образующая
радиус
О
ось цилиндра

10.

Цилиндр-это тело,
полученное вращением
прямоугольника вокруг
одной из его сторон.
Прямая, содержащая
эту сторону, называется
осью симметрии.

11.

С 2 R
R
О1
О1
H
О
О
R

12.

B
B
h
r
A
B1
h
A1
A
a)
б)
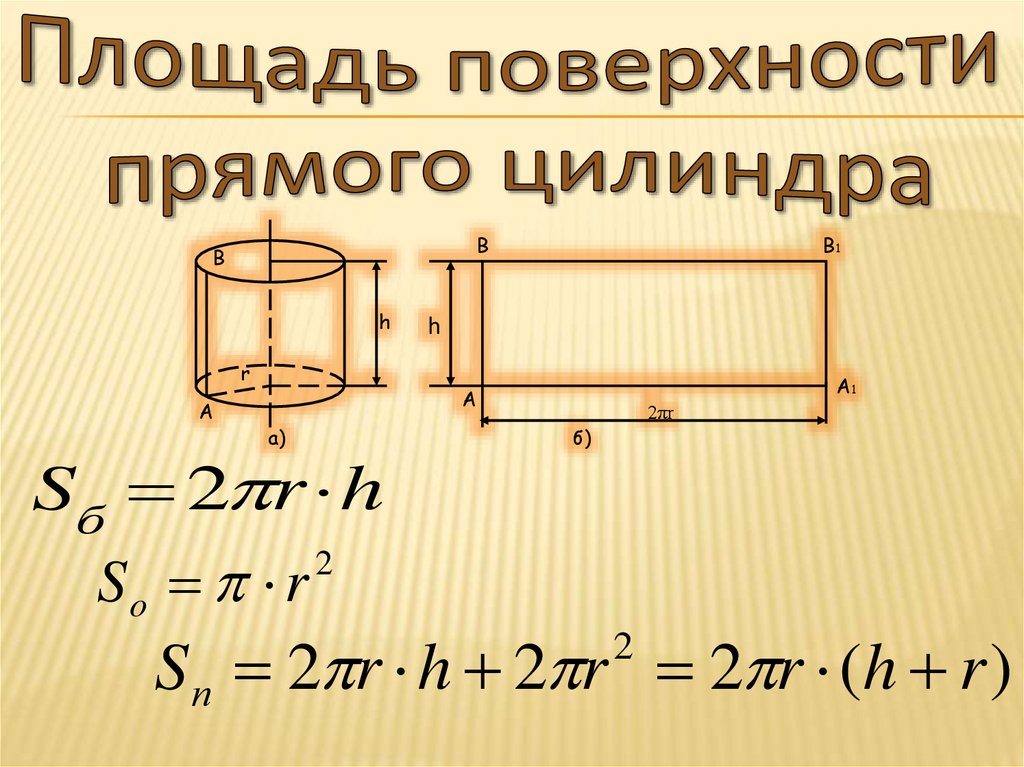
2πr
Sб 2 r h
2
So r
2
S п 2 r h 2 r 2 r (h r )

13.

F′′
F′
F
1) Если секущая плоскость проходит
через ось цилиндра, то сечение
представляет собой прямоугольник ,
две стороны которого –
образующие, а две другие –
диаметры оснований цилиндра.
Такое сечение называется осевым.
α′′
α′
α
2) Все сечения цилиндра
плоскостями параллельными
плоскости основания, равны
основаниям цилиндра между
собой.

14.

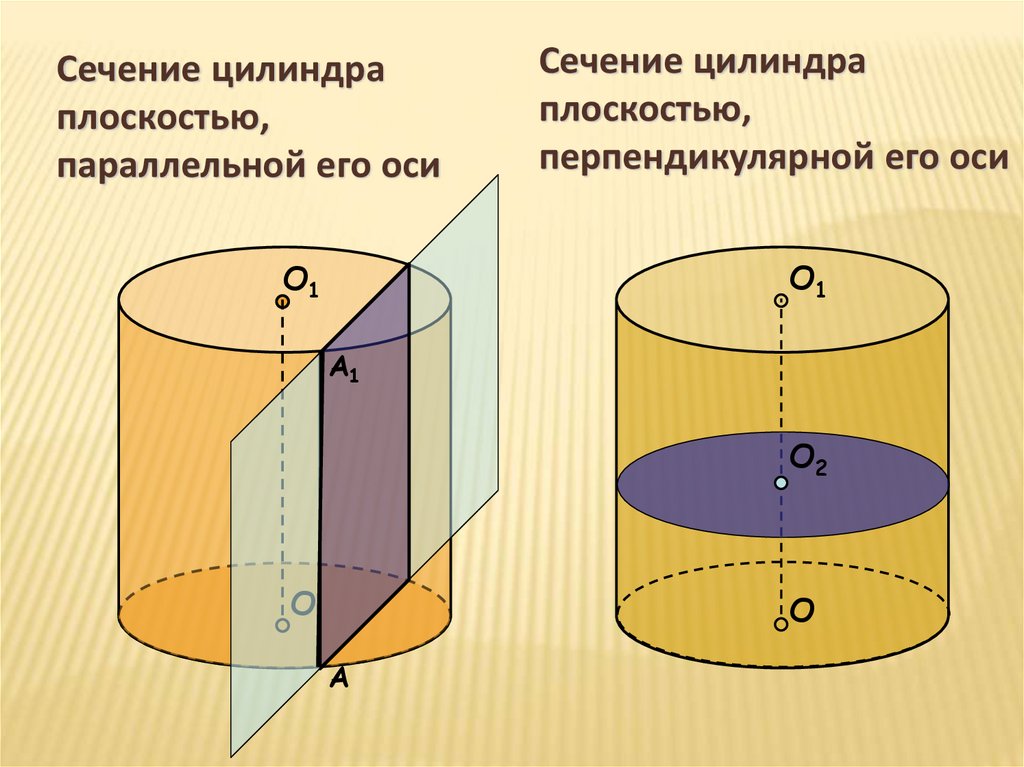
Сечение цилиндра
плоскостью,
параллельной его оси
Сечение цилиндра
плоскостью,
перпендикулярной его оси
О1
О1
А1
О2
О
О
А

15.

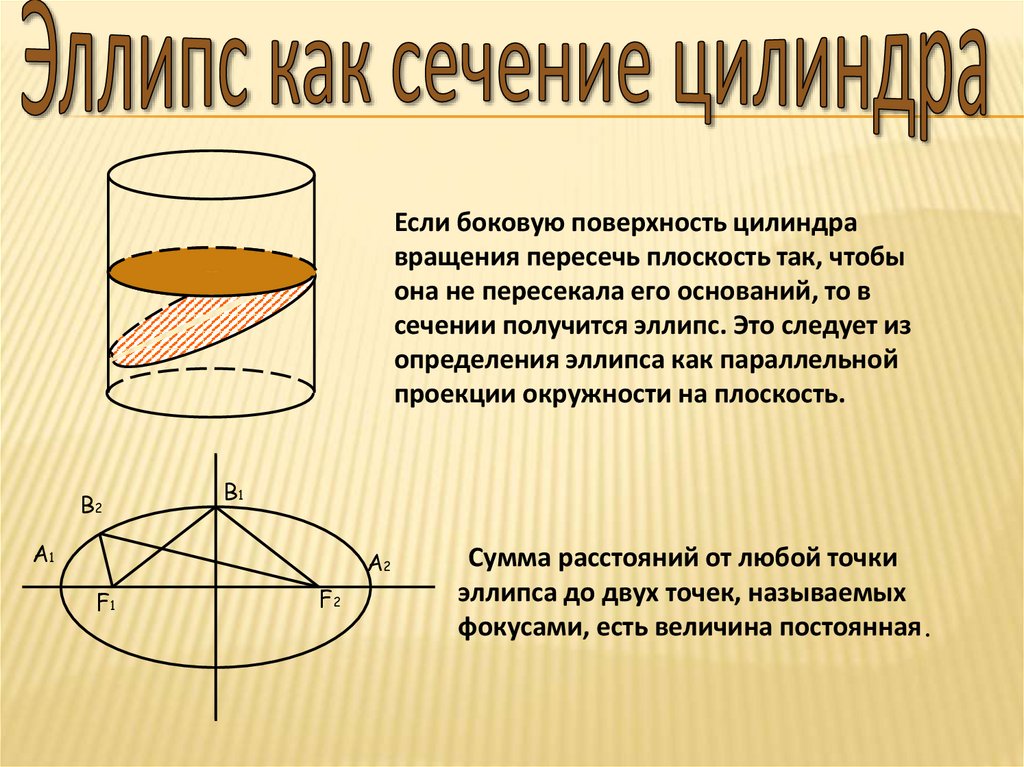
Если боковую поверхность цилиндра
вращения пересечь плоскость так, чтобы
она не пересекала его оснований, то в
сечении получится эллипс. Это следует из
определения эллипса как параллельной
проекции окружности на плоскость.
B2
B1
A1
A2
F1
F2
Сумма расстояний от любой точки
эллипса до двух точек, называемых
фокусами, есть величина постоянная.

16.

h
h
r
h
r
r
Объем цилиндра равен произведению площади
основания на высоту.
V = πr²h

17.

Высота цилиндра равна Н, радиус его основания равен R. В
цилиндр помещена пирамида, высота которой совпадает с
образующей АА1 цилиндра, а основанием служит
равнобедренный треугольник АВС (АВ=АС), вписанный в
основание цилиндра. Найти площадь боковой поверхности
пирамиды и её объём, если А = 120°.
O1
A1
B
D
A
C
O
Дано: цилиндр с высотой H и радиусом
R, вписана пирамида, образующая АА1
– высота пирамиды, АВС р/б, АВ=АС,
АВС – вписан в основание цилиндра,
угол А = 120°.
Найти: Sбок пирамиды, V.

18.

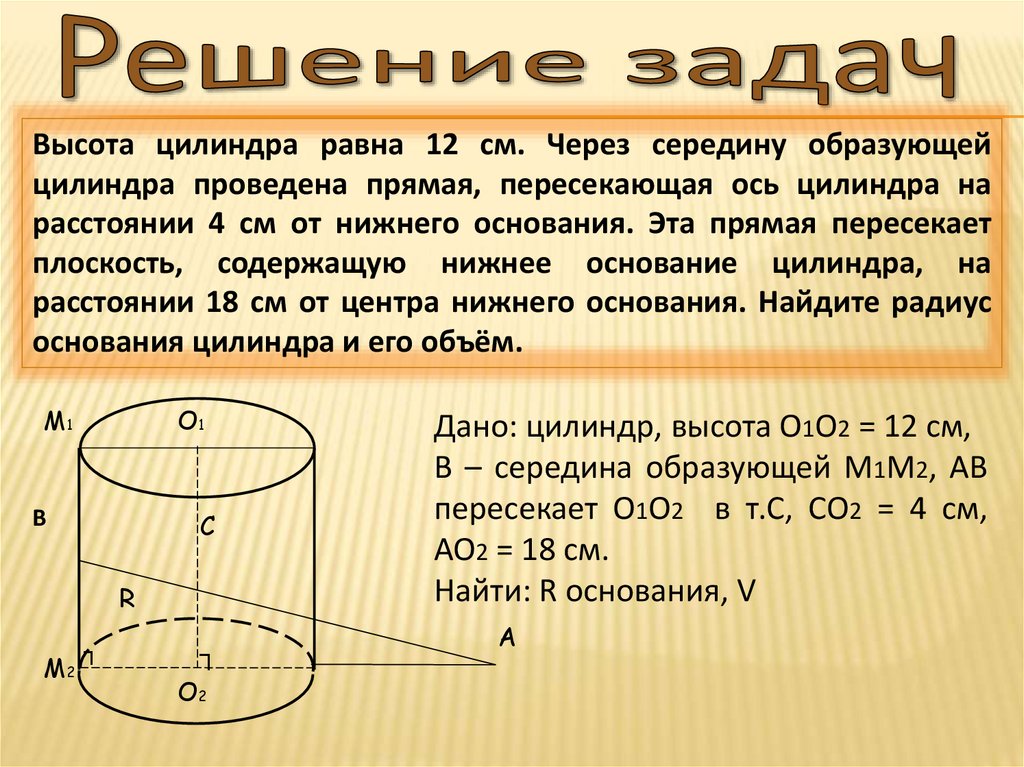
Высота цилиндра равна 12 см. Через середину образующей
цилиндра проведена прямая, пересекающая ось цилиндра на
расстоянии 4 см от нижнего основания. Эта прямая пересекает
плоскость, содержащую нижнее основание цилиндра, на
расстоянии 18 см от центра нижнего основания. Найдите радиус
основания цилиндра и его объём.
M1
O1
B
C
R
М2
┐
┐
O2
Дано: цилиндр, высота О1О2 = 12 см,
В – середина образующей М1М2, АВ
пересекает О1О2 в т.С, СО2 = 4 см,
АО2 = 18 см.
Найти: R основания, V
А