Похожие презентации:
Цилиндр. Виды цилиндра
1.
2.
3.
4. Слово «…?»
происходит от греческого слова«Kylindros» - килиндрос, то
есть «вращаю», «катаю»,
«валик», «свиток» .
Что это за слово?
5.
Тема: Цилиндр6. Задание :
Приведите примерыпредметов имеющих
цилиндрическую
форму
7. Примеры цилиндров
8. ПРИМЕРЫ ЦИЛИНДРА
9.
10.
Цилиндрическая архитектура11. Цилиндр
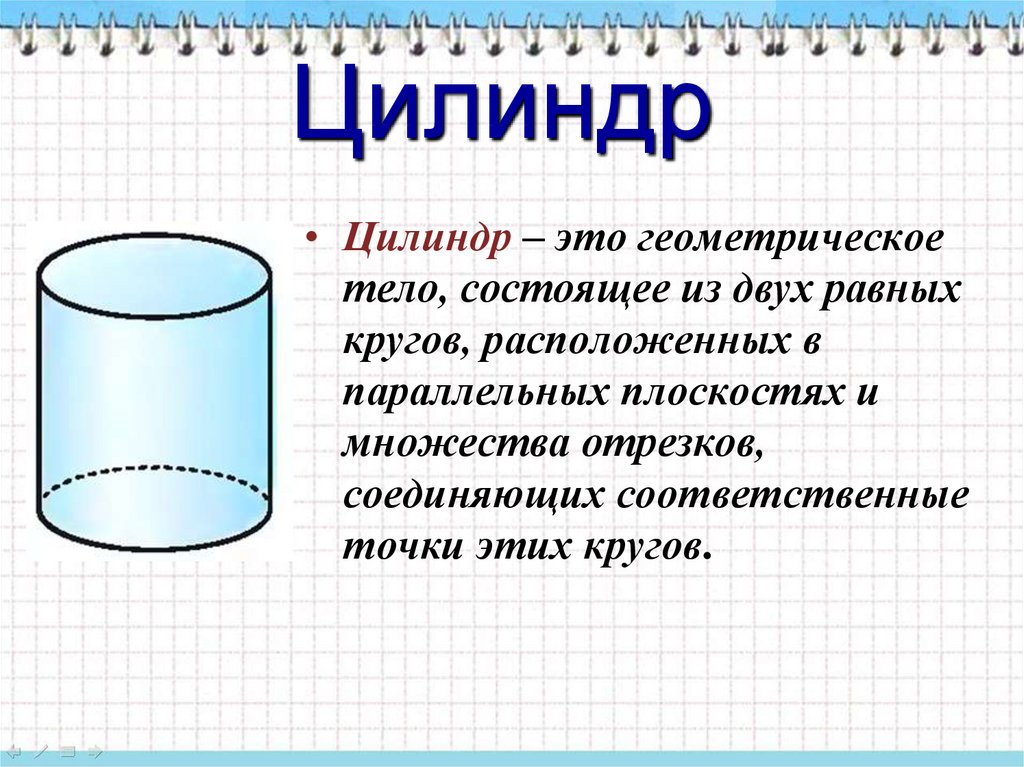
• Цилиндр – это геометрическоетело, состоящее из двух равных
кругов, расположенных в
параллельных плоскостях и
множества отрезков,
соединяющих соответственные
точки этих кругов.
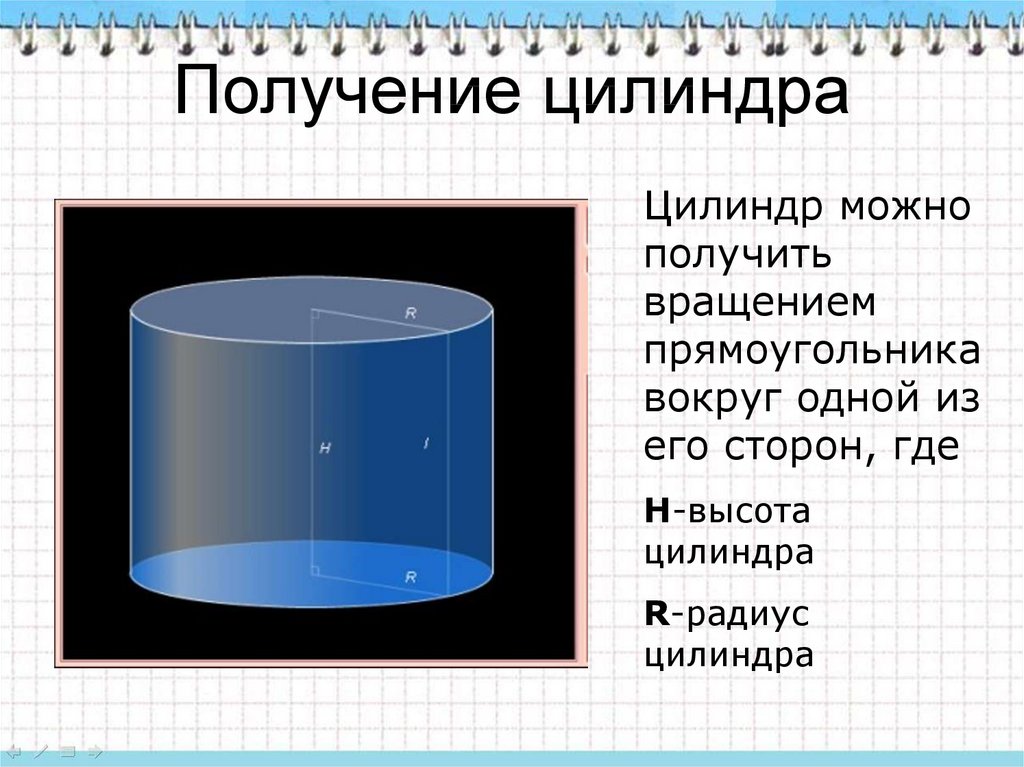
12. Получение цилиндра
Цилиндр можнополучить
вращением
прямоугольника
вокруг одной из
его сторон, где
H-высота
цилиндра
R-радиус
цилиндра
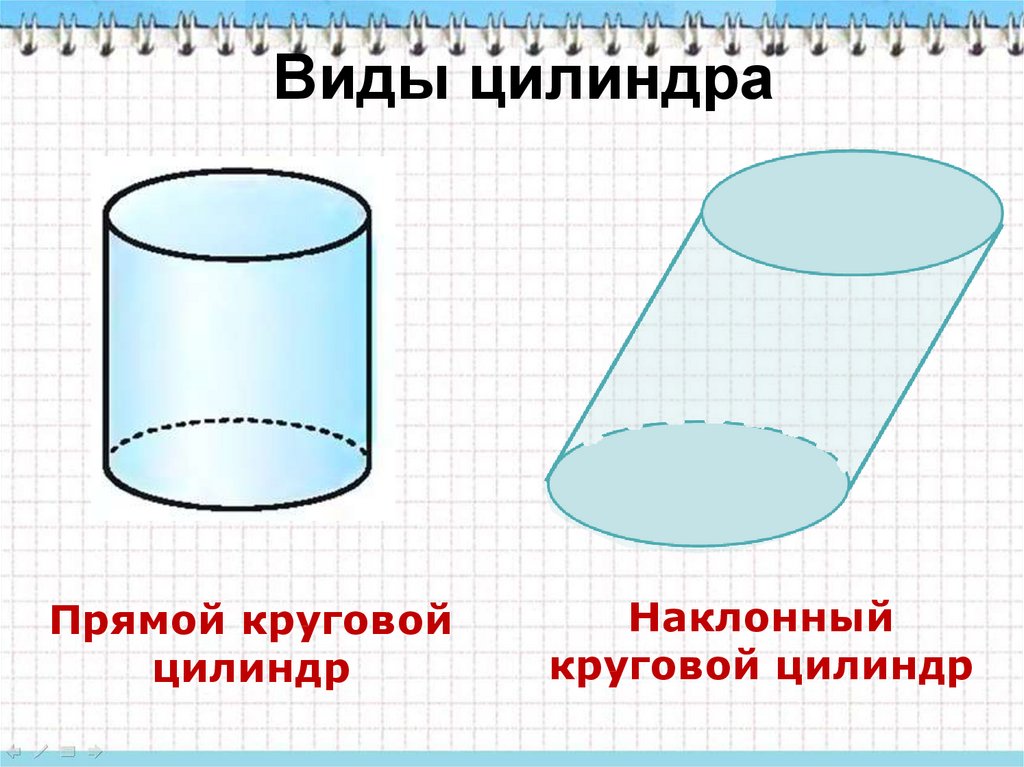
13. Виды цилиндра
Прямой круговойцилиндр
Наклонный
круговой цилиндр
14.
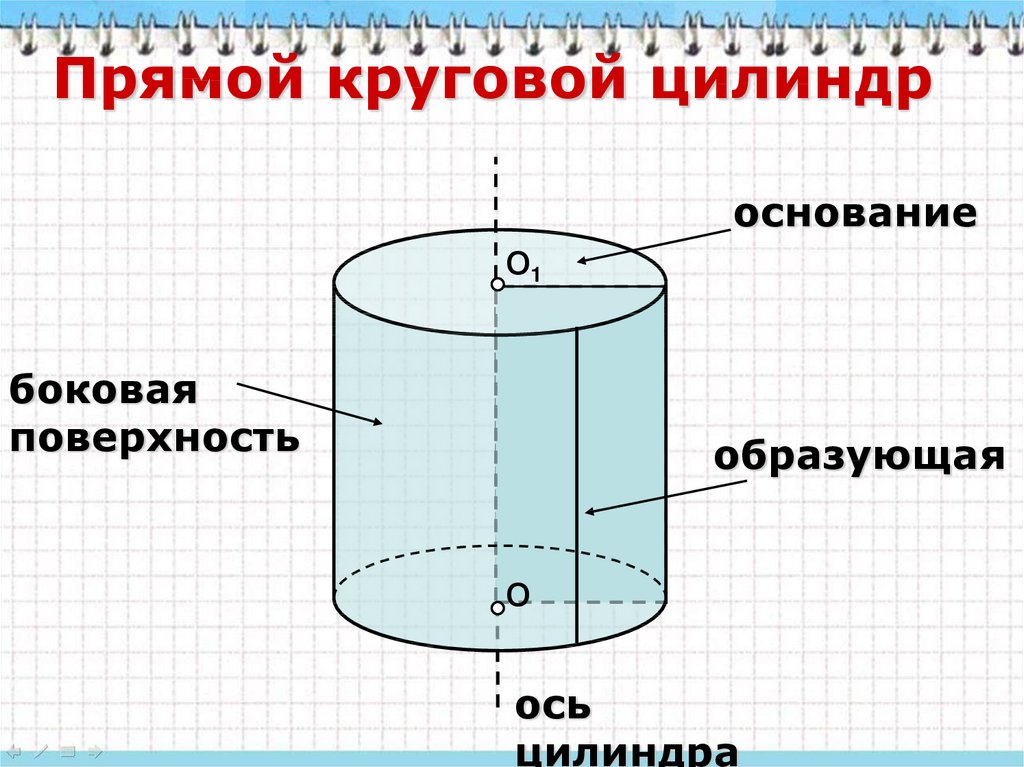
Прямой круговой цилиндроснование
О1
боковая
поверхность
образующая
О
ось
цилиндра
15. Элементы цилиндра
• Основанияцилиндра
–
равные
круги,
расположенные в параллельных плоскостях
• Высота цилиндра - это расстояние между
плоскостями его оснований.
• Радиус цилиндра – это радиус его основания.
• Ось цилиндра – это прямая, проходящая через
центры основания цилиндра (ось цилиндра
является осью вращения цилиндра).
16. Образующая цилиндра - это отрезок соединяющий точку окружности верхнего основания с соответственной точкой окружности нижнего
основания.Все
образующие
параллельны
оси
вращения и имеют одинаковую длину,
равную
высоте
цилиндра.
Образующая цилиндра при вращении
вокруг
оси
образует
боковую
(цилиндрическую) поверхность цилиндра.
17.
18.
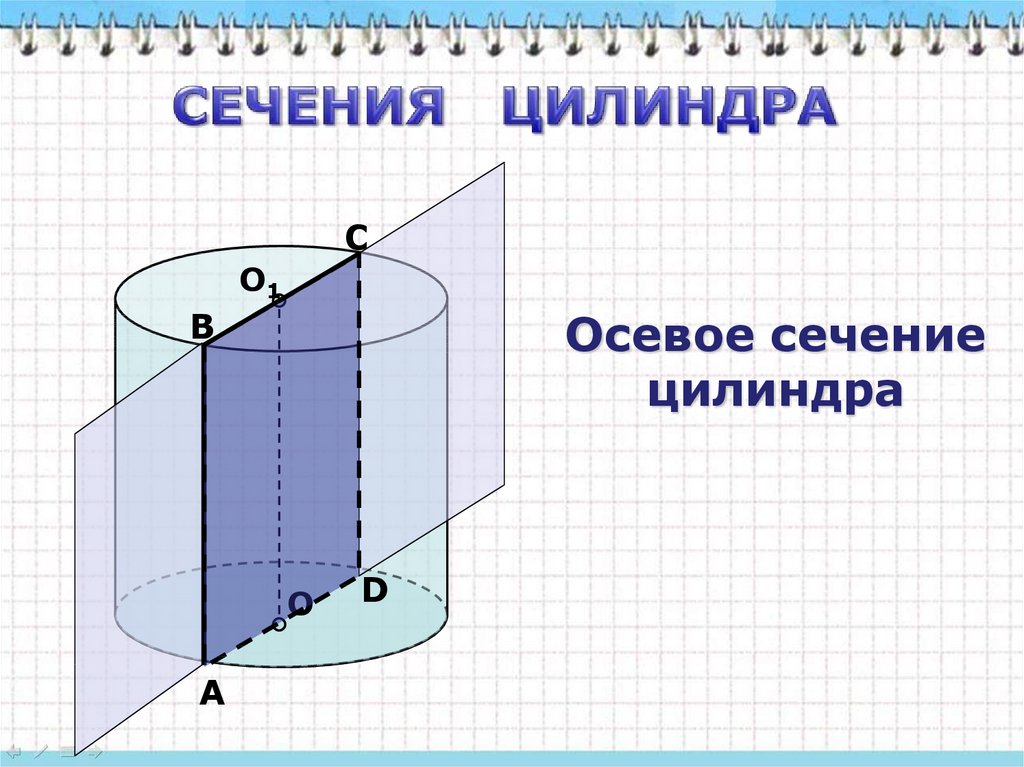
СО1
В
Осевое сечение
цилиндра
О
А
D
19.
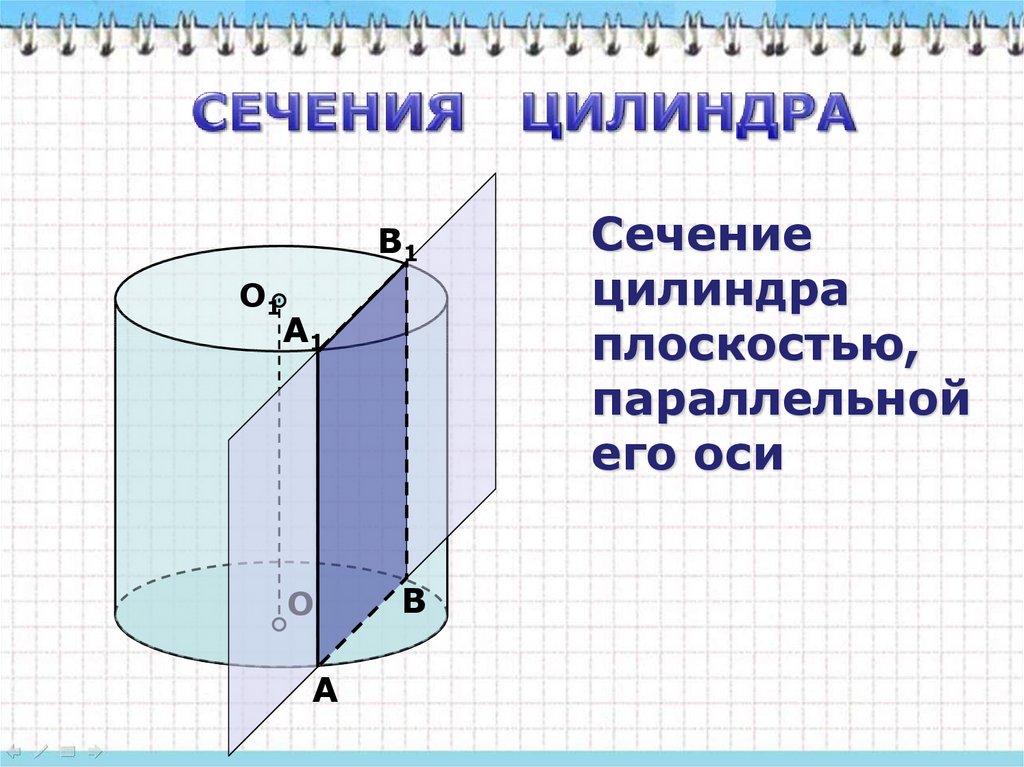
B1О1
А1
О
А
B
Сечение
цилиндра
плоскостью,
параллельной
его оси
20.
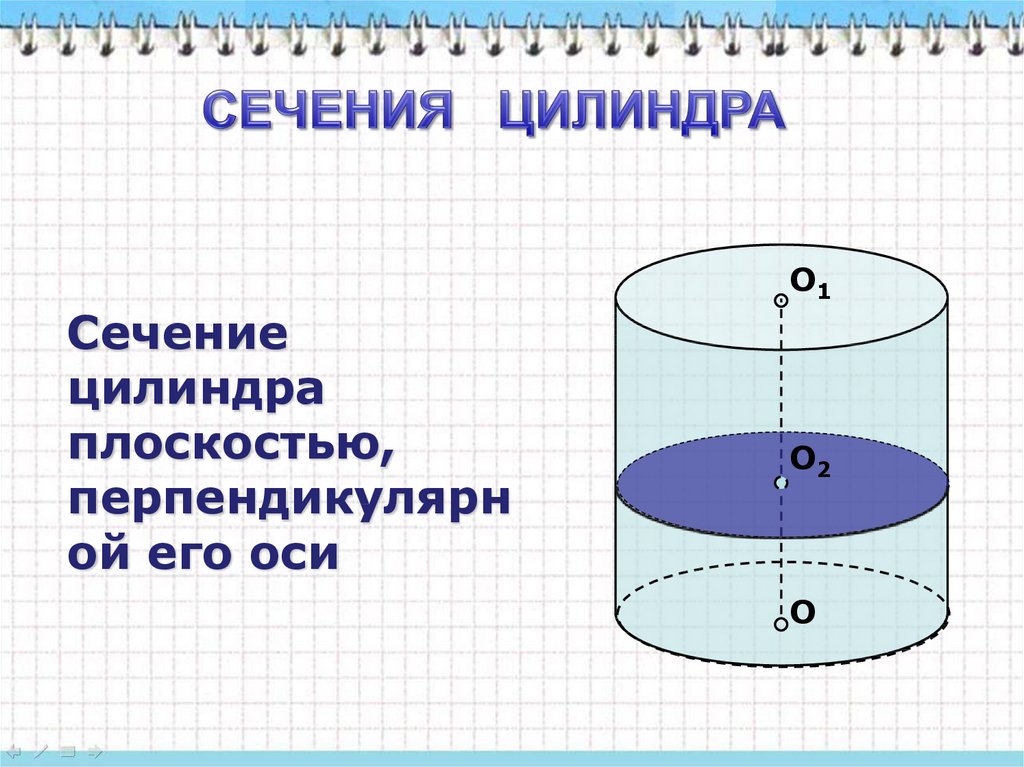
О1Сечение
цилиндра
плоскостью,
перпендикулярн
ой его оси
О2
О
21.
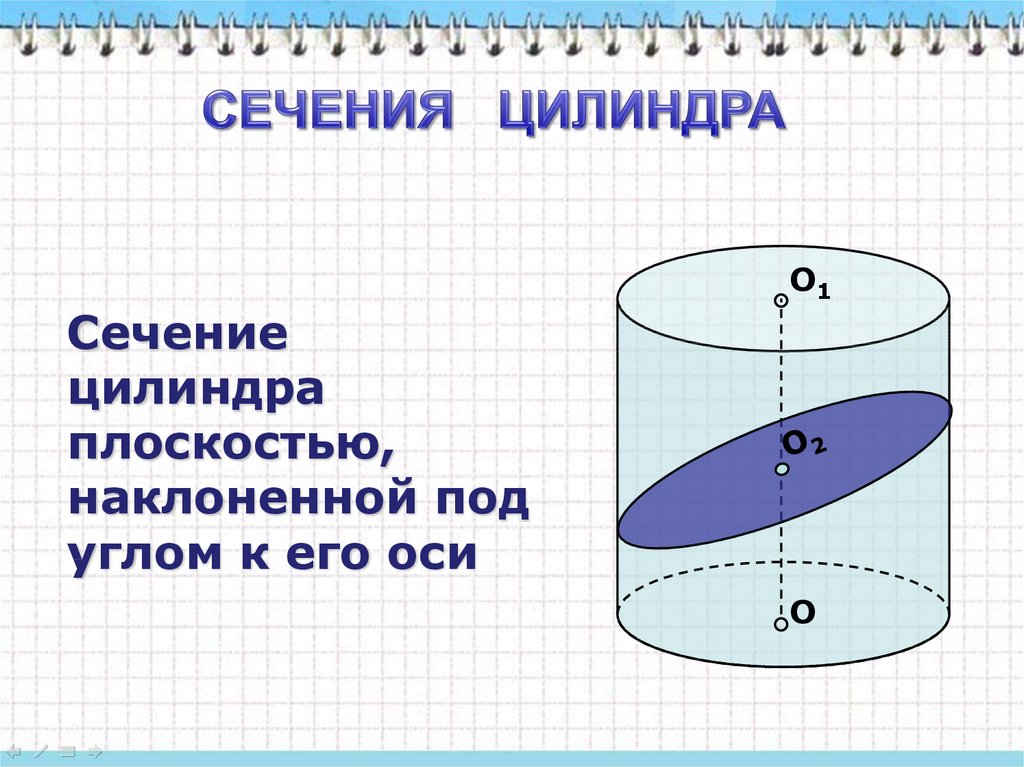
О1Сечение
цилиндра
плоскостью,
наклоненной под
углом к его оси
О
22.
Площадь поверхностицилиндра
С 2 R
R
О1
О1
H
Sосн R
2
Sбок 2 R H
О
S полн 2 R H 2 R 2 R ( H R)
2
О
R
23.
Найдите площадь поверхности (внешней ивнутренней) шляпы, размеры которой (в см)
указаны на рисунке.
Решение.
1) Если дно шляпы опустить на
плоскость её полей, то получим
круг радиуса R = …+… = … cм.
r1=10
10
10
2) Площадь этого круга
Sосн. = …….
3) Найдем площадь боковой поверхности цилиндрической части
Sбок. = ….
4) Найдем площадь шляпы
Sполн. =















 Математика
Математика








