Похожие презентации:
Конические сечения и свойства их касательных
1. Конические сечения и свойства их касательных
2.
3.
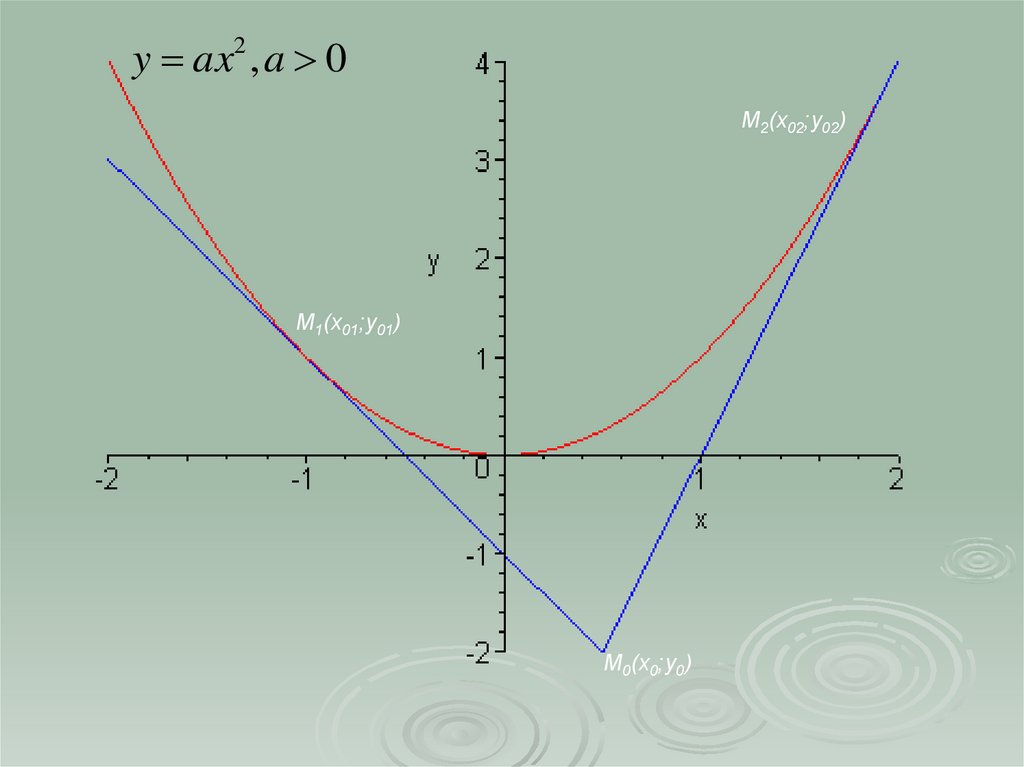
y ax2 , a 0М2(x02;y02)
М1(x01;y01)
М0(x0;y0)
4.
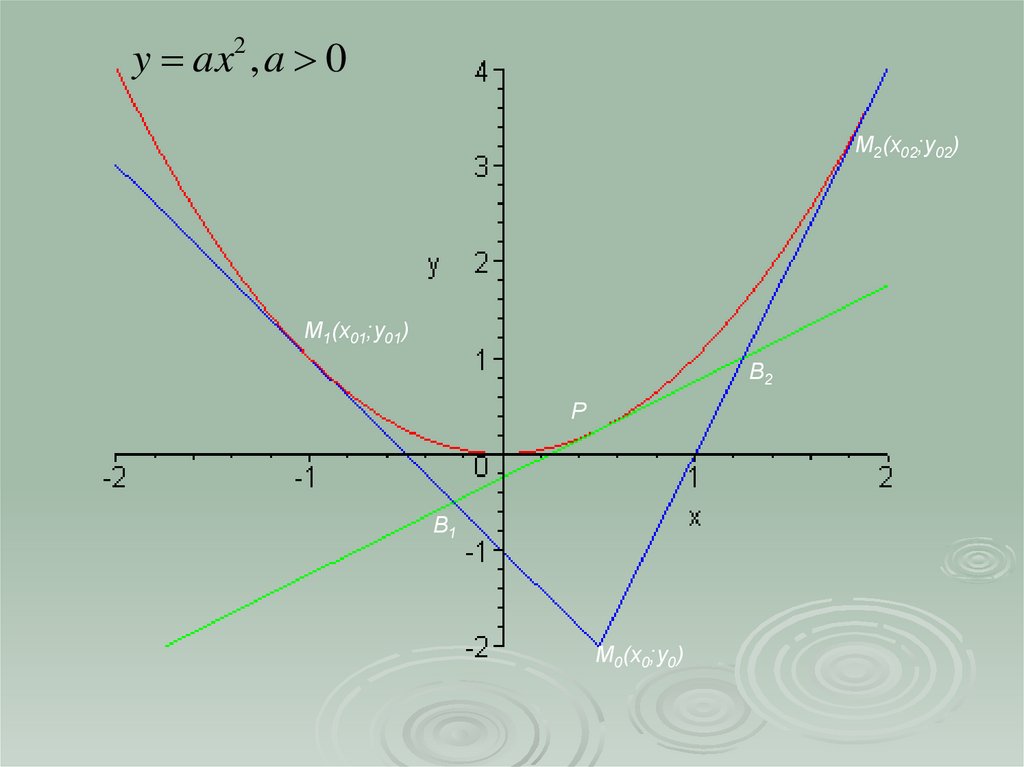
y ax2 , a 0М2(x02;y02)
М1(x01;y01)
B2
P
B1
М0(x0;y0)
5.
Утверждение 1:M 0 B1
M 0 B2
1
M 0M1 M 0M 2
y ax2 , a 0
М2(x02;y02)
М1(x01;y01)
B2
P
B1
М0(x0;y0)
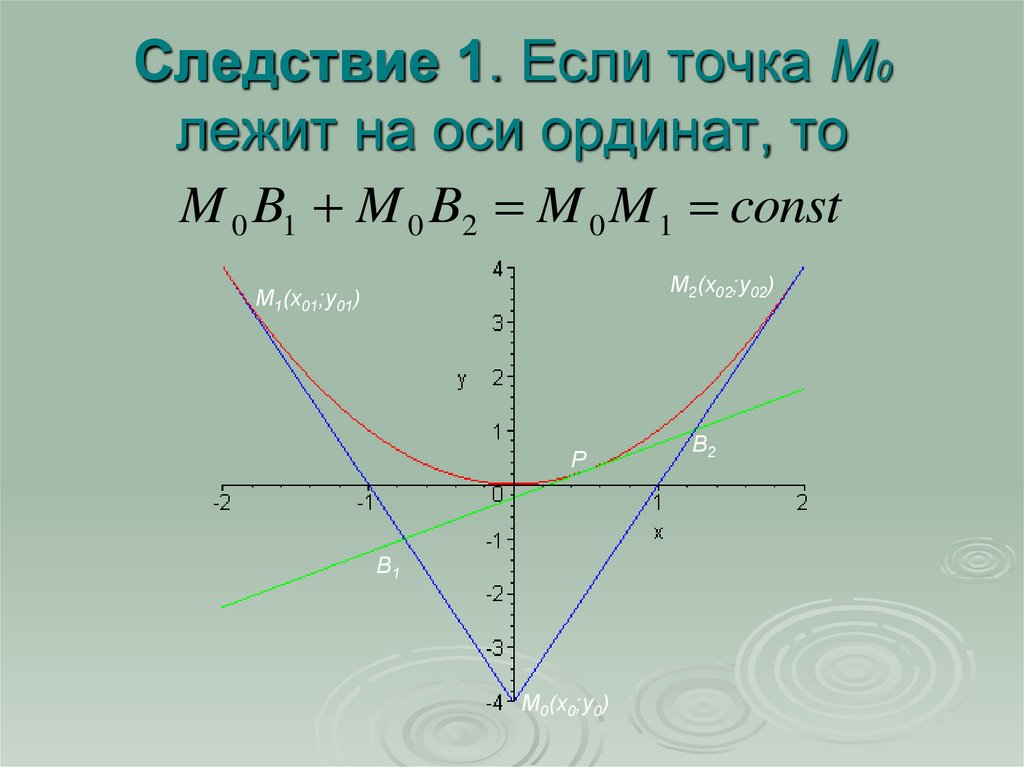
6. Следствие 1. Если точка М0 лежит на оси ординат, то
M 0 B1 M 0 B2 M 0 M 1 constМ2(x02;y02)
М1(x01;y01)
P
B1
М0(x0;y0)
B2
7. Следствие 2. Огибающей семейства прямых
x y1
a b
a b const
является парабола
У
У
О
Х
О
Х
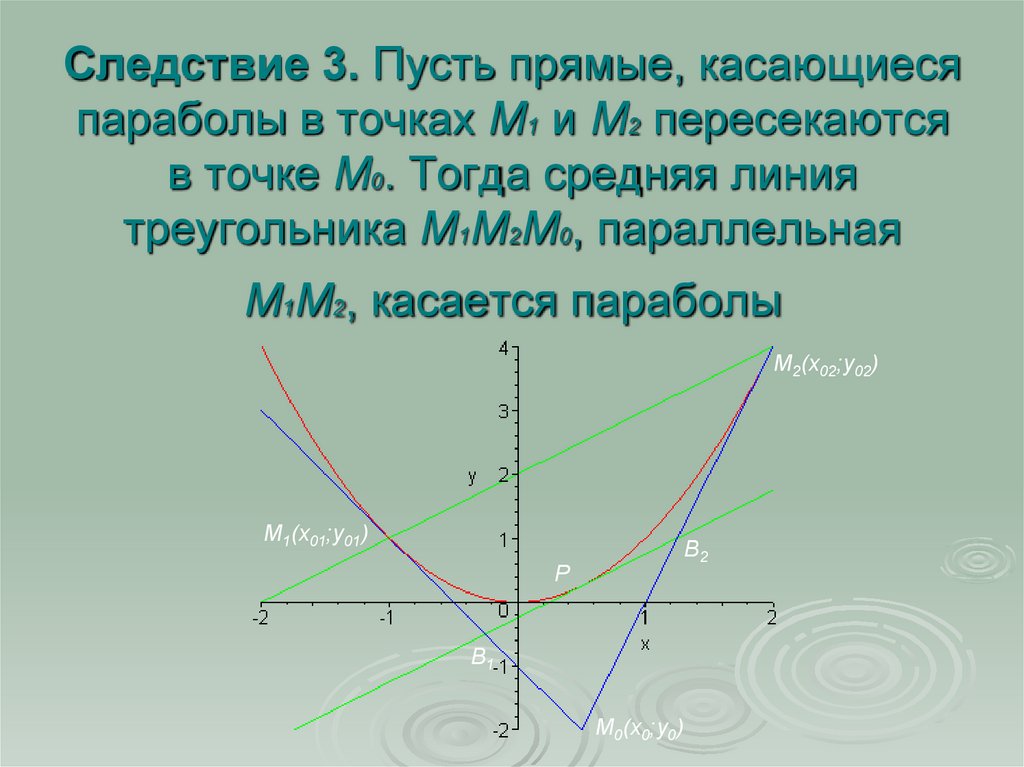
8. Следствие 3. Пусть прямые, касающиеся параболы в точках M1 и M2 пересекаются в точке M0. Тогда средняя линия треугольника
M1M2M0, параллельнаяM1M2, касается параболы
М2(x02;y02)
М1(x01;y01)
B2
P
B1
М0(x0;y0)
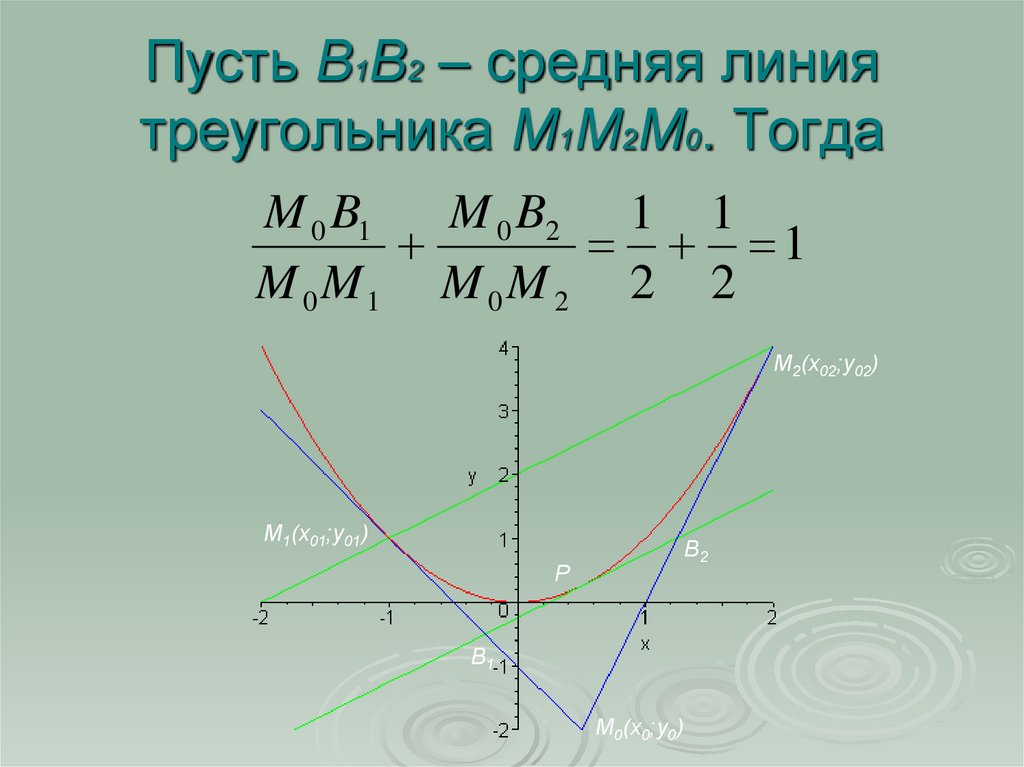
9. Пусть B1B2 – средняя линия треугольника M1M2M0. Тогда
M 0 B1M 0 B2 1 1
1
M 0 M1 M 0 M 2 2 2
М2(x02;y02)
М1(x01;y01)
B2
P
B1
М0(x0;y0)
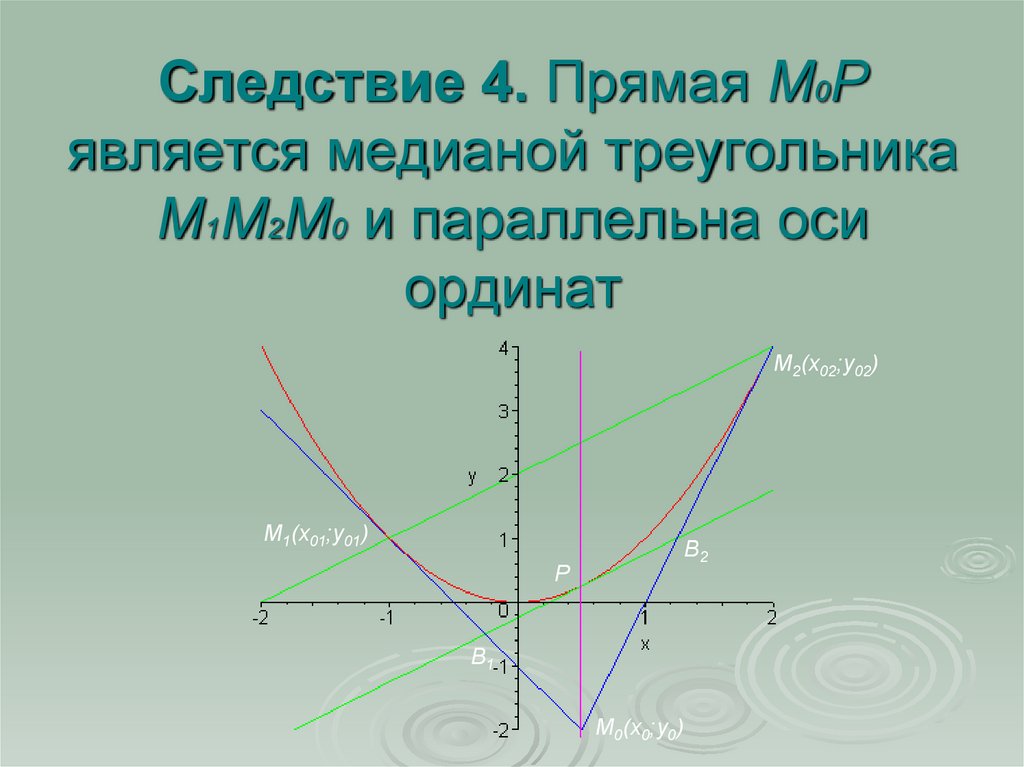
10. Следствие 4. Прямая М0Р является медианой треугольника M1M2M0 и параллельна оси ординат
М2(x02;y02)М1(x01;y01)
B2
P
B1
М0(x0;y0)
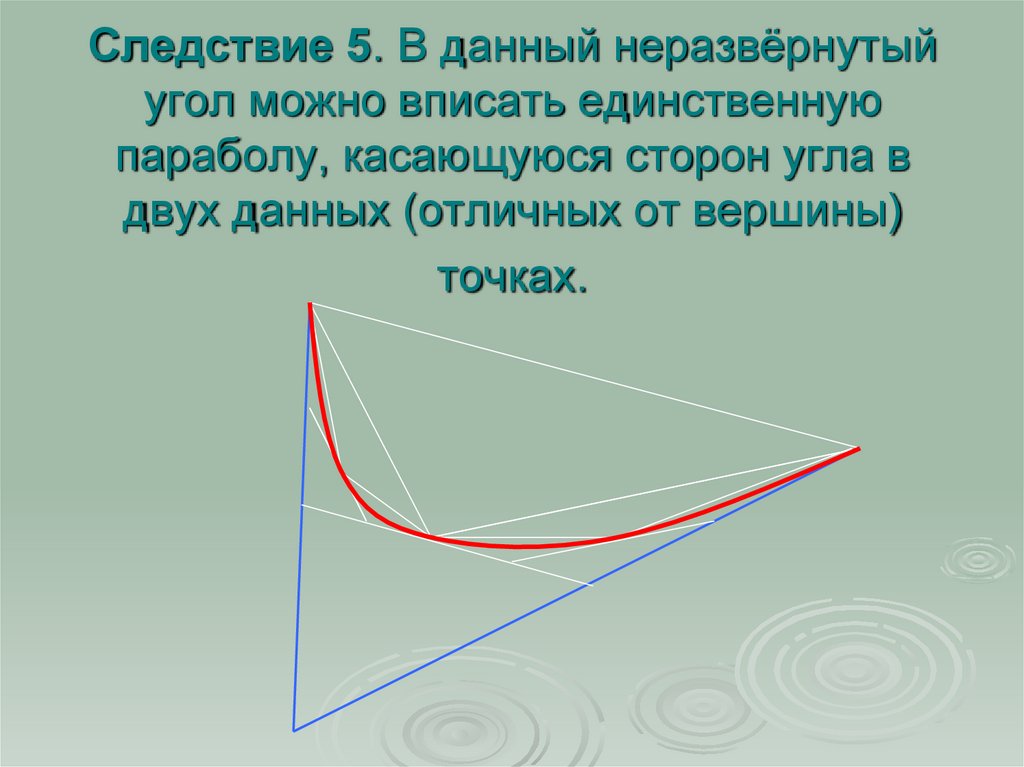
11. Следствие 5. В данный неразвёрнутый угол можно вписать единственную параболу, касающуюся сторон угла в двух данных (отличных от
вершины)точках.
12.
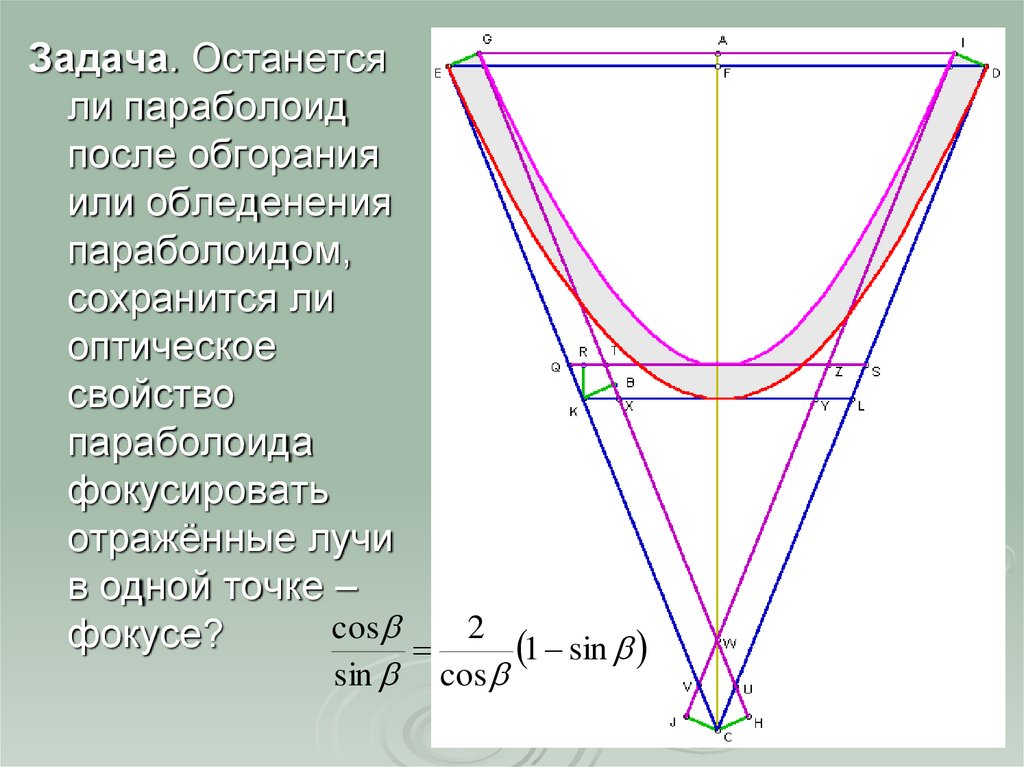
Задача. Останетсяли параболоид
после обгорания
или обледенения
параболоидом,
сохранится ли
оптическое
свойство
параболоида
фокусировать
отражённые лучи
в одной точке –
cos
2
фокусе?
1 sin
sin
cos
13. Следствие 6. Параболическая поверхность после обгорания, обледенения или покраски теряет свойства фокусировать отражённые лучи
в одной точке.14. Утверждение 2. Касательная к гиперболе в произвольной точке отсекает от асимптот отрезки, произведение которых постоянно и не
М1y2 x2
2 1
2
b
a
М2
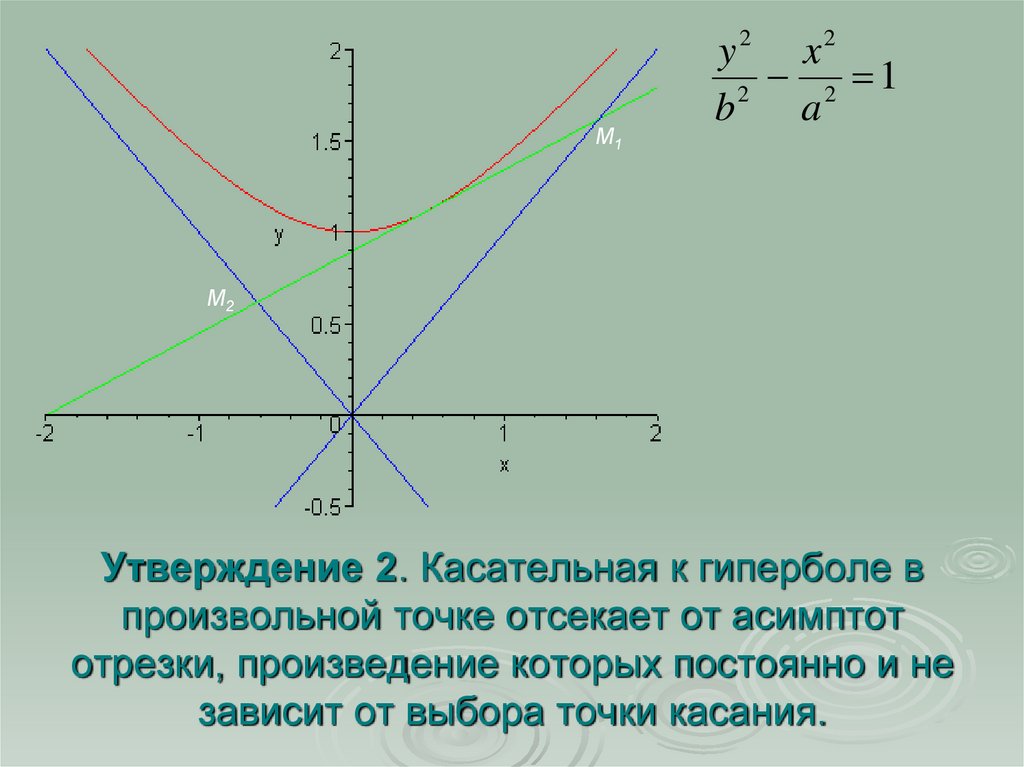
Утверждение 2. Касательная к гиперболе в
произвольной точке отсекает от асимптот
отрезки, произведение которых постоянно и не
зависит от выбора точки касания.
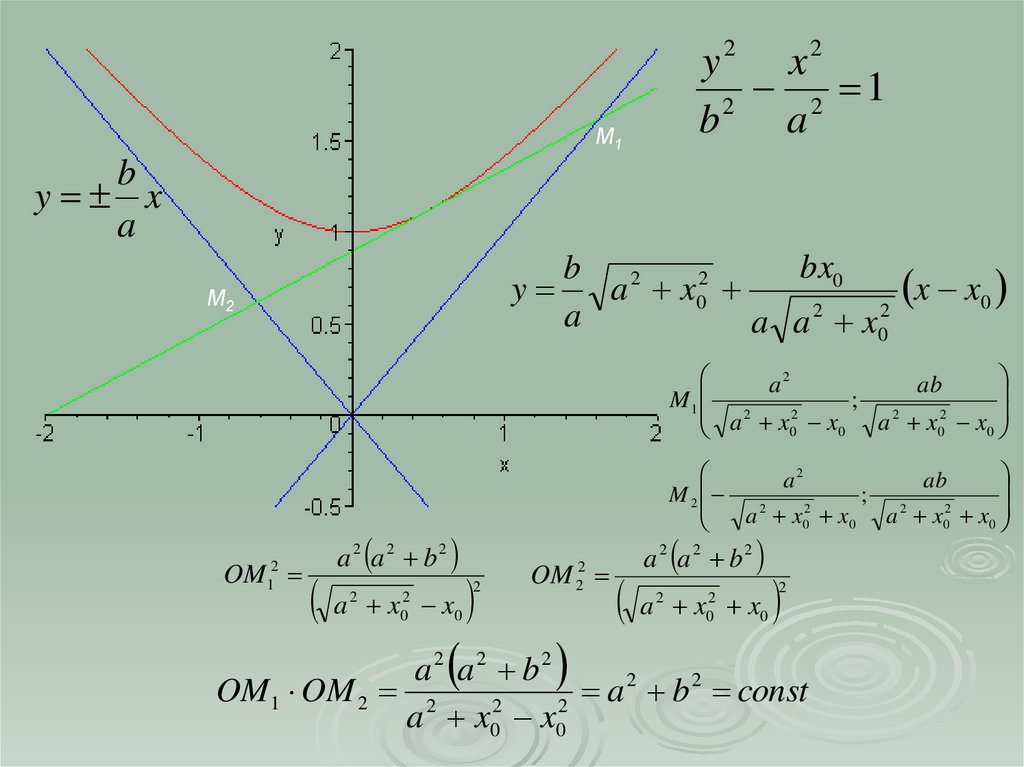
15.
y2 x22 1
2
b
a
М1
b
y x
a
bx0
b 2
2
x x0
y
a x0
2
2
a
a a x0
М2
a2
ab
M1
;
2
2
2
2
a x x
a x0 x0
0
0
OM
2
1
a 2 a 2 b 2
a
2
x x0
2
0
2
a
ab
M2
;
2
2
2
2
a x0 x0 a x0 x0
2
OM
2
2
a 2 a 2 b 2
a
2
x02 x0
2
a 2 a 2 b 2
2
2
OM1 OM 2 2
a
b
const
2
2
a x0 x0
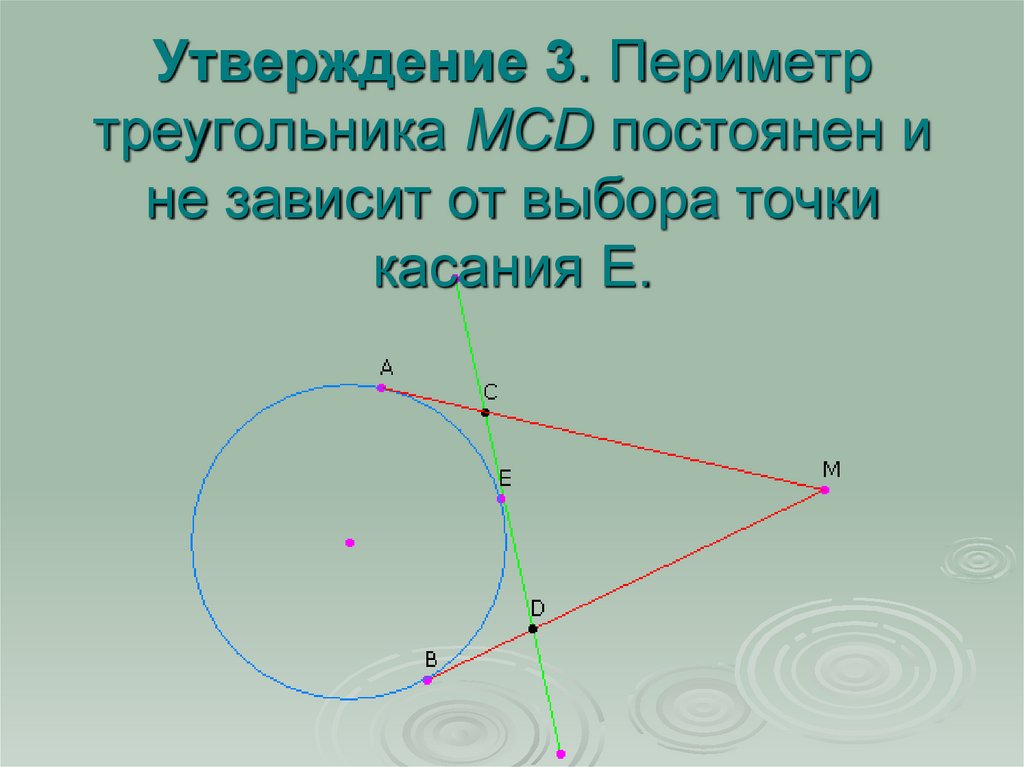
16. Утверждение 3. Периметр треугольника MCD постоянен и не зависит от выбора точки касания Е.
17.
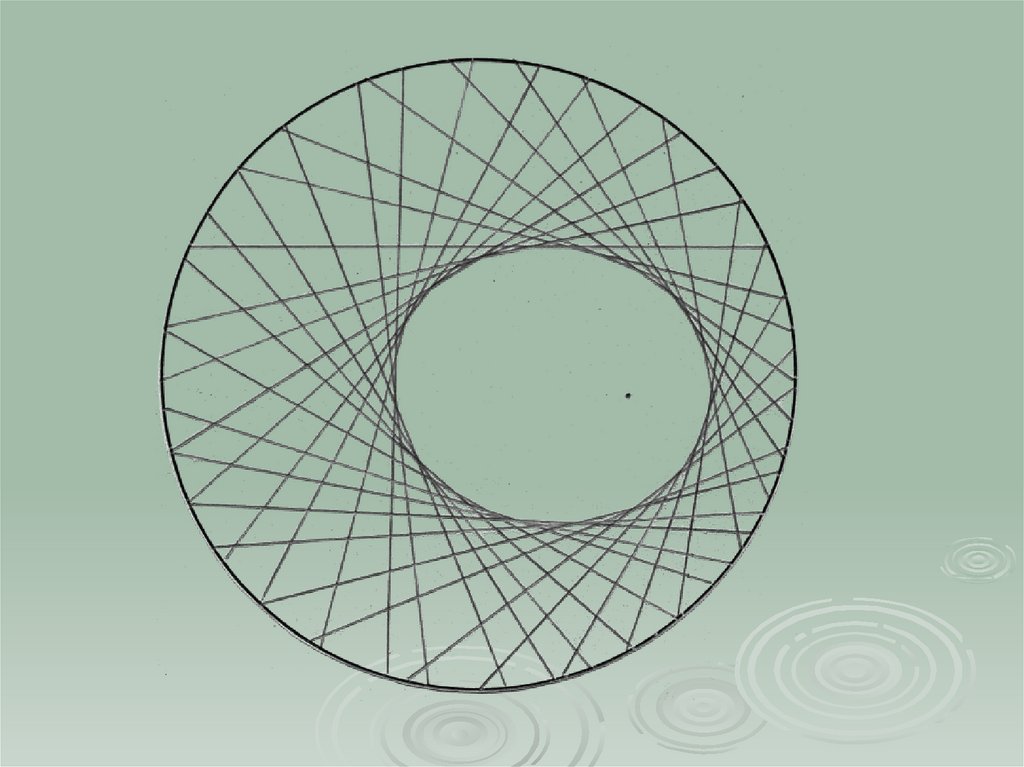
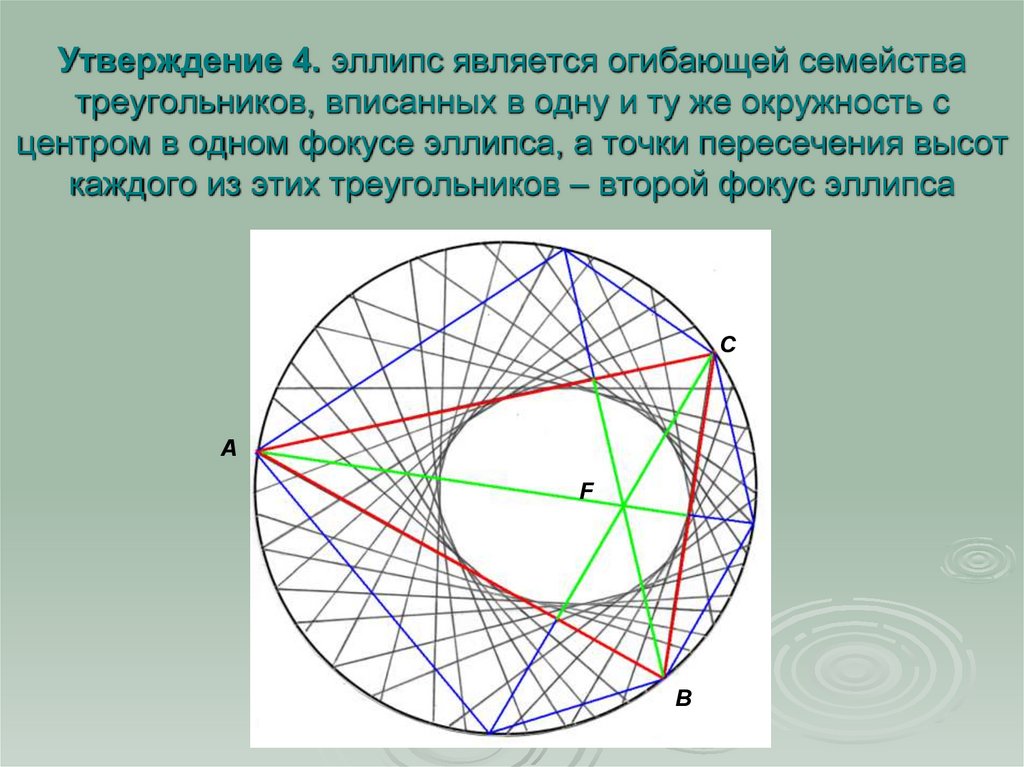
18. Утверждение 4. эллипс является огибающей семейства треугольников, вписанных в одну и ту же окружность с центром в одном фокусе
эллипса, а точки пересечения высоткаждого из этих треугольников – второй фокус эллипса
C
A
F
B
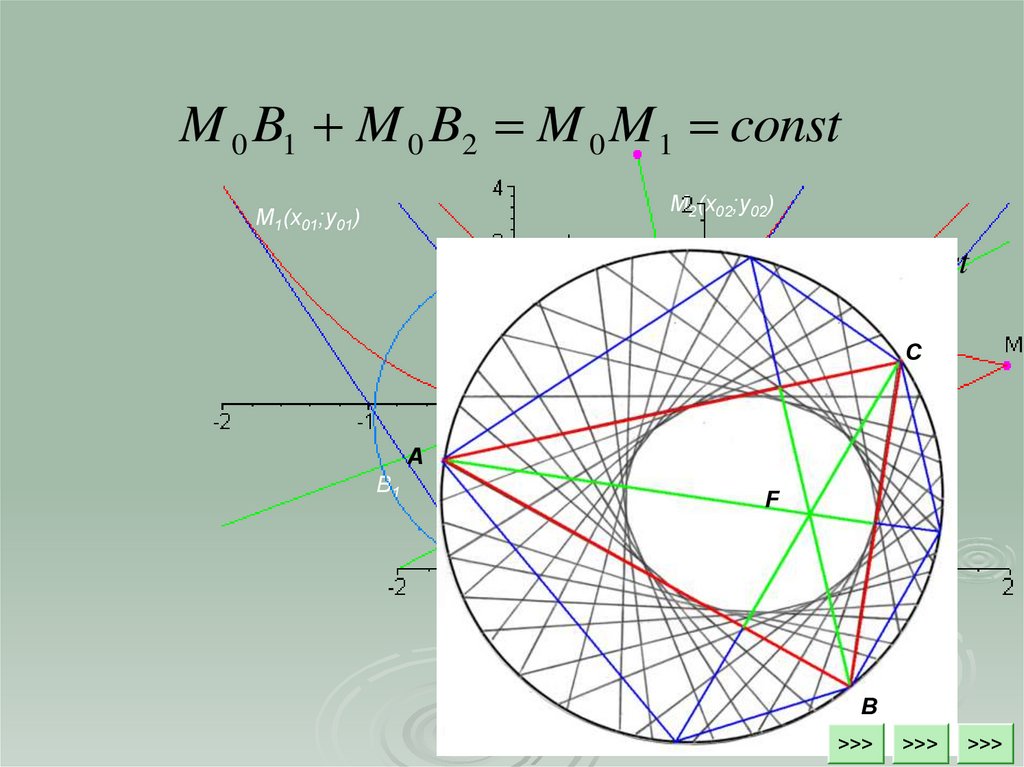
19.
M 0 B1 M 0 B2 M 0 M 1 constМ2(x02;y02)
М1(x01;y01)
P MCD const
P
C
B2
A
B1
F
М0(x0;y0)
B
OM 1 OM 2 const
>>>
>>>
>>>






 Математика
Математика








