Похожие презентации:
Использование координатно-параметрического метода при решении алгебраических задач ЕГЭ типа С5
1. Издательство «Легион»
Использование координатнопараметрического метода прирешении алгебраических
задач ЕГЭ типа С5
докладчик:
Войта Елена
Александровна
2. КП-метод
Пусть на плоскости даны две взаимно перпендикулярныечисловые оси с общим началом в точке О. Ось Ox
называется координатной, а ось Oa – параметрической.
Вся плоскость называется координатно-параметрической
(КП-плоскость).
Метод решения задач с параметрами, использующий КПплоскость называется координатно-параметрическим или
КП-методом.
КП-метод основан на нахождении множества всех точек КПплоскости, значения координаты x и параметра a каждой из
которых удовлетворяют условию задачи.
3.
Издательство «Легион»№1. Найдите все значения параметра а, при каждом из
которых неравенство
x a
0
x 6a
выполняется при всех значениях х, таких, что
2 x 3
Ответ:
1
;
2
2 .
3
4.
Издательство «Легион»Решение
4
5.
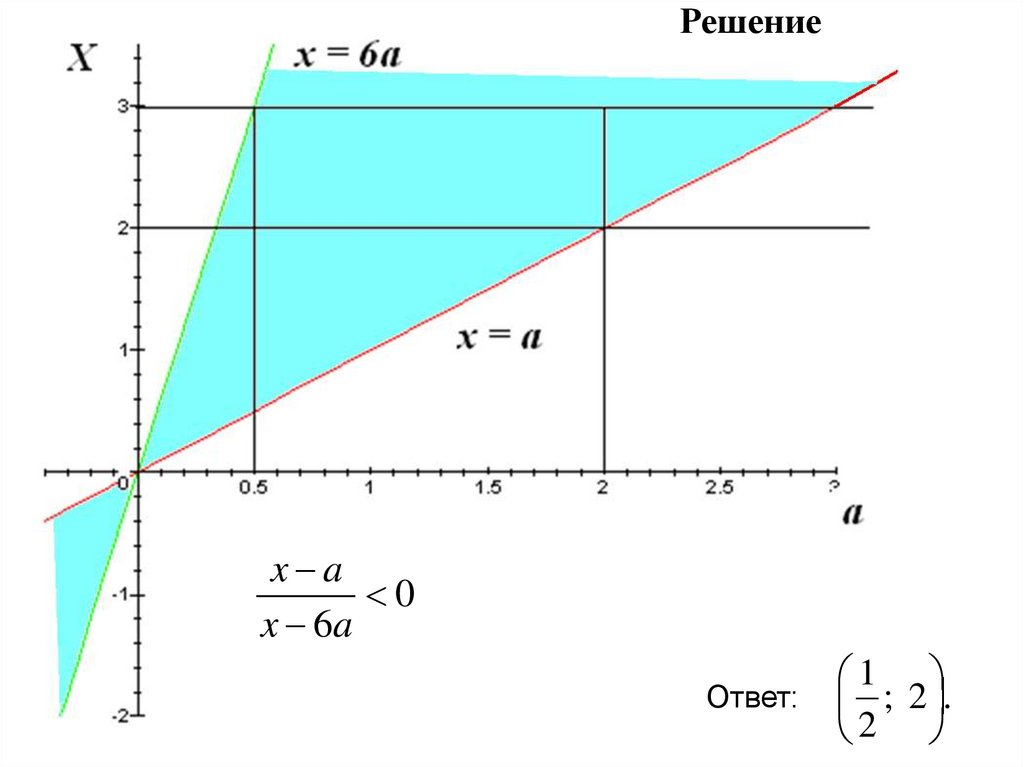
Решениеx a
0
x 6a
Ответ:
1
; 2 .
2
6.
Издательство «Легион»№2. При каких значениях параметра а все корни уравнения
3ax (3a 12a 1) x a(a 4) 0
2
3
2
x 1?
удовлетворяют условию
Ответ: 0 2 3; 2 5 .
6
7.
Издательство «Легион»Решение
7
8.
9.
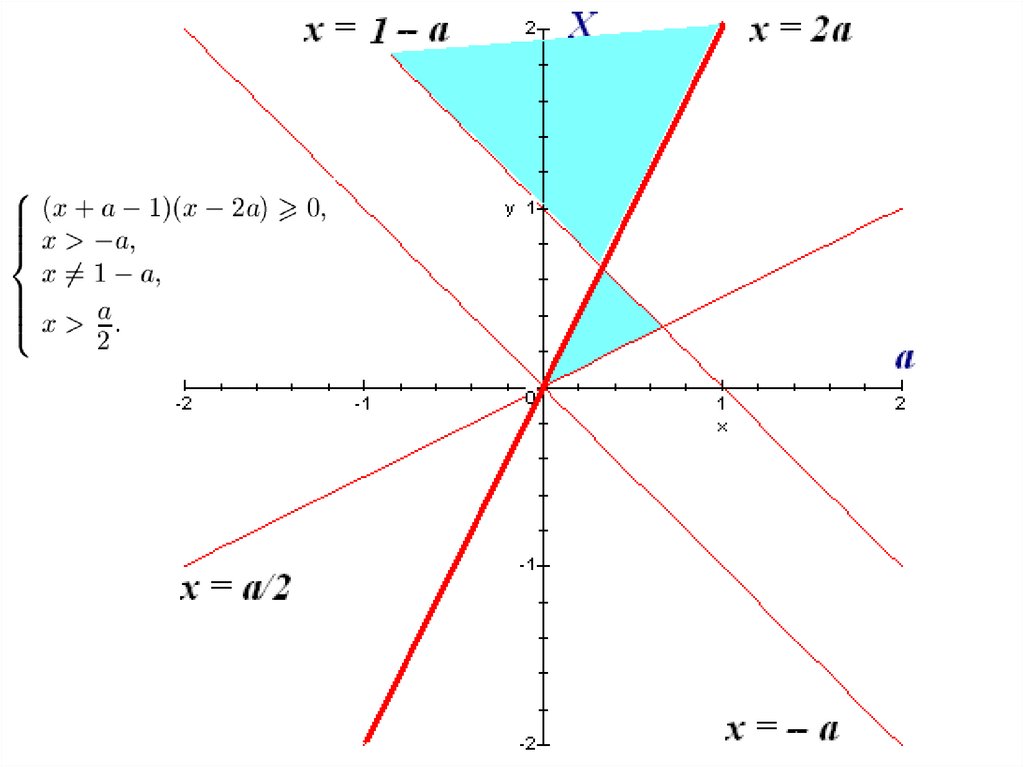
Издательство «Легион»№3. Для каждого значения параметра a решите неравенство
log x a (2 x a) 1.
Ответ:
a 0, x (1 a; ),
1
a
0 a , x ;2a 1 a; ,
3
2
1
1 2 2
a , x ; ; ,
3
6 3 3
1
2
a
a , x ;1 a 2a; ,
3
3
2
2
a , x 2a; .
3
9
10.
Издательство «Легион»Решение
11.
12.
Ответ:a 0, x (1 a; ),
1
a
0 a , x ;2a 1 a; ,
3
2
1
1 2 2
a , x ; ; ,
3
6 3 3
1
2
a
a , x ;1 a 2a; ,
3
3
2
2
a , x 2a; .
3
13.
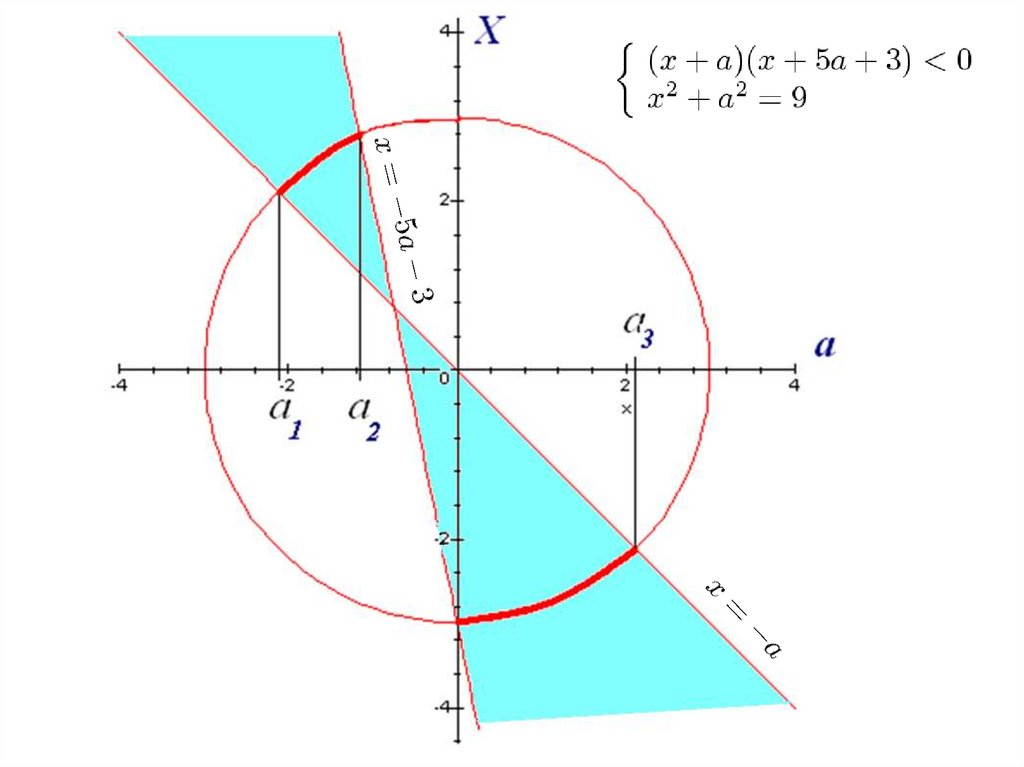
Издательство «Легион»№4. Найдите все значения a, при каждом из которых
система
x (6a 3) x 5a 3a 0,
2
2
x a 9
2
2
имеет решения.
3 2 15 3 2
Ответ:
; 0;
.
13
2
2
13
14.
15.
16.
17. Литература
1. Моденов В. П. Задачи с параметрами. Координатнопараметрический метод: учебное пособие. – М.:«Экзамен», 2007. – 285 с.
2. Горнштейн П. И., Полонский В. Б., Якир М. С. Задачи с
параметрами. – К.: РИА «Текст»; МП «ОКО». 1992. – 290 с.
3. Легион, под.ред. Лысенко, Кулабухова. Задание С5: учимся
решать задачи с параметром.









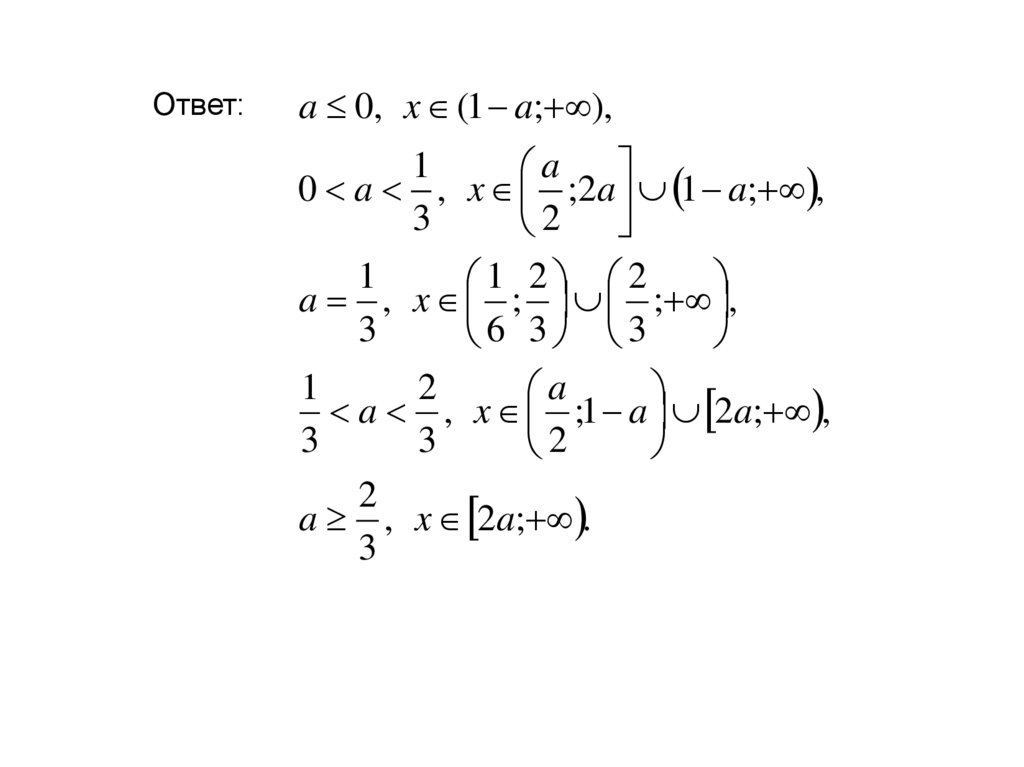



 Математика
Математика Педагогика
Педагогика








