Похожие презентации:
Плоскость
1.
ПлоскостьДисциплина Математика 1
Лекция 5
2016-17 учебный год
2.
План Лекции1. Основные уравнения плоскости
2. Построение плоскости
3. Взаимное расположение
плоскостей
4. Расстояние от точки до плоскости
3. 1. Плоскость
Основные уравнения плоскости1. Уравнение плоскости, проходящей через заданную
точку M 0 ( x0 ; y0 ; z0 ) перпендикулярно
заданному вектору N A; B; C
N A; B; C
A( x x0 ) B( y y0 ) C ( z z0 ) 0
2. Общее уравнение плоскости
M 0 ( x0 ; y0 ; z0 )
Ax By Cz D 0
N A; B; C
Z
- вектор нормали
c
3. Уравнение плоскости « в отрезках»
x y z
1
a b c
Y
a
X
b
4. Уравнения плоскости
4. Уравнение плоскости, проходящей через тризаданные точки M 1 ( x1 ; y1 ; z1 ) , M 2 ( x2 ; y2 ; z2 ) и M 3 ( x3 ; y3 ; z3 )
N A; B; C
M ( x; y; z )
M 2 ( x2 ; y 2 ; z 2 )
M 1 ( x1 ; y1 ; z1 )
M 3 ( x3 ; y3 ; z3 )
Условие компланарности векторов
x x1
y y1
z z1
x2 x1
y2 y1
z 2 z1 0
x3 x1
y3 y1
z3 z1
M 1M x x1 ; y y1 ; z z1
M 1M 2 x2 x1 ; y2 y1 ; z 2 z1
M1M 3 x3 x1; y3 y1 ; z3 z1
( M 1M M 1M 2 M 1M 3 ) 0
5. Построение плоскостей
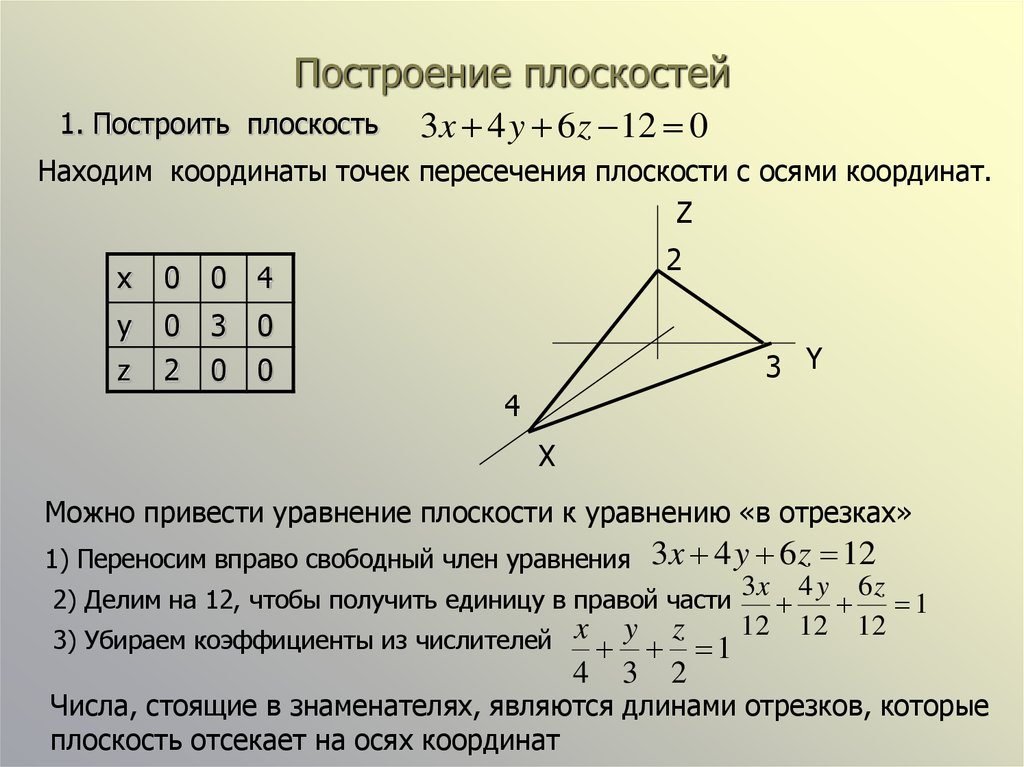
1. Построить плоскость3x 4 y 6 z 12 0
Находим координаты точек пересечения плоскости с осями координат.
Z
x
0
0
4
y
0
3
0
z
2
0
0
2
3 Y
4
X
Можно привести уравнение плоскости к уравнению «в отрезках»
1) Переносим вправо свободный член уравнения
3x 4 y 6 z 12
2) Делим на 12, чтобы получить единицу в правой части
3) Убираем коэффициенты из числителей
x y z
1
4 3 2
3x 4 y 6 z
1
12 12 12
Числа, стоящие в знаменателях, являются длинами отрезков, которые
плоскость отсекает на осях координат
6. Построение плоскостей
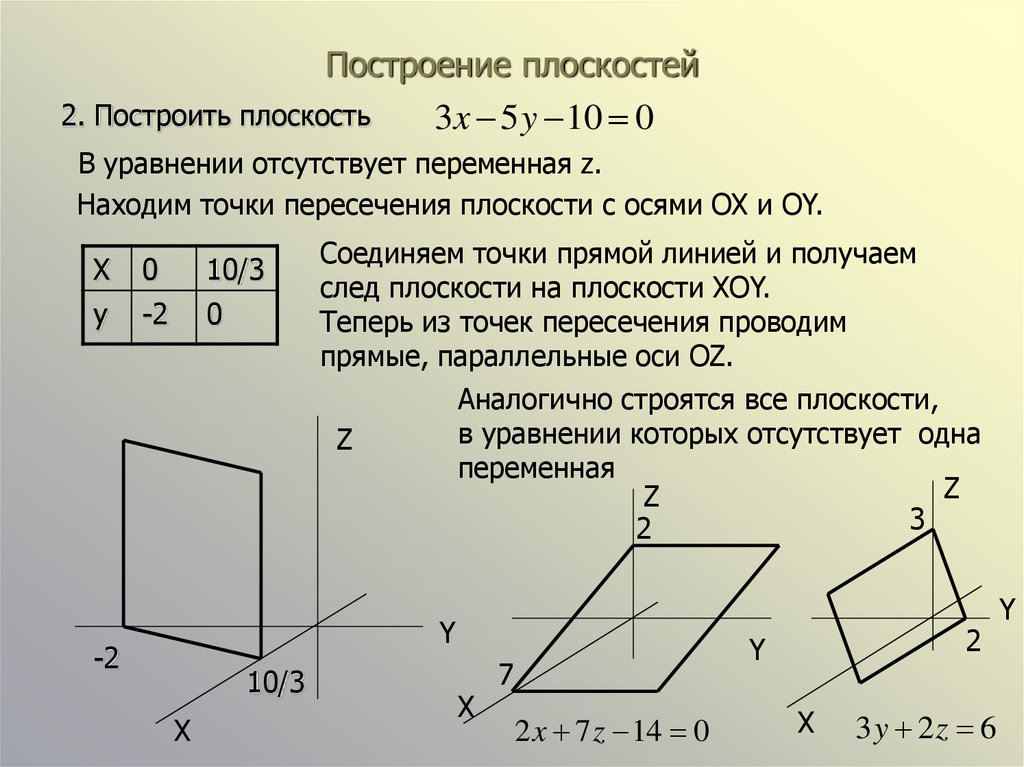
2. Построить плоскость3x 5 y 10 0
В уравнении отсутствует переменная z.
Находим точки пересечения плоскости с осями OX и OY.
X
0
10/3
y
-2
0
Соединяем точки прямой линией и получаем
след плоскости на плоскости XOY.
Теперь из точек пересечения проводим
прямые, параллельные оси OZ.
Аналогично строятся все плоскости,
в уравнении которых отсутствует одна
переменная
Z
Z
3
2
Z
Y
-2
10/3
X
X
2
Y
7
2 x 7 z 14 0
X
3 y 2z 6
Y
7. Построение плоскостей
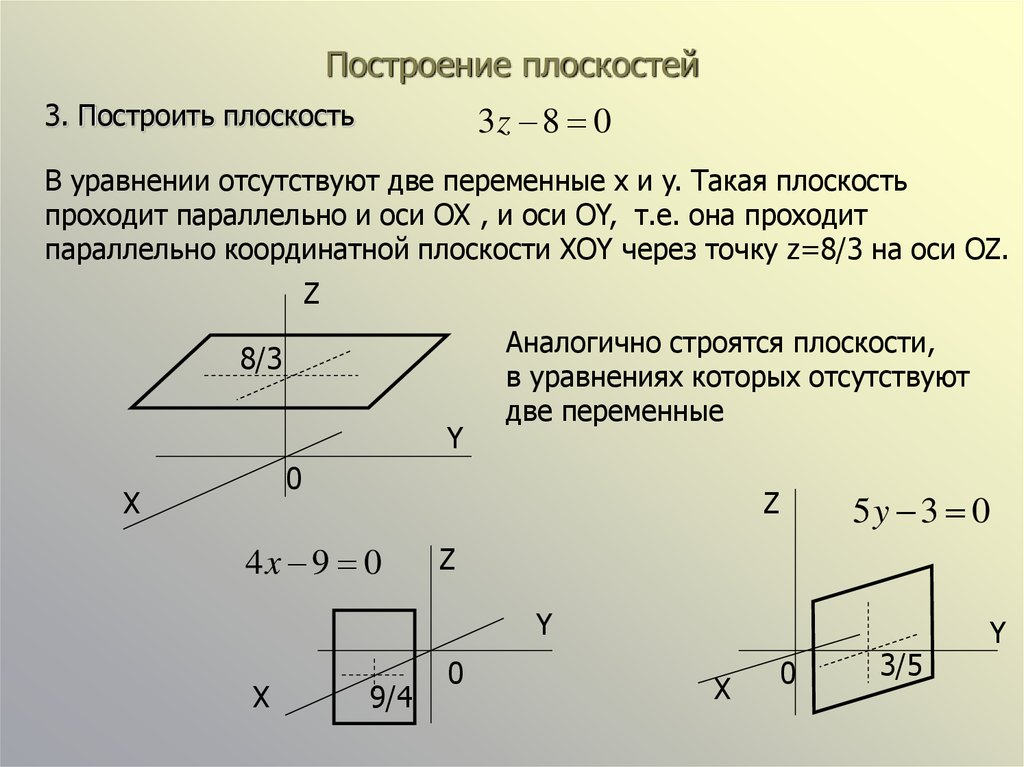
3z 8 03. Построить плоскость
В уравнении отсутствуют две переменные x и y. Такая плоскость
проходит параллельно и оси OX , и оси OY, т.е. она проходит
параллельно координатной плоскости XOY через точку z=8/3 на оси OZ.
Z
8/3
Y
Аналогично строятся плоскости,
в уравнениях которых отсутствуют
две переменные
0
X
Z
4x 9 0
5y 3 0
Z
Y
X
9/4
0
X
0
3/5
Y
8.
Таким образом, если в уравнении плоскостиотсутствует одна переменная, то плоскость проходит
параллельно той оси координат, переменной которой
нет в уравнении.
Если в уравнении плоскости отсутствует свободный
член, то плоскость проходит через начало координат.
Если в уравнении плоскости отсутствуют две
переменные, то плоскость проходит параллельно
координатной плоскости, переменных которой нет в
уравнении.
Уравнения координатных плоскостей
- уравнение плоскости YOZ
x 0
- уравнение плоскости XOZ
y 0
- уравнение плоскости XOY
z 0
9. Взаимное расположение плоскостей
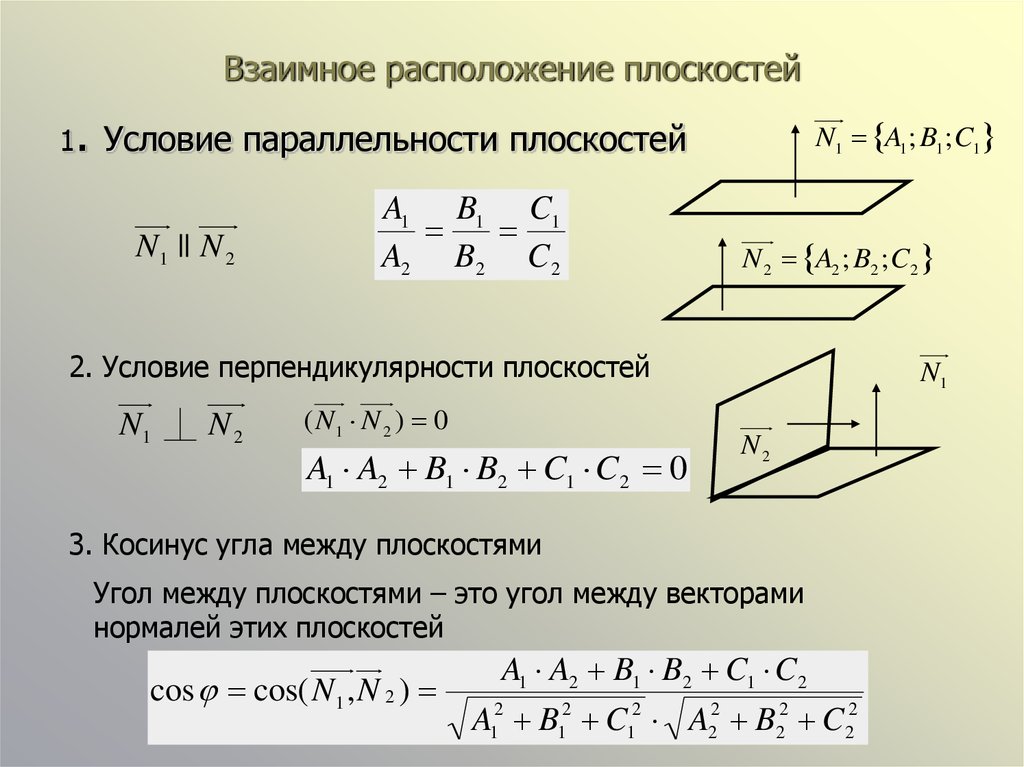
1. Условие параллельности плоскостейN 1 || N 2
A1 B1 C1
A2 B2 C 2
N1 A1 ; B1 ; C1
N 2 A2 ; B2 ; C2
2. Условие перпендикулярности плоскостей
N1
N2
( N1 N 2 ) 0
A1 A2 B1 B2 C1 C 2 0
N1
N2
3. Косинус угла между плоскостями
Угол между плоскостями – это угол между векторами
нормалей этих плоскостей
cos cos( N1 , N 2 )
A1 A2 B1 B2 C1 C 2
A12 B12 C12 A22 B22 C 22
10. Расстояние от точки до плоскости
Расстояние от точки M 1 ( x1 ; y1 ; z1 ) до плоскостиAx By Cz D 0 находится по формуле
d
| Ax1 By1 Cz1 D |
M 1 ( x1 ; y1 ; z1 )
d
A2 B 2 C 2
Расстояние – это длина перпендикуляра, опущенного из точки на плоскость
Правило: для нахождения расстояния от точки до плоскости нужно
координаты точки подставить в левую часть уравнения плоскости,
разделить на длину вектора нормали плоскости и полученное значение
взять по абсолютной величине.
!
Расстояние – величина всегда положительная
11.
Задание на СРС1. Построение произвольных плоскостей. [1]
2. Точка пересечения трех плоскостей (конспект).
Задание на СРСП
1. ИДЗ – 3.1. [1. стр.97].
Глоссарий
№
1
2
3
4
5
На русском языке
Плоскость
Общее уравнение
Параметрическое
Каноническое
Нормаль
На казахском языке
Жазықтық
Жалпы теңдеу
Параметрлік
Канондық
Нормаль
На английском языке
Plane
General equation
Parameter
Canon
Normal vector
Литература:
Основная
А.П. Рябушко. Индивидуальные задания по высшей математике, т.1.- Мн.: Выш. Школа, 2011.
Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах: Учебное пособие для втузов.
- М.: Оникс, 2007.
Дополнительная
Буганова С.Н. Математика для технических специальностей с применением прикладных программ.
- Алматы: КазГАСА, 2015, с.108.
Сыдыкова Д.К. «Курс Математики- I», Модуль I, II для дистанционного обучения. Электронный
учебник.-Алматы: КазГАСА, 2012.
www.studentlibrary.ru
http://sferaznaniy.ru/vysshaya-matematika.







 Математика
Математика








