Аналитическая геометрия. Уравнение поверхности и уравнения линии в пространстве. Плоскость

1.

2.

3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
3.1 Линии на плоскости и их уравнения
3.2 Прямая линия на плоскости
3.3 Кривые второго порядка
3.4 Уравнение поверхности и уравнения линии в
пространстве
3.5 Плоскость
3.6 Прямая линия в пространстве
3.7 Взаимное расположение прямой и плоскости

3.

3.4 УРАВНЕНИЕ ПОВЕРХНОСТИ И УРАВНЕНИЯ ЛИНИИ В ПРОСТРАНСТВЕ
Уравнение вида F x; y; z 0 называется уравнением поверхности
в декартовой системе координат Oxyz, если:
1) координаты х, у, z любой точки М(х;у;z) удовлетворяют этому
уравнению,
2) координаты х, у, z любой точки N(х;у;z) не удовлетворяют ему.
М(х;у;z) - текущая точка поверхности
х, у, z - текущие координаты
Если две поверхности пересекаются, то они образуют некоторую линию
в пространстве.
Линия L в пространстве задаётся системой уравнений, которые являются
уравнениями двух поверхностей (координаты точки М(х;у;z) L
удовлетворяют одновременно этим двум уравнениям):
F1 x; y; z 0,
L:
F2 x; y; z 0

4.

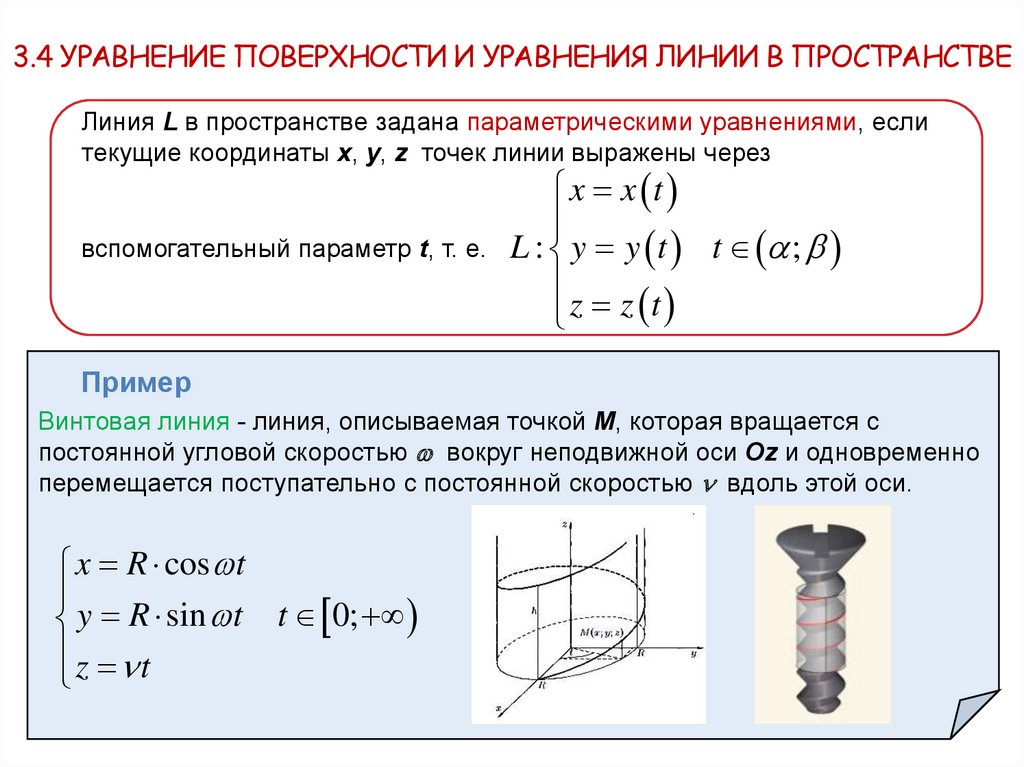
3.4 УРАВНЕНИЕ ПОВЕРХНОСТИ И УРАВНЕНИЯ ЛИНИИ В ПРОСТРАНСТВЕ
Линия L в пространстве задана параметрическими уравнениями, если
текущие координаты х, у, z точек линии выражены через
вспомогательный параметр t, т. е.
x x t
L : y y t t ;
z z t
Пример
Винтовая линия - линия, описываемая точкой M, которая вращается с
постоянной угловой скоростью вокруг неподвижной оси Oz и одновременно
перемещается поступательно с постоянной скоростью вдоль этой оси.
x R cos t
y R sin t t 0;
z t

5.

3.5 ПЛОСКОСТЬ
Задача 1
n
M0
z
x
O
Вывести уравнение плоскости P, проходящей через
заданную точку, перпендикулярно заданному вектору.
M
P
y
Дано:
M 0 x0 ; y0 ; z0 P, n A; B; C P
Найти: P
Решение:
M x; y; z P – текущая точка, тогда M 0 M x x0 ; y y0 ; z z0
n M 0 M критерий перпендикулярности векторов n M 0 M 0
A x x0 B y y0 C z z0 0
Ax Ax0 By By0 Cz Cz0 0
Ax By Cz Ax0 By0 Cz0 0
Пусть
общее уравнение плоскости
D
Ax By Cz D 0
n A; B; C – нормальный вектор

6.

3.5 ПЛОСКОСТЬ
Замечание
Ax By Cz D 0
A 0 By Cz D 0
Плоскость параллельна оси Oх
B 0 Ax Cz D 0
Плоскость параллельна оси Оу
C 0 Ax By D 0
Плоскость параллельна оси Оz
2
D 0 Ax By Cz 0
Плоскость проходит через
начало координат
3
A D 0 By Cz 0
Плоскость проходит через ось Oх
B D 0 Ax Cz 0
Плоскость проходит через ось Оу
C D 0 Ax By 0
Плоскость проходит через ось Оz
1
4
A B 0 Cz D 0
Плоскость параллельна плоскости Oху
B C 0 Ax D 0
Плоскость параллельна плоскости Оуz
A C 0 By D 0
Плоскость параллельна плоскости Охz

7.

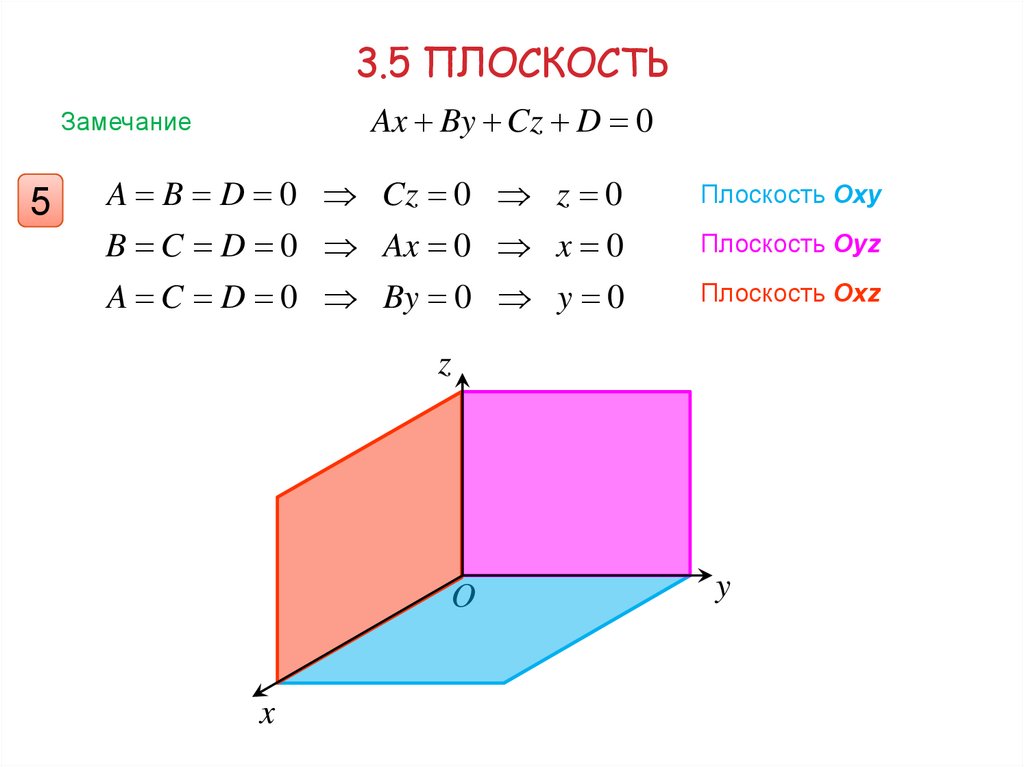
3.5 ПЛОСКОСТЬ
Ax By Cz D 0
Замечание
5
A B D 0 Cz 0 z 0
Плоскость Oху
B C D 0 Ax 0 x 0
Плоскость Оуz
A C D 0 By 0 y 0
Плоскость Охz
z
O
x
y

8.

3.5 ПЛОСКОСТЬ
Задача 2
M1
Вывести уравнение плоскости P, проходящей
через три заданные точки.
M
M2
M3
z
Дано: M 1 x1; y1; z1 , M 2 x2 ; y2 ; z2 , M 3 x3 ; y3 ; z3 P
P
Найти: P
x
O
y
Решение:
M 1M 2 x2 x1; y2 y1; z2 z1 , M 1M 3 x3 x1; y3 y1; z3 z1
Пусть
M x; y; z P – текущая точка, тогда M 1M x x1; y y1; z z1
M 1 M , M 1M 2 , M 1M 3
компланарные
x x1
y y1
z z1
x2 x1
y2 y1
z2 z1 0
x3 x1
y3 y1
z3 z1
M M , M M , M M 0
1
1
2
1
3
уравнение плоскости,
проходящей через три
заданные точки

9.

3.5 ПЛОСКОСТЬ
z
Замечание
C
x x1
y y1
z z1
x2 x1
y2 y1
z2 z1 0
x3 x1
y3 y1
z3 z1
c
P
a
y
O
x
B
b
A
Пусть заданные точки расположены на осях координат, т. е. отсекают на
осях заданные отрезки,
Тогда координаты этих точек: A a;0;0 , B 0; b;0 , C 0;0; c .
x a
y 0 z 0
0 a
b 0 0 0 0
0 a
0 0 c 0
x a
y
z
a
b 0 0
a
0 c

10.

3.5 ПЛОСКОСТЬ
Замечание
x a
y
z
a
b 0 0
a
0 c
Воспользуемся правилом треугольников для
вычисления определителей третьего порядка:
x a bc 0 0 zab yac 0 0
xbc abc zab yac 0
xbc yac zab abc
xbc yac zab abc
abc abc abc abc
x y z
1
a b c
Разделим обе части уравнения на
abc :
уравнение плоскости в отрезках
Это уравнение позволяет быстро сделать чертёж плоскости в декартовой
системе координат.

11.

3.5 ПЛОСКОСТЬ
Пример
Составить общее уравнение плоскости, проходящей через точки
K 2;1;1 , L 4;2;1 , M 2;3; 1 .
Преобразовать это уравнение в уравнение плоскости в отрезках
и сделать чертёж плоскости в декартовой системе координат.
x x1
y y1
z z1
x2 x1
y2 y1
z2 z1 0
x3 x1
y3 y1
z3 z1
x 2
y 1
z 1
4 2
2 1
1 1 0
2 2 3 1 1 1
y 1 z 1
2
1
0 0
4
2
2
x 2
x 2
1
0
2 2
y 1
2
0
4 2
z 1
2
1
4 2
0

12.

3.5 ПЛОСКОСТЬ
Пример (продолжение)
x 2 2 y 1 4 z 1 8 0
2 x 4 4 y 4 8 z 8 0
2 x 4 y 8 z 8 0
разделим обе части уравнения на (-2):
x 2 y 4z 4 0
– общее уравнение плоскости
Преобразуем это уравнение в уравнение плоскости в отрезках:
x 2 y 4 z 4
x 2 y 4 z 4
4 4
4 4
x y z
1
4 2 1
разделим обе части уравнения на (-4):
– уравнение плоскости в отрезках

13.

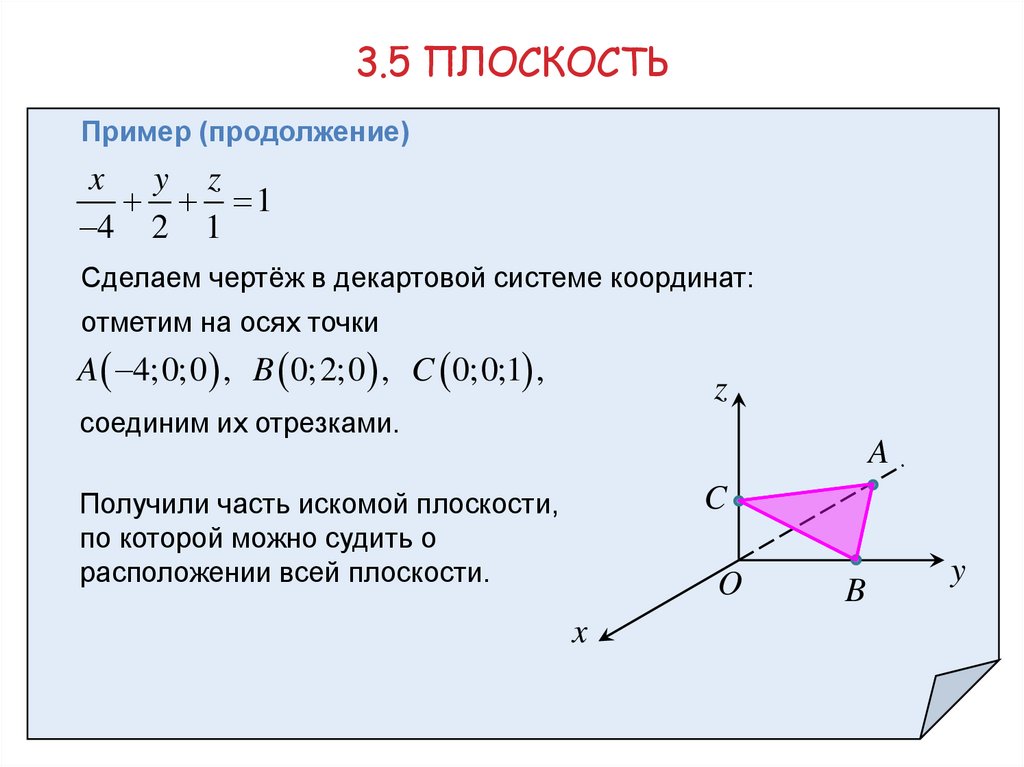
3.5 ПЛОСКОСТЬ
Пример (продолжение)
x y z
1
4 2 1
Сделаем чертёж в декартовой системе координат:
отметим на осях точки
A 4;0;0 , B 0;2;0 , C 0;0;1 ,
z
соединим их отрезками.
A
C
Получили часть искомой плоскости,
по которой можно судить о
расположении всей плоскости.
O
x
B
y

14.

3.5 ПЛОСКОСТЬ
Обобщение
Мы получили несколько типов (форм записи) уравнений плоскости в
пространстве, которые отличаются по внешнему виду:
1) общее уравнение,
2) уравнение плоскости, проходящей через три точки,
3) уравнение плоскости в отрезках.
Очевидно, что с помощью алгебраических преобразований можно легко
перейти от одной формы записи к другой.
Таким образом можно утверждать, что любой способ определения
плоскости в пространстве приводит к уравнению первой степени
относительно х, у, z .
Ax By Cz D 0
( числа А, В и С одновременно не могут быть равны нулю)

15.

3.5 ПЛОСКОСТЬ
Указания к составлению уравнений плоскости
Дано
Выбор формулы
Точка и перпендикулярный
вектор
A x x0 B y y0 C z z0 0
Три точки
x x1
y y1
z z1
x2 x1
y2 y1
z2 z1 0
x3 x1
y3 y1
z3 z1

16.

3.5 ПЛОСКОСТЬ
Взаимное расположение плоскостей
Рассмотрим две плоскости, заданные общими уравнениями,
и соответствующие им нормальные векторы:
P1 : A1 x B1 y C1 z D1 0
P2 : A2 x B2 y C2 z D2 0
1
n1 A1; B1; C1 P1
n2 A2 ; B2 ; C2 P2
Параллельность плоскостей
A1 B1 C1
A2 B2 C2
2
Совпадение плоскостей
A1 B1 C1 D1
A2 B2 C2 D2
3
Перпендикулярность плоскостей
P1 P2 n1 n2 n1 n2 0 A1 A2 B1B2 C1C2 0

17.

3.5 ПЛОСКОСТЬ
Взаимное расположение плоскостей
4
Угол между плоскостями
cos P1; P2 cos n1; n2
L1; L2 arccos
5
n1 n2
n1 n2
A1 A2 B1B2 C1C2
A12 B12 C12 A22 B22 C22
A1 A2 B1B2 C1C2
A B C A B C
2
1
Пересечение плоскостей
A1 x B1 y C1 z D1 0
A2 x B2 y C2 z D2 0
Линией пересечения двух
плоскостей является прямая.
2
1
2
1
2
2
2
2
2
2
L

18.

Лекция выложена впервые.
Если Вы заметили ошибку, то сообщите мне на эл. почту.