Прямоугольный параллелепипед

1. Прямоугольный параллелепипед

Урок 1
Автор: Сидорова А.В.
Учитель математики
МБОУ СОШ № 31
Г. Мурманска

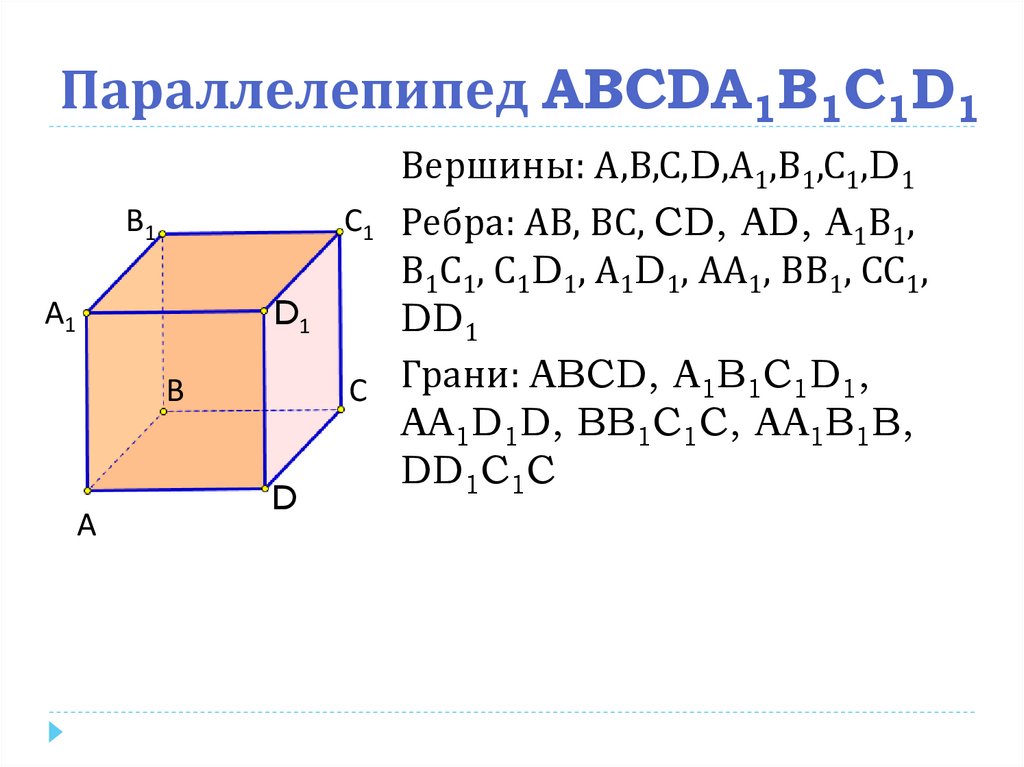
2. Параллелепипед ABCDA1B1C1D1

В1
D1
А1
В
А
D
Вершины: А,В,С,D,А1,В1,С1,D1
С1 Ребра: АВ, ВС, CD, AD, A1В1,
В1С1, С1D1, А1D1, АА1, ВВ1, СС1,
DD1
С Грани: ABCD, A1B1C1D1,
AA1D1D, BB1C1C, AA1B1B,
DD1C1C

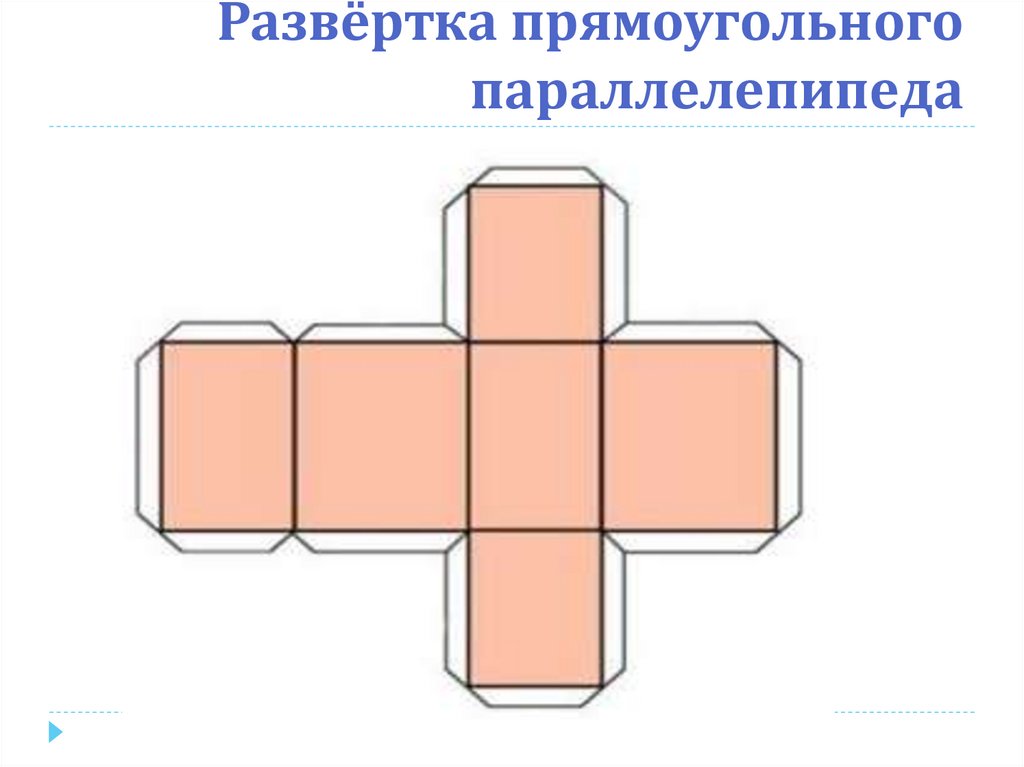
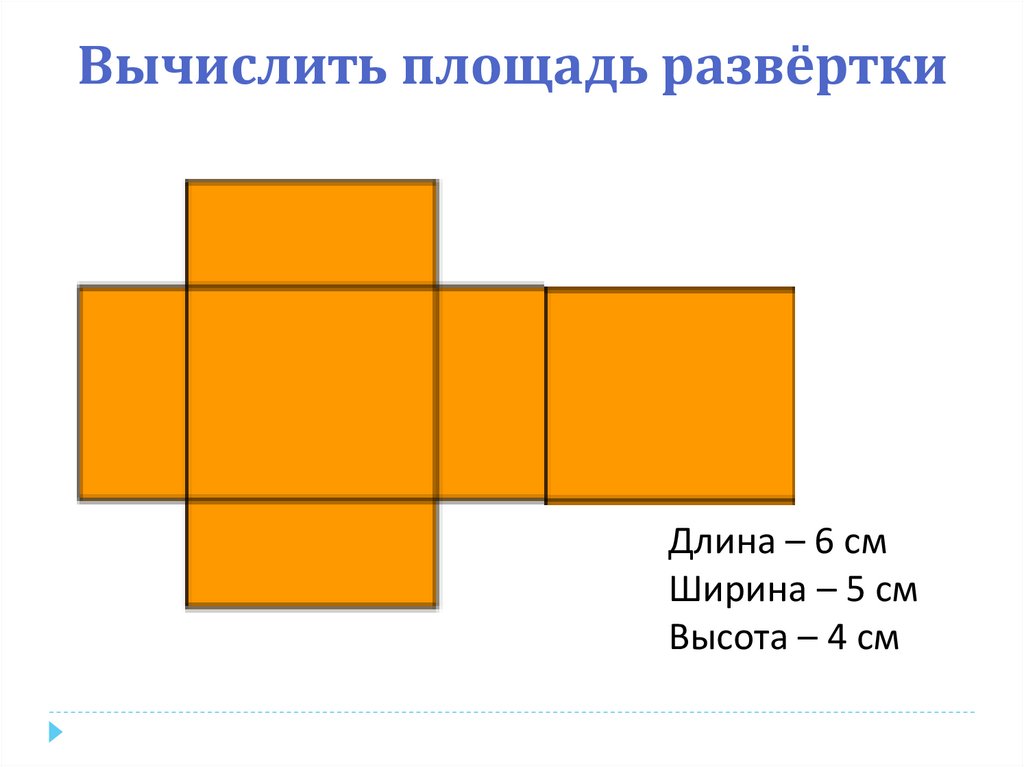
3. Развёртка прямоугольного параллелепипеда

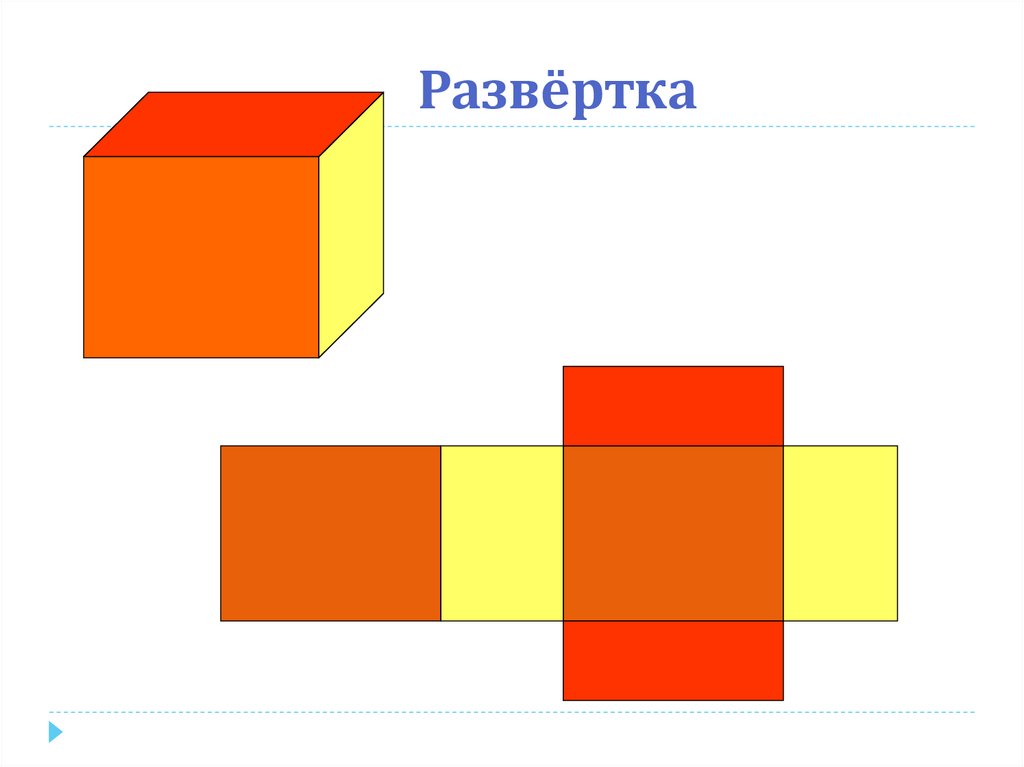
4. Развёртка

5.

1
3
2
4

6.

Вычислить площадь развёртки
Длина – 6 см
Ширина – 5 см
Высота – 4 см

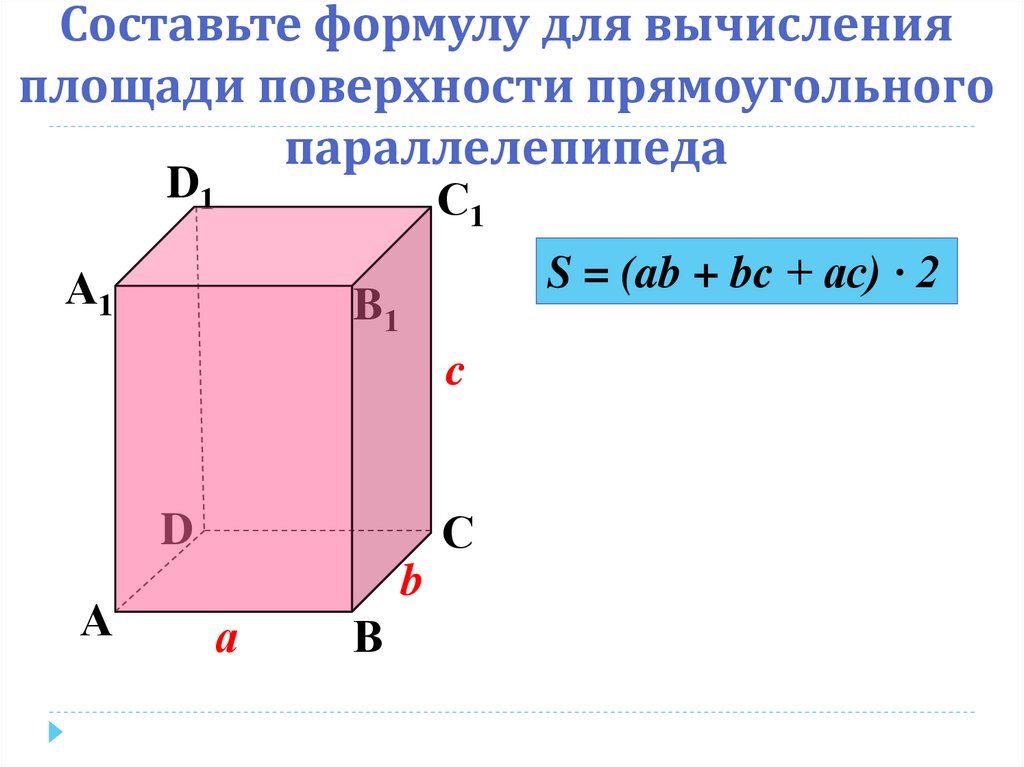
7. Составьте формулу для вычисления площади поверхности прямоугольного параллелепипеда

D1
С1
А1
S = (ab + bc + ac) ∙ 2
B1
c
С
D
А
b
а
В

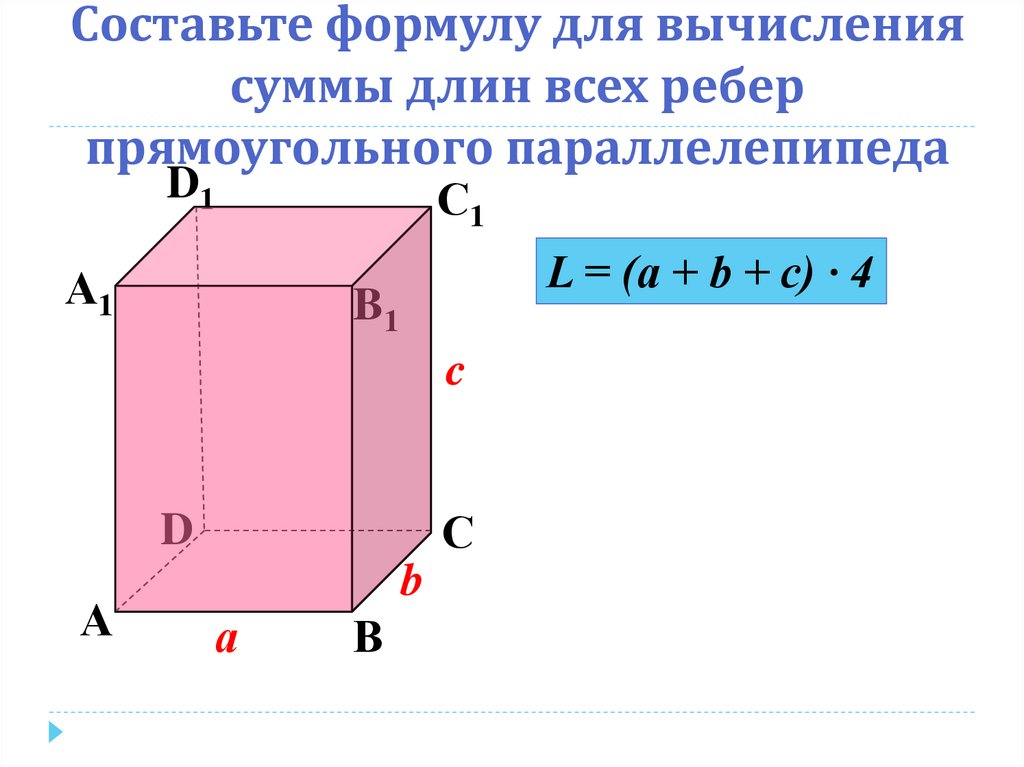
8. Составьте формулу для вычисления суммы длин всех ребер прямоугольного параллелепипеда

D1
С1
А1
L = (a + b + c) ∙ 4
B1
c
С
D
А
b
а
В

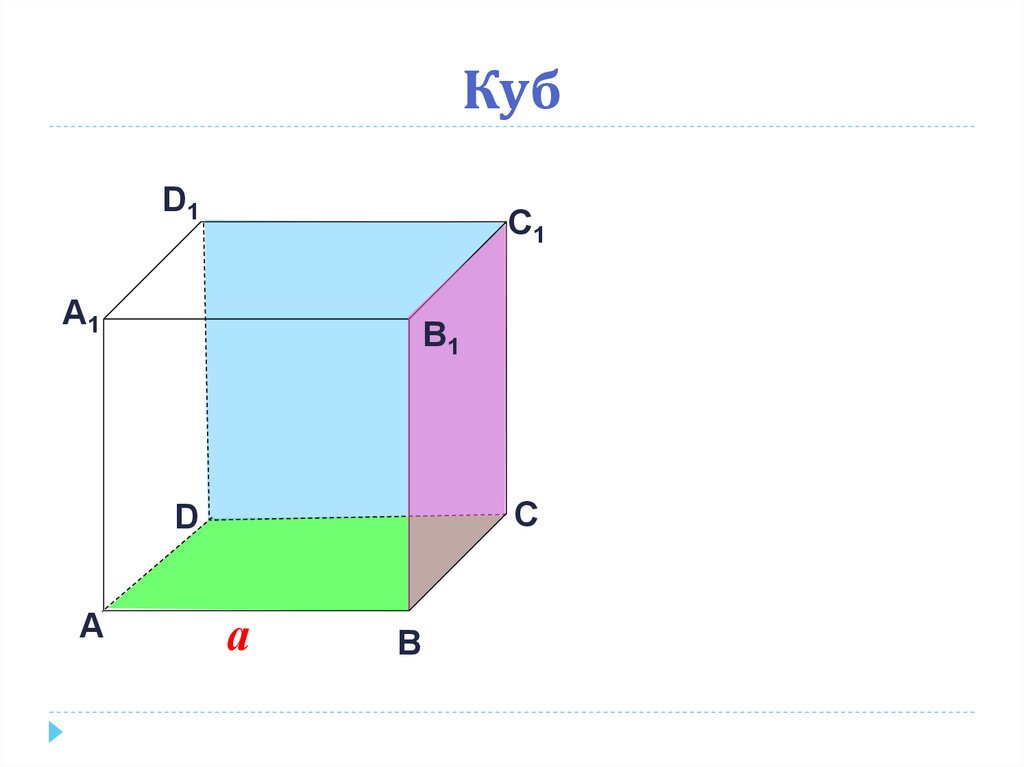
9. Куб

D1
С1
А1
В1
С
D
А
а
В

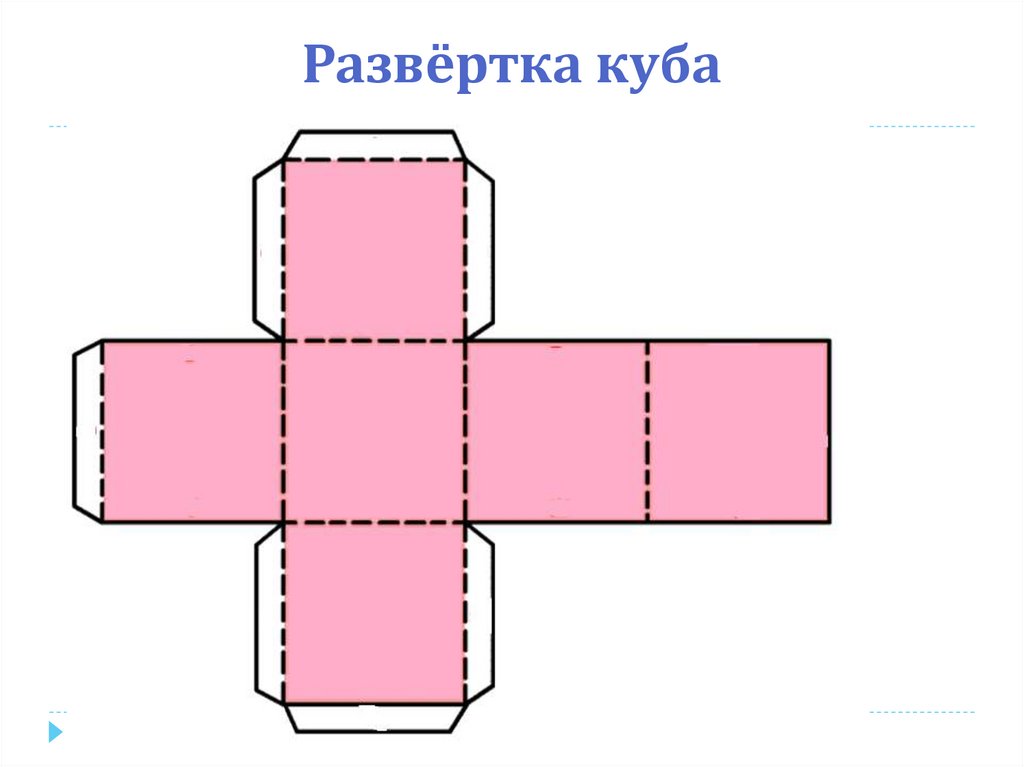
10. Развёртка куба

11.

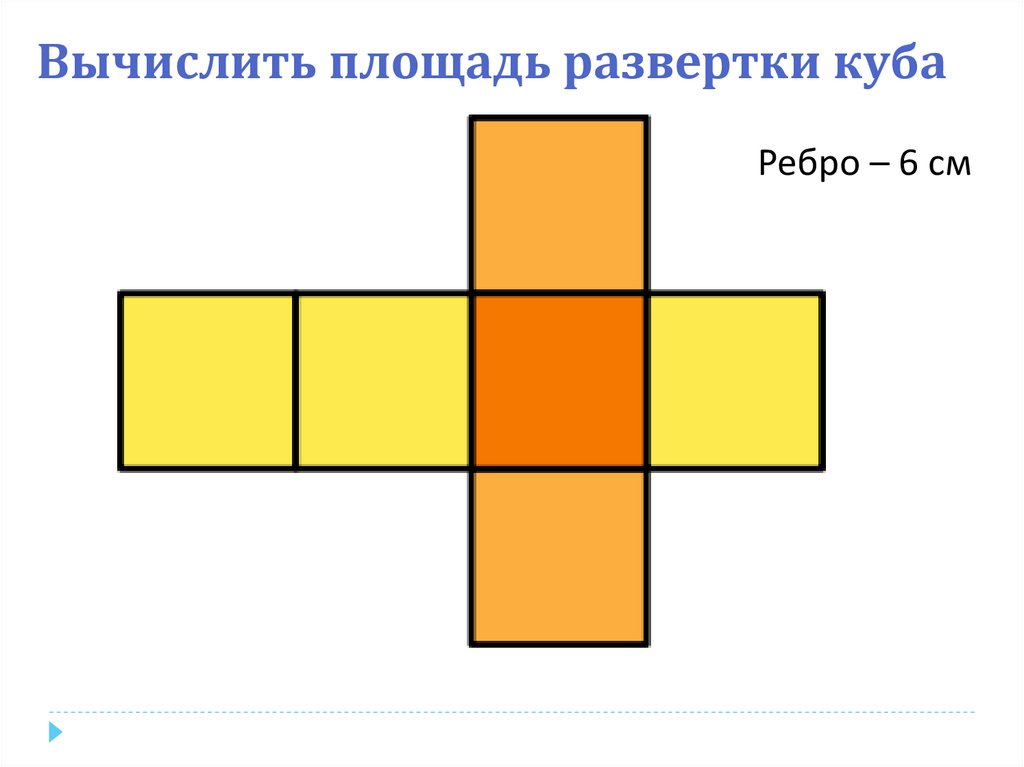
Вычислить площадь развертки куба
Ребро – 6 см

12.

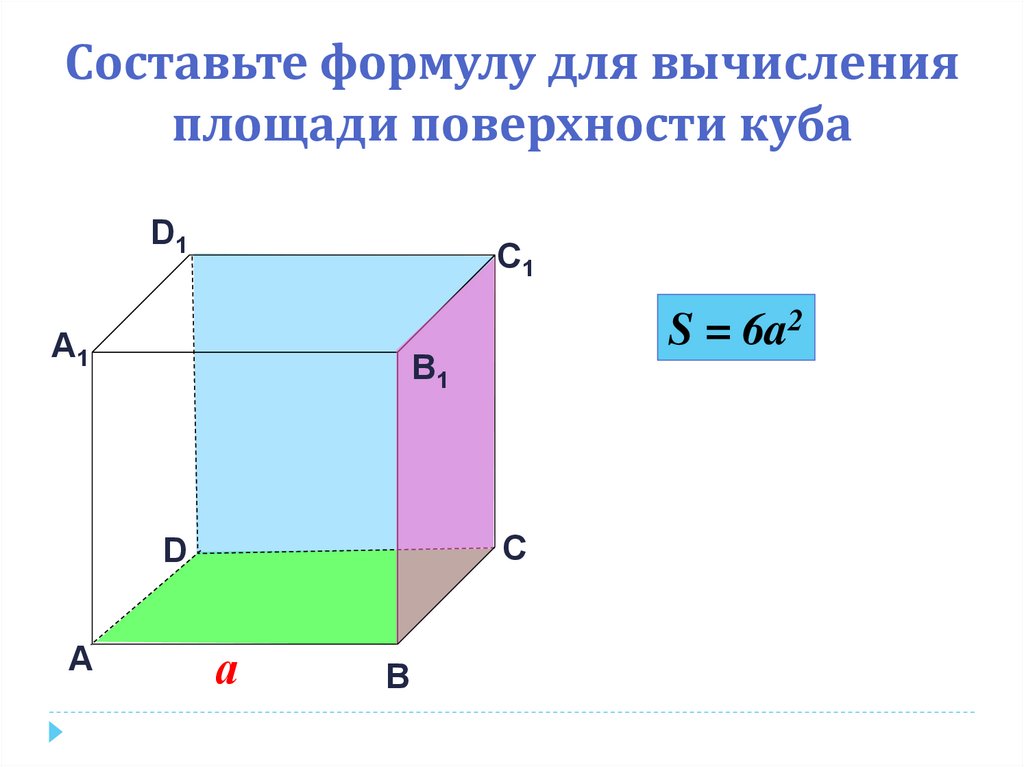
Составьте формулу для вычисления
площади поверхности куба
D1
С1
А1
В1
С
D
А
S = 6a2
а
В

13.

Составьте формулу для вычисления
длин всех ребер куба
D1
С1
А1
В1
С
D
А
L = 12a
а
В

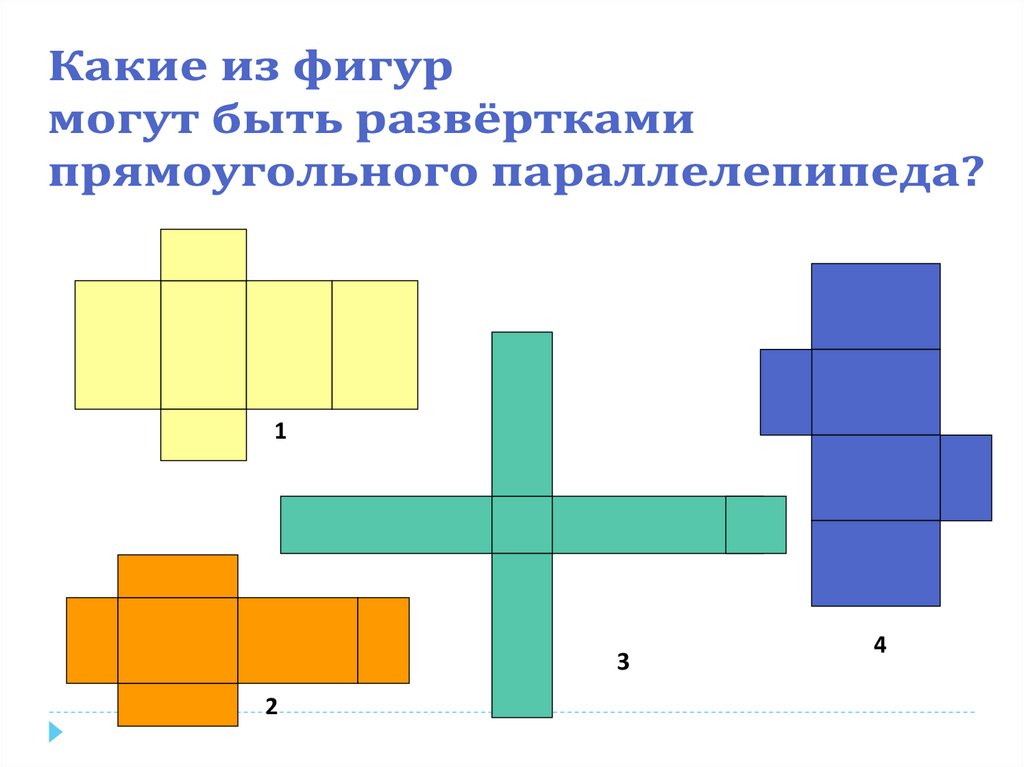
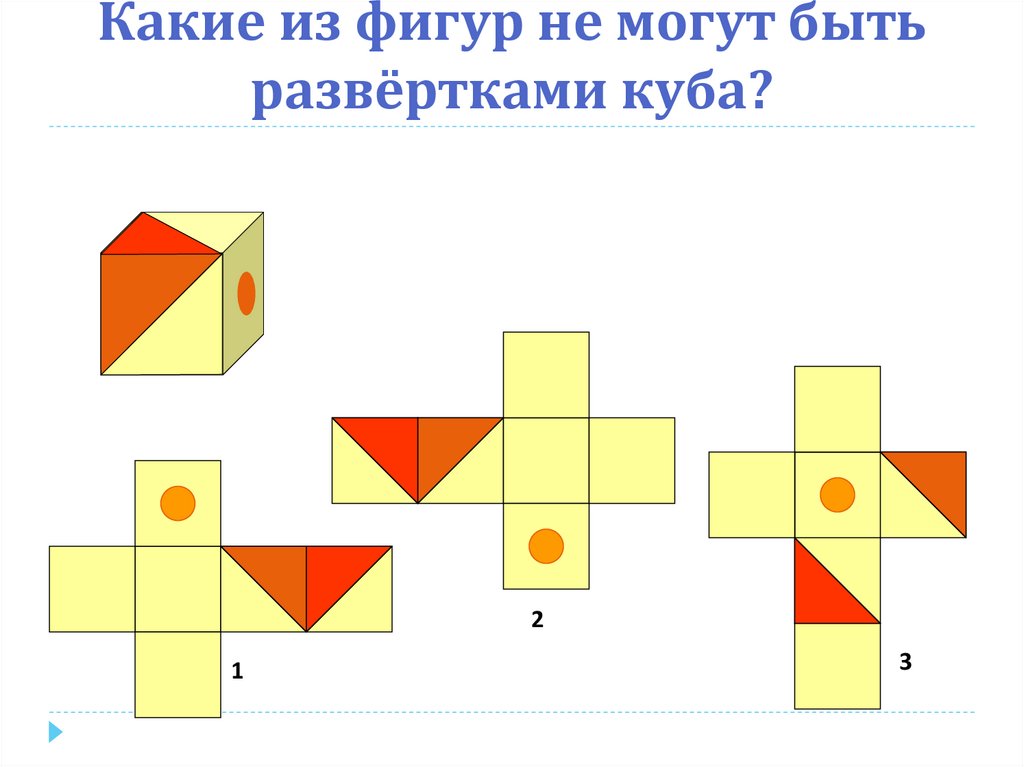
14. Какие из фигур не могут быть развёртками куба?

2
1
3

15. Многогранники и их развертки

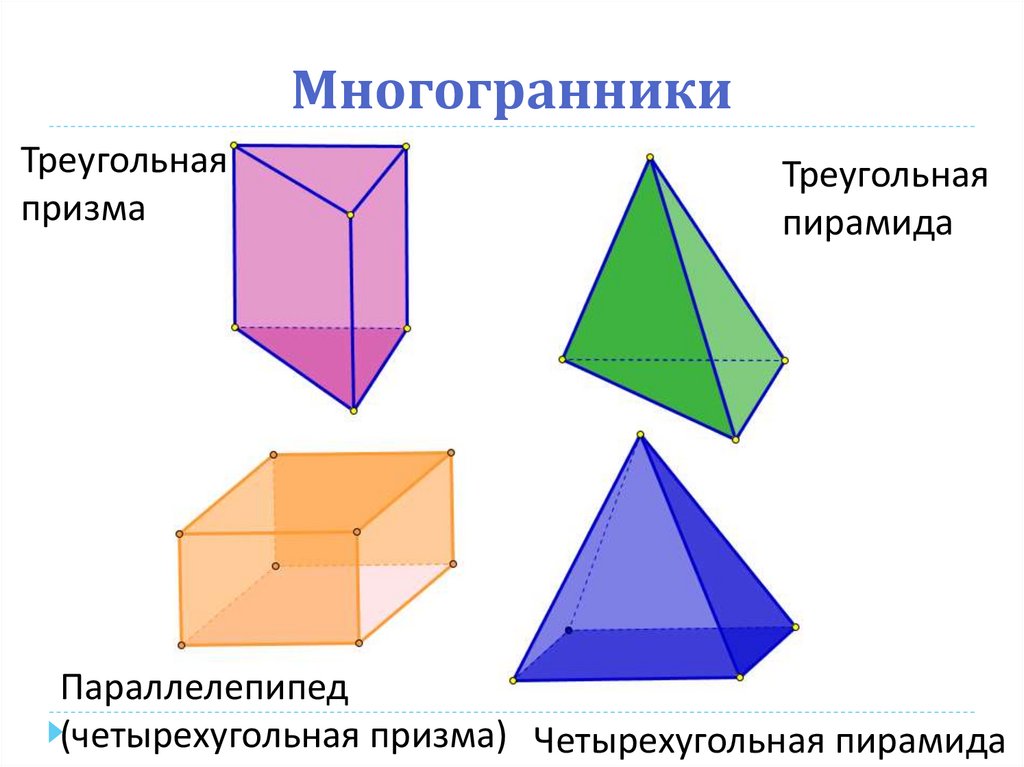
Урок 2

16. Многогранники

Треугольная
призма
Треугольная
пирамида
Параллелепипед
(четырехугольная призма) Четырехугольная пирамида

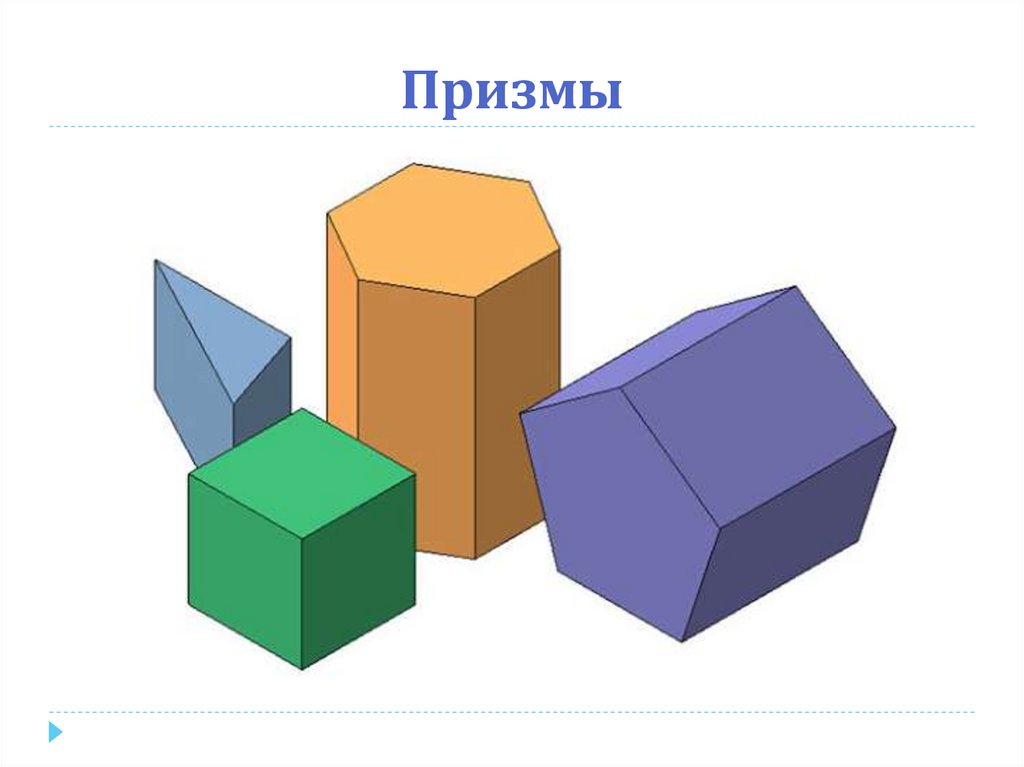
17. Призмы

18. Треугольная призма

19. Пирамиды

20. Треугольная пирамида

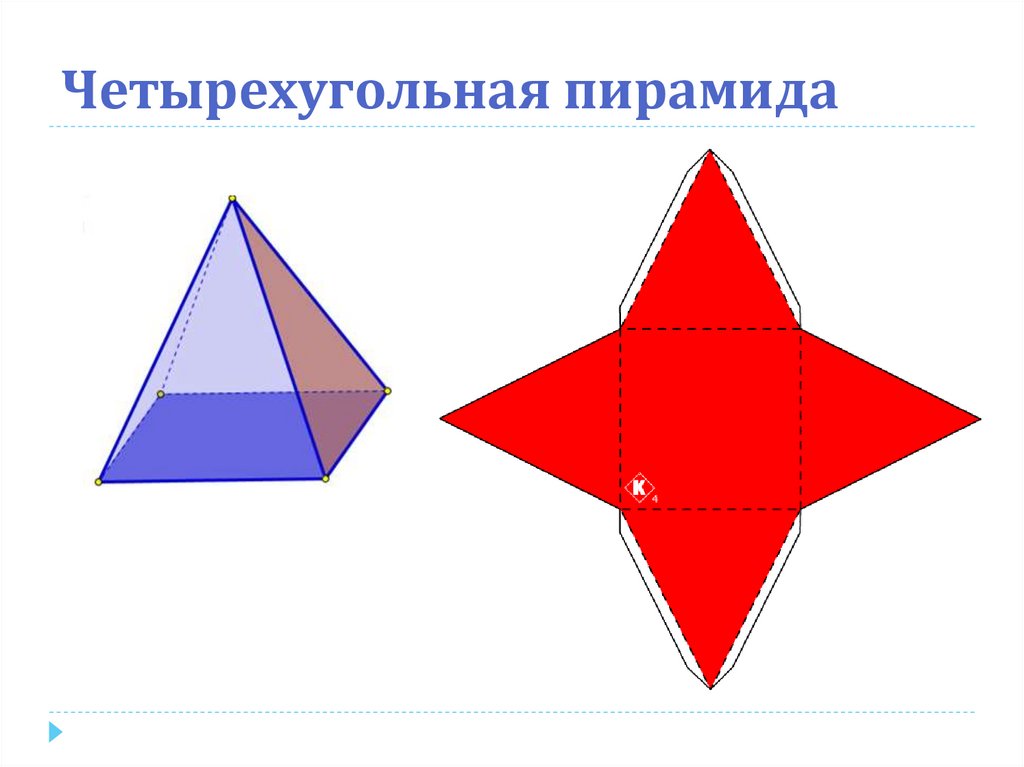
21. Четырехугольная пирамида

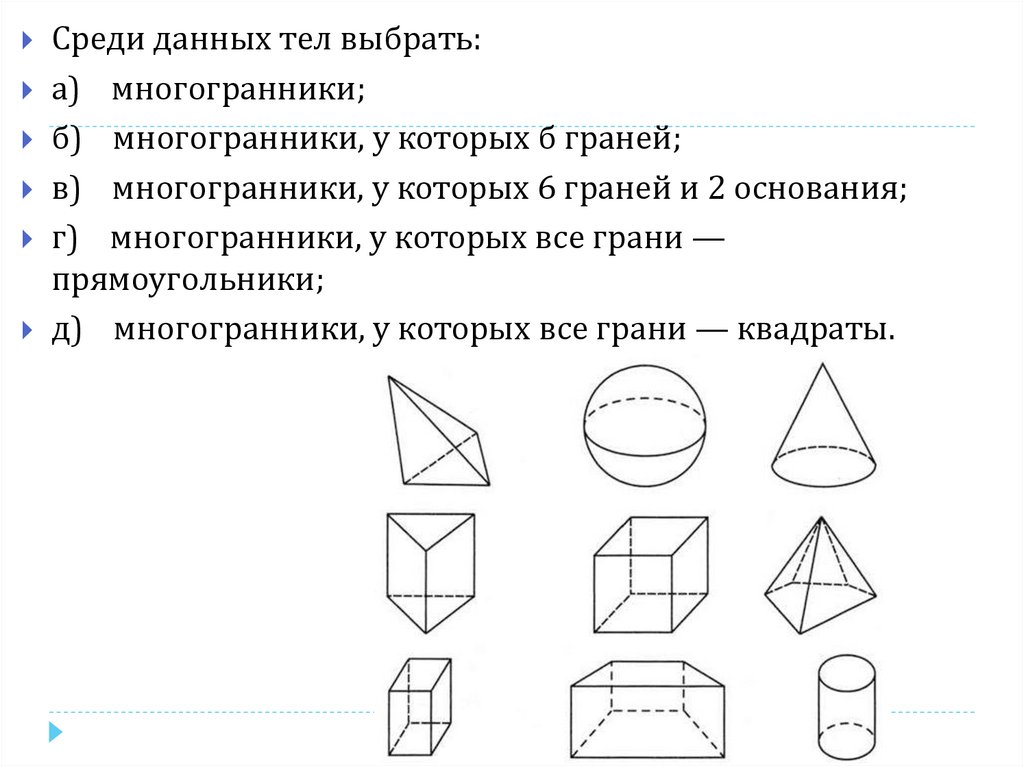
22.

Среди данных тел выбрать:
а) многогранники;
б) многогранники, у которых б граней;
в) многогранники, у которых 6 граней и 2 основания;
г) многогранники, у которых все грани —
прямоугольники;
д) многогранники, у которых все грани — квадраты.

23. Подведем итоги

Назовите тему урока.
Расскажите, чему вы научились.
С какими трудностями вы столкнулись?
Как преодолеть эти трудности?
Оцените свою деятельность на уроке: нарисуйте в своей
тетради
если всё понятно-
если некоторые задания вызвали трудности–
если ничего не понял –