Прямоугольный параллелепипед

1. СТЕРЕОМЕТРИЯ 10

§3 Двугранный угол.
Перпендикулярность плоскостей
Тема урока:
« Прямоугольный
параллелепипед»
Кузнецова Т.И.
МАОУ СОШ № 3 г.Пермь

2. Проверочная работа

Тема:
Угол между прямой и
плоскостью, угол
между плоскостями

3.

В1
С1
К1
А1
1
В
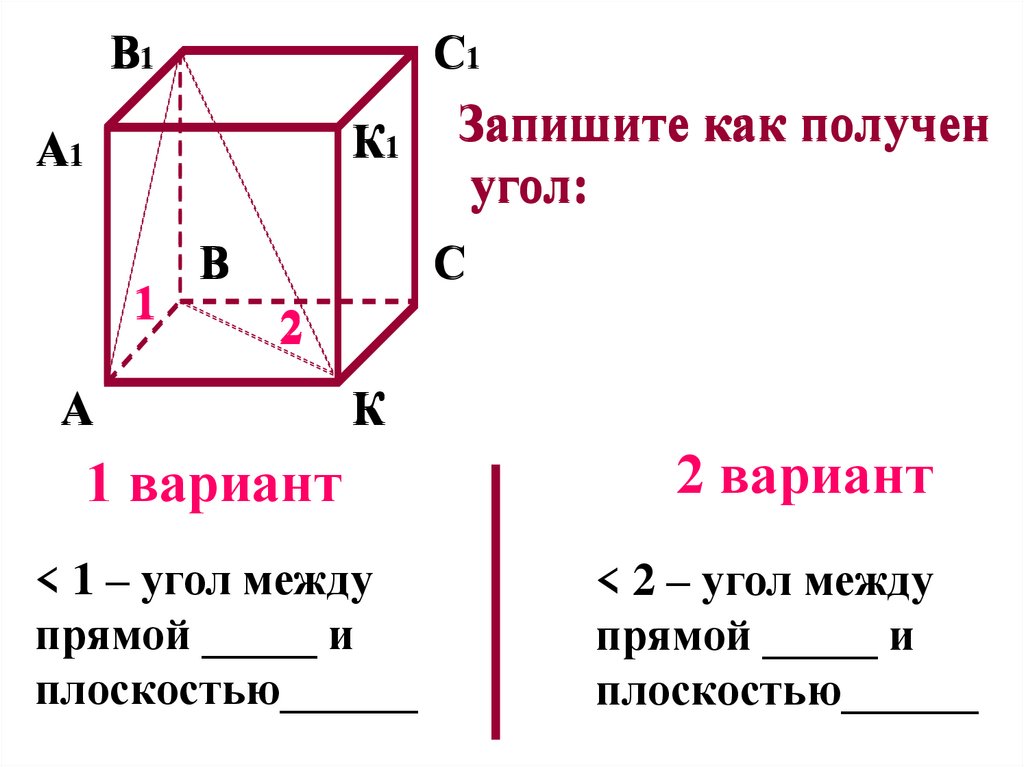
Запишите как получен
угол:
С
2
А
К
1 вариант
< 1 – угол между
прямой _____ и
плоскостью______
2 вариант
< 2 – угол между
прямой _____ и
плоскостью______

4.

В1
А1
С1
4
К1
3
В
А
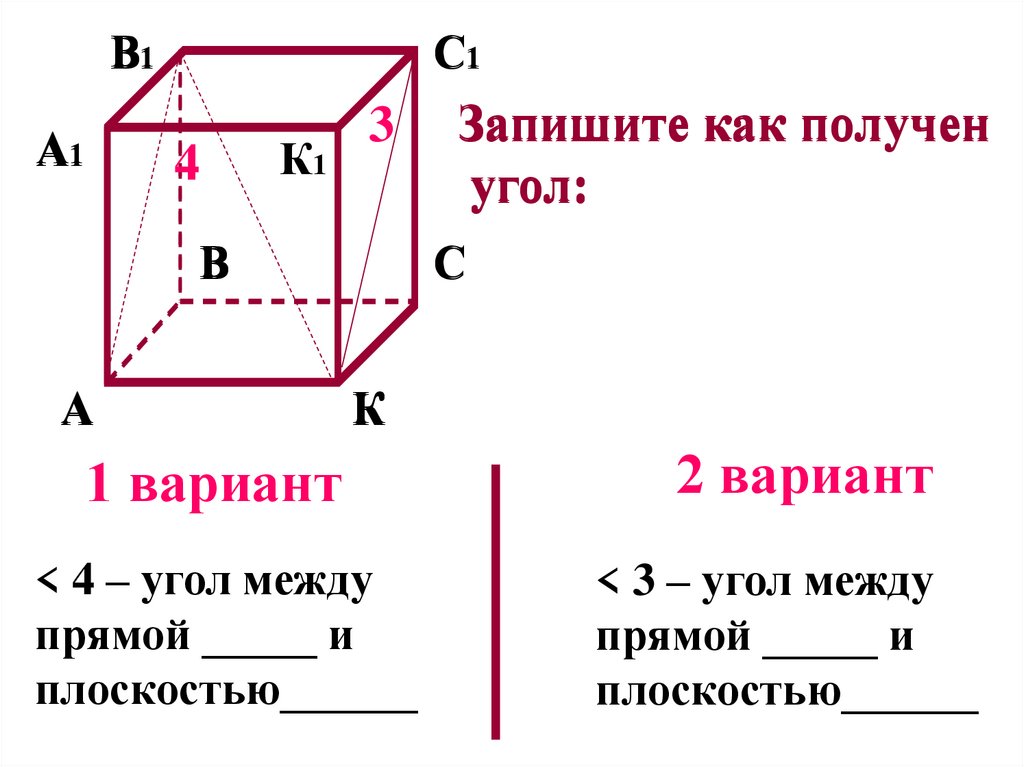
Запишите как получен
угол:
С
К
1 вариант
< 4 – угол между
прямой _____ и
плоскостью______
2 вариант
< 3 – угол между
прямой _____ и
плоскостью______

5.

В1
А1
С1
К1
С
В
А
Закончите предложение
К
1 вариант
Перпендикулярными
плоскостями
с общей точкой В
являются плоскости
_______ и _________
2 вариант
Угол между плоскостями
с общей прямой В1С1
равен _____________

6.

М1
К1
Р1
Т1
Р
М
К
КМРТК1М1Р1Т1 - куб
Т
1 вариант
Определите
величину
двугранного угла
между плоскостями
ТТ1Р1Р и КК1Т1Т.
2 вариант
Определите
величину
двугранного угла
между плоскостями
КК1Т1Т и М М1Р1Р

7.

М1
К1
Р1
Т1
Р
М
К
КМРТК1М1Р1Т1 - куб
Т
1 вариант
Определите
величину
двугранного угла
между плоскостями
ММ1Р1Р и ММ1Т1Т.
2 вариант
Определите величину
двугранного угла
между плоскостями
ММ1Т1Т и КК1Р1Р.

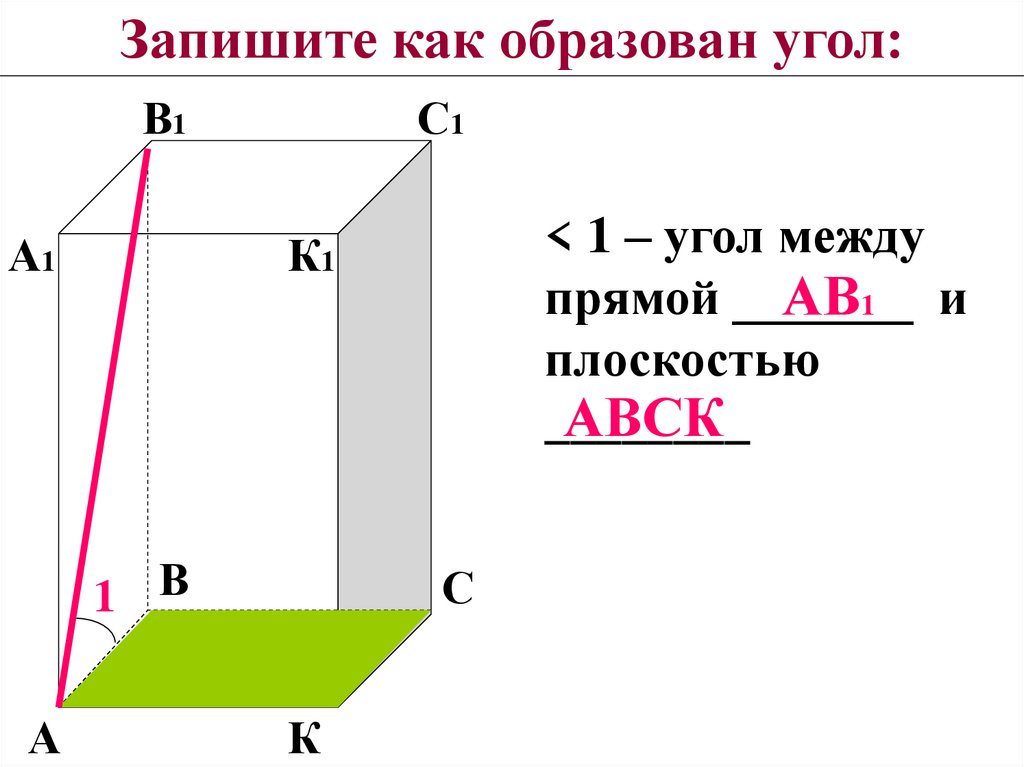
8. Запишите как образован угол:

В1
А1
С1
1 В
А
< 1 – угол между
прямой _______
АВ1 и
плоскостью
АВСК
________
К1
С
К

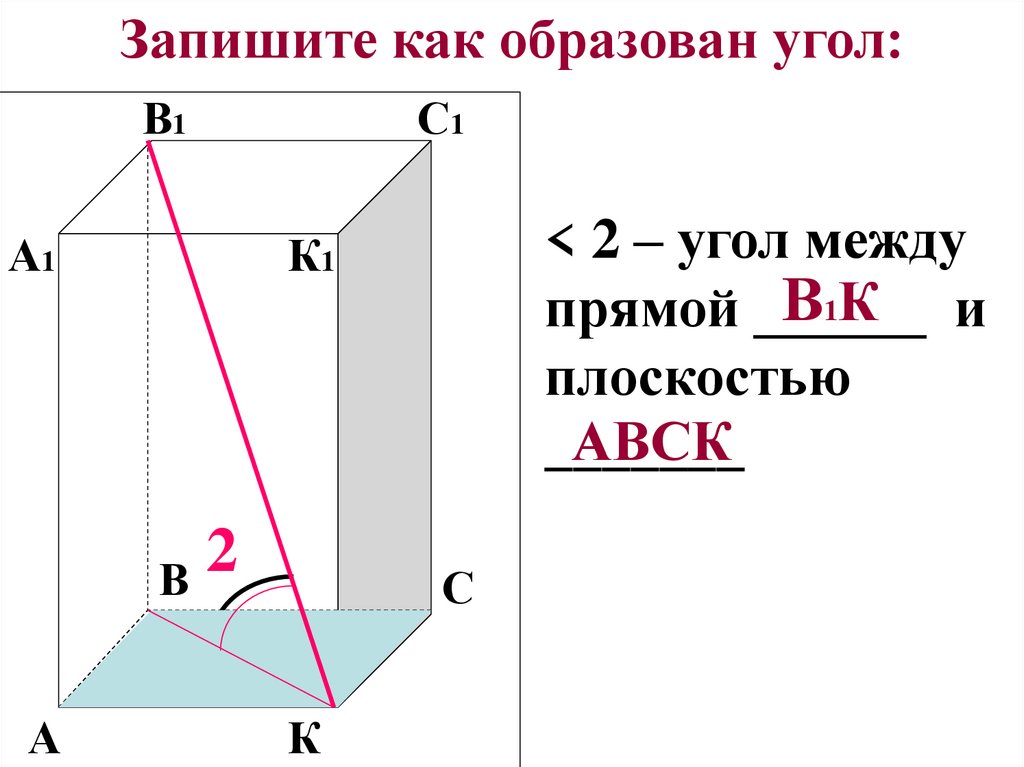
9. Запишите как образован угол:

В1
А1
С1
2
В
А
< 2 – угол между
В1 К и
прямой ______
плоскостью
АВСК
_______
К1
С
К

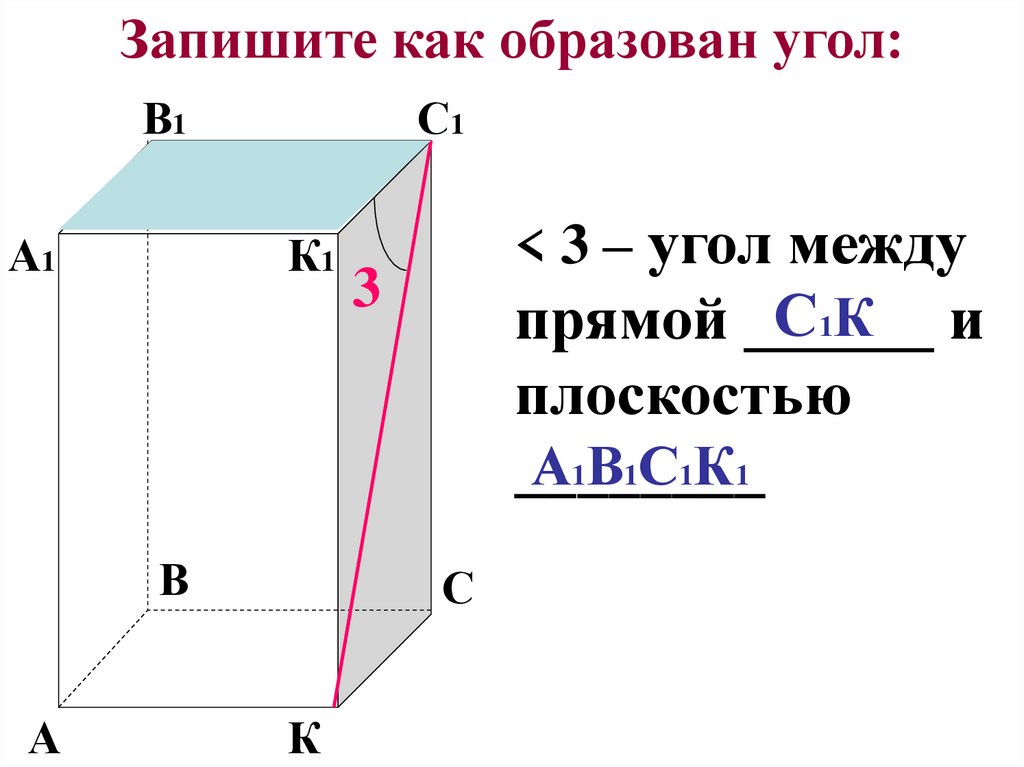
10. Запишите как образован угол:

В1
А1
С1
К1
< 3 – угол между
С1 К и
прямой ______
3
плоскостью
А1В1С1К1
________
В
А
С
К

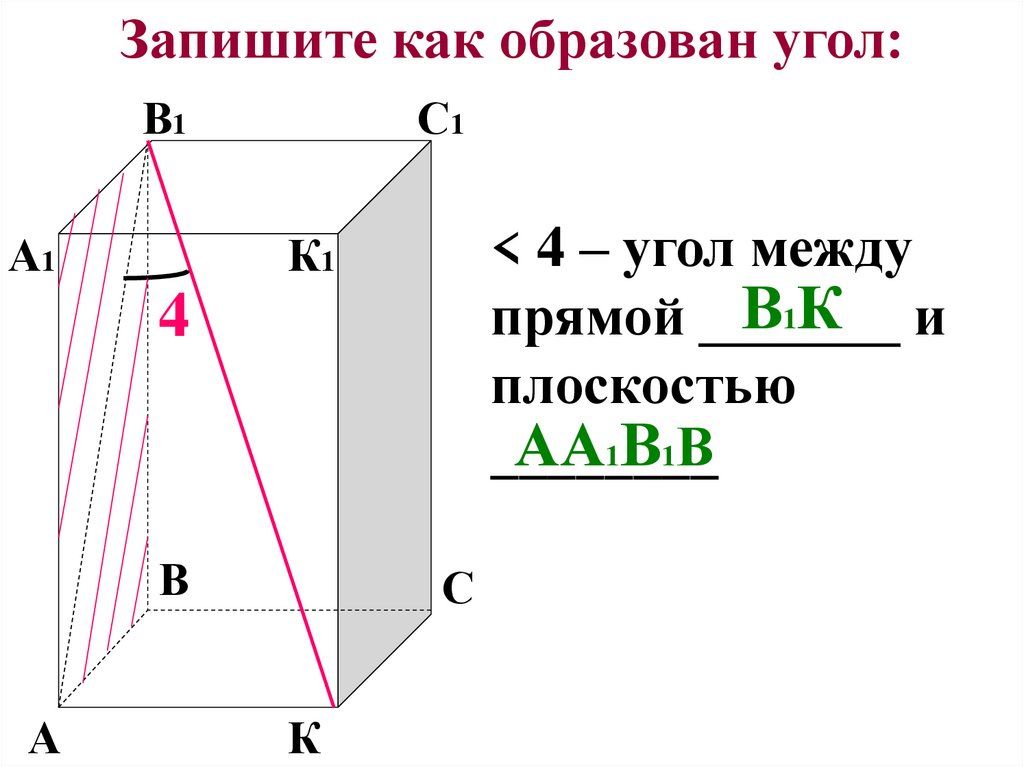
11. Запишите как образован угол:

В1
А1
С1
< 4 – угол между
В1 К и
прямой _______
плоскостью
АА1В1В
________
К1
4
В
А
С
К

12. Закончите предложение:

В1
А1
С1
К1
ВВ
А
Перпендикулярными
плоскостями с общей
точкой В являются
плоскости
__________________
ВВС1С и АВСК
С
К
АА1В1В И АВСК
__________________

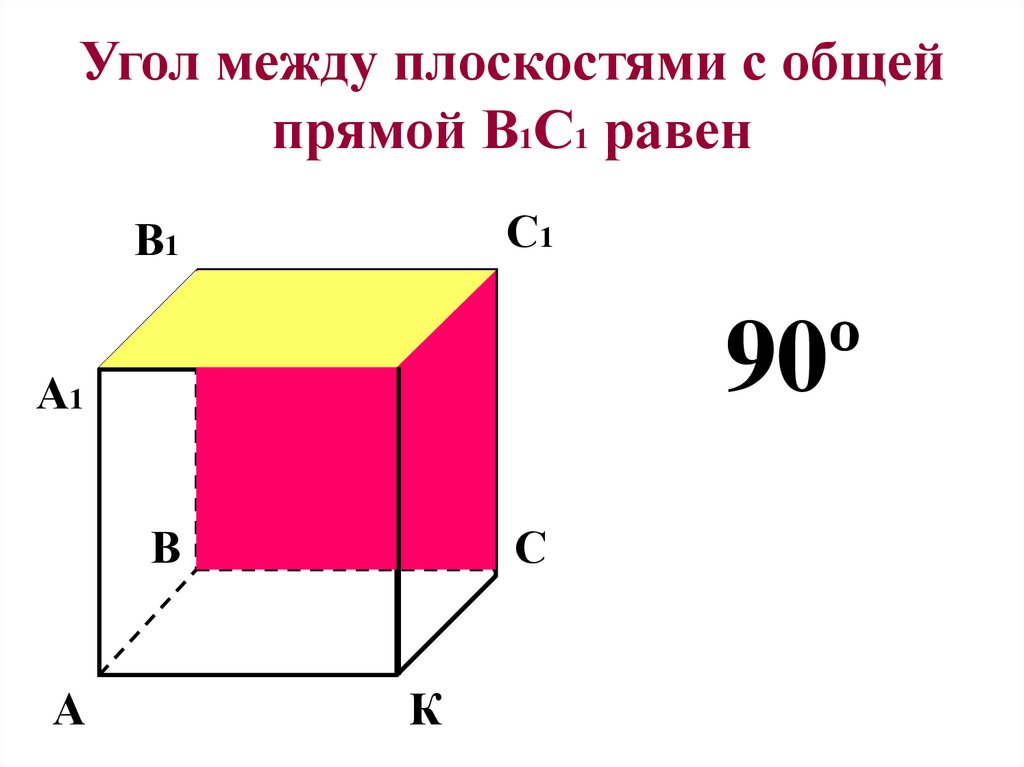
13. Угол между плоскостями с общей прямой В1С1 равен

С1
В1
В
А
90º
К1
А1
С
К

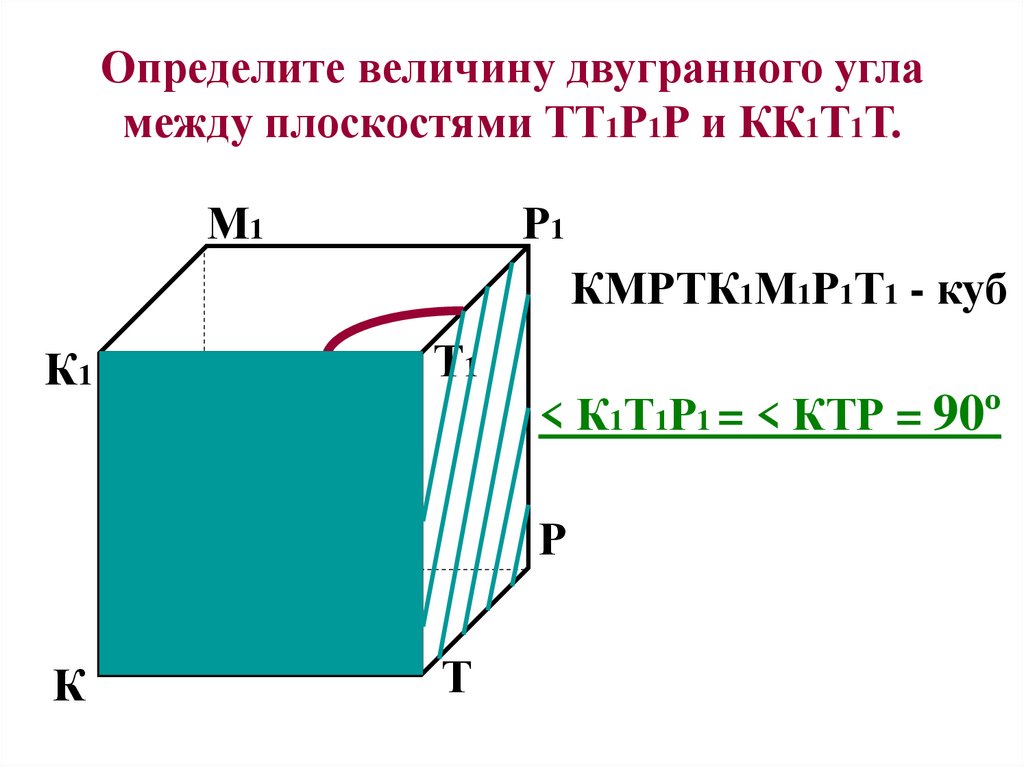
14. Определите величину двугранного угла между плоскостями ТТ1Р1Р и КК1Т1Т.

М1
Р1
КМРТК1М1Р1Т1 - куб
Т1
К1
< К1Т1Р1 = < КТР = 90º
М
К
Р
Т

15. Определите величину двугранного угла между плоскостями КК1Т1Т и М М1Р1Р

М1
Р1
КМРТК1М1Р1Т1 - куб
Т11
К1
Угол равен 0º
М
К
Р
Т

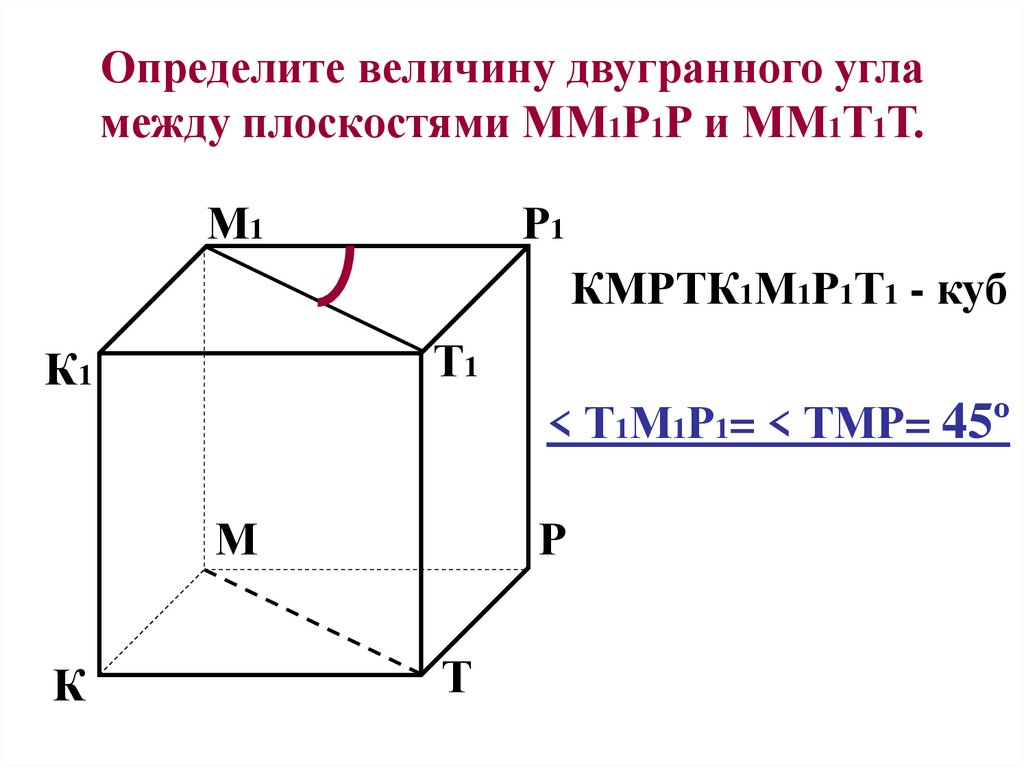
16. Определите величину двугранного угла между плоскостями ММ1Р1Р и ММ1Т1Т.

М1
Р1
КМРТК1М1Р1Т1 - куб
Т1
К1
< Т1М1Р1= < ТМР= 45º
М
К
Р
Т

17. Определите величину двугранного угла между плоскостями ММ1Т1Т и КК1Р1Р.

Р1
М1
КМРТК1М1Р1Т1 - куб
Т1
К1
Угол
равен
90º
Р
М
К
Т

18.

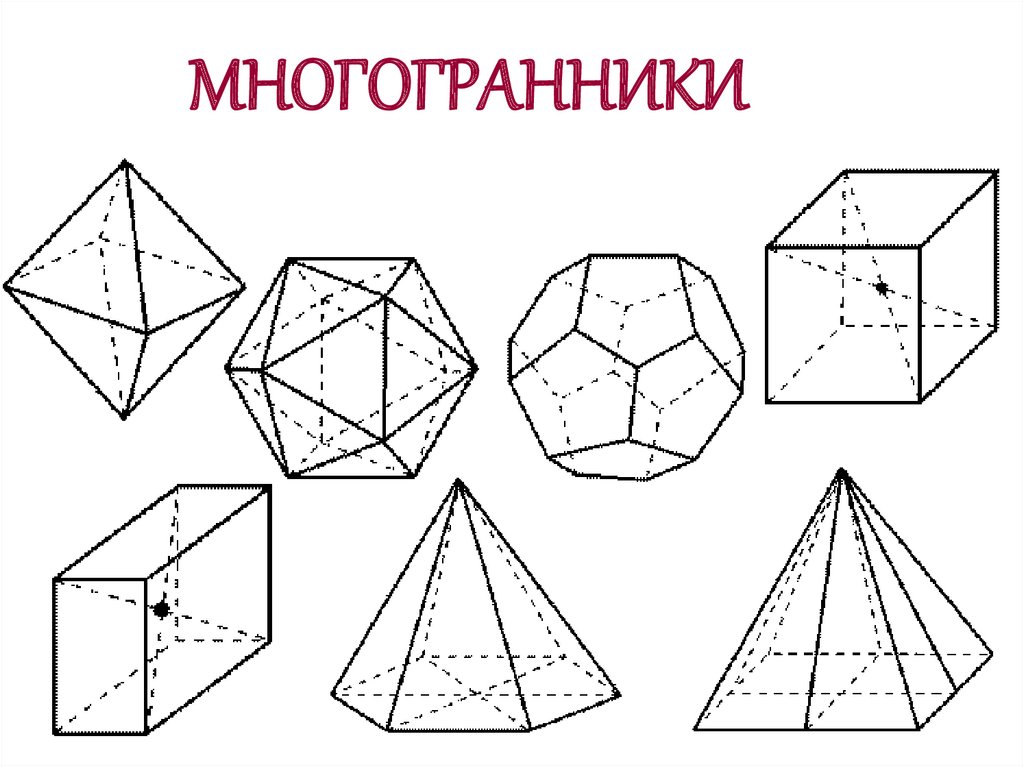
19. МНОГОГРАННИКИ

20. Поверхность, составленная из многоугольников, ограничивающих геометрическое тело, называется многогранником

21. Тема урока: Прямоугольный параллелепипед

•Вывести определение прямоугольного
параллелепипеда.
•Рассмотреть свойства прямоугольного
параллелепипеда.
•Использовать полученные знания для
решения задач.

22.

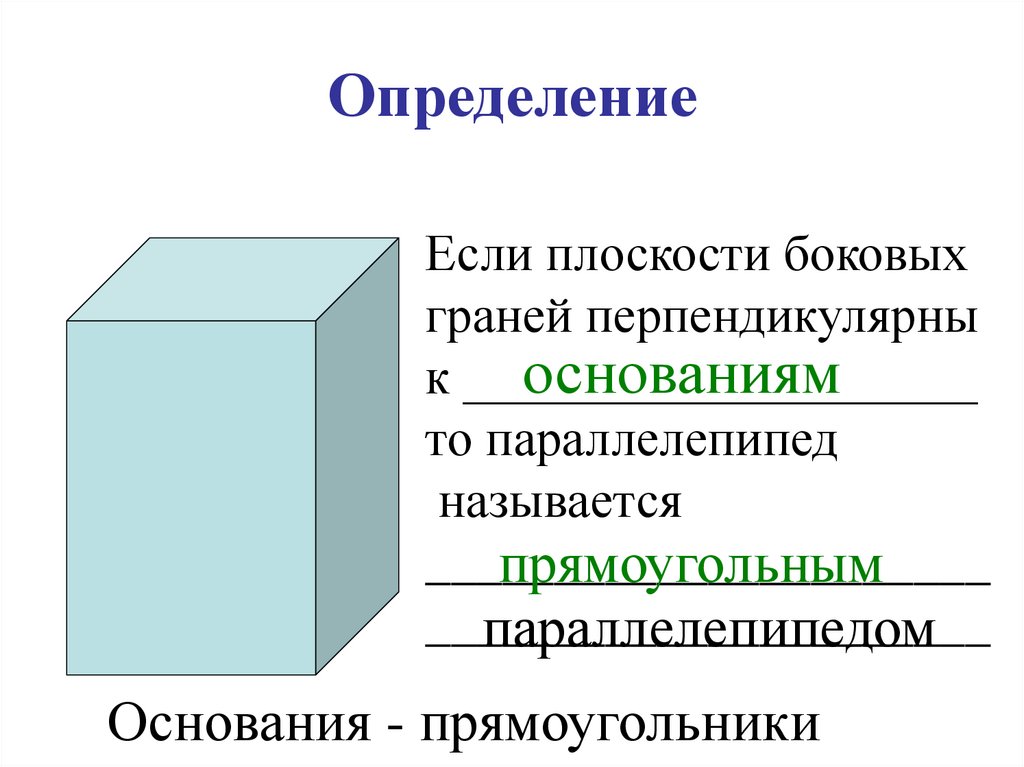
23. Определение

Если плоскости боковых
граней перпендикулярны
основаниям
к ____________________
то параллелепипед
называется
______________________
прямоугольным
______________________
параллелепипедом
Основания - прямоугольники

24.

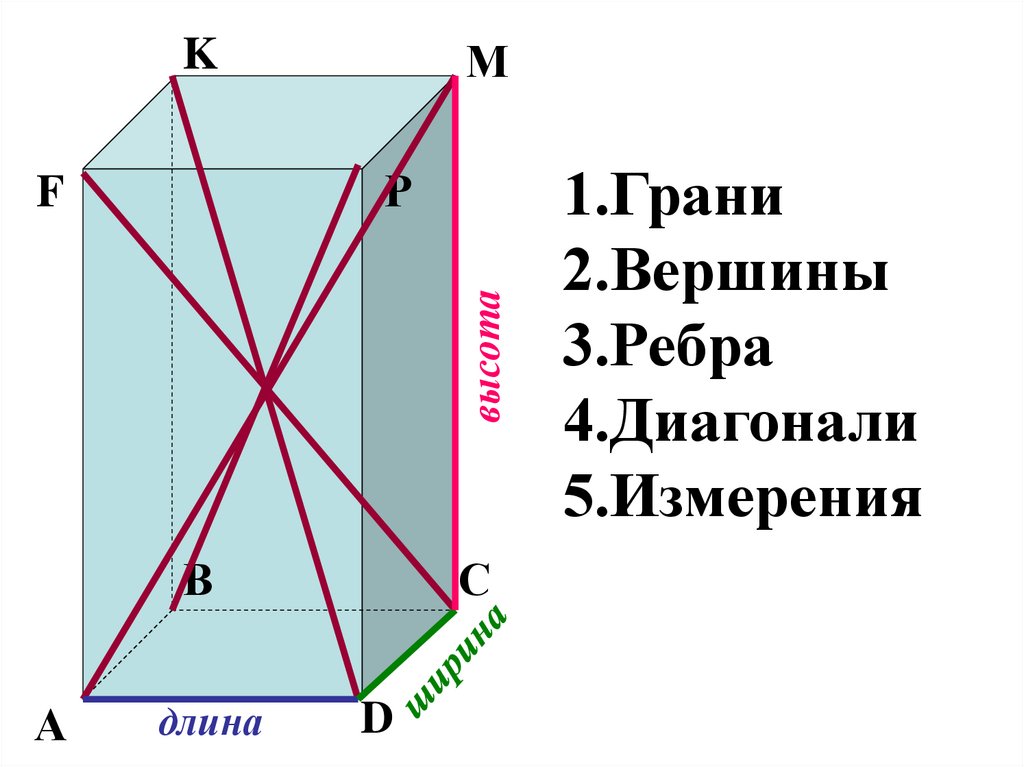
М
K
Р
высота
F
В
А
длина
С
D
1.Грани
2.Вершины
3.Ребра
4.Диагонали
5.Измерения

25.

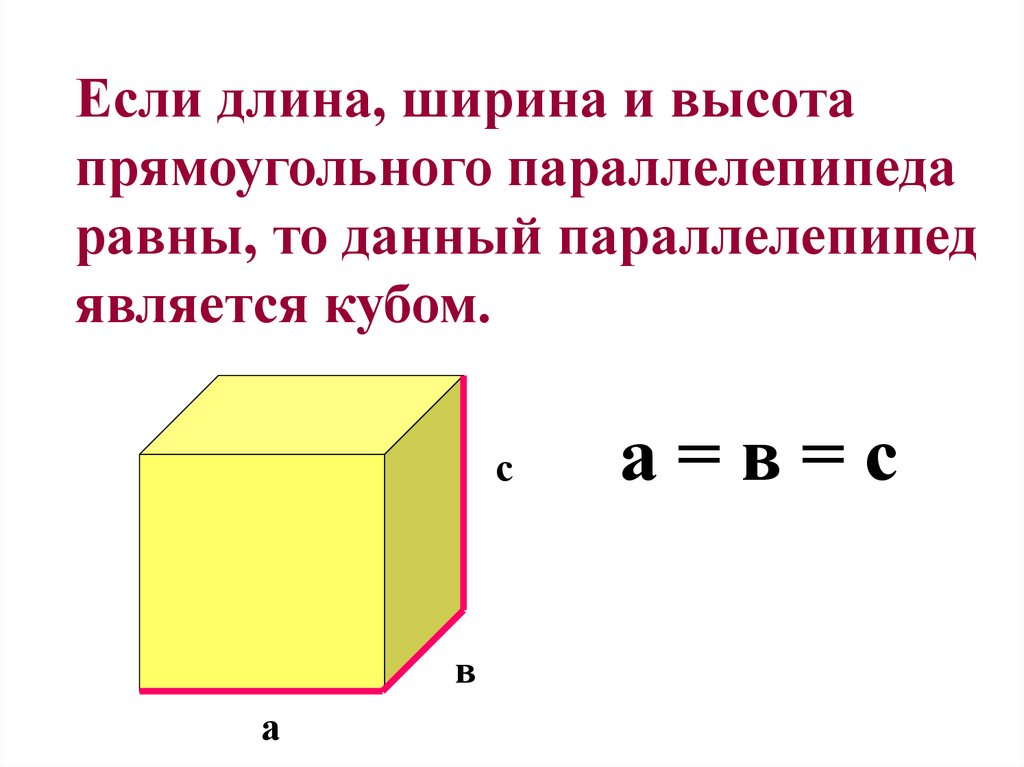
Если длина, ширина и высота
прямоугольного параллелепипеда
равны, то данный параллелепипед
является кубом.
с
в
а
а=в=с

26. Свойства прямоугольного параллелепипеда

В прямоугольном параллелепипеде
все шесть граней- прямоугольники
Все двугранные углы – прямые
Квадрат диагонали прямоугольного
параллелепипеда равен сумме
квадратов трех его измерений

27. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений

В1
А1
С1
D1
В
А
С
Из ΔАВD по теореме
Пифагора BD²= …
ВD² = AD² + AB²
D
Из ΔВВ1D по теореме Пифагора B1D²= …
В1D² = BD² + BB1
B1D²=AD²+AB²+BB1²

28. Свойства прямоугольного параллелепипеда

* В прямоугольном параллелепипеде
все шесть граней- прямоугольники
*Все двугранные углы – прямые
*Квадрат диагонали прямоугольного
параллелепипеда равен сумме
квадратов трех его измерений
*Диагонали прямоугольного
параллелепипеда равны

29.

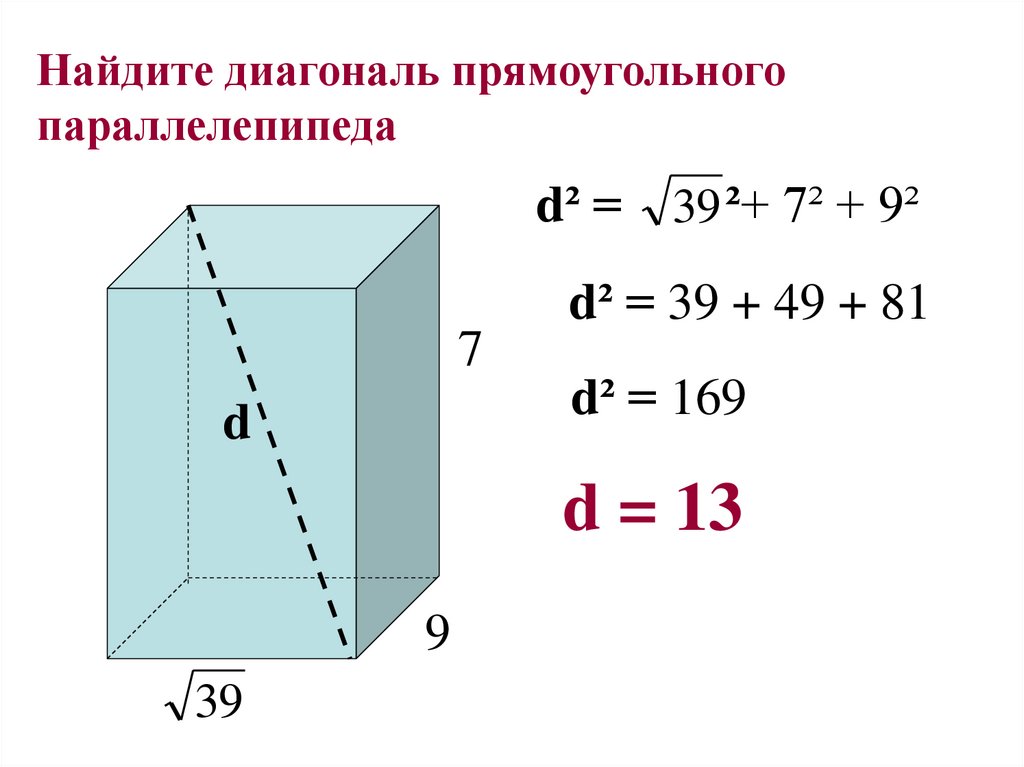
Найдите диагональ прямоугольного
параллелепипеда
d² = 39 ²+ 7² + 9²
d² = 39 + 49 + 81
7
d
d² = 169
d = 13
9
39

30.

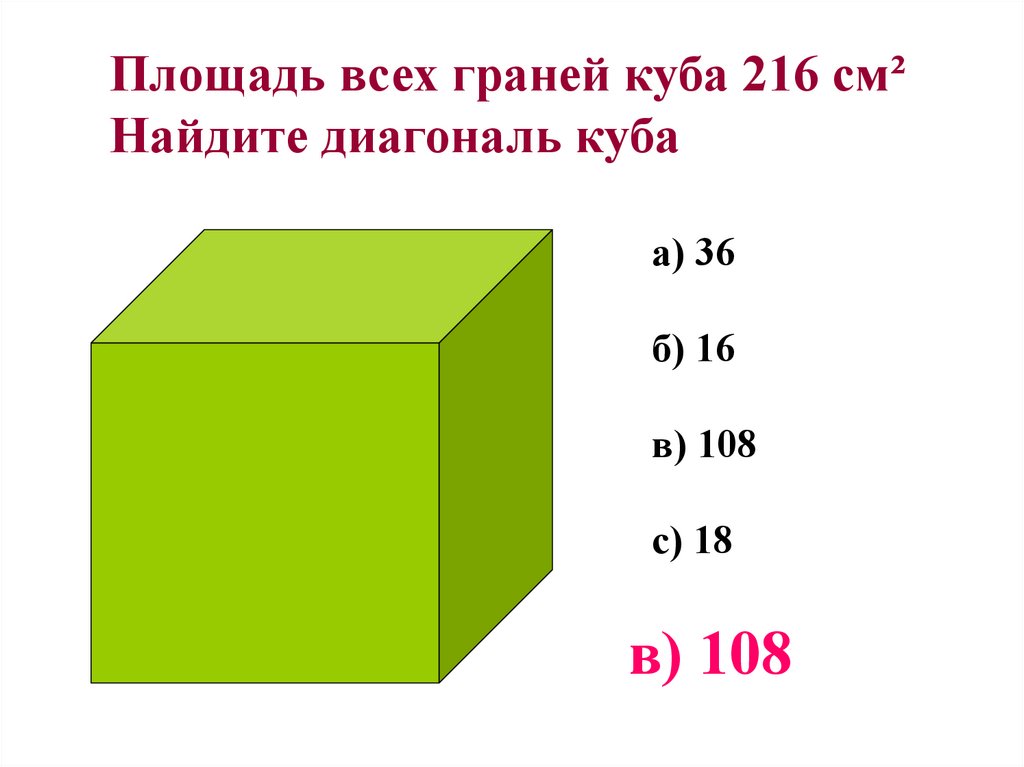
Площадь всех граней куба 216 см²
Найдите диагональ куба
а) 36
б) 16
в) 108
с) 18
в) 108

31.

В1
А1
С1
К1
С
В
А
К
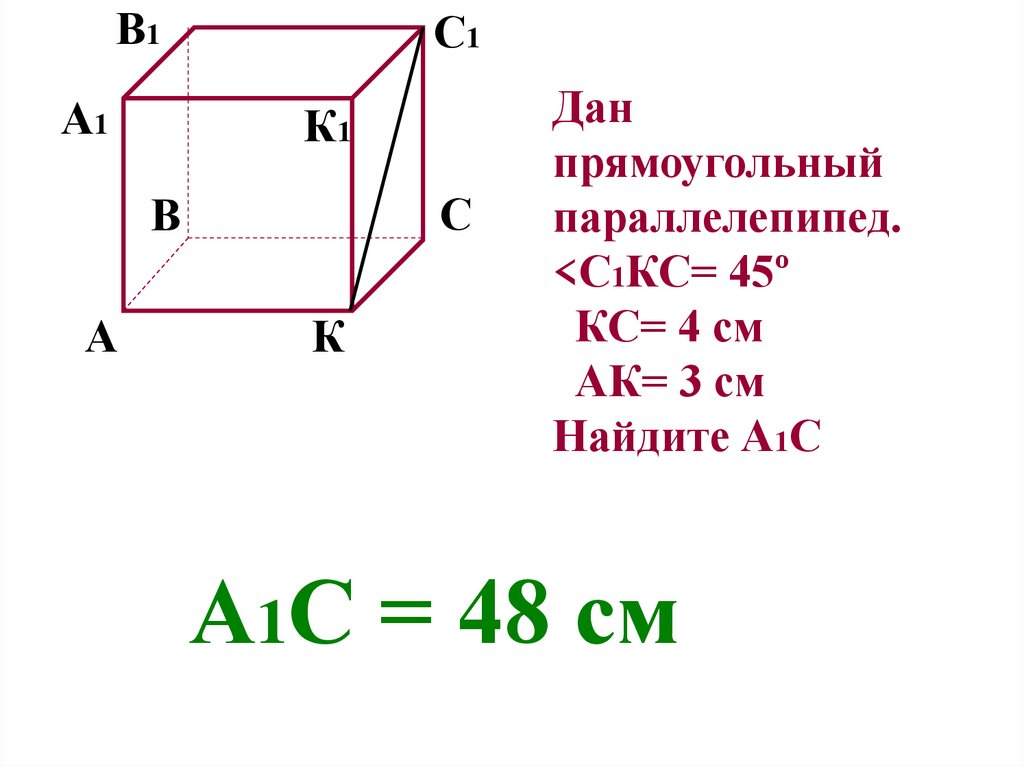
Дан
прямоугольный
параллелепипед.
<С1КС= 45º
КС= 4 см
АК= 3 см
Найдите А1С
А1С = 48 см

32.

В1
А1
С1
К1
С
В
А
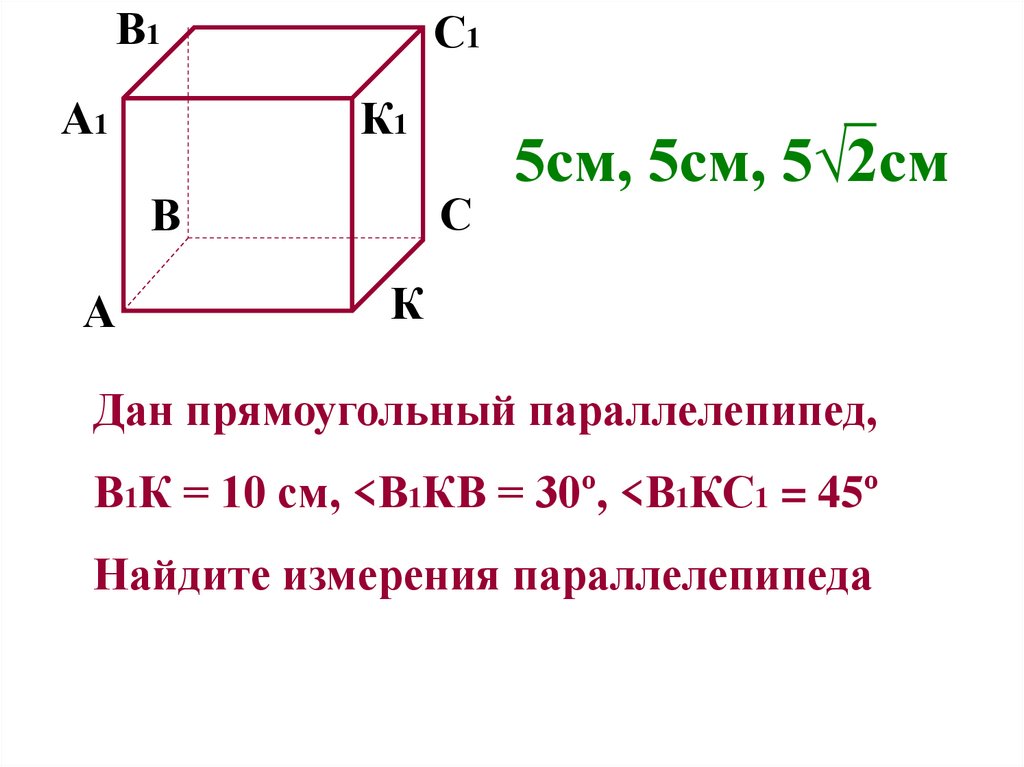
5см, 5см, 5√2см
К
Дан прямоугольный параллелепипед,
В1К = 10 см, <В1КВ = 30º, <В1КС1 = 45º
Найдите измерения параллелепипеда

33. Итог урока

• Достигнуты ли цели урока ?
Домашнее задание
п 24, задачи № 187, № 193
УСПЕХОВ!