Квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда

1. Егэ 2014

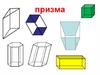
ЗАДАНИЕ В 10

2. 1. Найдите квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3.

1. НАЙДИТЕ КВАДРАТ РАССТОЯНИЯ МЕЖДУ ВЕРШИНАМИ С И
А1 ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА, ДЛЯ КОТОРОГО АВ
= 5 , AD = 4 , AA1 = 3.
B1
A1
C1
D1
3
B
C
5
5
41
A
4
D
Ответ: 50

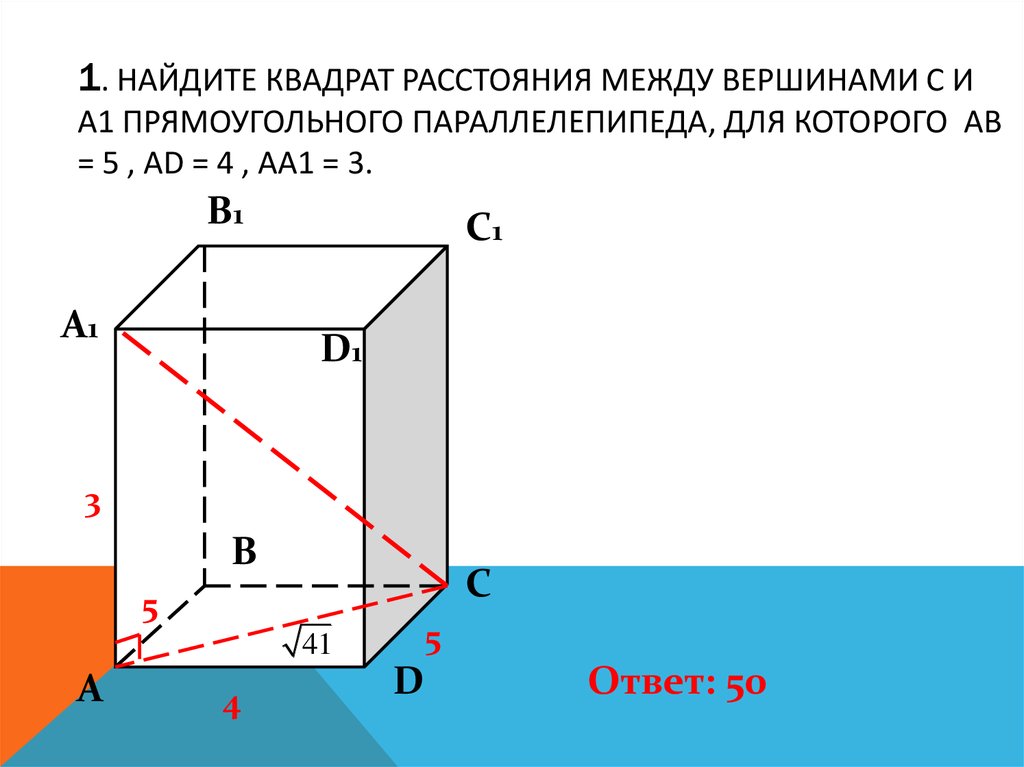
3. 2. Найдите расстояние между вершинами А и D1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3.

2. НАЙДИТЕ РАССТОЯНИЕ МЕЖДУ ВЕРШИНАМИ А И D1
ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА, ДЛЯ КОТОРОГО
АВ = 5 , AD = 4 , AA1 = 3.
B1
C1
4
A1
D1
3
B
C
5
A
4
D
Ответ: 5

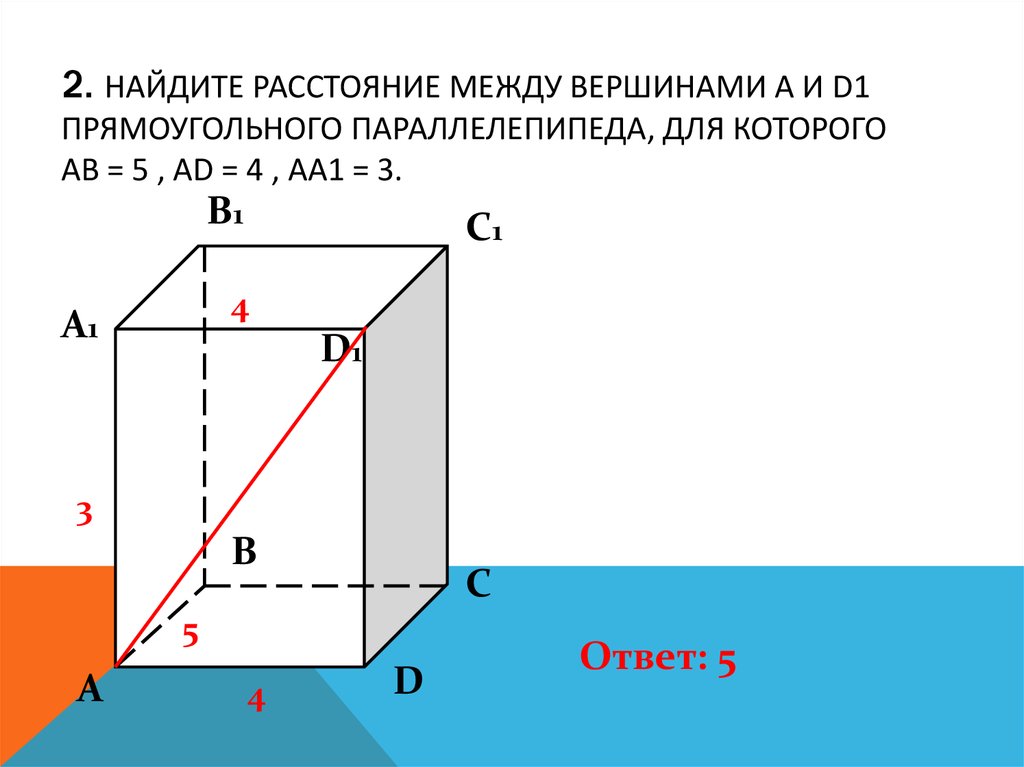
4. 3. Найдите угол ABD1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3. Ответ дайте в градусах.

3. НАЙДИТЕ УГОЛ ABD1 ПРЯМОУГОЛЬНОГО
ПАРАЛЛЕЛЕПИПЕДА, ДЛЯ КОТОРОГО АВ = 5 , AD = 4 ,
AA1 = 3. ОТВЕТ ДАЙТЕ В ГРАДУСАХ.
A1
B1
C1
D1
3
3
5
A 5
B
4
D
C
Ответ: 45

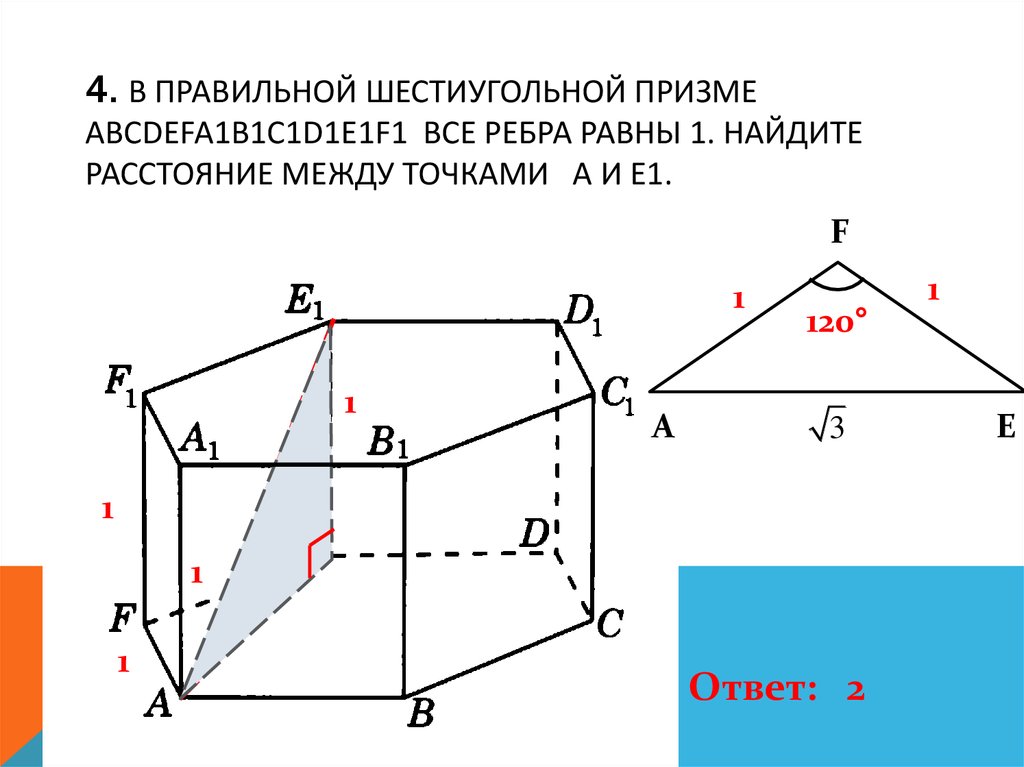
5. 4. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками A и E1.

4. В ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПРИЗМЕ
ABCDEFA1B1C1D1E1F1 ВСЕ РЕБРА РАВНЫ 1. НАЙДИТЕ
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ A И E1.
F
1
1
A
120°
3
1
1
1
3
Ответ: 2
1
E

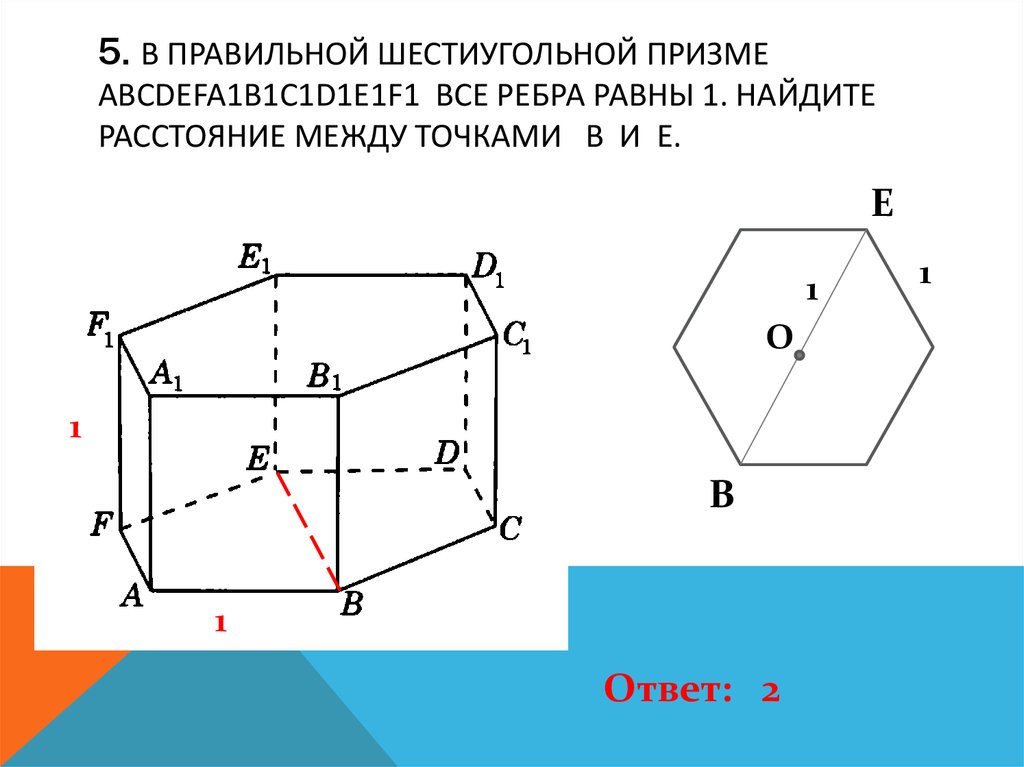
6. 5. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками B и E.

5. В ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПРИЗМЕ
ABCDEFA1B1C1D1E1F1 ВСЕ РЕБРА РАВНЫ 1. НАЙДИТЕ
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ B И E.
E
1
O
1
B
1
Ответ: 2
1

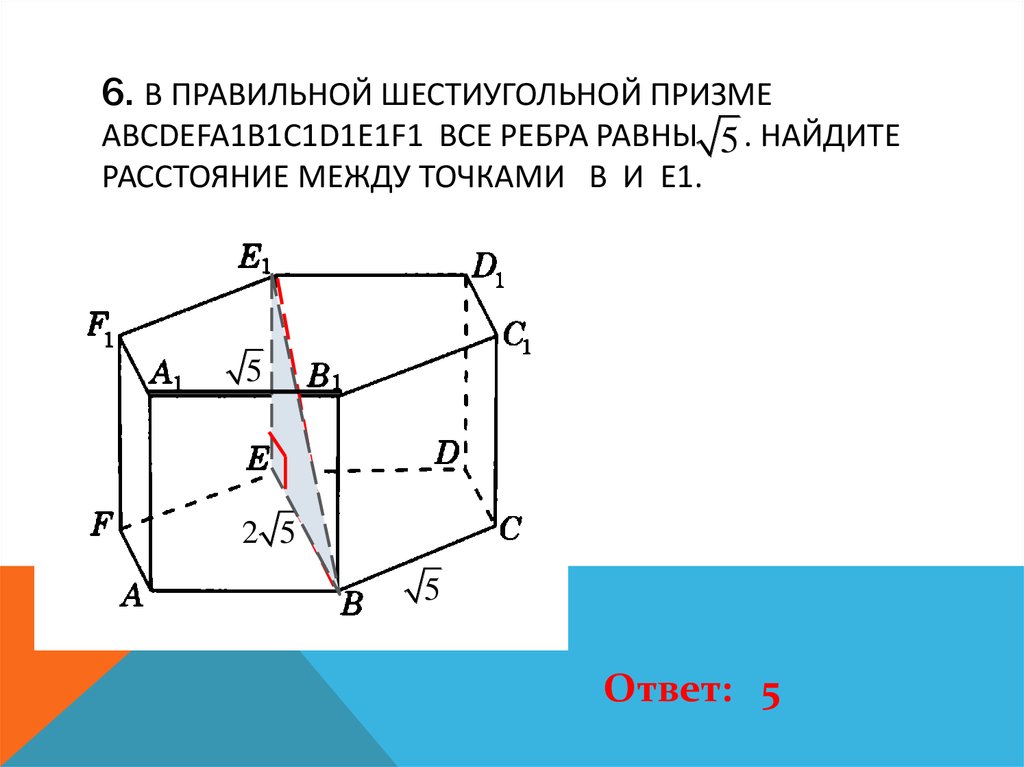
7. 6. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны . Найдите расстояние между точками B и E1.

6. В ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПРИЗМЕ
ABCDEFA1B1C1D1E1F1 ВСЕ РЕБРА РАВНЫ 5 . НАЙДИТЕ
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ B И E1.
5
2 5
5
Ответ: 5

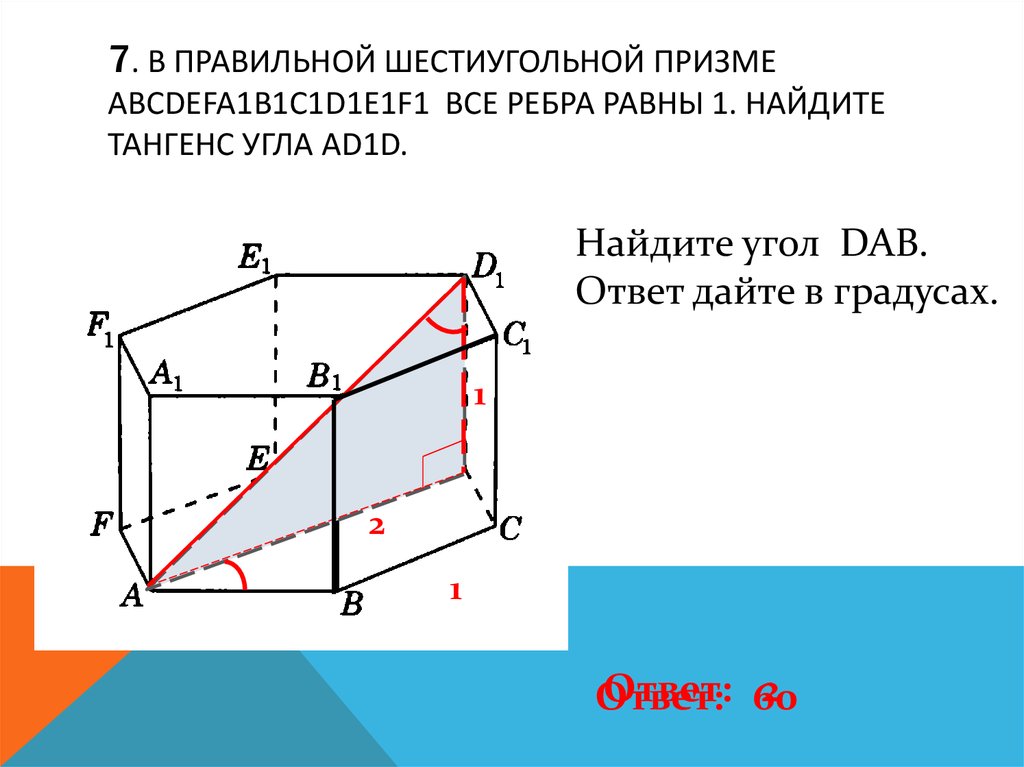
8. 7. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.

7. В ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПРИЗМЕ
ABCDEFA1B1C1D1E1F1 ВСЕ РЕБРА РАВНЫ 1. НАЙДИТЕ
ТАНГЕНС УГЛА AD1D.
Найдите угол DAB.
Ответ дайте в градусах.
1
2
1
Ответ: 60
2
Ответ:

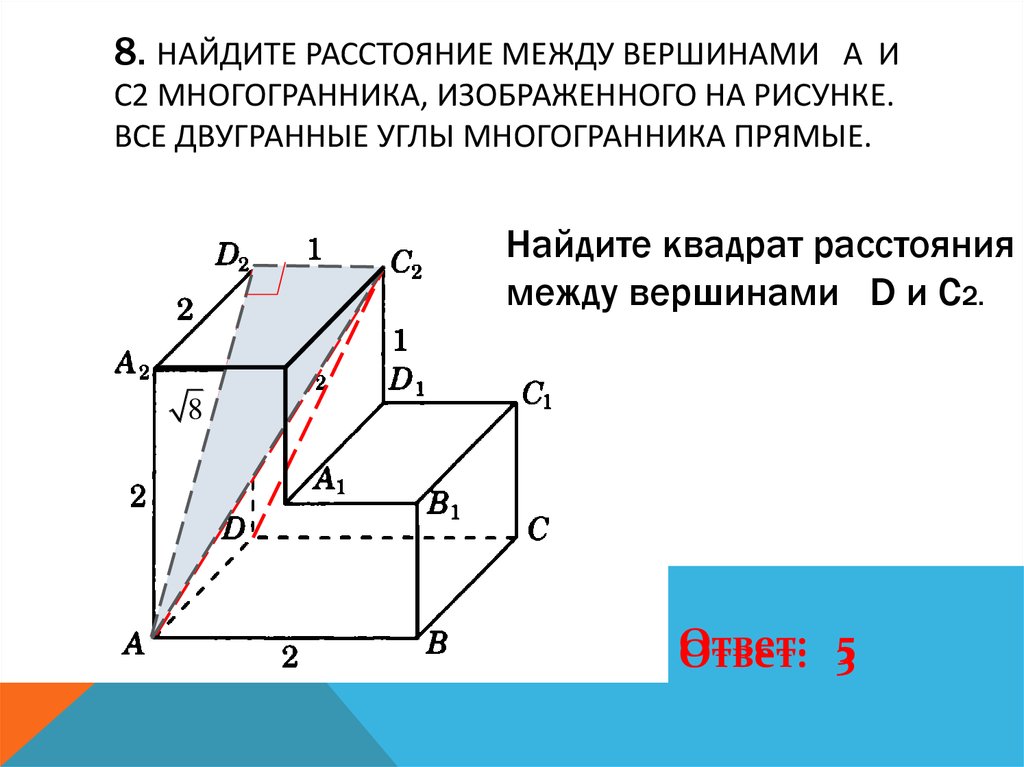
9. 8. Найдите расстояние между вершинами A и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

8. НАЙДИТЕ РАССТОЯНИЕ МЕЖДУ ВЕРШИНАМИ A И
C2 МНОГОГРАННИКА, ИЗОБРАЖЕННОГО НА РИСУНКЕ.
ВСЕ ДВУГРАННЫЕ УГЛЫ МНОГОГРАННИКА ПРЯМЫЕ.
Найдите квадрат расстояния
между вершинами D и C2.
8
Ответ:
Ответ: 53

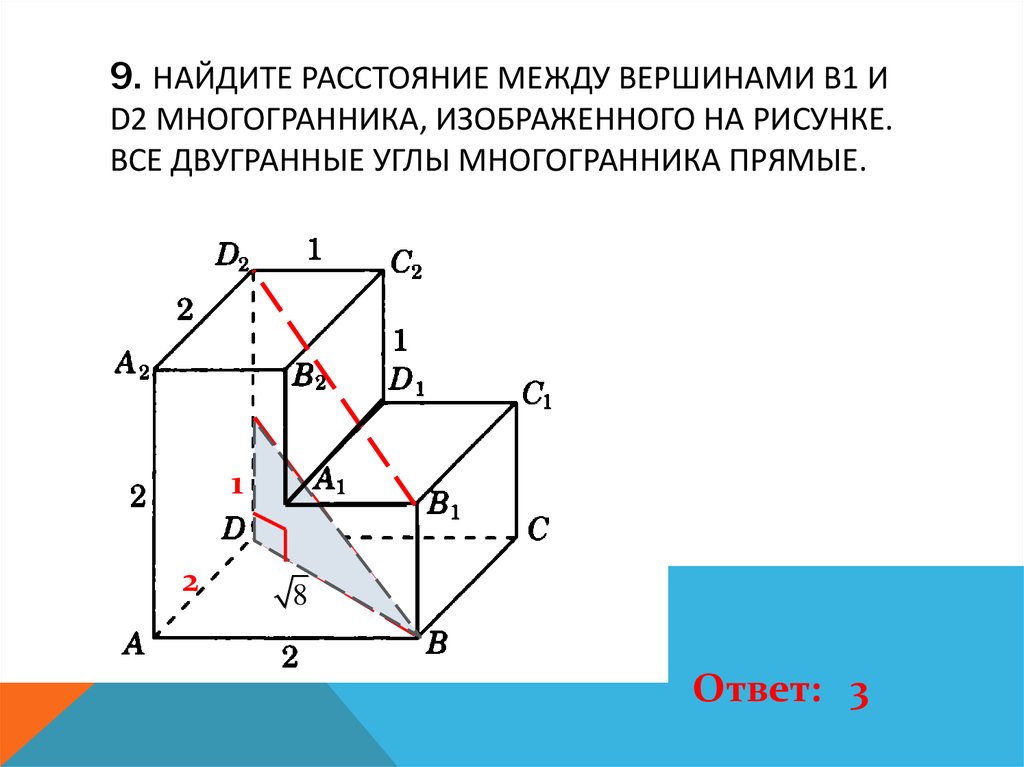
10. 9. Найдите расстояние между вершинами B1 и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника

9. НАЙДИТЕ РАССТОЯНИЕ МЕЖДУ ВЕРШИНАМИ B1 И
D2 МНОГОГРАННИКА, ИЗОБРАЖЕННОГО НА РИСУНКЕ.
ВСЕ ДВУГРАННЫЕ УГЛЫ МНОГОГРАННИКА ПРЯМЫЕ.
1
2
8
Ответ: 3

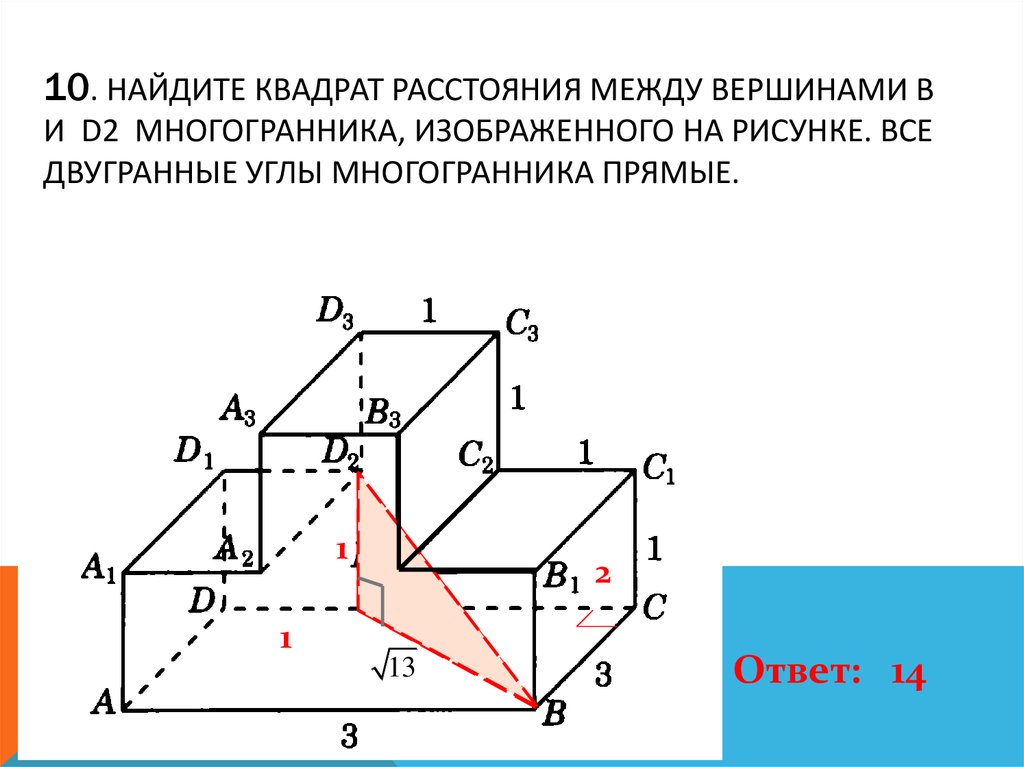
11. 10. Найдите квадрат расстояния между вершинами B и D2 многогранника, изображенного на рисунке. Все двугранные углы

10. НАЙДИТЕ КВАДРАТ РАССТОЯНИЯ МЕЖДУ ВЕРШИНАМИ B
И D2 МНОГОГРАННИКА, ИЗОБРАЖЕННОГО НА РИСУНКЕ. ВСЕ
ДВУГРАННЫЕ УГЛЫ МНОГОГРАННИКА ПРЯМЫЕ.
1
2
1
13
Ответ: 14

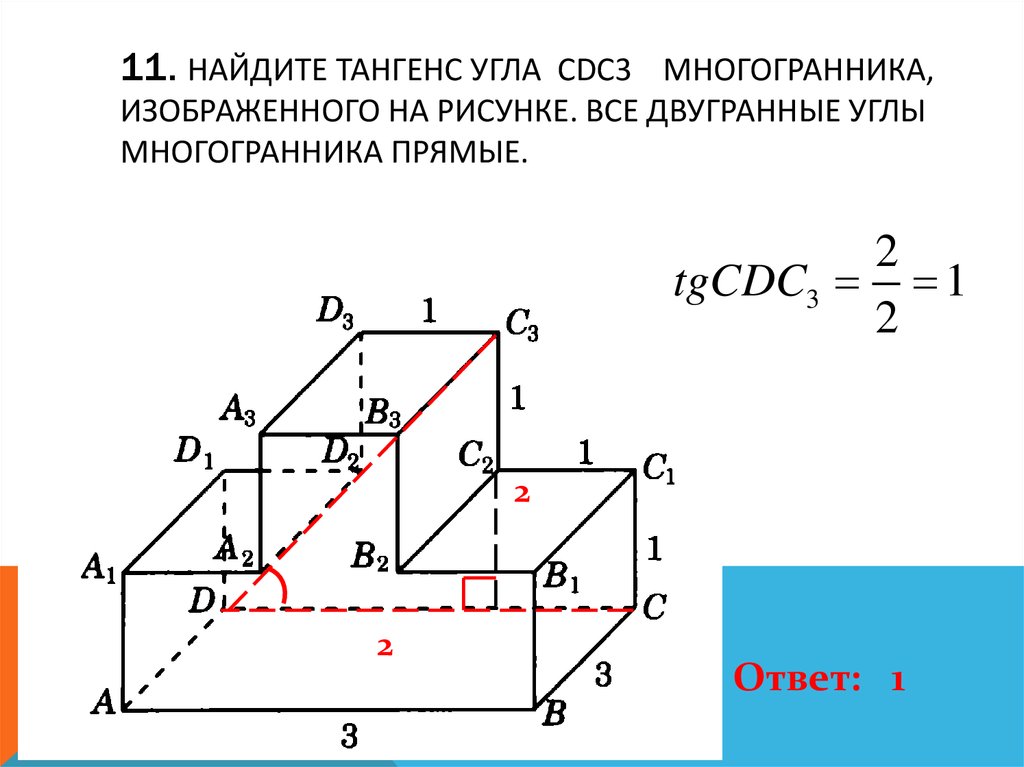
12. 11. Найдите тангенс угла CDC3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

11. НАЙДИТЕ ТАНГЕНС УГЛА CDC3 МНОГОГРАННИКА,
ИЗОБРАЖЕННОГО НА РИСУНКЕ. ВСЕ ДВУГРАННЫЕ УГЛЫ
МНОГОГРАННИКА ПРЯМЫЕ.
2
tgCDC3 1
2
2
2
Ответ: 1

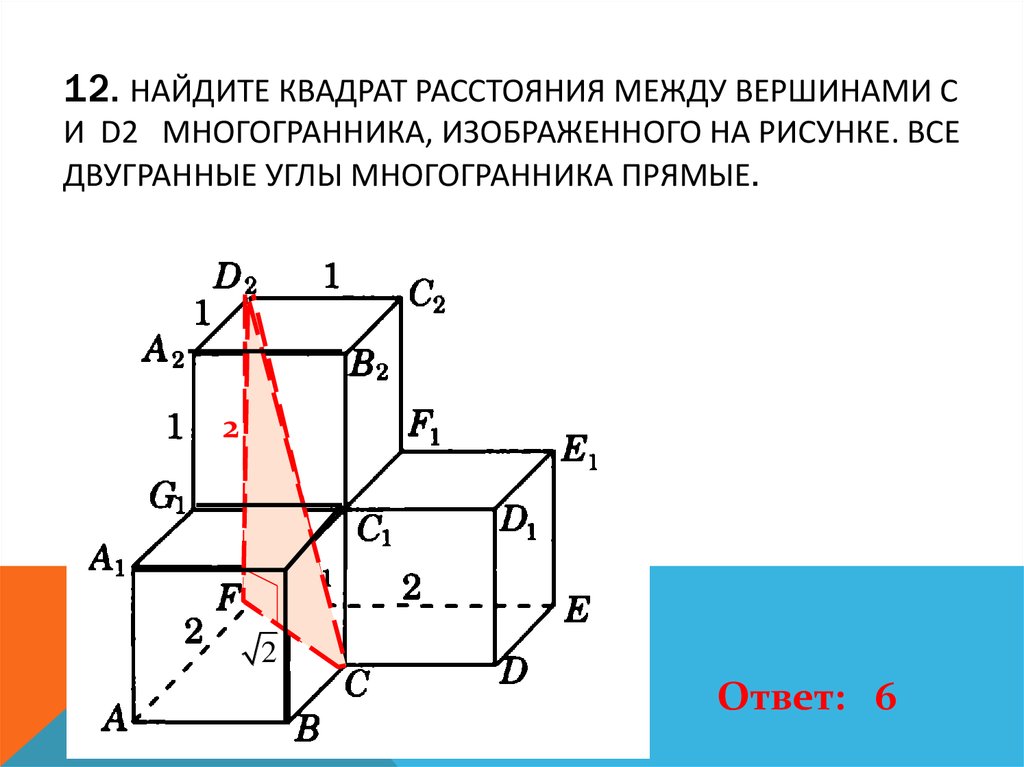
13. 12. Найдите квадрат расстояния между вершинами C и D2 многогранника, изображенного на рисунке. Все двугранные углы

12. НАЙДИТЕ КВАДРАТ РАССТОЯНИЯ МЕЖДУ ВЕРШИНАМИ C
И D2 МНОГОГРАННИКА, ИЗОБРАЖЕННОГО НА РИСУНКЕ. ВСЕ
ДВУГРАННЫЕ УГЛЫ МНОГОГРАННИКА ПРЯМЫЕ.
2
2
Ответ: 6

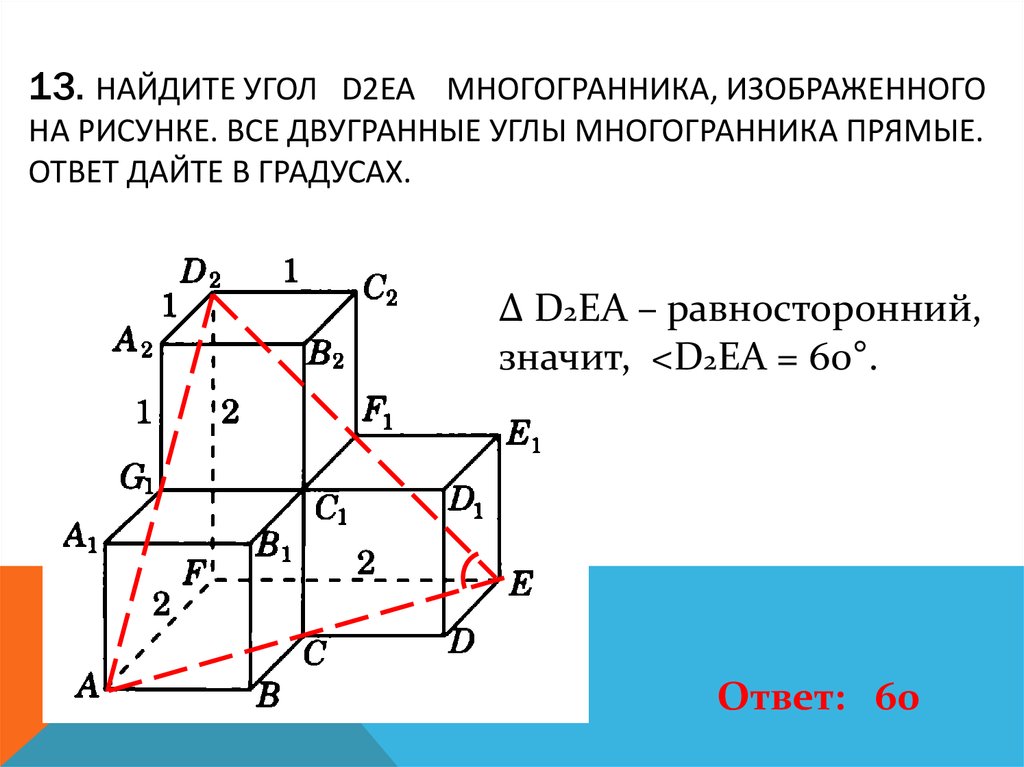
14. 13. Найдите угол D2EA многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в

13. НАЙДИТЕ УГОЛ D2EA МНОГОГРАННИКА, ИЗОБРАЖЕННОГО
НА РИСУНКЕ. ВСЕ ДВУГРАННЫЕ УГЛЫ МНОГОГРАННИКА ПРЯМЫЕ.
ОТВЕТ ДАЙТЕ В ГРАДУСАХ.
Δ D2EA – равносторонний,
значит, <D2EA = 60°.
Ответ: 60

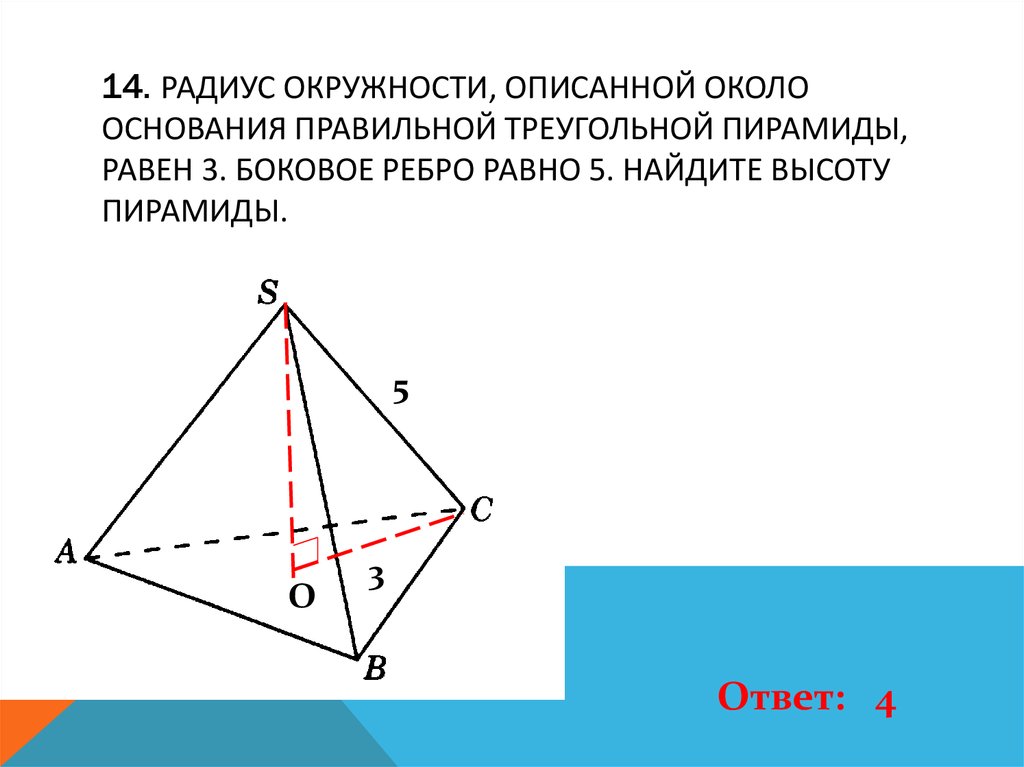
15. 14. Радиус окружности, описанной около основания правильной треугольной пирамиды, равен 3. боковое ребро равно 5. Найдите

14. РАДИУС ОКРУЖНОСТИ, ОПИСАННОЙ ОКОЛО
ОСНОВАНИЯ ПРАВИЛЬНОЙ ТРЕУГОЛЬНОЙ ПИРАМИДЫ,
РАВЕН 3. БОКОВОЕ РЕБРО РАВНО 5. НАЙДИТЕ ВЫСОТУ
ПИРАМИДЫ.
5
О
3
Ответ: 4

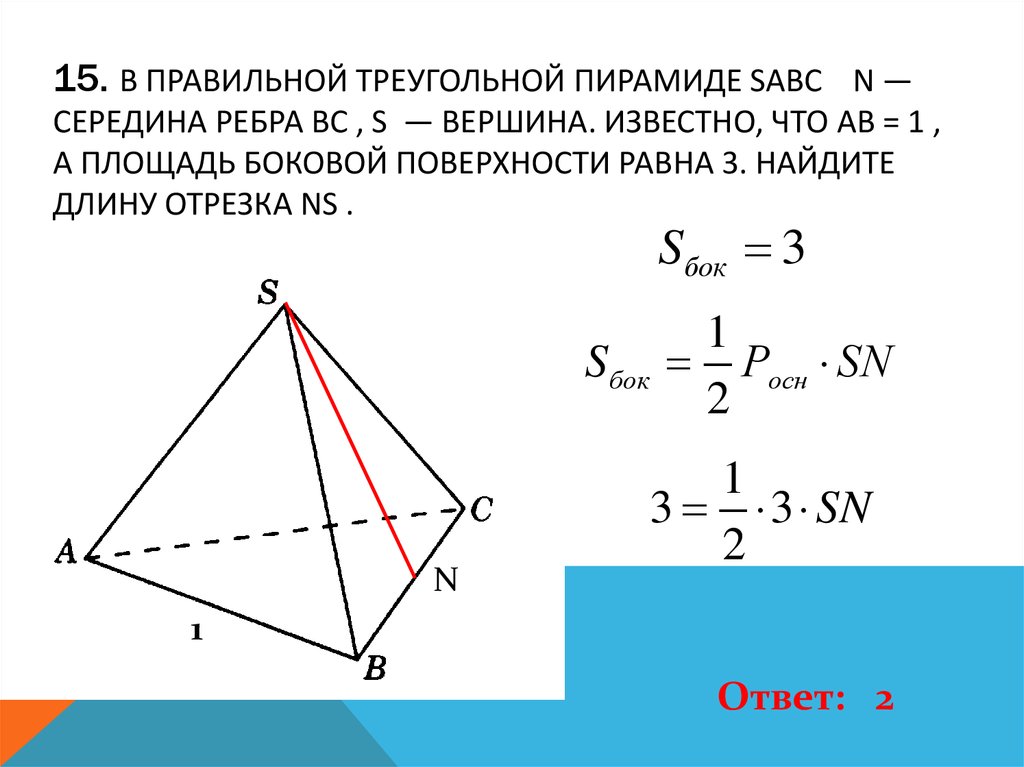
16. 15. В правильной треугольной пирамиде SABC N — середина ребра BC , S  — вершина. Известно, что AB = 1 , а площадь боковой

15. В ПРАВИЛЬНОЙ ТРЕУГОЛЬНОЙ ПИРАМИДЕ SABC N —
СЕРЕДИНА РЕБРА BC , S — ВЕРШИНА. ИЗВЕСТНО, ЧТО AB = 1 ,
А ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ РАВНА 3. НАЙДИТЕ
ДЛИНУ ОТРЕЗКА NS .
Sбок 3
Sбок
N
1
Росн SN
2
1
3 3 SN
2
1
Ответ: 2

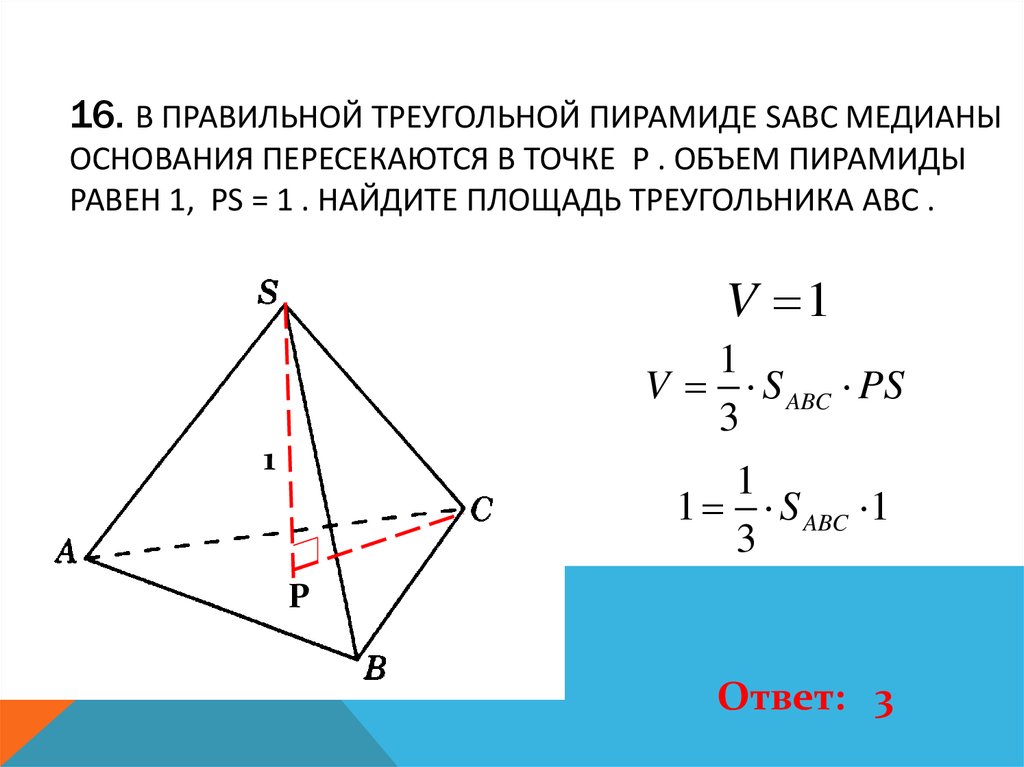
17. 16. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке P . Объем пирамиды равен 1, PS = 1 . Найдите

16. В ПРАВИЛЬНОЙ ТРЕУГОЛЬНОЙ ПИРАМИДЕ SABC МЕДИАНЫ
ОСНОВАНИЯ ПЕРЕСЕКАЮТСЯ В ТОЧКЕ P . ОБЪЕМ ПИРАМИДЫ
РАВЕН 1, PS = 1 . НАЙДИТЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКА ABC .
V 1
1
V S ABC PS
3
1
1
1 S ABC 1
3
P
Ответ: 3

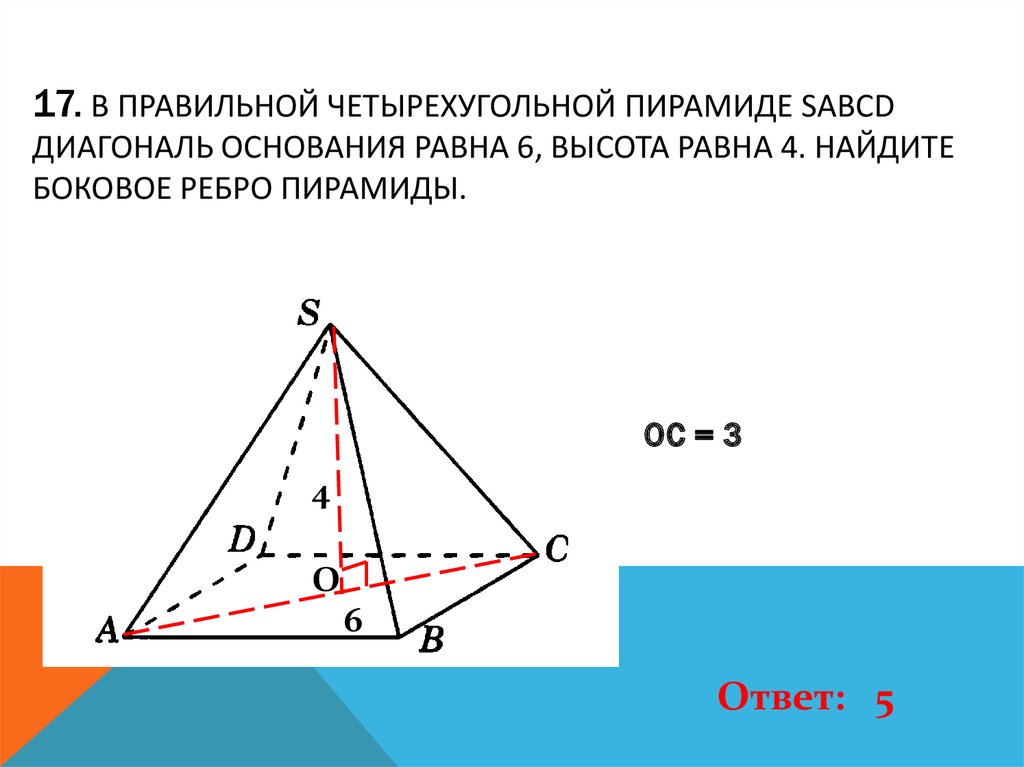
18. 17. В правильной четырехугольной пирамиде SABCD диагональ основания равна 6, высота равна 4. Найдите боковое ребро пирамиды.

17. В ПРАВИЛЬНОЙ ЧЕТЫРЕХУГОЛЬНОЙ ПИРАМИДЕ SABCD
ДИАГОНАЛЬ ОСНОВАНИЯ РАВНА 6, ВЫСОТА РАВНА 4. НАЙДИТЕ
БОКОВОЕ РЕБРО ПИРАМИДЫ.
ОС = 3
4
О
6
Ответ: 5

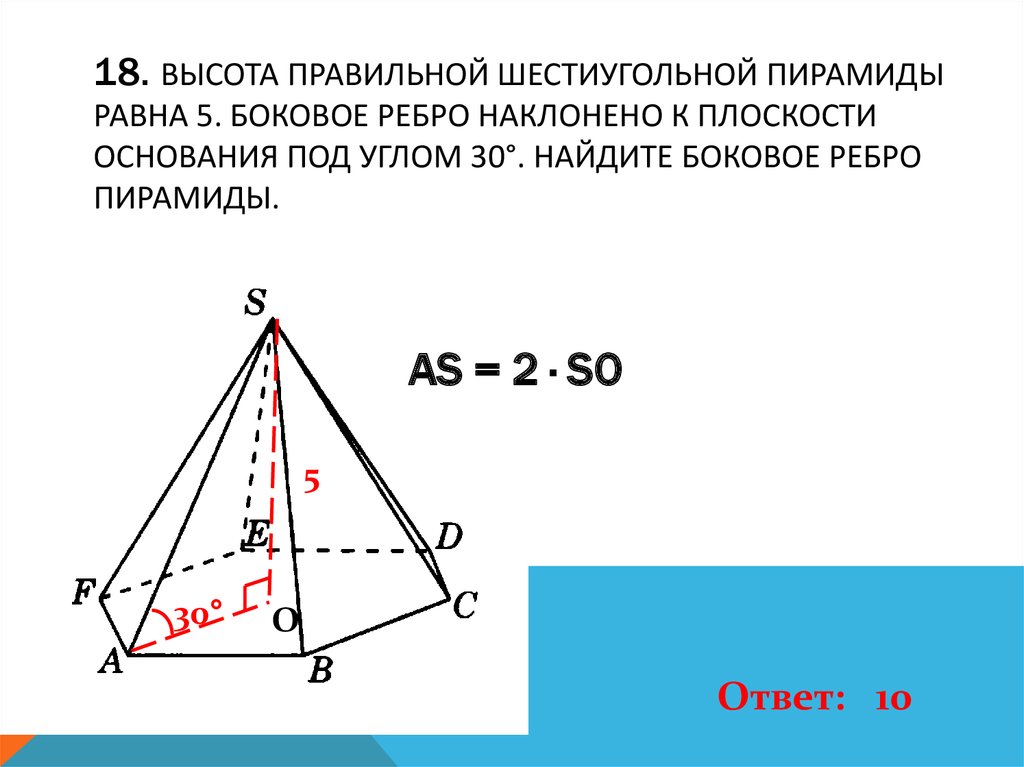
19. 18. Высота правильной шестиугольной пирамиды равна 5. Боковое ребро наклонено к плоскости основания под углом 30°. Найдите

18. ВЫСОТА ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПИРАМИДЫ
РАВНА 5. БОКОВОЕ РЕБРО НАКЛОНЕНО К ПЛОСКОСТИ
ОСНОВАНИЯ ПОД УГЛОМ 30°. НАЙДИТЕ БОКОВОЕ РЕБРО
ПИРАМИДЫ.
AS = 2 · SO
5
30°
О
Ответ: 10

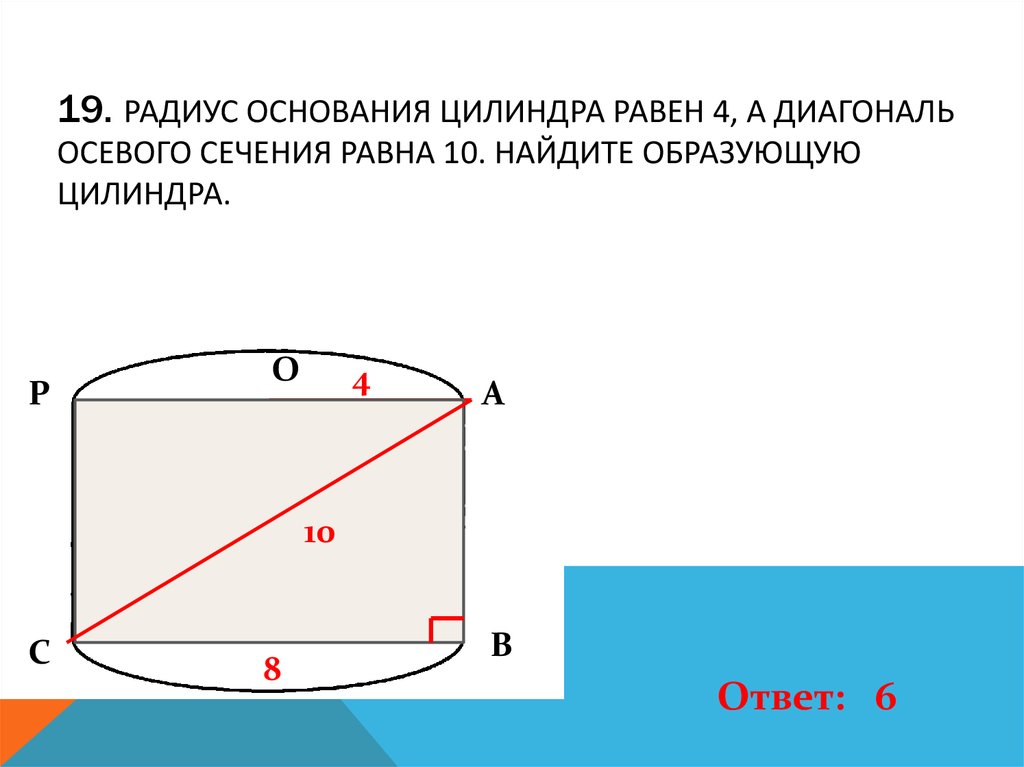
20. 19. Радиус основания цилиндра равен 4, а диагональ осевого сечения равна 10. Найдите образующую цилиндра.

19. РАДИУС ОСНОВАНИЯ ЦИЛИНДРА РАВЕН 4, А ДИАГОНАЛЬ
ОСЕВОГО СЕЧЕНИЯ РАВНА 10. НАЙДИТЕ ОБРАЗУЮЩУЮ
ЦИЛИНДРА.
Р
О
4
А
10
С
8
В
Ответ: 6

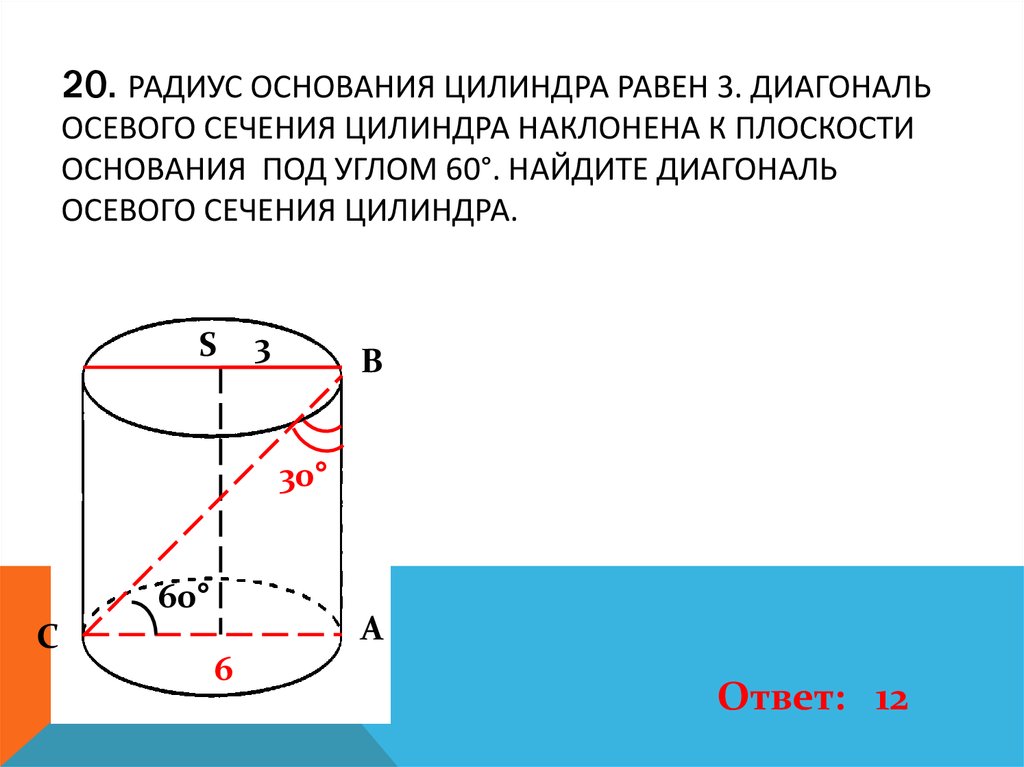
21. 20. Радиус основания цилиндра равен 3. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60°.

20. РАДИУС ОСНОВАНИЯ ЦИЛИНДРА РАВЕН 3. ДИАГОНАЛЬ
ОСЕВОГО СЕЧЕНИЯ ЦИЛИНДРА НАКЛОНЕНА К ПЛОСКОСТИ
ОСНОВАНИЯ ПОД УГЛОМ 60°. НАЙДИТЕ ДИАГОНАЛЬ
ОСЕВОГО СЕЧЕНИЯ ЦИЛИНДРА.
S
3
В
30°
60°
С
А
6
Ответ: 12

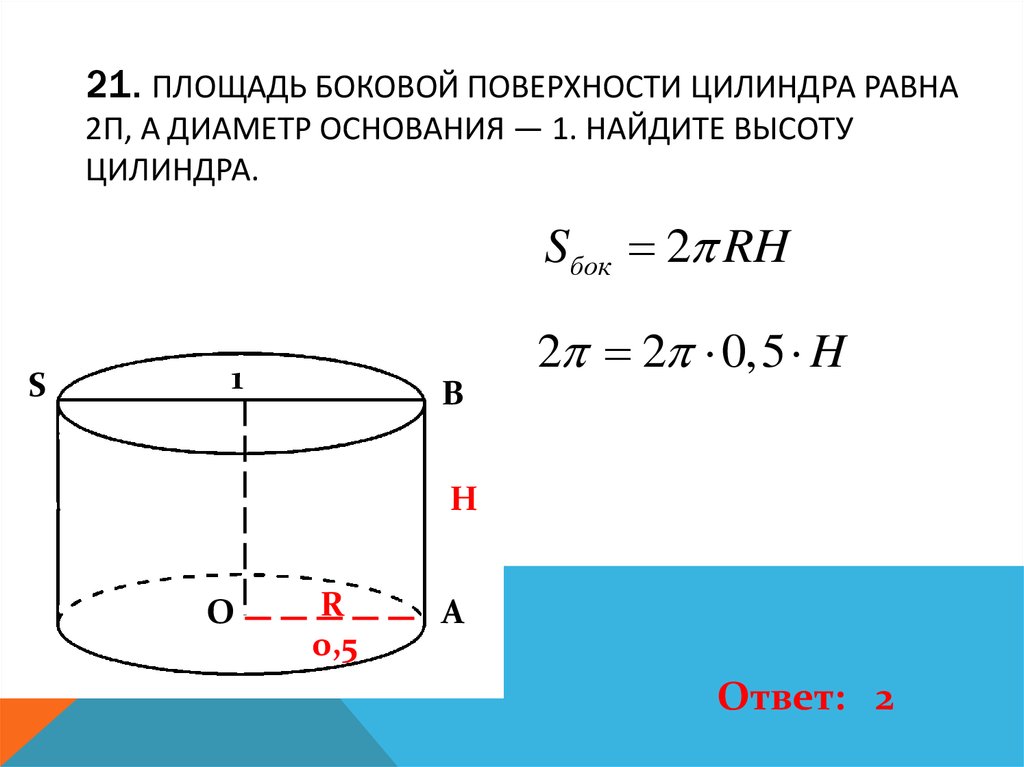
22. 21. Площадь боковой поверхности цилиндра равна 2π, а диаметр основания — 1. Найдите высоту цилиндра.

21. ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ЦИЛИНДРА РАВНА
2Π, А ДИАМЕТР ОСНОВАНИЯ — 1. НАЙДИТЕ ВЫСОТУ
ЦИЛИНДРА.
Sбок 2 RH
S
2 2 0,5 H
1
В
H
О
R
0,5
А
Ответ: 2

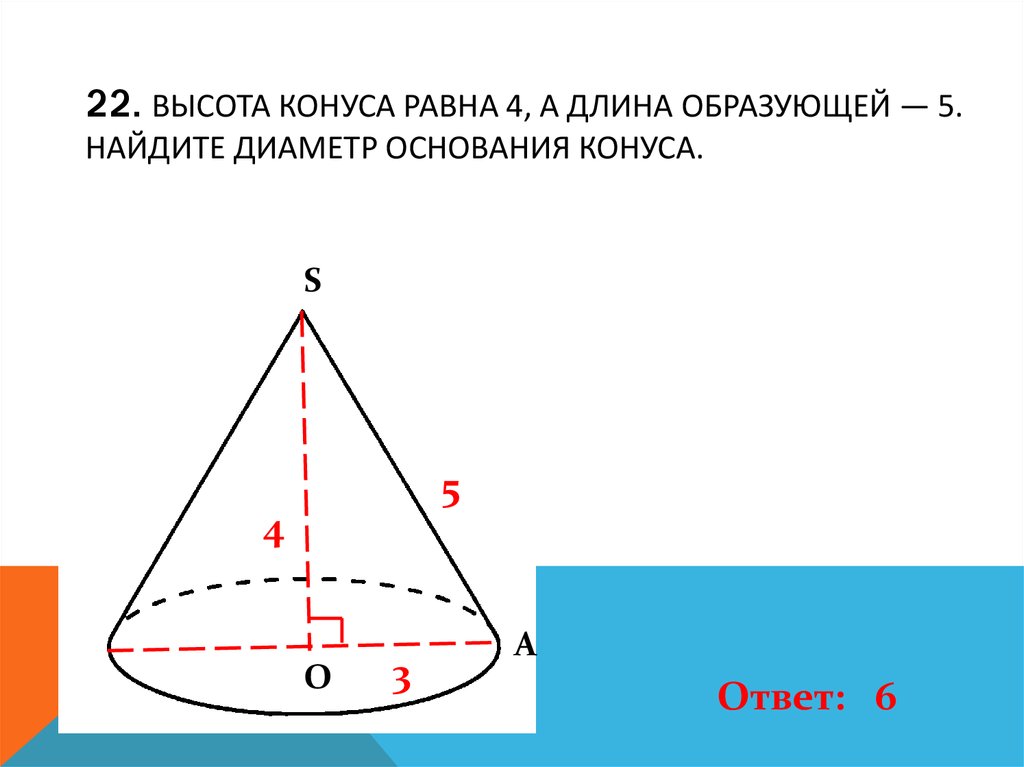
23. 22. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.

22. ВЫСОТА КОНУСА РАВНА 4, А ДЛИНА ОБРАЗУЮЩЕЙ — 5.
НАЙДИТЕ ДИАМЕТР ОСНОВАНИЯ КОНУСА.
S
5
4
O
3
A
Ответ: 6

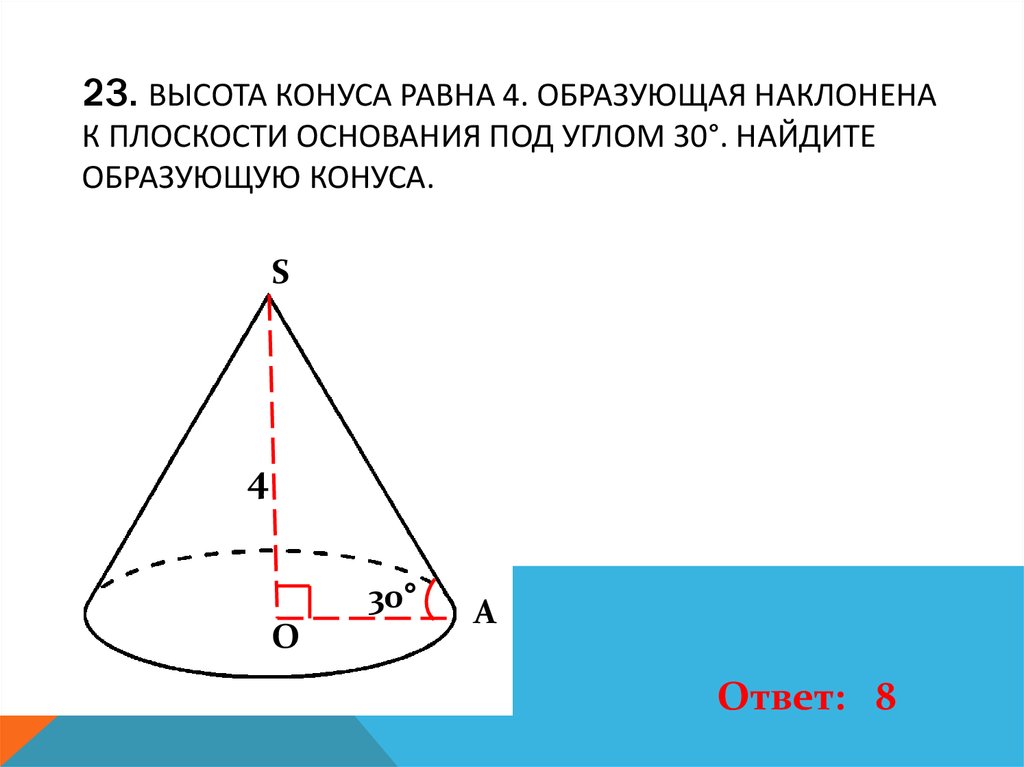
24. 23. Высота конуса равна 4. Образующая наклонена к плоскости основания под углом 30°. Найдите образующую конуса.

23. ВЫСОТА КОНУСА РАВНА 4. ОБРАЗУЮЩАЯ НАКЛОНЕНА
К ПЛОСКОСТИ ОСНОВАНИЯ ПОД УГЛОМ 30°. НАЙДИТЕ
ОБРАЗУЮЩУЮ КОНУСА.
S
4
30°
О
А
Ответ: 8

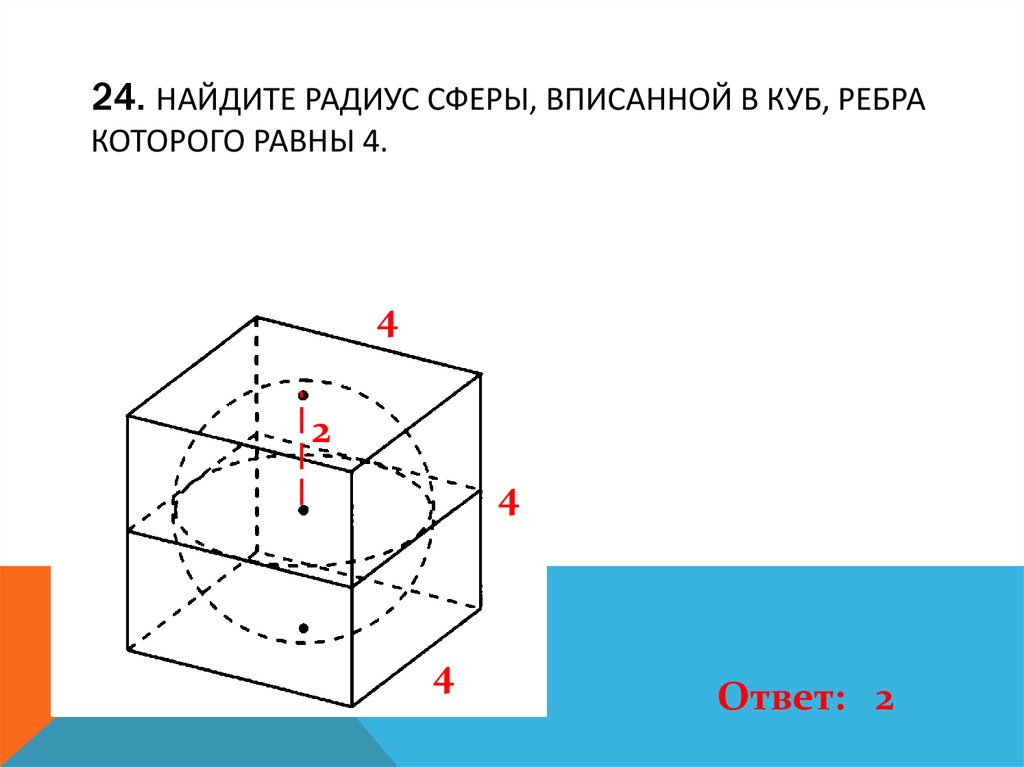
25. 24. Найдите радиус сферы, вписанной в куб, ребра которого равны 4.

24. НАЙДИТЕ РАДИУС СФЕРЫ, ВПИСАННОЙ В КУБ, РЕБРА
КОТОРОГО РАВНЫ 4.
4
2
4
4
Ответ: 2

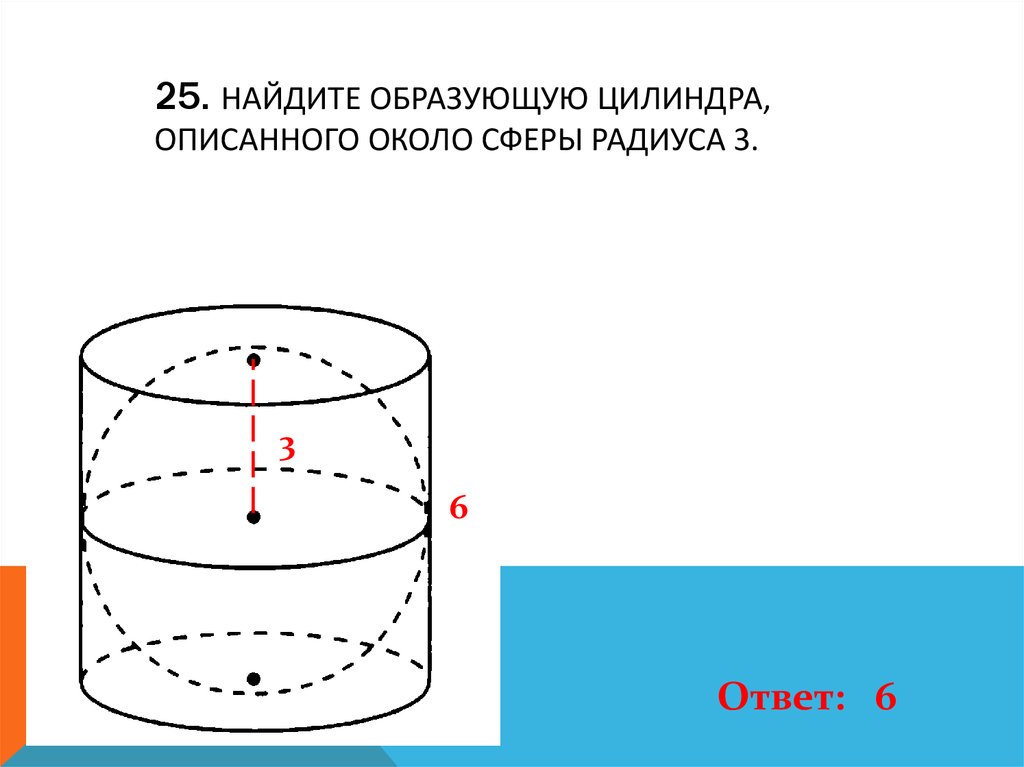
26. 25. Найдите образующую цилиндра, описанного около сферы радиуса 3.

25. НАЙДИТЕ ОБРАЗУЮЩУЮ ЦИЛИНДРА,
ОПИСАННОГО ОКОЛО СФЕРЫ РАДИУСА 3.
3
6
Ответ: 6

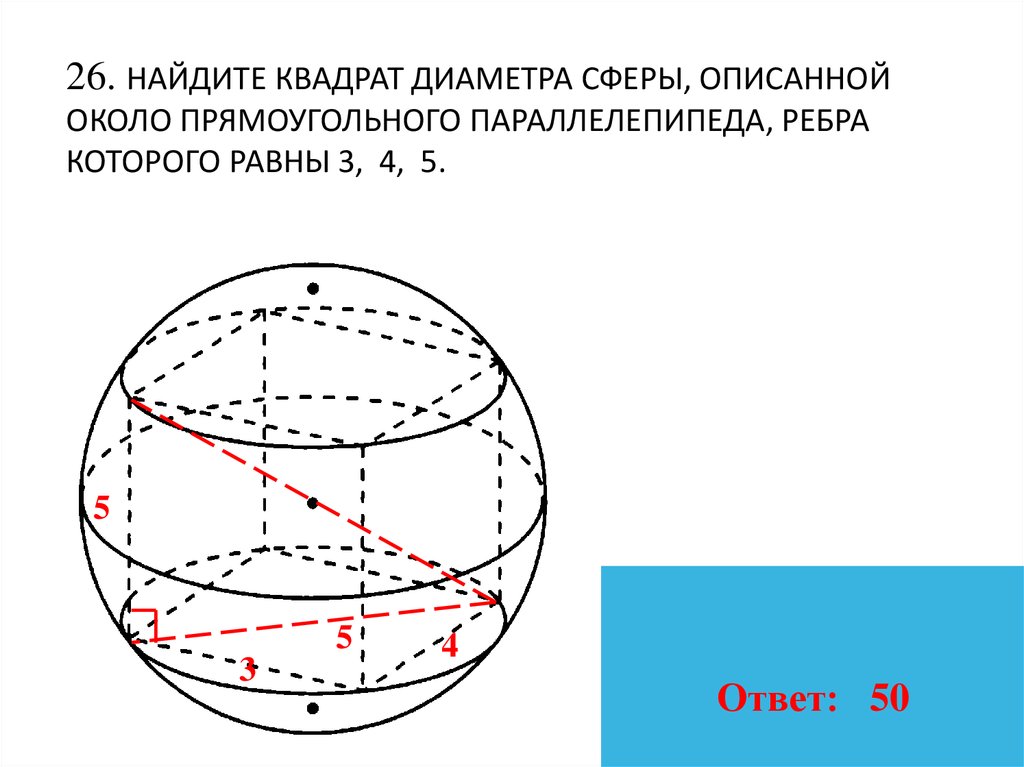
27. 26. Найдите квадрат диаметра сферы, описанной около прямоугольного параллелепипеда, ребра которого равны 3, 4, 5.

26. НАЙДИТЕ КВАДРАТ ДИАМЕТРА СФЕРЫ, ОПИСАННОЙ
ОКОЛО ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА, РЕБРА
КОТОРОГО РАВНЫ 3, 4, 5.
5
5
3
4
Ответ: 50