Свойства равнобедренного треугольника

1. Треугольник

Образовательные – повторение, обобщение и проверка усвоения знаний по
теме «Медианы, биссектрисы и высоты треугольника»; знакомство со
свойствами равнобедренного треугольника; выработка основных навыков.
Развивающие – развивать внимание учащихся, усидчивость, настойчивость,
логическое мышление, математическую речь;
Воспитательные – посредством урока воспитывать внимательное
отношение друг к другу, прививать умение слушать товарищей,
взаимовыручку, самостоятельность.

2.

3.

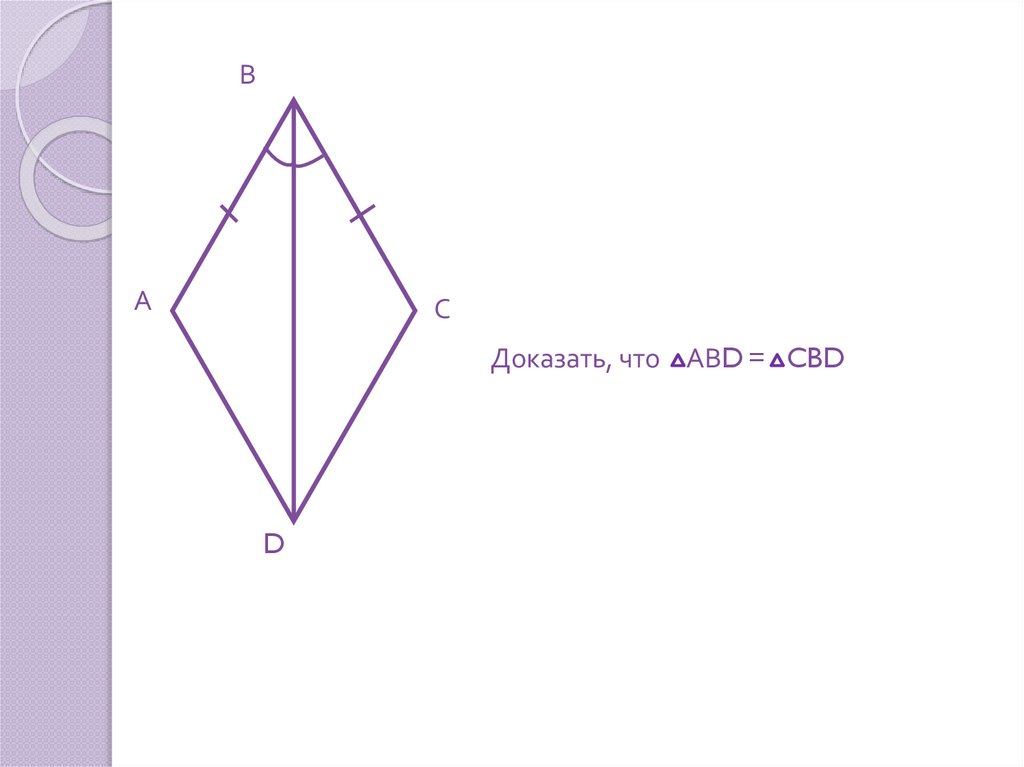
В
А
С
Доказать, что АВD = CBD
D

4.

B
Дано: BM – высота
Доказать,
что
A
M
C
ABM =
ВСM
АВС

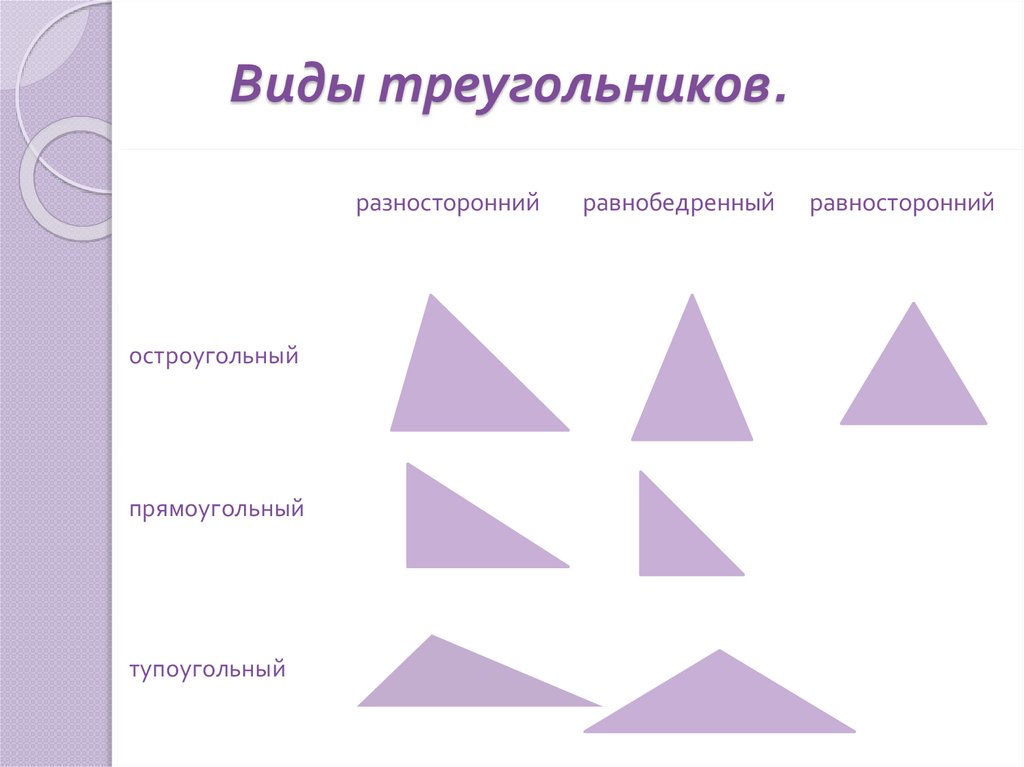
5. Виды треугольников.

разносторонний
остроугольный
прямоугольный
тупоугольный
равнобедренный
равносторонний

6. Равнобедренный треугольник

Треугольник называется
равнобедренным,
если две его стороны равны

7.

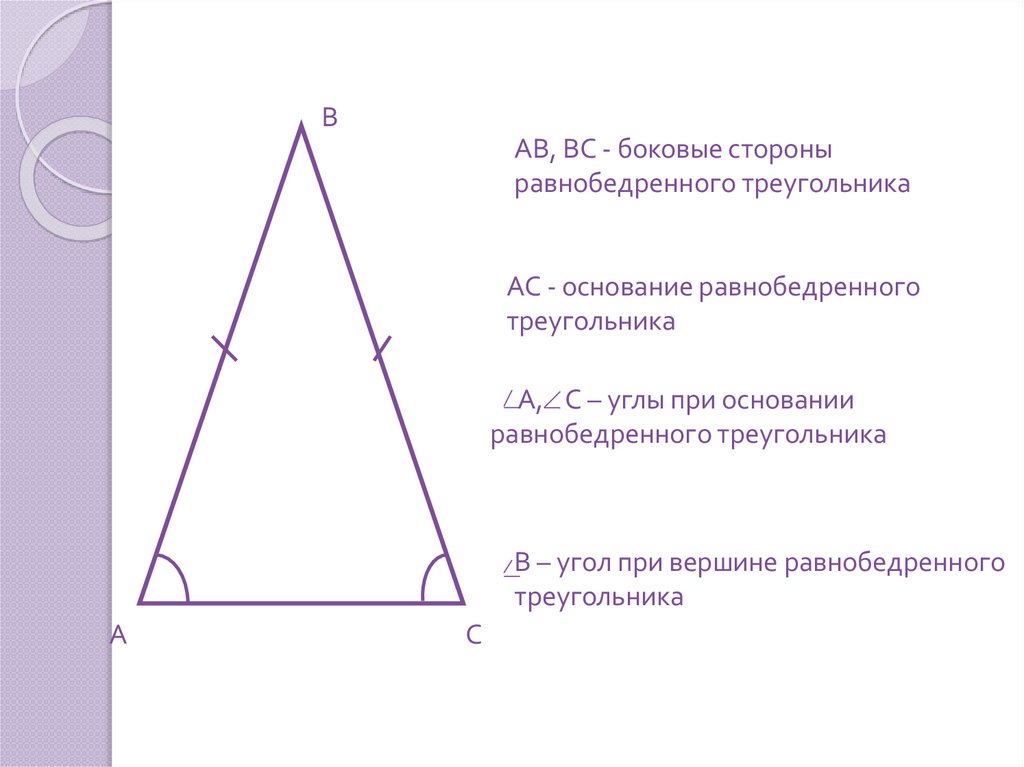
В
АВ, ВС - боковые стороны
равнобедренного треугольника
АС - основание равнобедренного
треугольника
А, С – углы при основании
равнобедренного треугольника
В – угол при вершине равнобедренного
треугольника
А
С

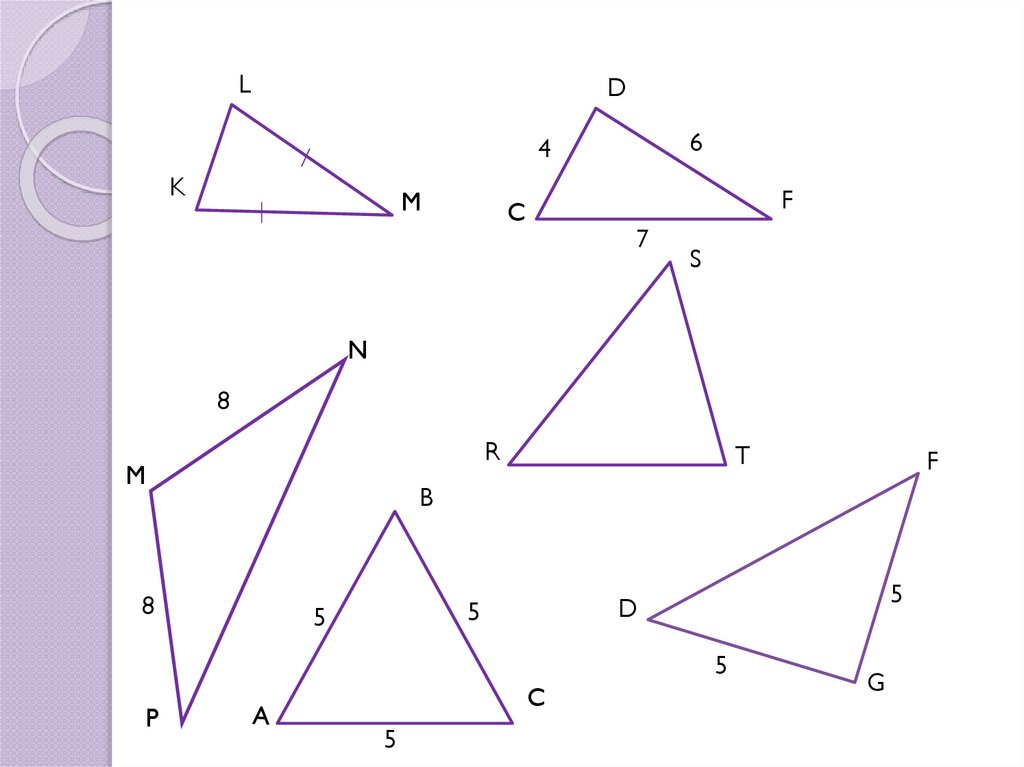
8.

L
D
6
4
K
M
F
C
7
S
N
8
R
M
8
T
B
5
5
D
5
5
P
F
C
5
G

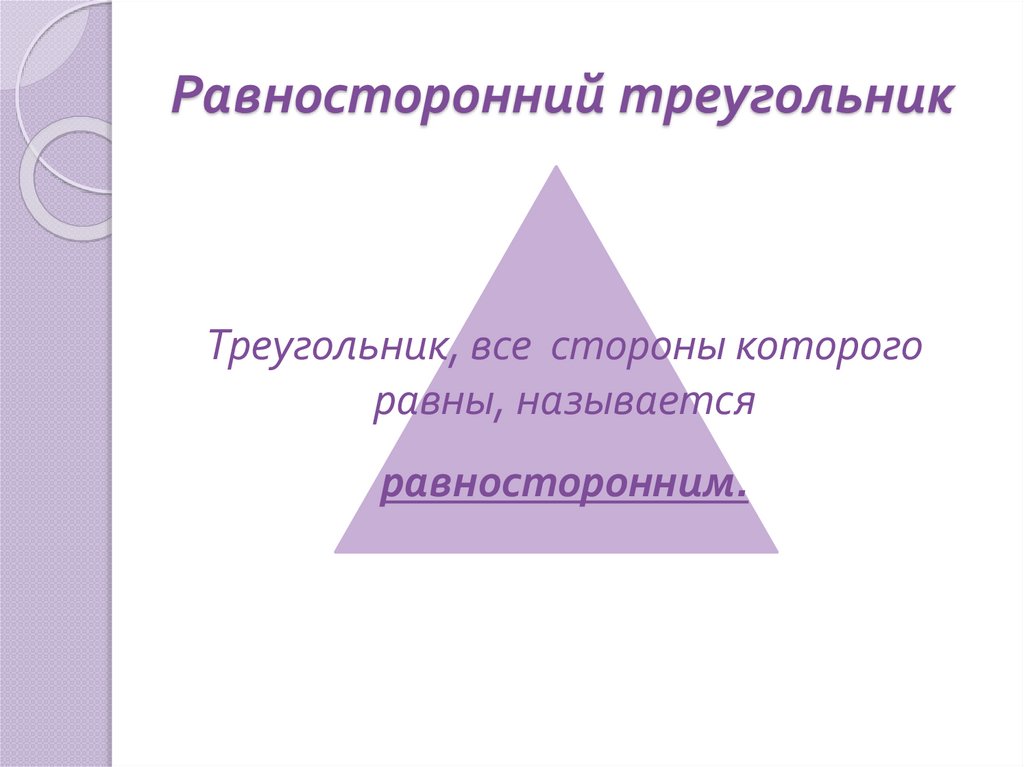
9. Равносторонний треугольник

Треугольник, все стороны которого
равны, называется
равносторонним.

10.

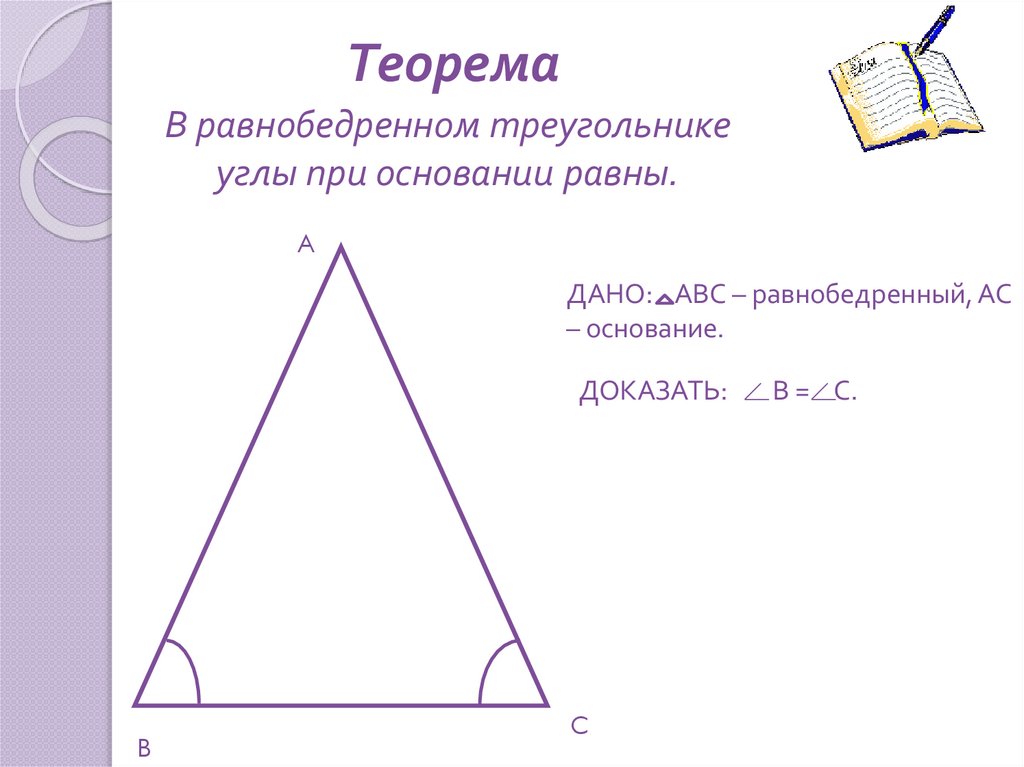
Теорема
В равнобедренном треугольнике
углы при основании равны.
A
ДАНО: АВС – равнобедренный, АС
– основание.
ДОКАЗАТЬ:
B
C
В = С.

11.

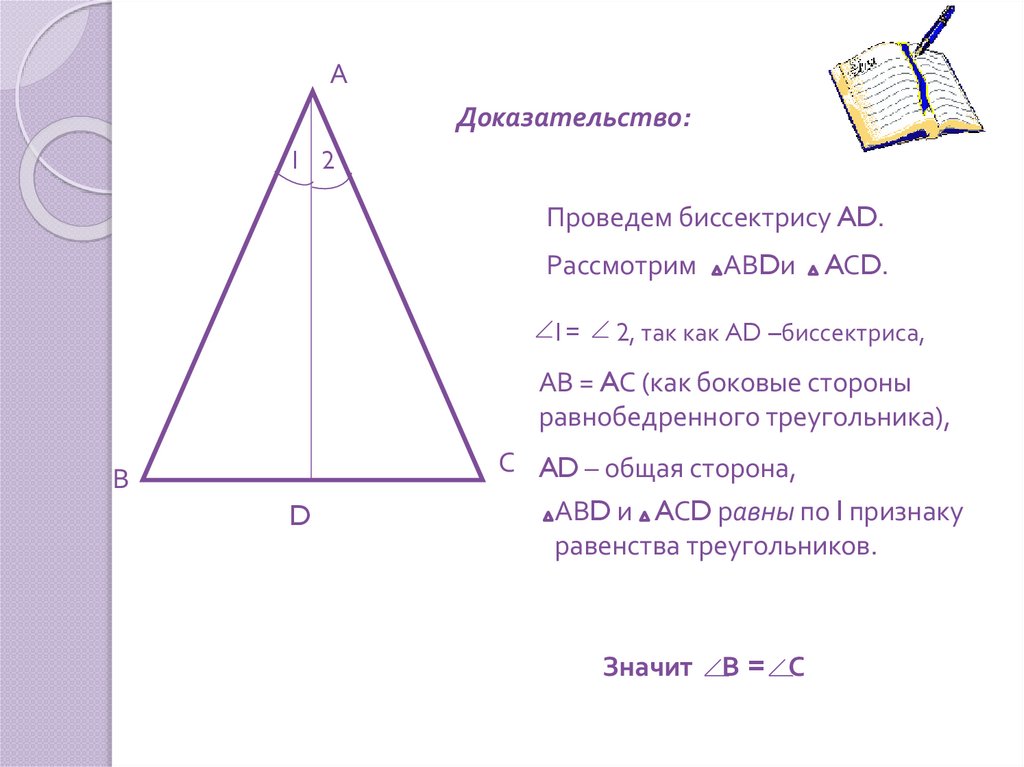
А
Доказательство:
1 2
Проведем биссектрису AD.
Рассмотрим АВDи AСD.
1=
2, так как AD –биссектриса,
АВ = AС (как боковые стороны
равнобедренного треугольника),
С AD – общая сторона,
В
D
АВD и AСD равны по I признаку
равенства треугольников.
Значит
В= С

12. Практическая работа

I.
II.
III.
IV.
V.
VI.
Начертите равнобедренный треугольник
АВС с основанием ВС.
С помощью транспортира и линейки
проведите биссектрису из вершины А к
основанию ВС.
С помощью чертежного угольника
проведите высоту из вершины А.
С помощью масштабной линейки
проведите медиану из вершины А.
Что вы заметили? Что вас удивило?
Попробуйте высказать гипотезу.

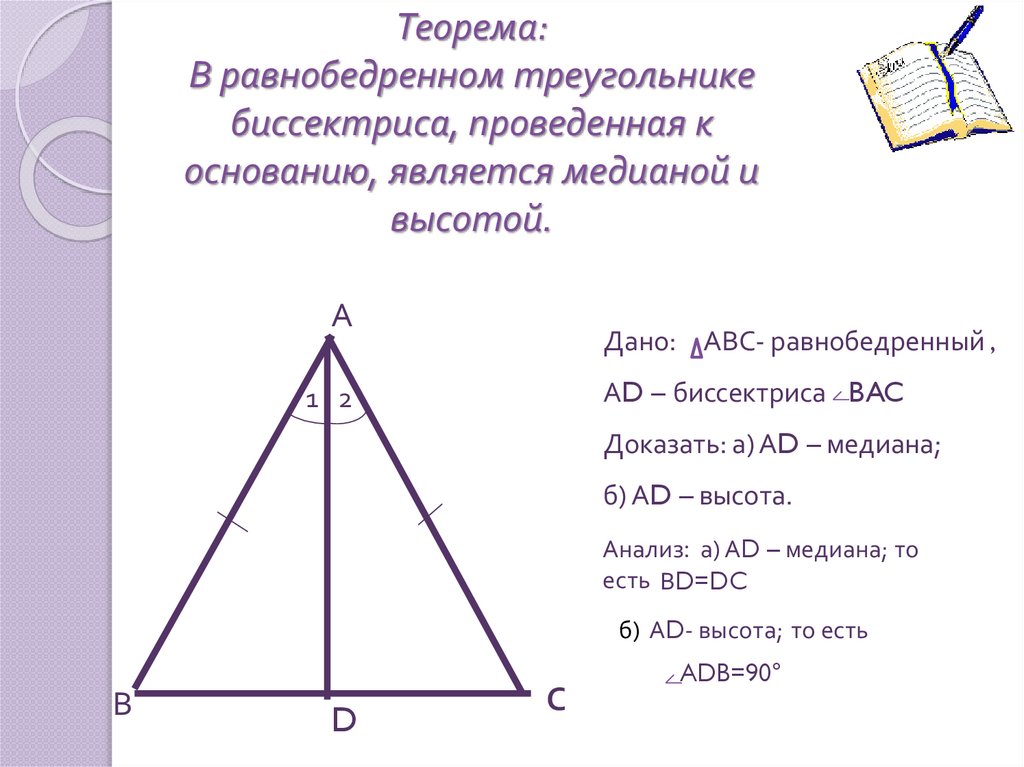
13. Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

А
Дано: АВС- равнобедренный ,
АD – биссектриса BAC
1 2
Доказать: а) АD – медиана;
б) АD – высота.
Анализ: а) АD – медиана; то
есть ВD=DC
б) АD- высота; то есть
В
D
С
ADB=90°

14.

Доказательство
А
∆ ABD = ∆ ACD (СУС) (АD – общая
сторона, АВ = АС и 1 = 2, так как
AD-биссектриса).
2
1
Из равенства треугольников
следует, что ВD = DC и 3 = 4.
Если ВD = DC, то D – середина
стороны ВС, тогда АD – медиана.
3
В
Так как 3 и 4 смежные и равны
друг другу, то они прямые. Значит
отрезок AD – высота.
4
D
С
Всегда ли верно утверждение: «Биссектриса равнобедренного
треугольника является одновременно его медианой и высотой» ?

15. Физкультминутка

Раз-подняться, подтянуться.
Два-согнутся, разогнуться,
Три-в ладошки три хлопка,
Головою три кивка.
На четыре-руки шире.
Пять- руками помахать
Шесть- на место тихо сесть.

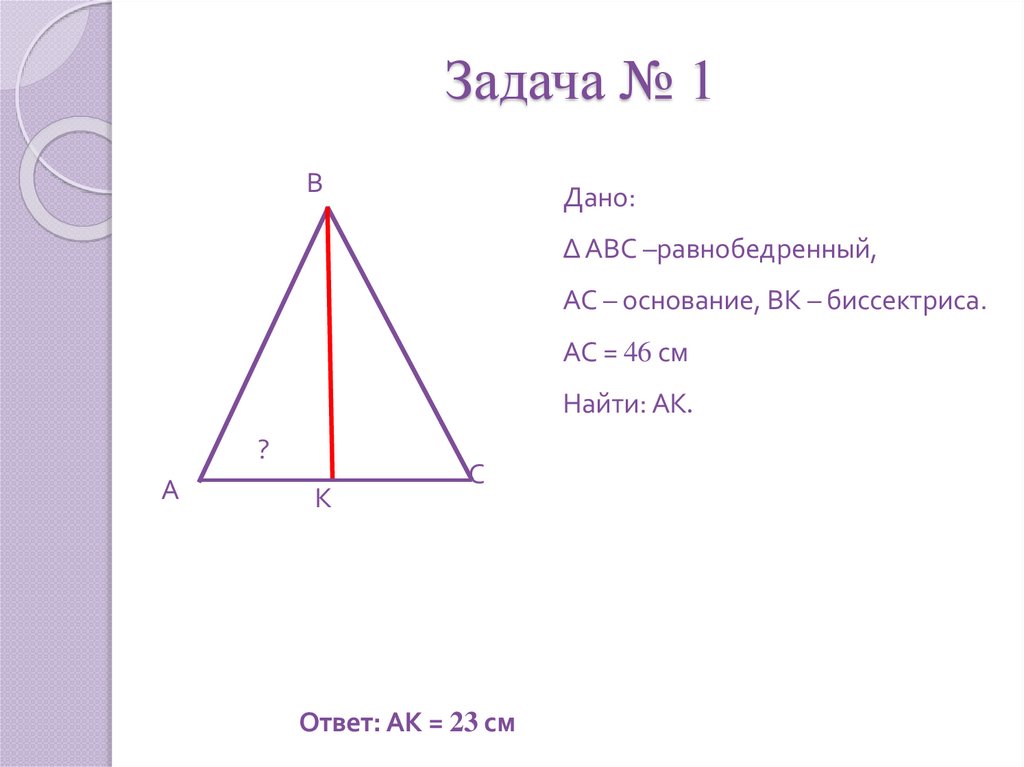
16. Задача № 1

В
Дано:
∆ АВС –равнобедренный,
АС – основание, ВК – биссектриса.
АС = 46 см
Найти: АК.
?
А
К
С
Ответ: АК = 23 см

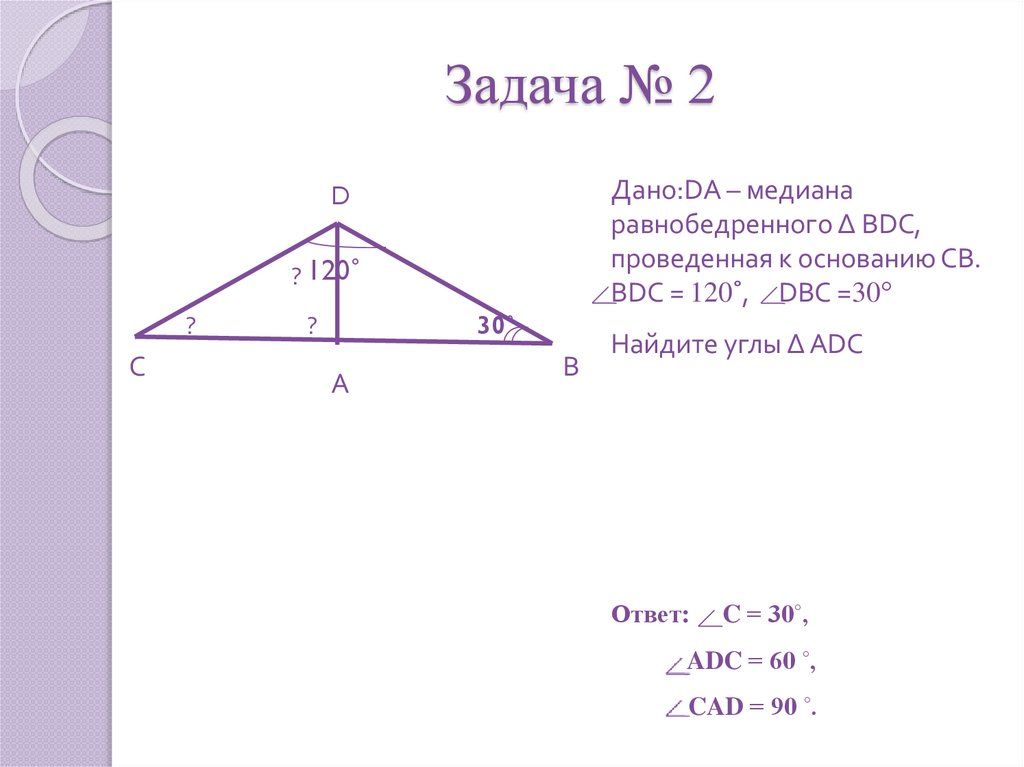
17. Задача № 2

Дано:DA – медиана
равнобедренного ∆ ВDС,
проведенная к основанию СВ.
BDC = 120˚, DBC =30°
D
? 120˚
?
С
30˚
?
А
В
Найдите углы ∆ АDС
Ответ:
C = 30˚,
ADC = 60 ˚,
CAD = 90 ˚.

18.

№108
A
Дано: ∆ АВС равнобедренный
АВ=АС, Р∆ АВС= 40 см
∆ BCD- равносторонний
Р∆ ВСD= 45 см.
Найти: АВ, ВС.
D
B
C
Решение: ∆ BCD- равносторонний треугольник, то есть
ВС=СD=ВD , Р∆ ВСD= 45 см=3ВС, отсюда ВС=45:3=15(см).
По условию Р∆ АВС= 40 см, ВС=15см, тогда АВ+АС=4015=25(см). Так, по условию ∆ АВС - равнобедренный, то
АВ=АС=25:2=12,5(см).
Ответ: АВ=12,5см; ВС=15см.

19. Задание на дом:

п.18,№104,107, 117

20.

"На сегодняшнем уроке я понял, я узнал, я разобрался…";
"Я похвалил бы себя…";
"Особенно мне понравилось…";
"После урока мне захотелось…";
"Я мечтаю о …";
"Сегодня мне удалось…";
"Я сумел…";
"Было интересно…";
"Было трудно…";
"Я понял, что…";
"Теперь я могу…";
"Я почувствовал, что…";
"Я научился…";

21. Где в жизни встречаются равнобедренные треугольники?