Похожие презентации:
«Уравнение плоскости» (профильный уровень), урок №1, 11 класс
1. Методическая разработка урока геометрии в 11 классе по теме «Уравнение плоскости» (профильный уровень) урок №1.
Автор разработки:Малинская Елена Геннадьевна
учитель математики
МАОУ гимназии № 40 имени Ю. А. Гагарина
г. Калининград, 2015 г.
2. Этапы решения задач методом координат
• 1. Выбор системы координат в пространстве• 2. Нахождение координат необходимых точек и
векторов, или уравнения плоскостей, кривых и
фигур
• 3. Решение примера, используя ключевые задачи
или формулы данного метода
• 4. Переход от аналитических соотношений к
метрическим.
19.03.2019
2
3. Цели:
• Ввести понятия общего уравнения плоскости,матрицы и определителя.
• Изучить алгоритм нахождения определителя
квадратных матриц второго и третьего
порядков.
• Выработать умение записывать уравнение
плоскости, проходящей через три различные
точки.
19.03.2019
3
4. Общее уравнение плоскости
Если в пространстве фиксирована произвольная декартовасистема координат Oxyz, то всякое уравнение первой степени с
тремя переменными x y z определяет относительно этой системы
плоскость.
Ax By Cz D 0 (1)
A; B; C; D – некоторые постоянные, причем из чисел A; B; C хотя
бы одно отлично от нуля.
Общее уравнение плоскости
Общее уравнение плоскости называется полным, если все
коэффициенты А; B; C; D отличны от нуля.
В противном случае уравнение называется неполным.
5. Виды неполных уравнений
2)D 0;
A 0;
Ax By Cz 0 Плоскость проходит через точку О.
By Cz D 0 ll (OX )
z
3)
B 0;
Ax Cz D 0
4)
C 0;
Ax By D 0 ll (OZ )
1)
ll (OY )
6)
A 0; B 0 Cz D 0 ll ( XOY )
B 0; C 0 Ax D 0 ll (YOZ )
7)
A 0; C 0
5)
8)
9)
10)
By D 0 ll ( XOZ )
B 0; C 0; D 0 Ax 0 x 0
A 0; C 0; D 0
A 0; B 0; D 0
By 0 y 0
Cz 0 z 0
0
x
(YOZ )
( XOZ )
( XOY )
y
6. Алгоритм составления уравнения плоскости, проходящей через три точки
М(x¹,y¹,z¹), N(x²,y²,z²), K(x³,y³,z³)• Подставить координаты точек в уравнение плоскости
Ax By Cz D 0
Получится система трех уравнений с четырьмя переменными
Решить систему уравнений и найти А; В; С
Подставить найденные значения А, В и С в общее уравнение
плоскости
Замечание :
Если плоскость проходит через начало координат, положить D = 0,
если не проходит, то D = 1
7. Упражнение №1
Напишите уравнение плоскости, проходящей через точки:а) A (1,0,0), B (0,1,0) и C (0,0,1); б) M(3,-1,2), N(4,1,-1) и K(2,0,1).
Решение:
Подставим координаты точек в уравнение плоскости
Ax By Cz D 0
а)
Ответ: а) x+y+z–1=0;
б)
б) x+4y+3z-5=0.
8. Метод Гаусса
Метод Гаусса — классический метод решения системы линейныхалгебраических уравнений. Это метод последовательного исключения
переменных, когда с помощью элементарных преобразований система
уравнений приводится к равносильной системе ступенчатого (или
треугольного) вида, из которого последовательно, начиная с последних (по
номеру) переменных, находятся все остальные переменные.
Система т линейных уравнений с п неизвестными имеет вид:
a11 x1 a12 x2 ... a1n xn b1
a21 x1 a22 x2 ... a2 n xn b2
...............................................
am1 x1 am 2 x2 ... am n xn bn
x1 , x2, …, xn – неизвестные.
ai j - коэффициенты при неизвестных.
bi - свободные члены (или правые части)
9. Уравнение плоскости, проходящей через три точки (способ №2)
Пусть точки М1(х1 ; у1 ; z1 ), М2(х2 ; у2 ; z2 ) и М3(х3 ; у3 ; z3 )не лежат на одной прямой.
М3
М1
x x1
y y1
z z1
x 2 x1
y 2 y1
z2 z1 0
x 3 x1
y 3 y1
z3 z1
М
М2
Уравнение плоскости,
проходящей через 3 точки
10.
МатрицыМатрицей размера m n называется совокупность mn чисел,
расположенных в виде таблицы из m строк и n столбцов:
a11 a12 ... a1n
Пример:
a
a22 ... a2 n
21
.
A
.
.
.
.
a
a
...
a
mn
m1 m 2
2 1 4
A 6 2 8
0 3 6
размера 3 3
Числа, составляющие матрицу, называются элементами
матрицы. Если m≠n, то матрица называется прямоугольной.
Если m=n, то матрица называется квадратной порядка n.
11.
Диагонали матрицыa1
a Матрица размера m 1 вида состоит из одного столбца и
2 называется вектор-столбцом, а матрица A=[a1 a2…an]
размера 1 n, состоящая из одной строки –
a m вектор-строкой.
В случае квадратной матрицы
элементы a11, a22,…ann
a11 a12 ... a1n
a
a
...
a
22
2n
A 21
.
.
.
.
an1 an 2 ... ann
образуют главную диагональ, а
элементы an1, an-1 2,…a1n – побочную диагональ матрицы.
12.
ОпределителиПонятие определителя вводится только для квадратных матриц.
Определителем n-го порядка матрицы А называется алгебраическая
сумма всевозможных произведений элементов, взятых точно по одному из
каждой строки и каждого столбца матрицы А. Знак каждого слагаемого
определяется специальным правилом.
Определители n-го порядка содержат n! членов.
A
a11
a12
a 21
a 22
= a11a22- a12a21 –
Пример:
A
2 5
3
7
определитель второго порядка.
2 7 ( 5) 3 14 ( 15) 29.
13.
определитель третьего порядка.a11
a12
a13
A a 21
a 22
a31
a32
a 23 a11a22a33+a12a23a31+ a13a21a32- a13a22a31-a11a23a32- a12a21a33
a33
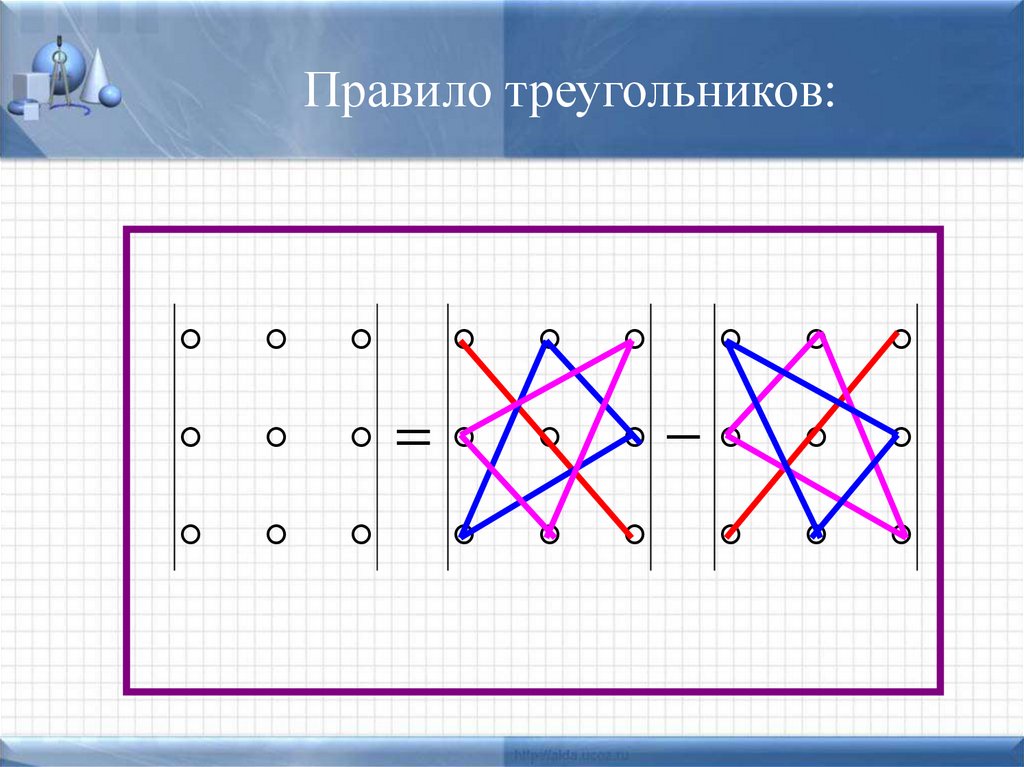
Правило треугольника: три положительных члена определителя третьего
порядка представляют собой произведения элементов главной диагонали и
элементов, находящихся в вершинах двух равнобедренных треугольников,
основания которых параллельны главной диагонали. Три его отрицательных
члена представляют собой произведения элементов побочной диагонали и
элементов, находящихся в вершинах двух равнобедренных треугольников,
основания которых параллельны побочной диагонали.
«+»
«-»
14.
Правило треугольников:15.
Вычислить определители матриц1 2
A
3 5
1 1 1
B 2 1 1
1 1 2
16.
Решение:A
1
2
3 5
1 5 ( 3) 2 11
1 1 1
B 2
1
1
1
1
2
1 1 2 ( 1) 1 1 1 2 1 1 1 1 ( 1) 2 2 1 1 1 5
17. Упражнение №2
Напишите уравнение плоскости, проходящей через точки:а) A (1,0,0), B (0,1,0) и C (0,0,1); б) M(3,-1,2), N(4,1,-1) и K(2,0,1).
Решение:
Подставим координаты точек
в уравнение плоскости
а)
x x1
y y1
z z1
x 2 x1
y 2 y1
z2 z1 0
x 3 x1
y 3 y1
z3 z1
б)
=0
=0
=0
=0
Ответ: а) x+y+z–1=0;
б) x+4y+3z-5=0.
18. Домашнее задание
• Повторить координаты основныхпространственных фигур
• Выучить теоретический материал по данной теме
• Решить задачи № 3(б) (приложение № 1)
• Создать в программе
• « Microsoft Publisher» буклет- справочник по
данной теме (необязательное задание)
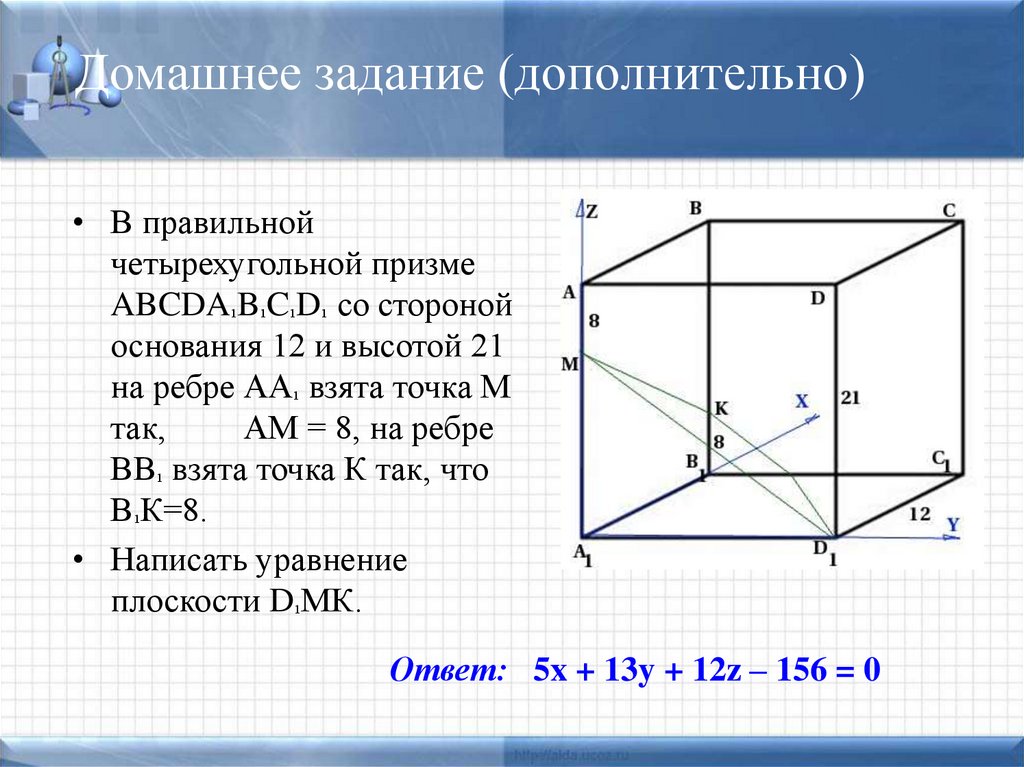
19. Домашнее задание (дополнительно)
• В правильнойчетырехугольной призме
ABCDA¹B¹C¹D¹ со стороной
основания 12 и высотой 21
на ребре АА¹ взята точка М
так,
АМ = 8, на ребре
ВВ¹ взята точка К так, что
В¹К=8.
• Написать уравнение
плоскости D¹МК.
Ответ: 5x + 13y + 12z – 156 = 0

















 Математика
Математика








