Похожие презентации:
Теорема Пифагора. Египетский треугольник
1.
8 класс2.
Пифагор Самосский (ок.580 — ок. 500 до н. э.) —
древнегреческий философ,
религиозный и политический
деятель, основатель
пифагореизма, математик.
Пифагору приписывается
изучение свойств целых
чисел и пропорций,
доказательство теоремы
Пифагора и др.
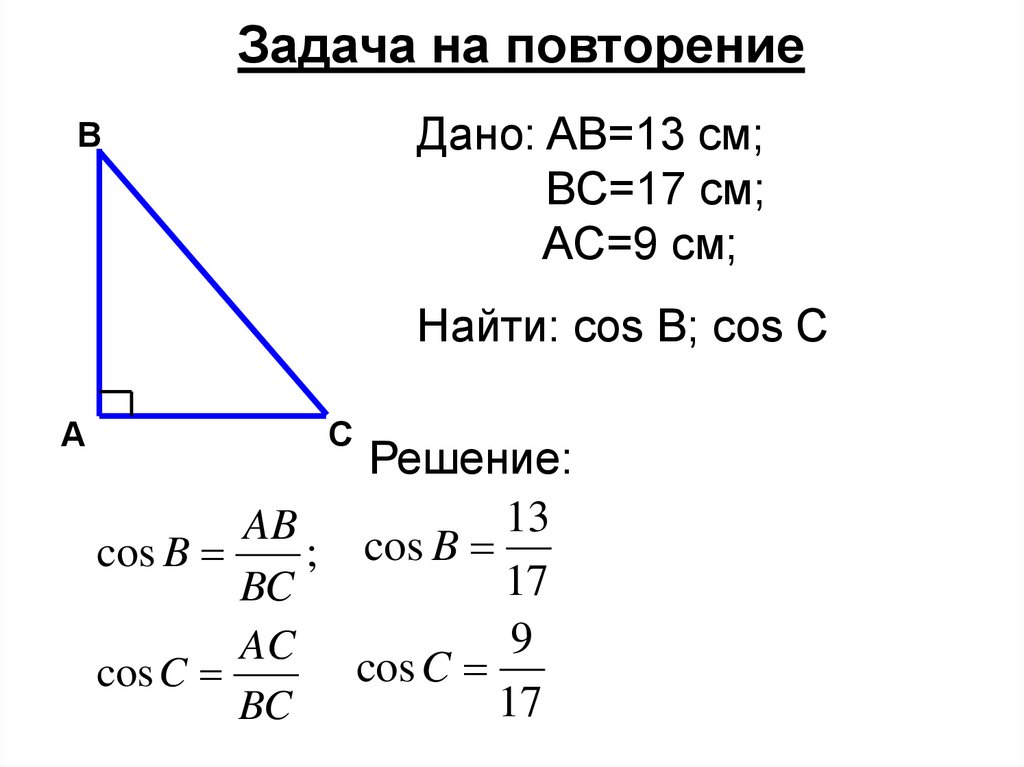
3. Задача на повторение
Дано: AB=13 см;BC=17 см;
AC=9 см;
B
Найти: cos B; cos C
A
C
Решение:
13
AB
cos B
; cos B
17
BC
9
AC
cos C
cos C
17
BC
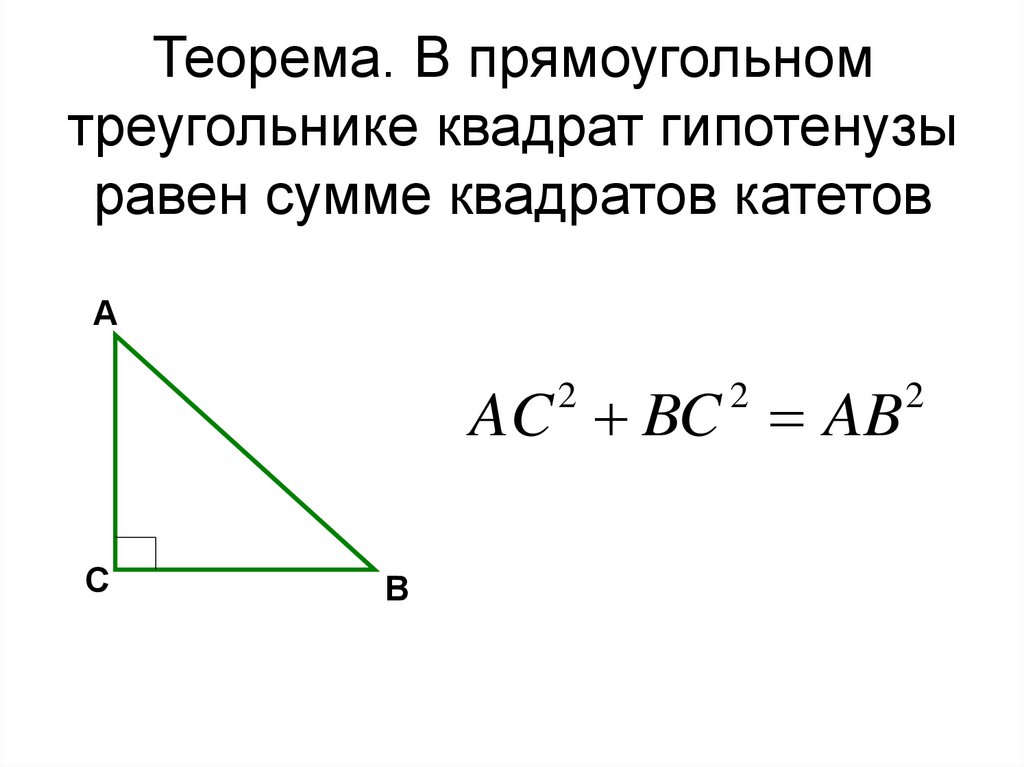
4. Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
AAC BC AB
2
С
B
2
2
5. Доказательство:
Acos A
AD
из ADC
AC
AD AC
AC AB
cos B
B
D
cos A
AС
из ABC
AB
AB AD AC 2
BD
из BDC
BC
BD BC
BC AB
C
cos B
BC
из ABC
AB
AB BD BC 2
AB AD AB BD AC 2 BC 2
AB AD BD AC 2 BC 2
AD BD AB
AB AB AC 2 BC 2
AB 2 AC 2 BC 2
Теорема доказана
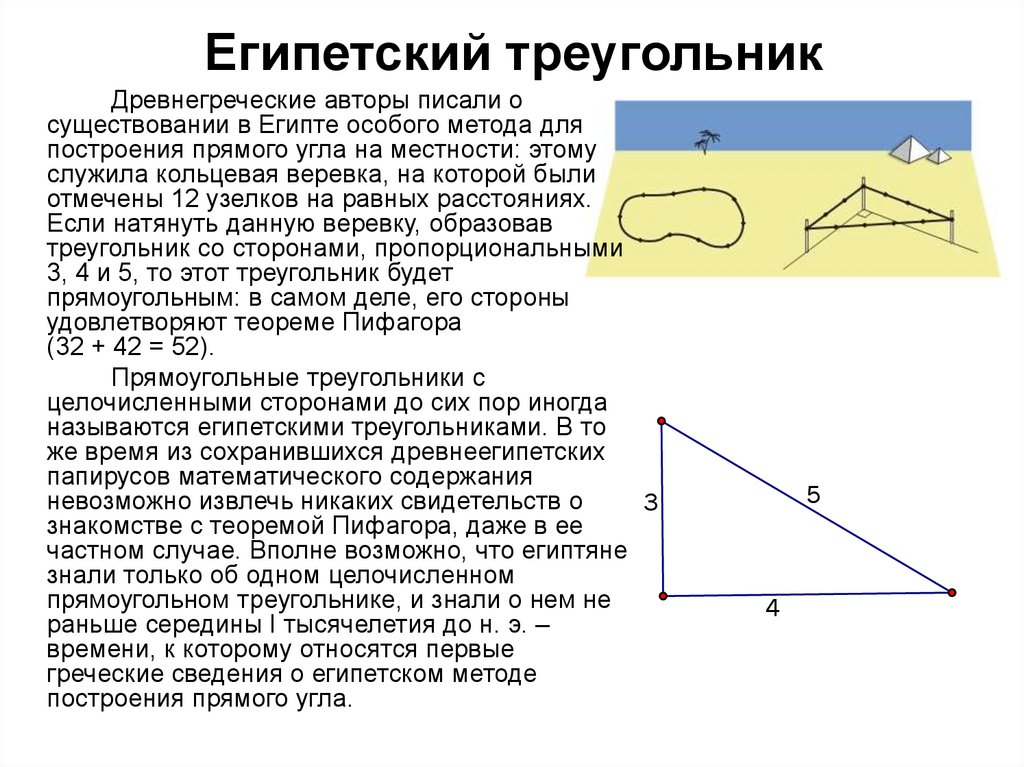
6. Египетский треугольник
Древнегреческие авторы писали осуществовании в Египте особого метода для
построения прямого угла на местности: этому
служила кольцевая веревка, на которой были
отмечены 12 узелков на равных расстояниях.
Если натянуть данную веревку, образовав
треугольник со сторонами, пропорциональными
3, 4 и 5, то этот треугольник будет
прямоугольным: в самом деле, его стороны
удовлетворяют теореме Пифагора
(32 + 42 = 52).
Прямоугольные треугольники с
целочисленными сторонами до сих пор иногда
называются египетскими треугольниками. В то
же время из сохранившихся древнеегипетских
папирусов математического содержания
невозможно извлечь никаких свидетельств о
3
знакомстве с теоремой Пифагора, даже в ее
частном случае. Вполне возможно, что египтяне
знали только об одном целочисленном
прямоугольном треугольнике, и знали о нем не
раньше середины I тысячелетия до н. э. –
времени, к которому относятся первые
греческие сведения о египетском методе
построения прямого угла.
5
4
7.
Задача 1Дано: ΔABC, АВ=6 см,
АС=8 см
В
Найти: BC
?
А
С Решение:
AB AC BC
2
2
2
BC AB 2 AC 2
BC 36 64 100 10см
Ответ :10 см.
8.
Задача 2.Дано: ABC
А
Найти: ВС
5 см
7 см
Решение:
AB 2 BC 2 AC 2
BC AC AB
2
2
2
BC 49 25 24 4 6 2 6см
Ответ : 2 6см.
В
?
С
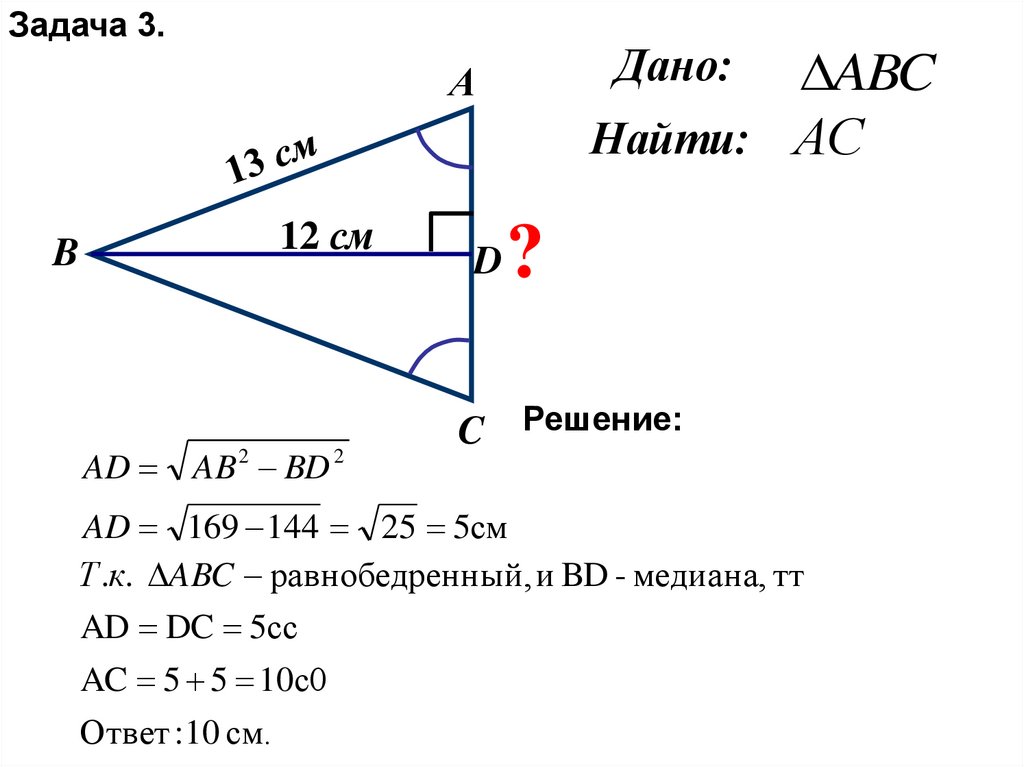
9.
Задача 3.ABC
Найти: АС
Дано:
А
12 см
B
AD AB 2 BD 2
D
?
C Решение:
AD 169 144 25 5см
Т .к. ABC равнобедренный, и BD - медиана, тт
AD DC 5сс
AC 5 5 10с0
Ответ :10 см.
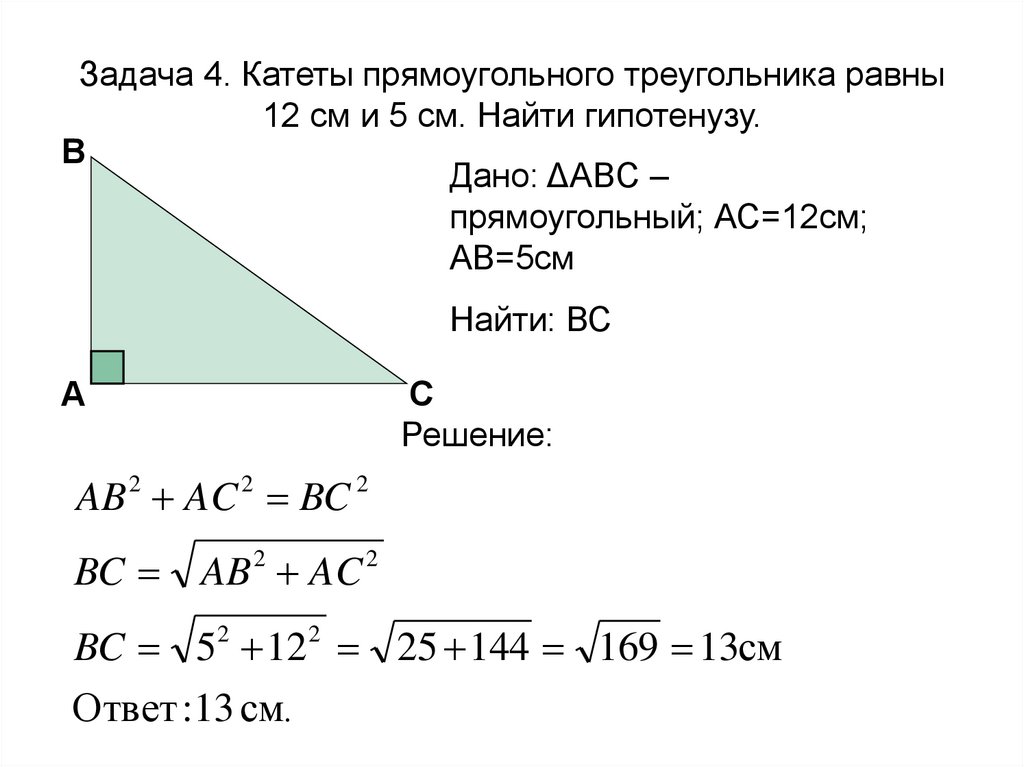
10. Задача 4. Катеты прямоугольного треугольника равны 12 см и 5 см. Найти гипотенузу.
BДано: ΔABC –
прямоугольный; АС=12см;
АВ=5см
Найти: ВС
A
C
Решение:
AB 2 AC 2 BC 2
BC AB 2 AC 2
BC 52 12 2 25 144 169 13см
Ответ :13 см.
11. Задача 5. Диагональ прямоугольника равна 5 см, а одна из его сторон – 3 см. Найти вторую сторону прямоугольника.
BC Дано: ABCD – прямоугольник;
BD=5см; АВ=3см
Найти: AD
A
D
Решение:
AD 2 AB 2 BD 2
AD BD 2 AB 2
AD 25 9 16 4см
Ответ : 4 см.






 Математика
Математика








