Похожие презентации:
Определение прямоугольного треугольника. Теорема Пифагора
1. Определение прямоугольного треугольника
2. Определение прямоугольного треугольника
Треугольник, один из углов которогоравен 90°, называется прямоугольным
3. Теорема Пифагора.
4. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
c a b2
2
2
АВ ВС АС
2
2
2
5. Синус острого угла.
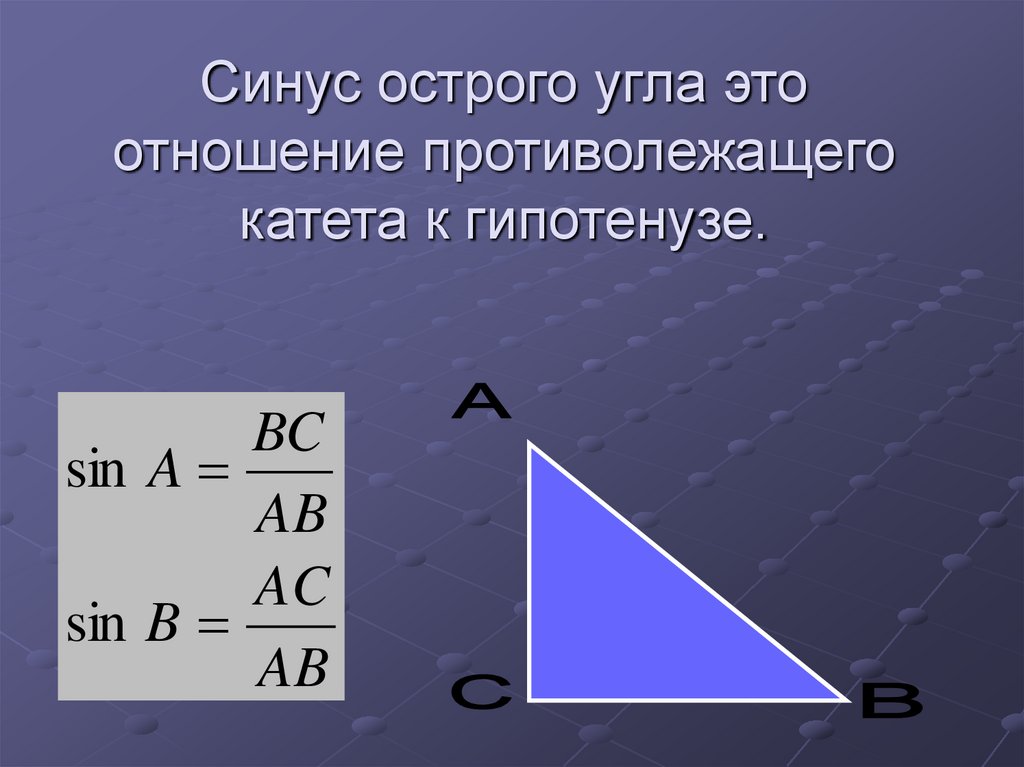
6. Синус острого угла это отношение противолежащего катета к гипотенузе.
BCsin A
AB
AC
sin B
AB
7. Косинус острого угла.
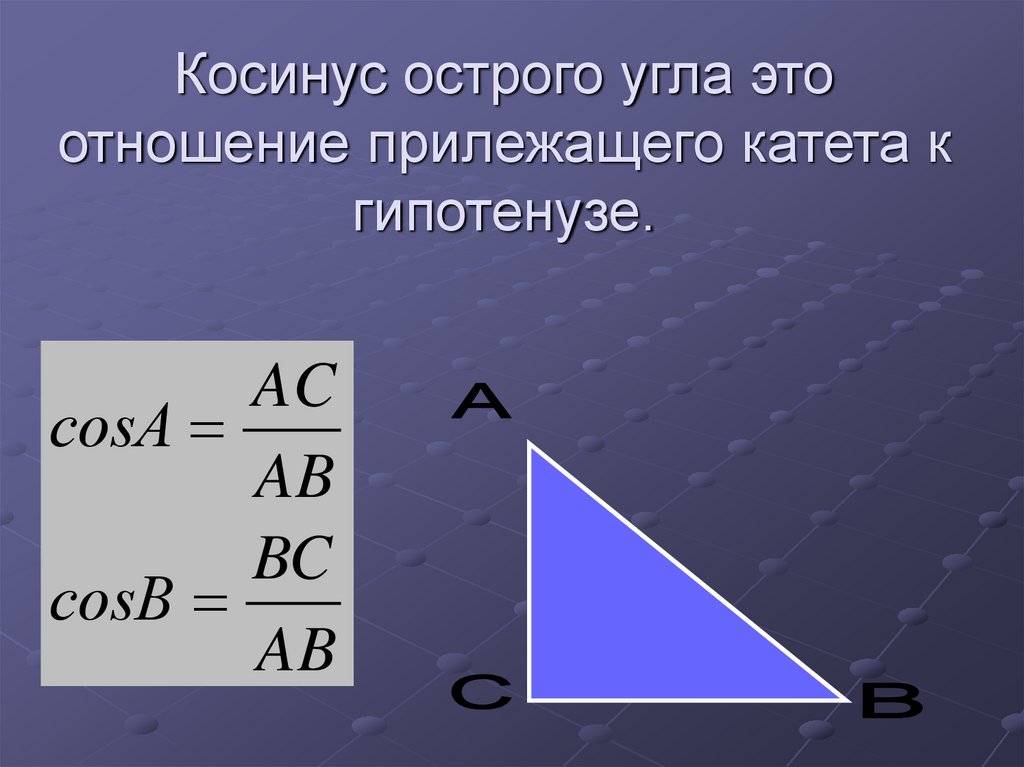
8. Косинус острого угла это отношение прилежащего катета к гипотенузе.
ACсosA
AB
BC
сosB
AB
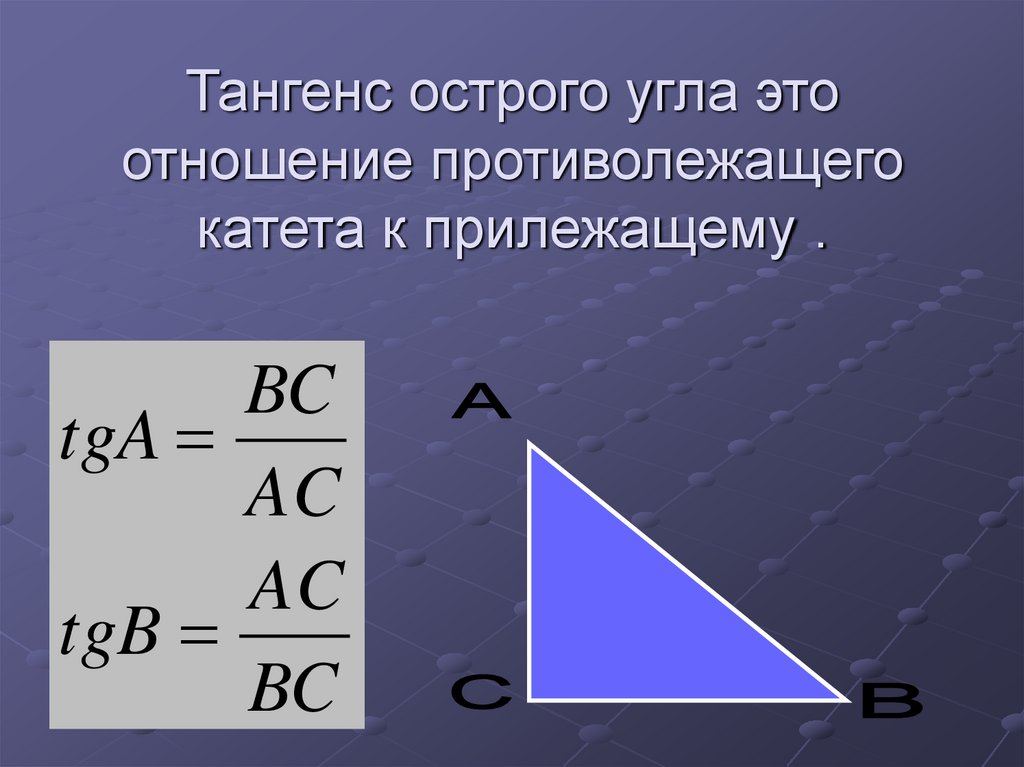
9. Тангенс острого угла.
10. Тангенс острого угла это отношение противолежащего катета к прилежащему .
BCtgA
AC
AC
tgB
BC
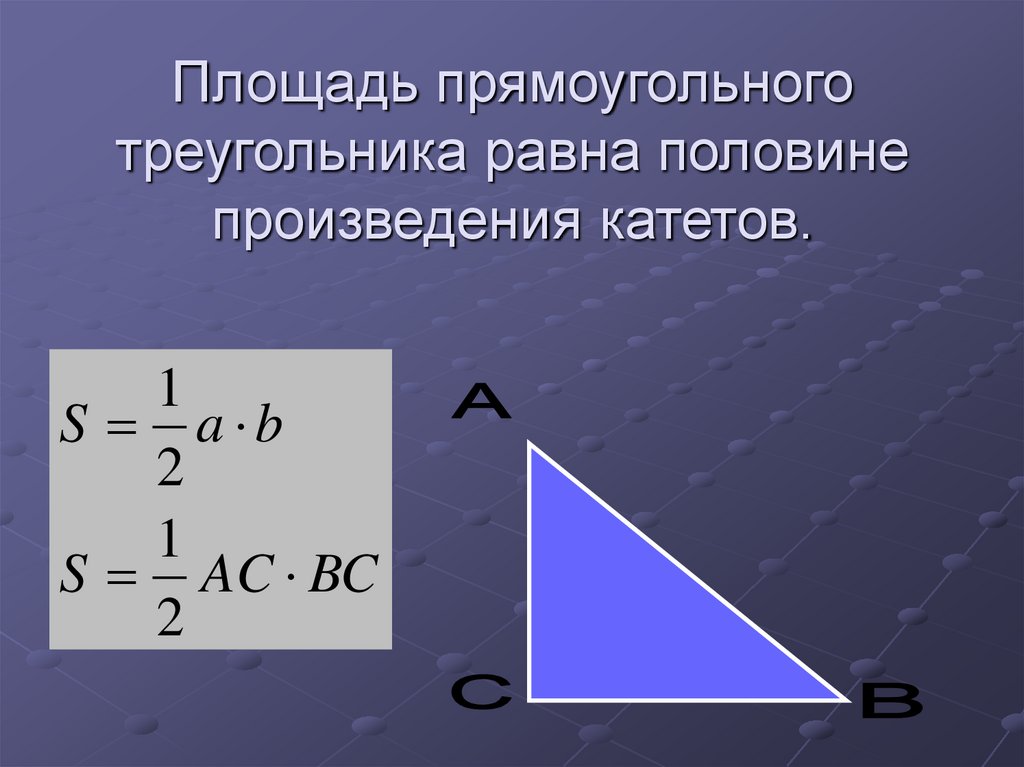
11. Площадь прямоугольного треугольника (используя катеты).
12. Площадь прямоугольного треугольника равна половине произведения катетов.
1S a b
2
1
S AC BC
2
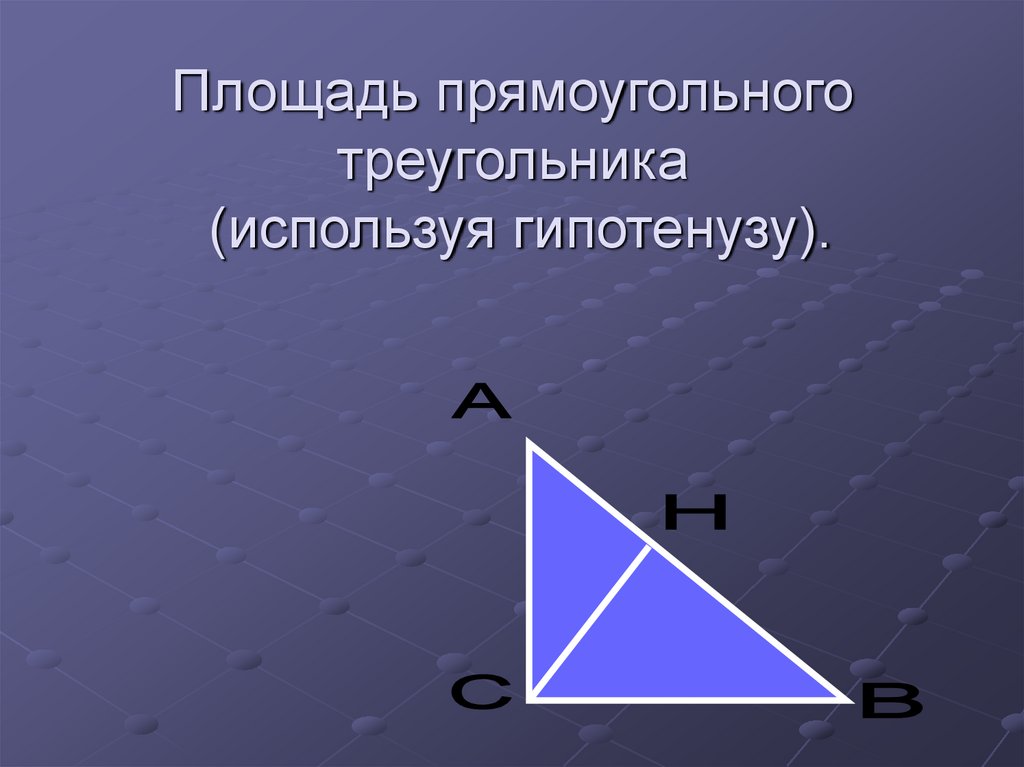
13. Площадь прямоугольного треугольника (используя гипотенузу).
14. Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, опущенную на неё.
1S c h
2
1
S AB CH
2
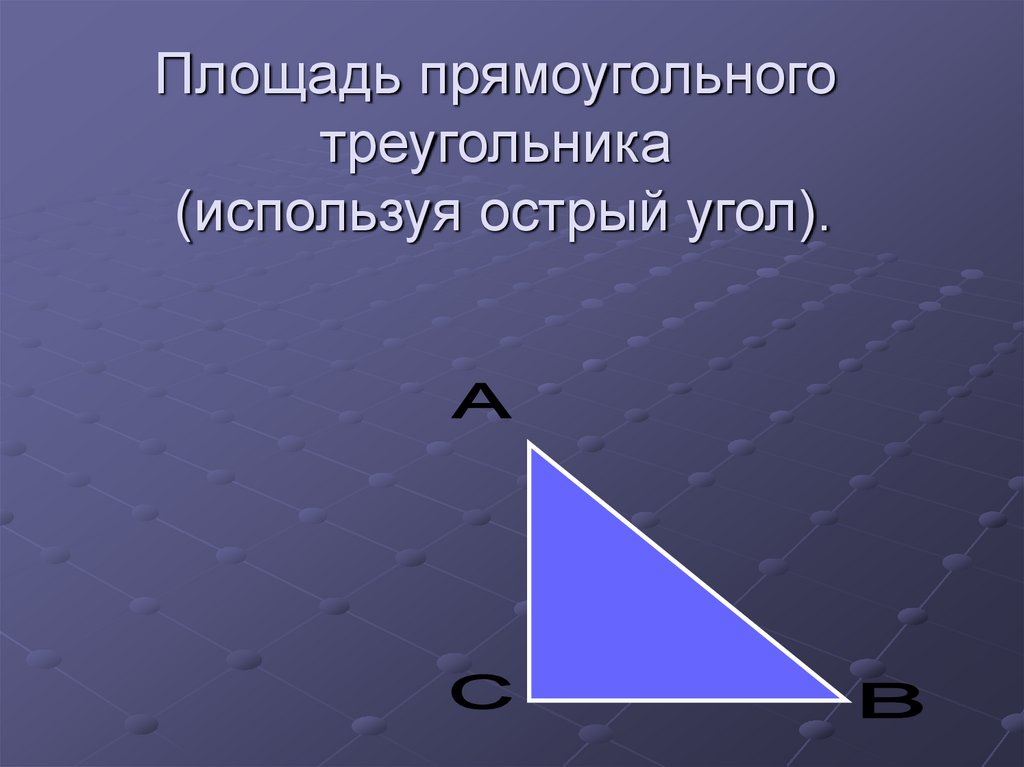
15. Площадь прямоугольного треугольника (используя острый угол).
16. Площадь прямоугольного треугольника равна половине произведения двух сторон на синус угла между ними.
1S AC AB sin A
2
1
S BC AB sin B
2
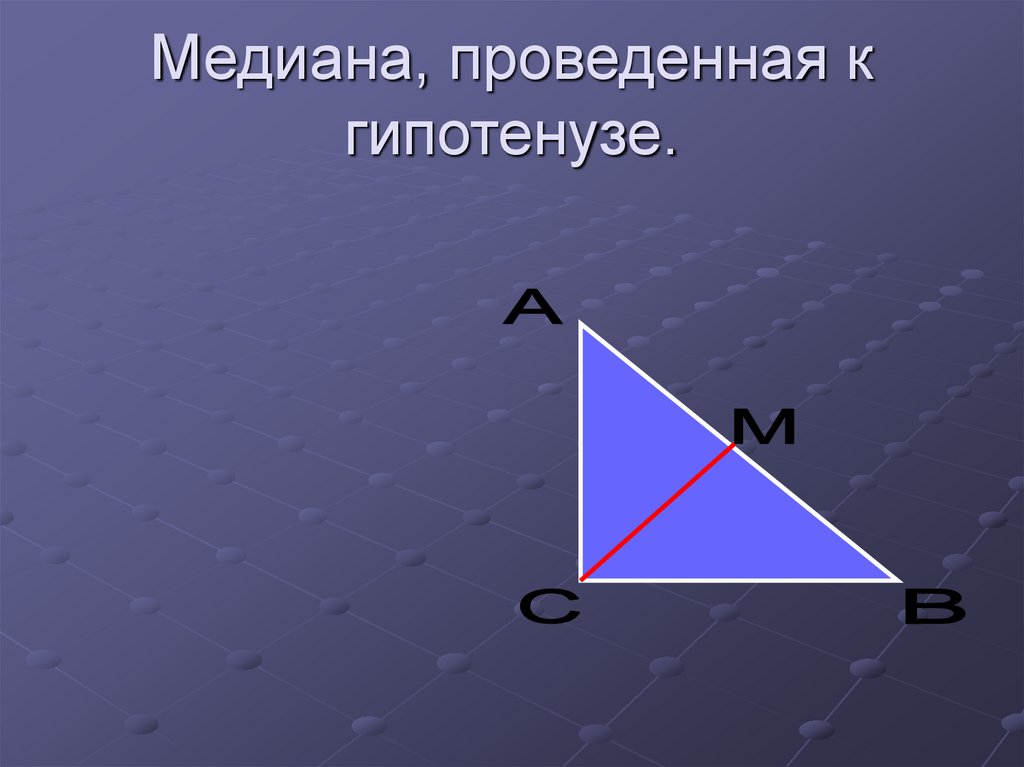
17. Медиана, проведенная к гипотенузе.
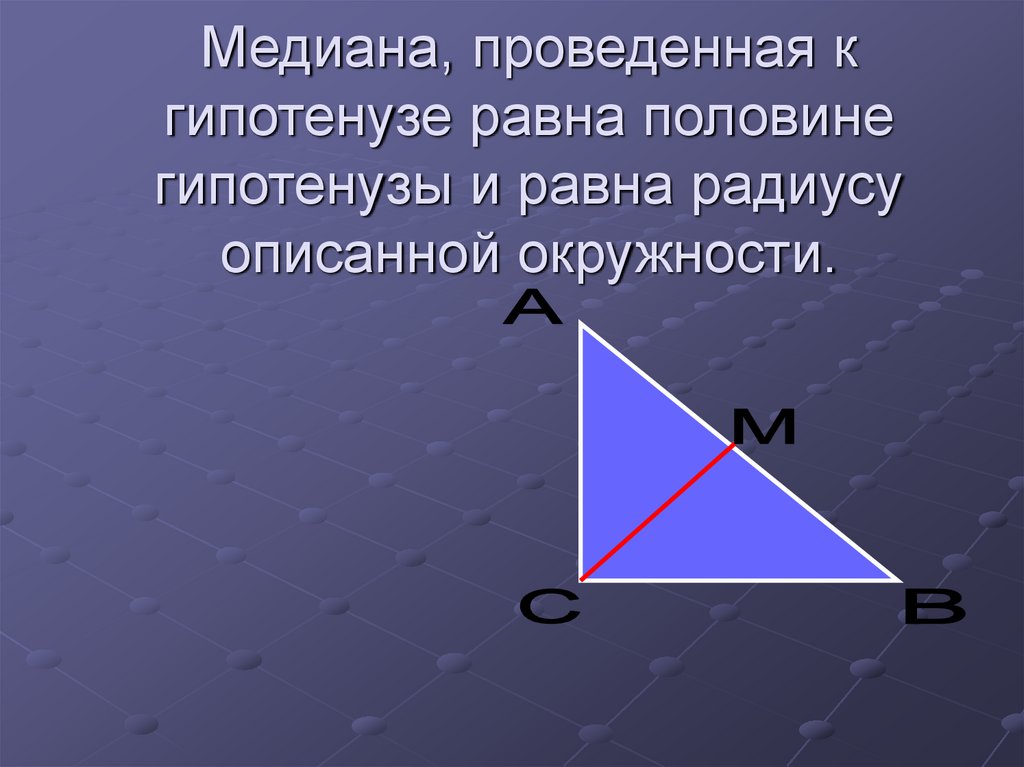
18. Медиана, проведенная к гипотенузе равна половине гипотенузы и равна радиусу описанной окружности.
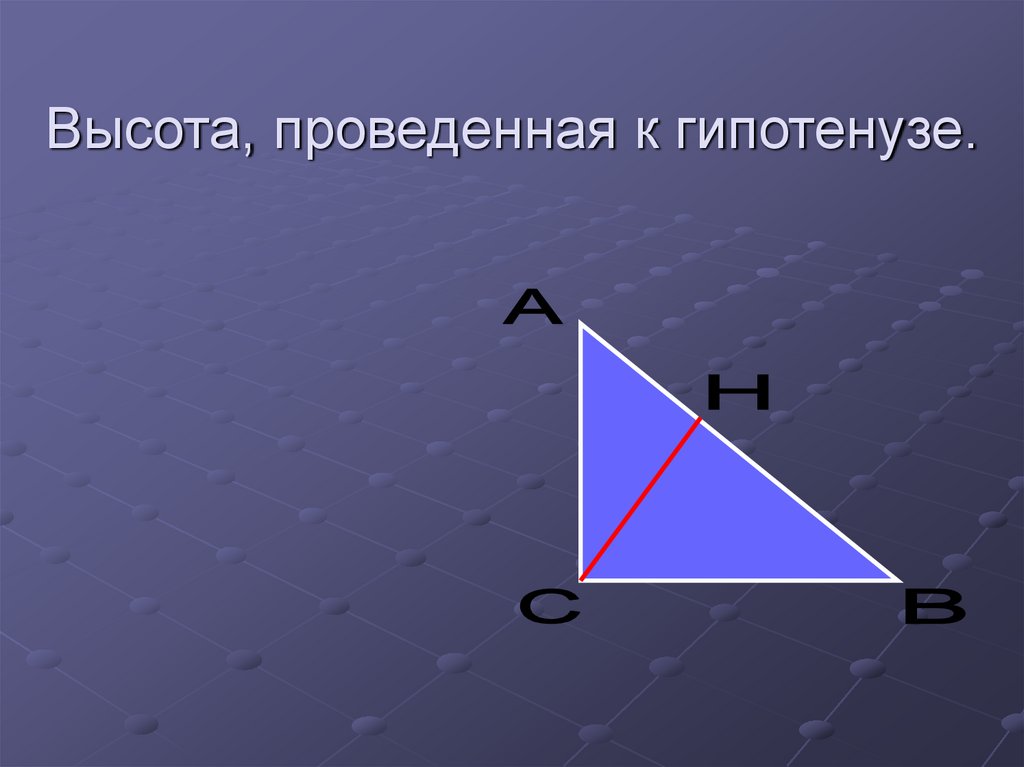
19. Высота, проведенная к гипотенузе.
20. Высота, проведенная к гипотенузе, есть среднее геометрическое между проекциями катетов.
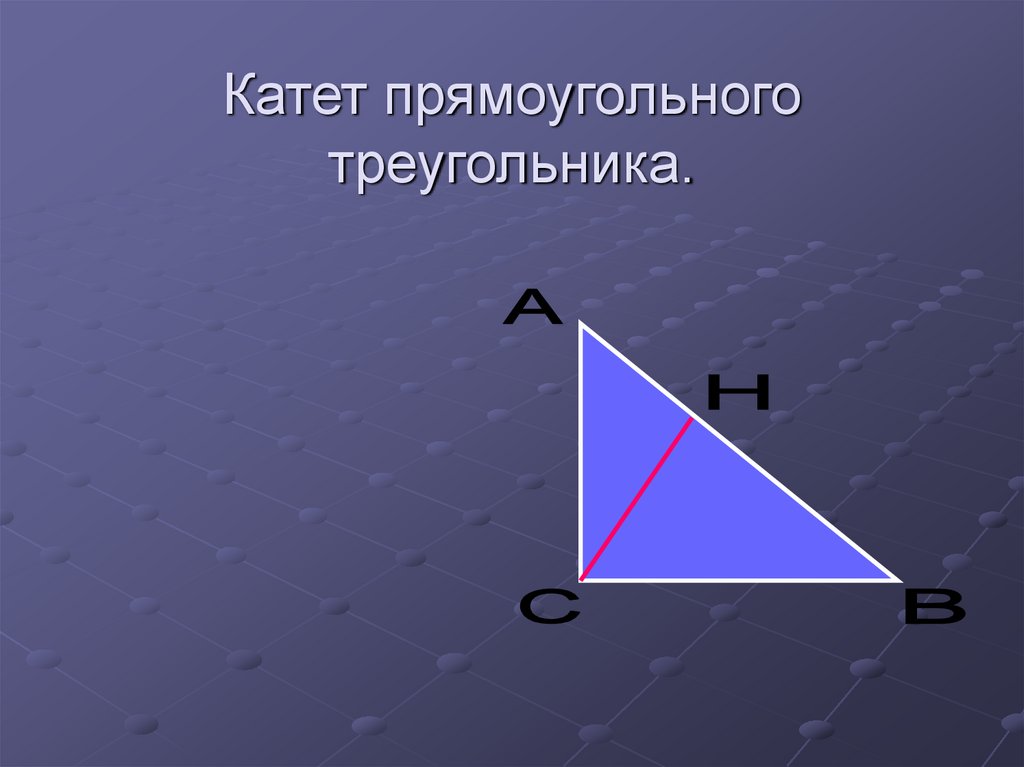
СH АH ВH21. Катет прямоугольного треугольника.
22. Катет прямоугольного треугольника есть среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу.
СА АН АВСВ ВН АВ








 Математика
Математика








