Похожие презентации:
Методы нахождения расстояний между скрещивающимися прямыми
1. Методы нахождения расстояний между скрещивающимися прямыми.
Автор : Сигодина Лариса Владимировна,учитель математики
МБОУ «БСОШ №1 им. П. П. Корягина»
Благовещенского района Алтайского края
2016
2. Методы нахождения расстояний между скрещивающимися прямыми.
Определение 1: Расстоянием междускрещивающимися прямыми называется расстояние
между ближайшими точками этих прямых.
Определение2: Расстояние между
скрещивающимися прямыми называется длина их
общего перпендикуляра.
Определение 3: … называется расстояние между их
проекциями на плоскость, перпендикулярную одной
из этих прямых.
Определение 4: …называется расстояние от одной
из скрещивающихся прямых до параллельной
плоскости, проходящей через другую прямую.
Определение 5:… называется расстояние между
параллельными плоскостями, в которых находятся
скрещивающиеся прямые.
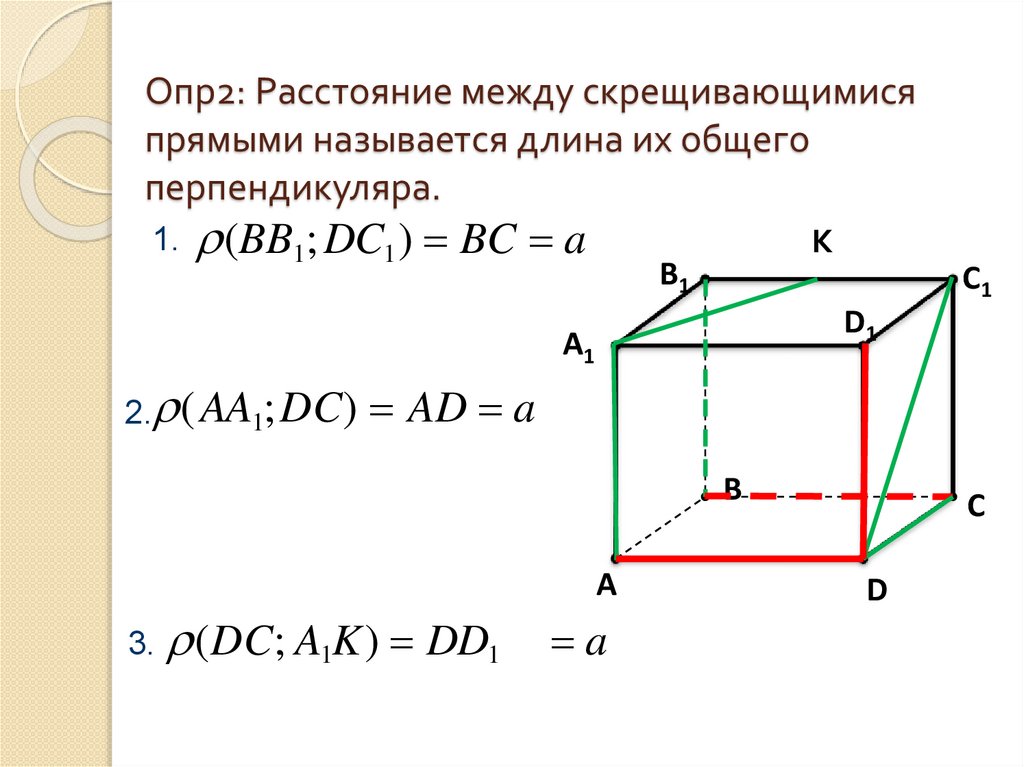
3. Опр2: Расстояние между скрещивающимися прямыми называется длина их общего перпендикуляра.
1.(BB1; DC1 ) BC a
К
B1
C1
D1
A1
2. ( AA1;DC)
AD a
B
A
3.
(DC; A1K) DD1
a
C
D
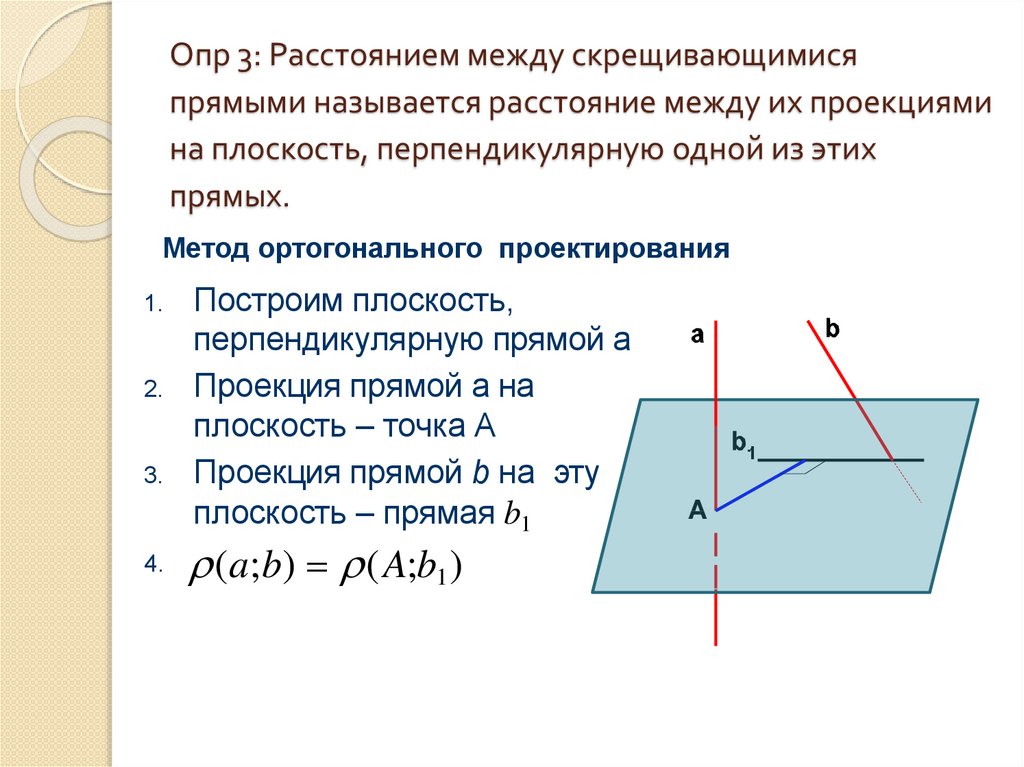
4. Опр 3: Расстоянием между скрещивающимися прямыми называется расстояние между их проекциями на плоскость, перпендикулярную одной
из этихпрямых.
Метод ортогонального проектирования
1.
2.
3.
4.
Построим плоскость,
перпендикулярную прямой a
Проекция прямой а на
плоскость – точка А
Проекция прямой b на эту
плоскость – прямая b1
(a;b) ( A;b1 )
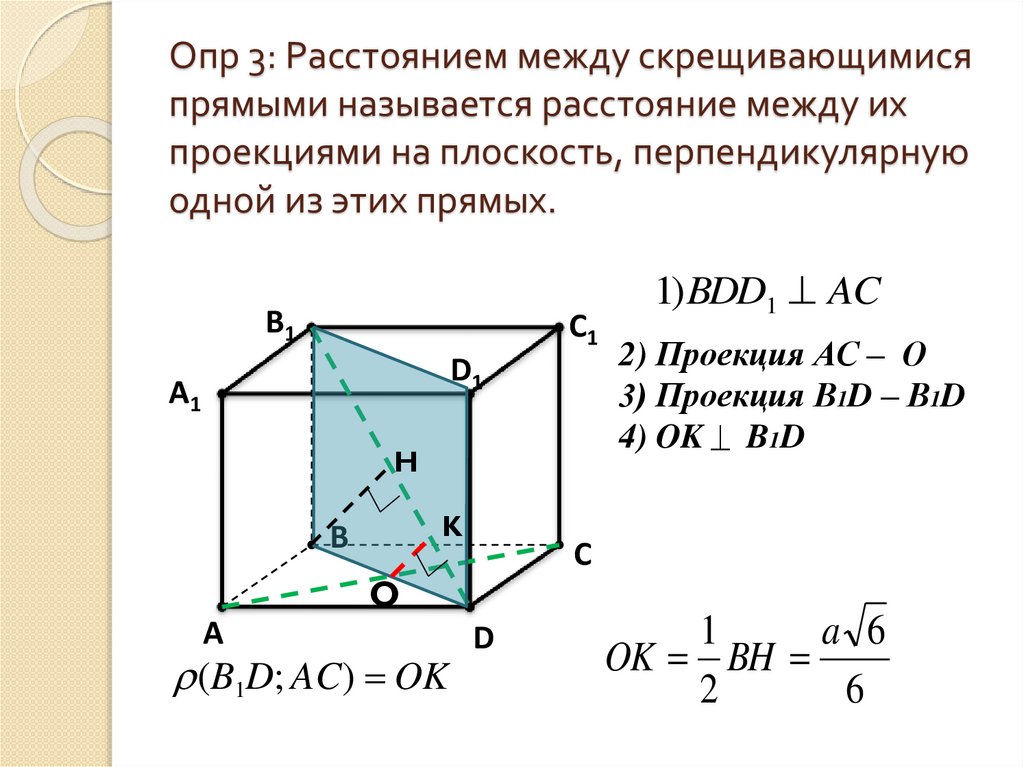
5. Опр 3: Расстоянием между скрещивающимися прямыми называется расстояние между их проекциями на плоскость, перпендикулярную одной
из этих прямых.B1
C1
D1
A1
H
K
B
1) BDD1 AC
2) Проекция АС – О
3) Проекция В1D – В1D
4) OK B1D
C
O
A
(B1D; AC) OK
D
1
a 6
OK BH
2
6
6.
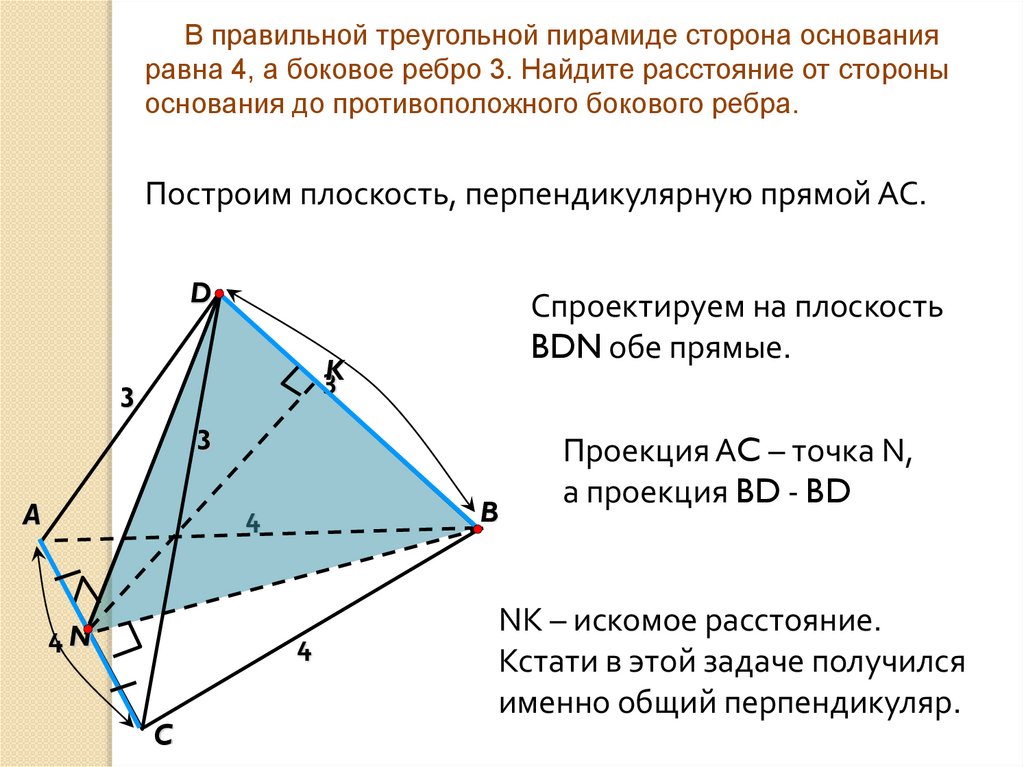
В правильной треугольной пирамиде сторона основанияравна 4, а боковое ребро 3. Найдите расстояние от стороны
основания до противоположного бокового ребра.
Построим плоскость, перпендикулярную прямой АС.
D
Спроектируем на плоскость
BDN обе прямые.
3K
3
3
A
B
4
4N
4
C
Проекция АC – точка N,
а проекция BD - BD
NK – искомое расстояние.
Кстати в этой задаче получился
именно общий перпендикуляр.
7.
Найдем высоту DBN .Из BCN :
BC 2 CN 2 BN 2 ;
Из DCN :
BN 2 3.
CD2 CN 2 DN 2 ;
DN 5.
D
3
3
5
A
4
4
N
4
2
C
Составим систему уравнений.
2
2
2
2
3
h
3
x
2
2
2
5 h x
2
2
12
h
9
6
х
x
«–»
2
2
5
h
x
7 9 6 х;
6 х 9 7;
1
х .
3
1
Подставим во второе уравнение 5 h ;
9
K 3
D
1
2
h
5
;
5
9
x
К 3
8
h
N
h2 4 ;
3-x
9
B
44
2 3
h
;
9
В
2
2 11
h
.
3
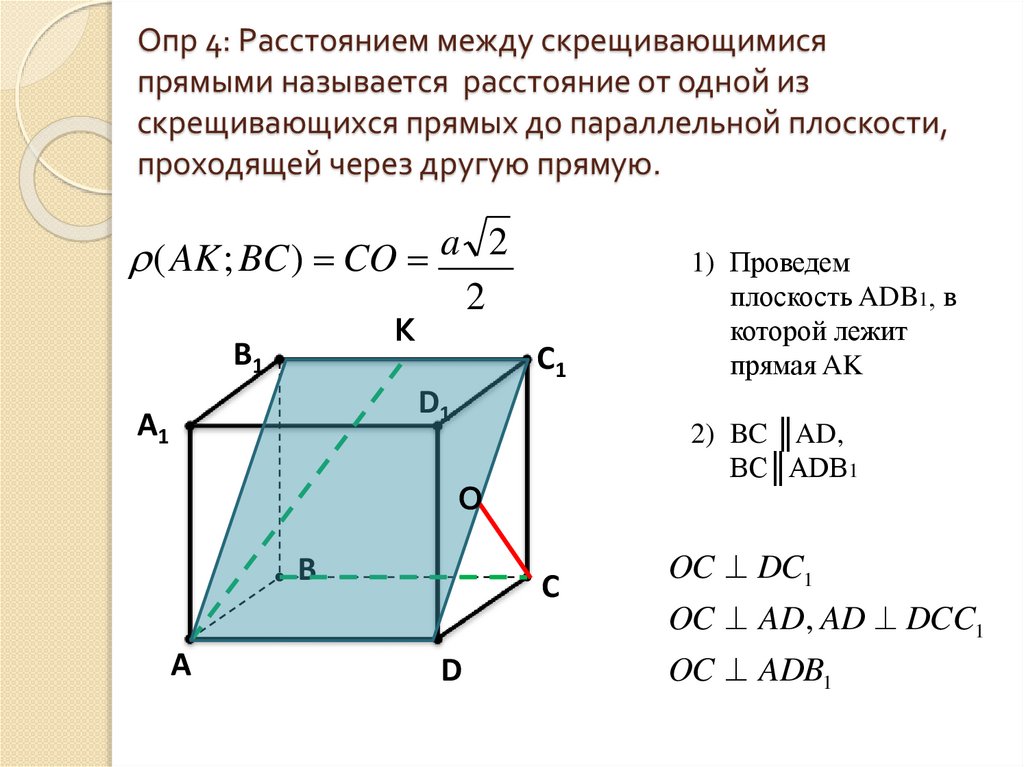
8. Опр 4: Расстоянием между скрещивающимися прямыми называется расстояние от одной из скрещивающихся прямых до параллельной
плоскости,проходящей через другую прямую.
(AK; BC) CO a 2
2
К
B1
C1
D1
A1
1) Проведем
плоскость ADB1, в
которой лежит
прямая AK
2) BC ║AD,
BC║ADB1
О
B
A
C
D
OC DC1
OC AD, AD DCC1
OC ADB1
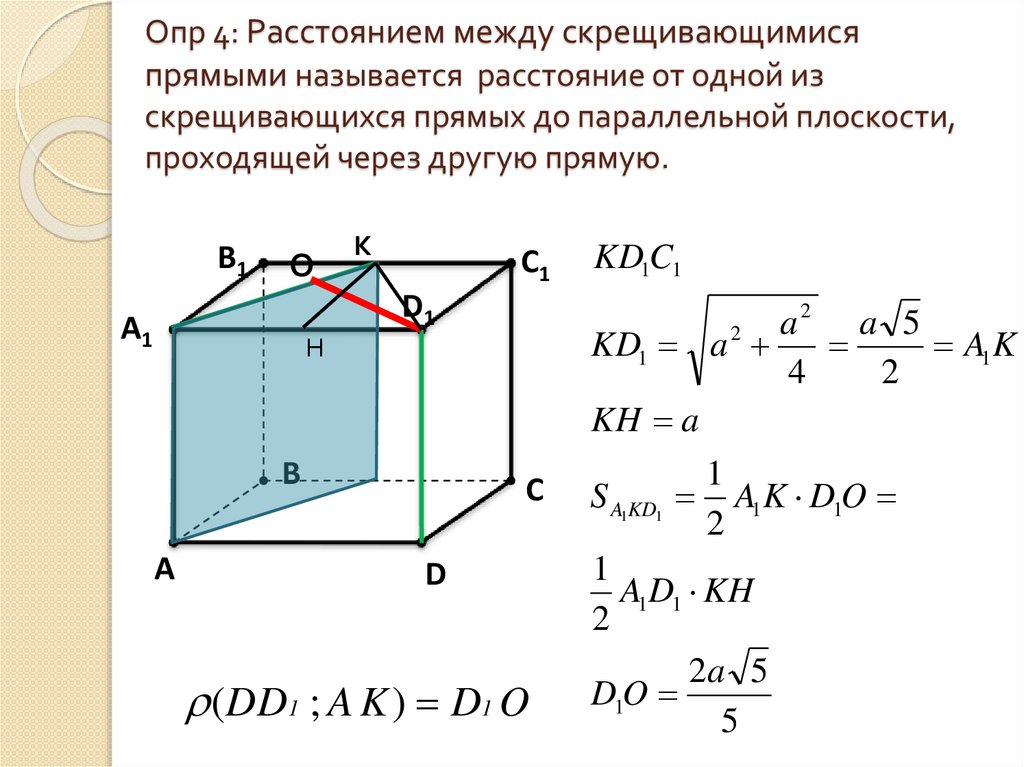
9. Опр 4: Расстоянием между скрещивающимися прямыми называется расстояние от одной из скрещивающихся прямых до параллельной
плоскости,проходящей через другую прямую.
B1
О
К
C1
D1
A1
2
a
a 5
2
KD1 a
A1K
4
2
KH a
H
B
A
KD1C1
C
D
(DD1 ; A K ) D1 O
S A1KD1
1
A1K D1O
2
1
A1D1 KH
2
2a 5
D1O
5
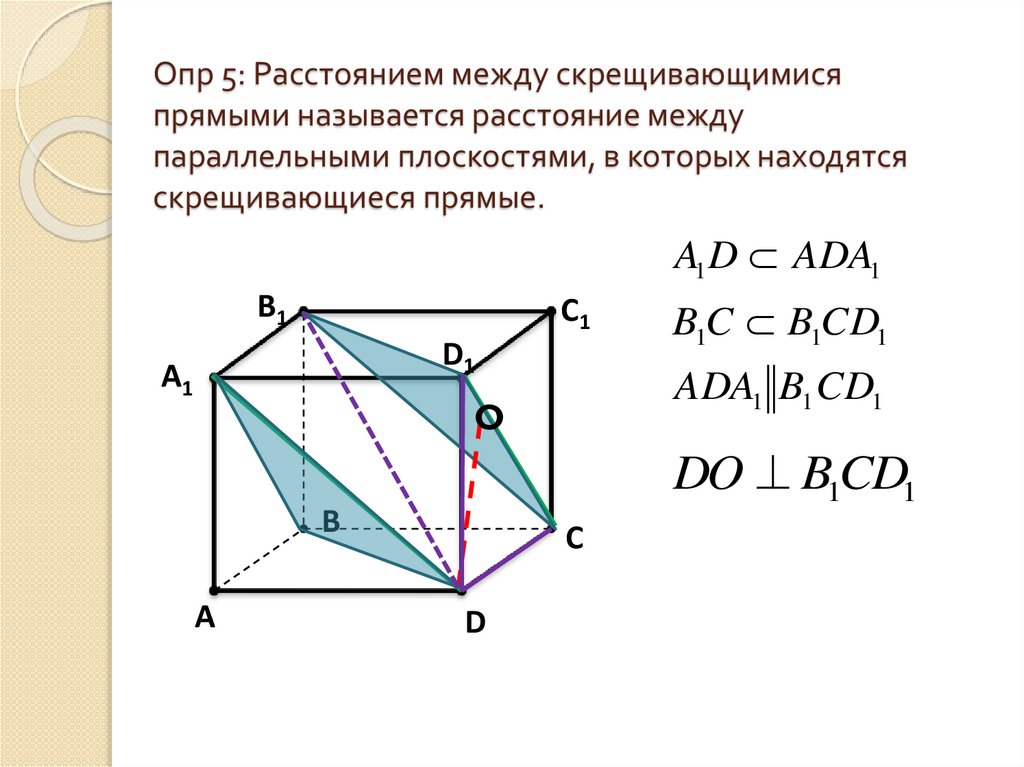
10. Опр 5: Расстоянием между скрещивающимися прямыми называется расстояние между параллельными плоскостями, в которых находятся
скрещивающиеся прямые.A1 D ADA1
B1
C1
D1
A1
ADA1 B1 CD1
O
DO B1CD1
B
A
B1C B1CD1
C
D
11.
DD1 DC 1 наклонныеB1 CD1 правильный
O1D OC проекции
6
ВН
2
СDD1 равнобед.
О ВН серединный
перпендику ляр
D
DH
1
3
1
O
2
D1
BDH
1
cos H
3
6
sin H
3
2
B1
2
2
H
2
С
DOH
DO DH sin H
3
DO
3
12. Метод координат
1. Ввести «удобным» способом системукоординат.
2. Найти координаты «нужных» точек.
3. Записать уравнение плоскости.
4. Вычислить расстояние по формуле.
M x0 ; y0 ; z0 до плоскости
Расстояние от точки
ax by cz d 0
Вычисляется по формуле:
ax0 by0 cz0 d
a b c
2
2
2
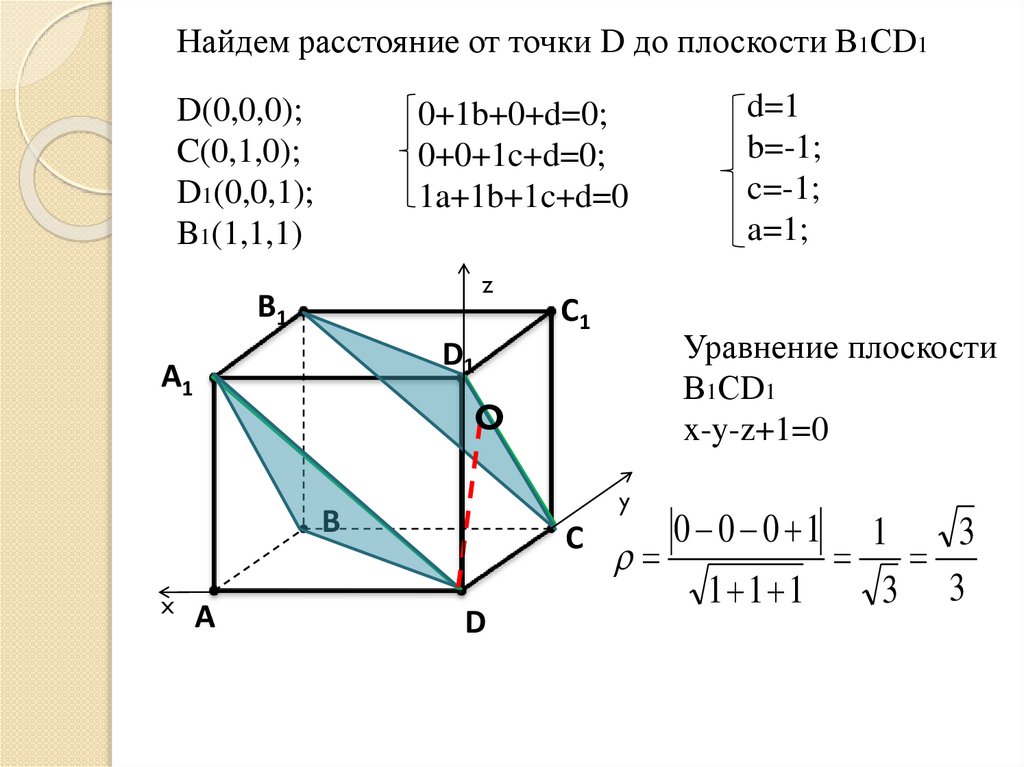
13.
Найдем расстояние от точки D до плоскости В1СD1D(0,0,0);
C(0,1,0);
D1(0,0,1);
B1(1,1,1)
0+1b+0+d=0;
0+0+1c+d=0;
1a+1b+1c+d=0
z
B1
Уравнение плоскости
В1СD1
x-y-z+1=0
D1
A1
O
y
B
x
C1
A
C
D
d=1
b=-1;
c=-1;
a=1;
0 0 0 1
1
3
1 1 1
3 3
14.
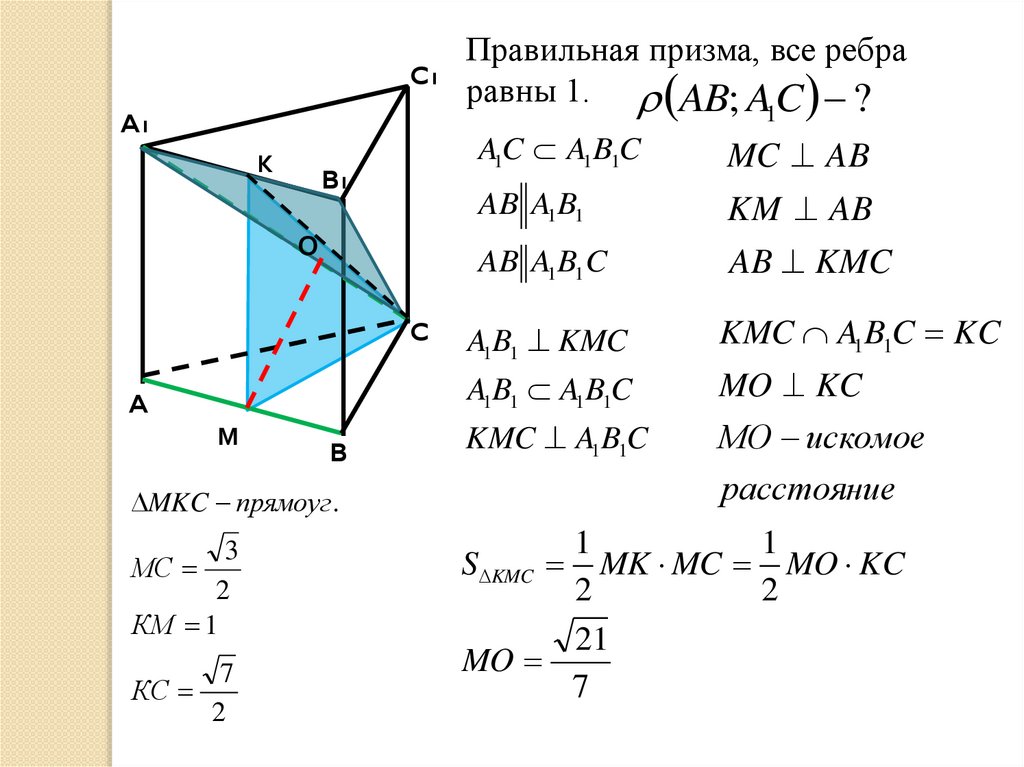
C1Правильная призма, все ребра
равны 1. AB; A C ?
1
A1
К
B1
О
C
A
М
B
A1C A1B1C
MC AB
AB A1B1
KM AB
AB A1B1 C
AB KMC
A1B1 KMC
A1B1 A1B1C
MO KC
KMC A1B1C
МО искомое
расстояние
MKC прямоуг .
3
МС
2
КМ 1
КС
7
2
KMC A1B1C KC
1
1
MK MC MO KC
2
2
21
MO
7
S KMC
15.
C1A1
z
B1
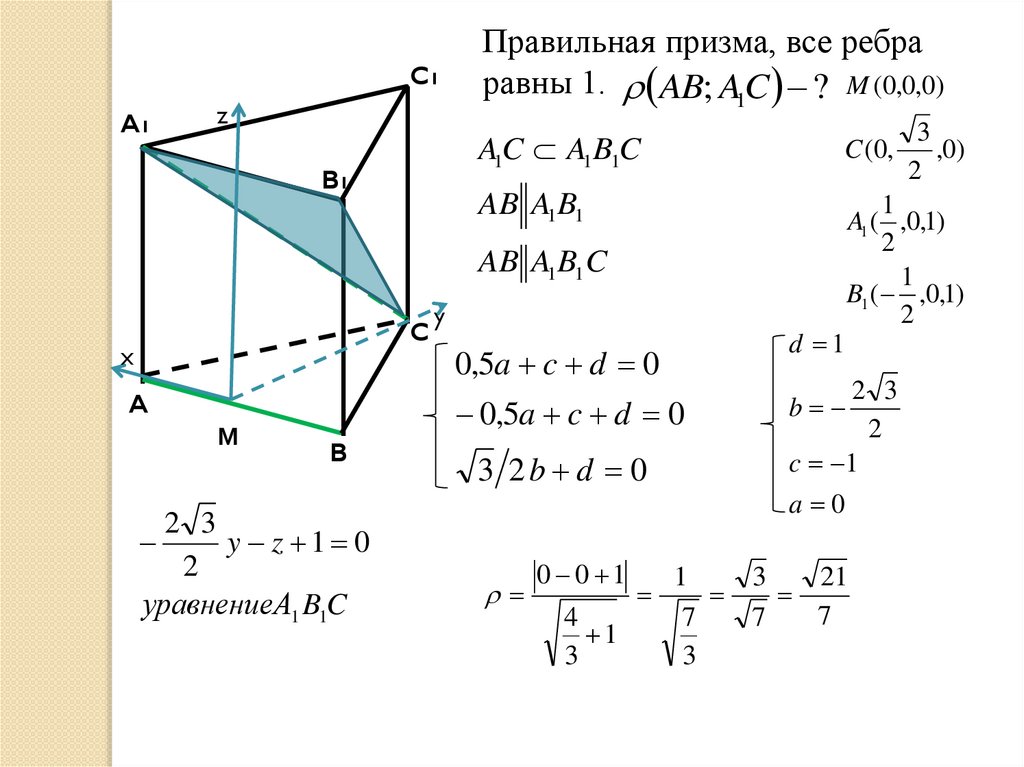
Правильная призма, все ребра
равны 1. AB; A1C ? M (0,0,0)
A1C A1B1C
AB A1B1
1
A1 ( ,0,1)
2
1
B1 ( ,0,1)
2
AB A1B1 C
C
x
A
М
y
d 1
0,5a c d 0
0,5a c d 0
B
2 3
y z 1 0
2
уравнениеA1 B1C
3
,0)
2
C (0,
3 2b d 0
0 0 1
4
1
3
2 3
2
c 1
b
a 0
1
3
21
7
7
7
3
16.
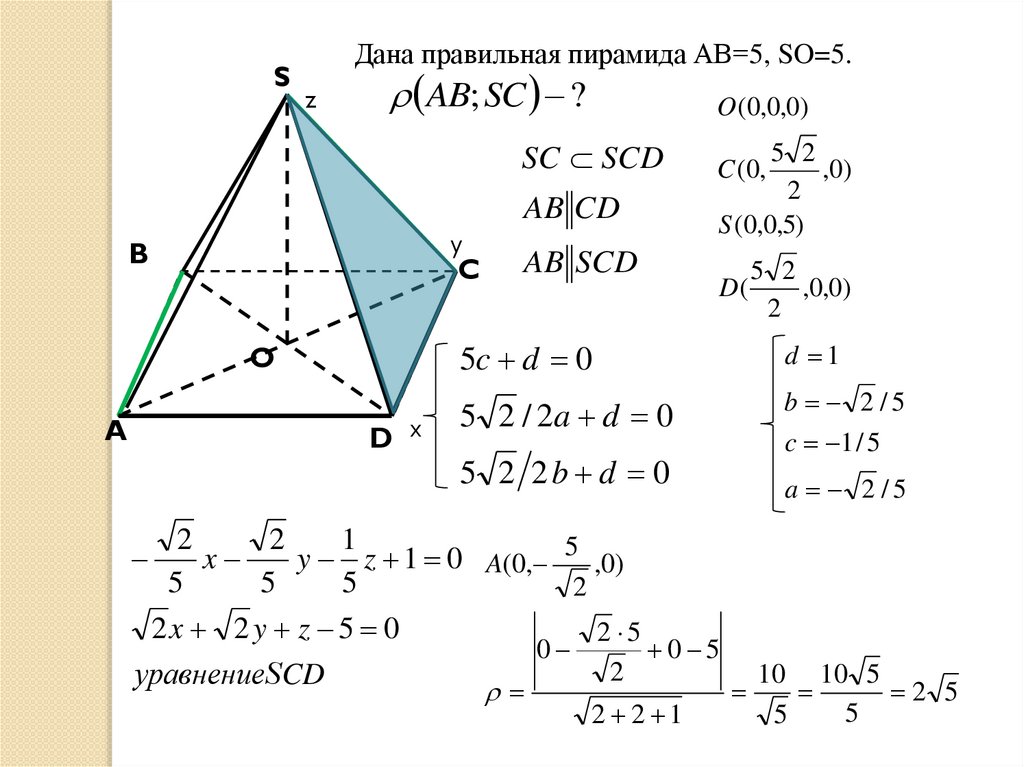
SДана правильная пирамида АВ=5, SO=5.
z
AB; SC ?
O (0,0,0)
SC SCD
AB CD
у
B
C
O
A
D х
AB SCD
5 2
,0)
2
S (0,0,5)
C (0,
D(
5 2
,0,0)
2
5c d 0
d 1
5 2 / 2a d 0
b 2 /5
c 1 / 5
5 2 2b d 0
2
2
1
x
y z 1 0 A(0, 5 ,0)
5
5
5
2
2x 2 y z 5 0
2 5
0
0 5
2
уравнениеSCD
a 2 /5
2 2 1
10 10 5
2 5
5
5
17. Метод координат
1. Расстояние от точки до плоскости.2. Расстояние между плоскостью и параллельной ей
прямой.
3. Расстояние между параллельными плоскостями.
4. Расстояние между скрещивающимися прямыми.
M x0 ; y0 ; z0 до плоскости
Расстояние от точки
ax by cz d 0
Вычисляется по формуле:
ax0 by0 cz0 d
a b c
2
2
2
18. Интернет ресурсы:
http://nsportal.ru/shkola/geometriya/library/2012/11/26/master-klass-nakhozhdenierasstoyaniya-mezhduhttp://www.myshared.ru/slide/478172/







 Инженерная графика
Инженерная графика








