Параметрические характеристики параболы

1.

2.

Параметр (от греч. παραμετρωυ отмеривающий )- величина,
значение которой служит для различия
элементов некоторого множества между
собой.
Парабола ( от греч. παραβολη –
приложение ) – ввел название Апполоний
Пергский ( ок. 200 до н.э.) как одно из
конических сечений.
ПОСМОТРИМ В СЛОВАРЕ

3.

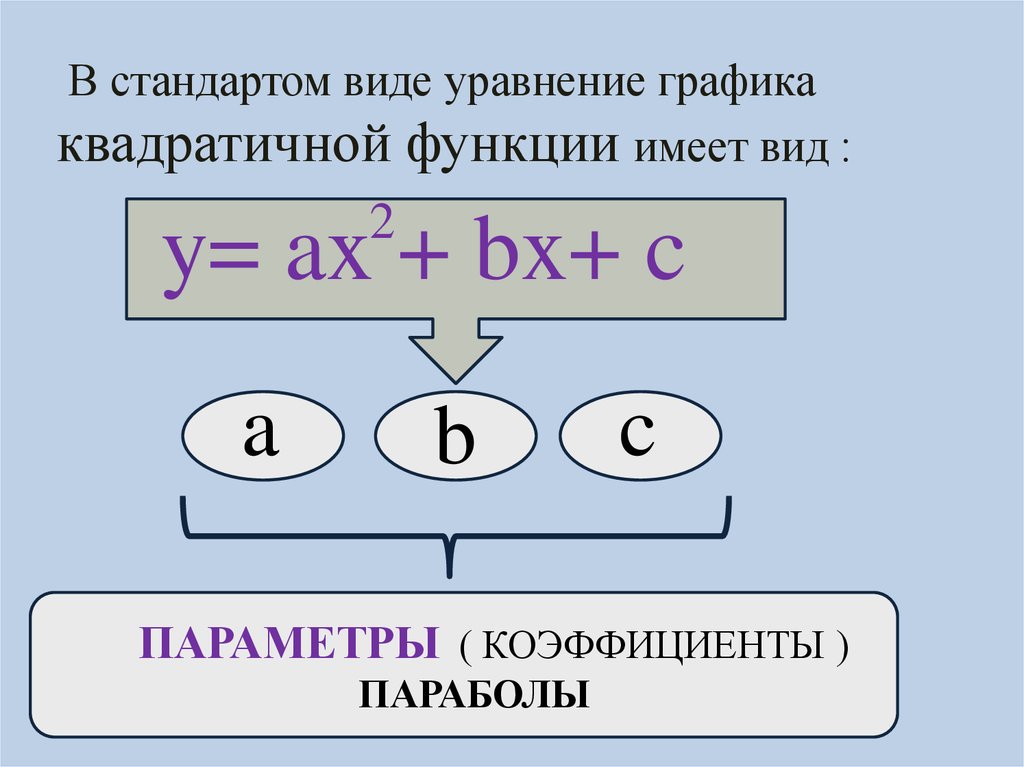
В стандартом виде уравнение графика
квадратичной функции имеет вид :
2
y= ax + bx+ c
a
b
c
ПАРАМЕТРЫ ( КОЭФФИЦИЕНТЫ )
ПАРАБОЛЫ

4.

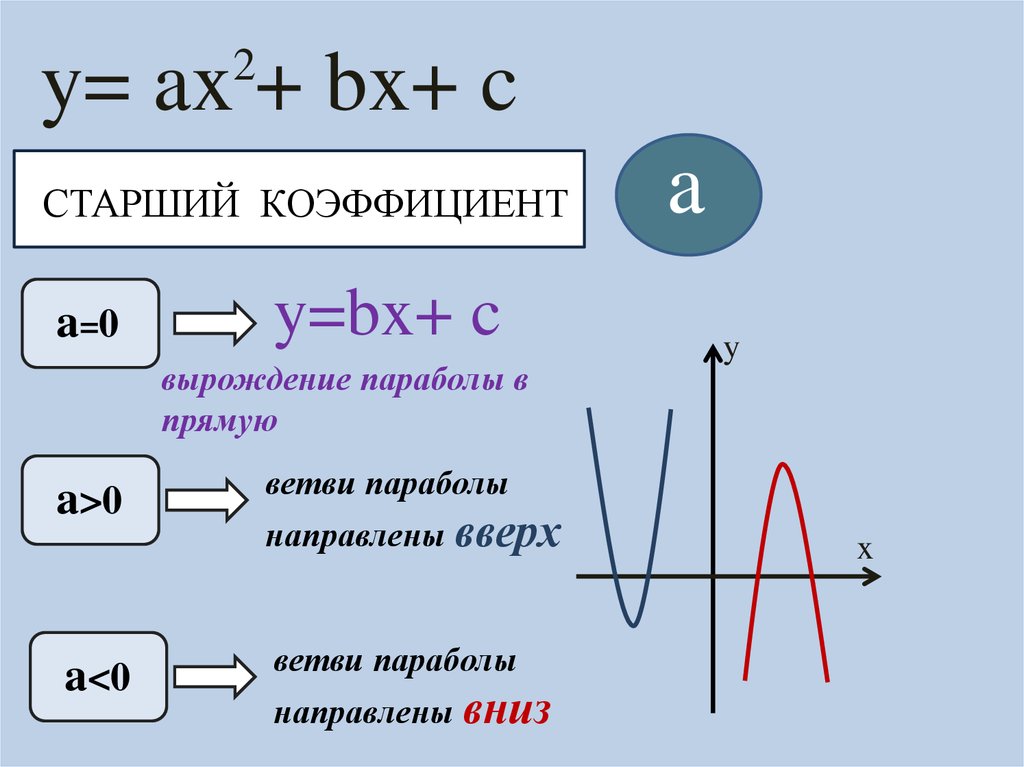
2
y= ax + bx+ c
СТАРШИЙ КОЭФФИЦИЕНТ
a=0
y=bx+ c
вырождение параболы в
прямую
a>0
a<0
a
y
ветви параболы
направлены вверх
ветви параболы
направлены вниз
x

5.

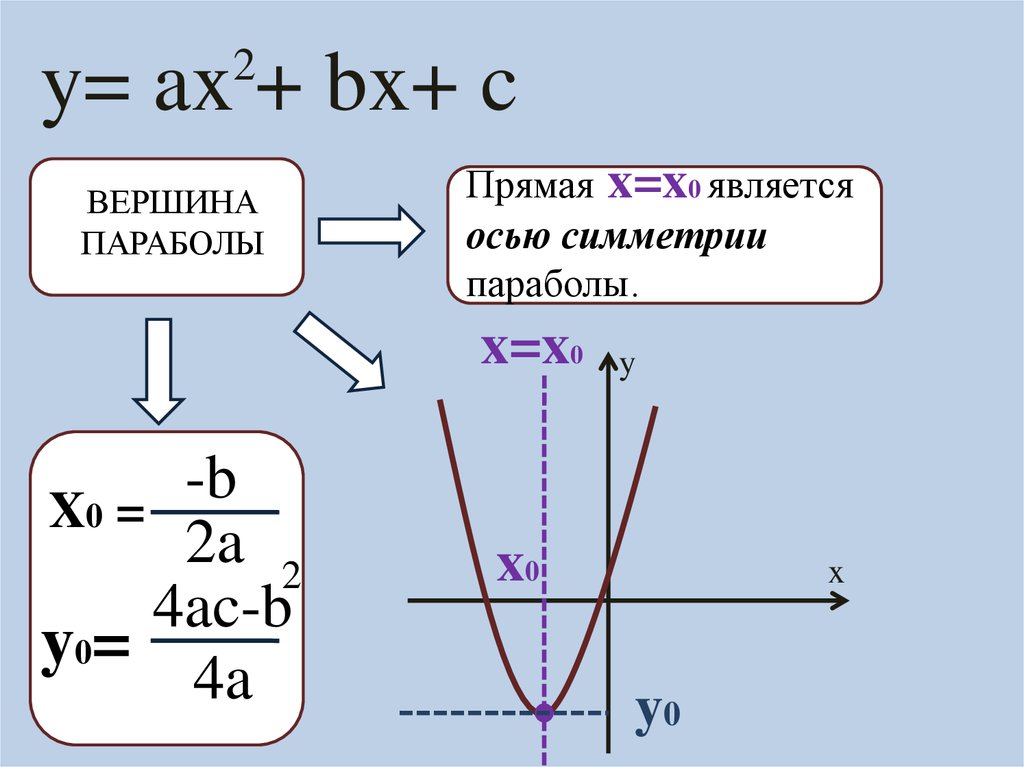
2
y= ax + bx+ c
ВЕРШИНА
ПАРАБОЛЫ
Прямая x=x0 является
осью симметрии
параболы.
x=x0
-b
X0 =
2a 2
4ac-b
y0=
4a
y
x0
x
y0

6.

2
y= x + (2k+1)x-5
ОПРЕДЕЛИТЬ
ПАРАМЕТР
k
0,5
При каких значениях
параметра k абсцисса
вершины параболы неотрицательное число?
a=1; b=2k+1; c=-5
□x
0=
-b
X0 =
2a 2 x0 ≥0
4ac-b
y0=
4a
-(2k-1)
= -k +0,5;
2
=> -k+0,5≥0;
-k≥-0,5;
k≤ 0,5 .
■

7.

Какое ЦЕЛОЕ ЗНАЧЕНИЕ р параметра
соответствует положительной абсциссе
вершины параболы?
1) p=12
2
y= 10x - (2p -1)x+3
РЕШЕНИЕ:
□X0=-b/2a;
X0=(2p-1)/20;
X0>0;
(2p-1)/20>0
p>0,5.■
ПРОВЕРЬ СЕБЯ
2) p=-7
3) p=-5
4) p=0
ВЕРНЫЙ ОТВЕТ
«ВЫДВИГАЕТСЯ»

8.

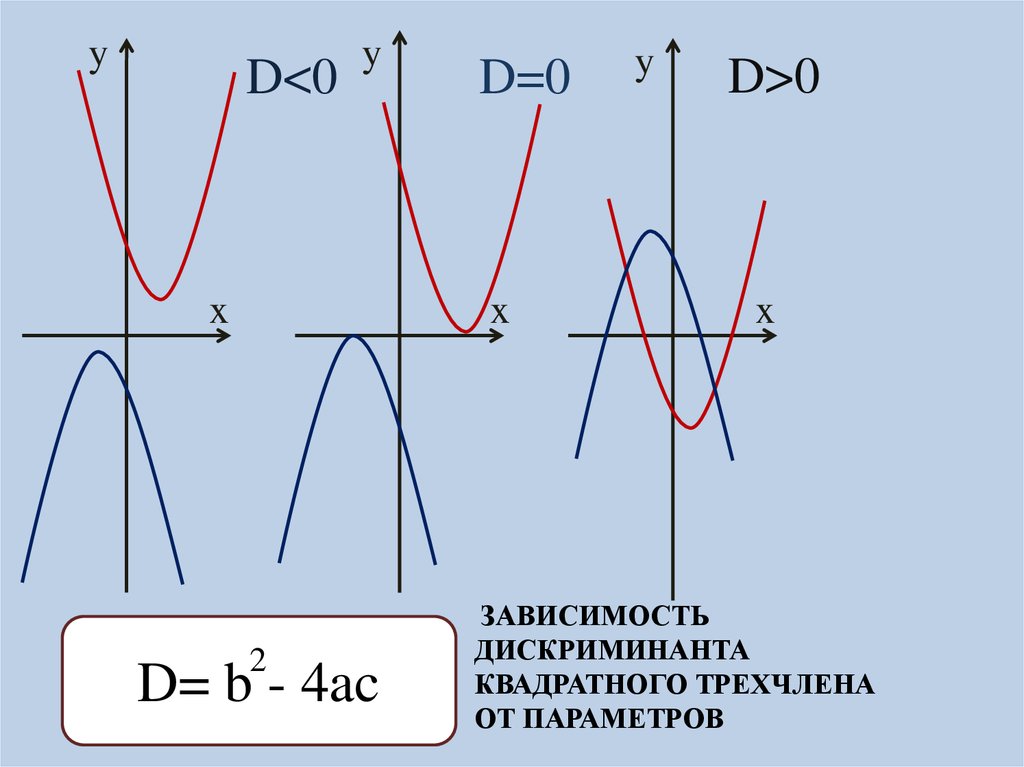
y
D<0
y
x
D=0
x
2
D= b - 4ac
y
D>0
x
ЗАВИСИМОСТЬ
ДИСКРИМИНАНТА
КВАДРАТНОГО ТРЕХЧЛЕНА
ОТ ПАРАМЕТРОВ

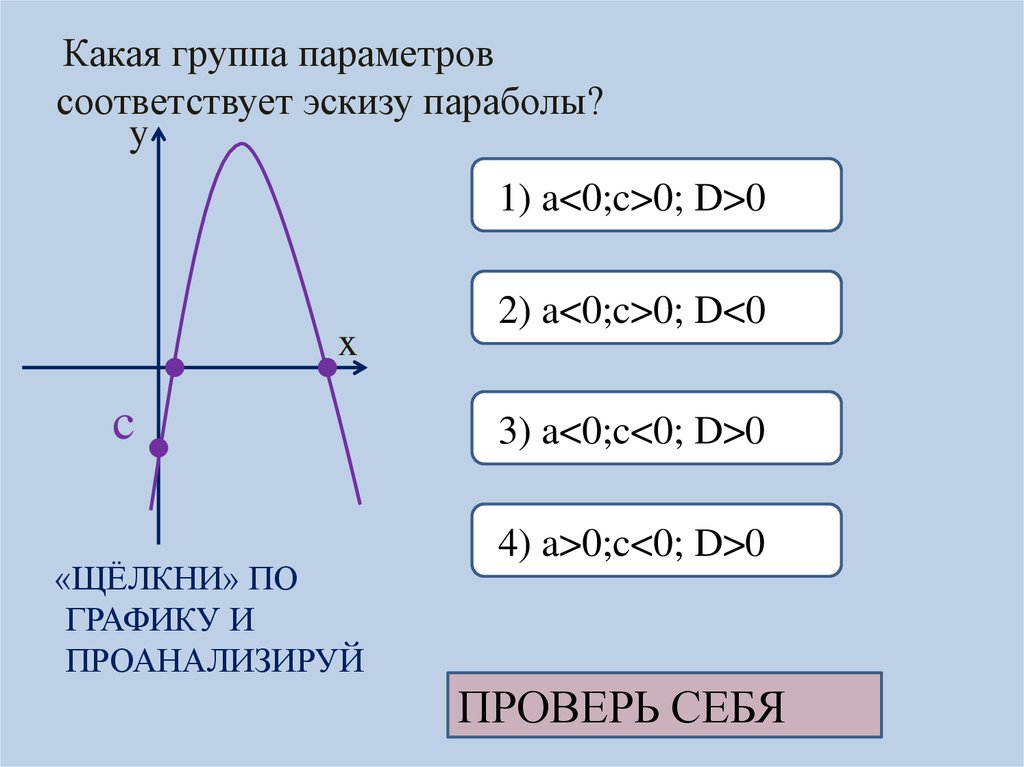
9.

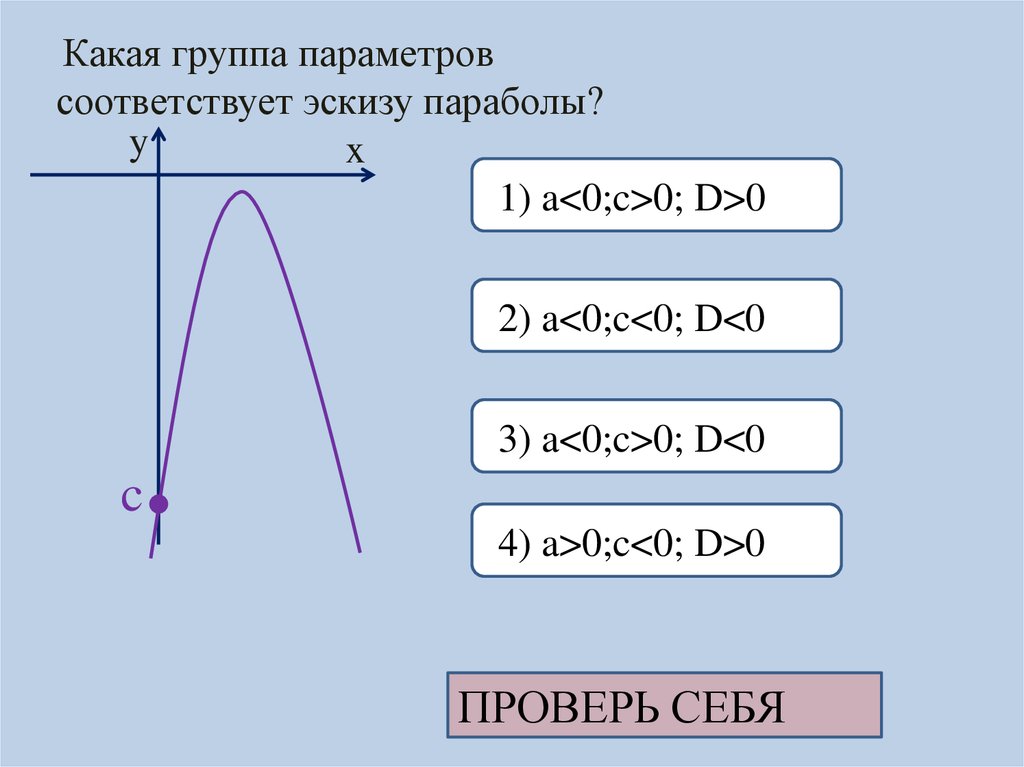
Какая группа параметров
соответствует эскизу параболы?
y
1) a<0;c>0; D>0
x
c
«ЩЁЛКНИ» ПО
ГРАФИКУ И
ПРОАНАЛИЗИРУЙ
2) a<0;c>0; D<0
3) a<0;c<0; D>0
4) a>0;c<0; D>0
ПРОВЕРЬ СЕБЯ

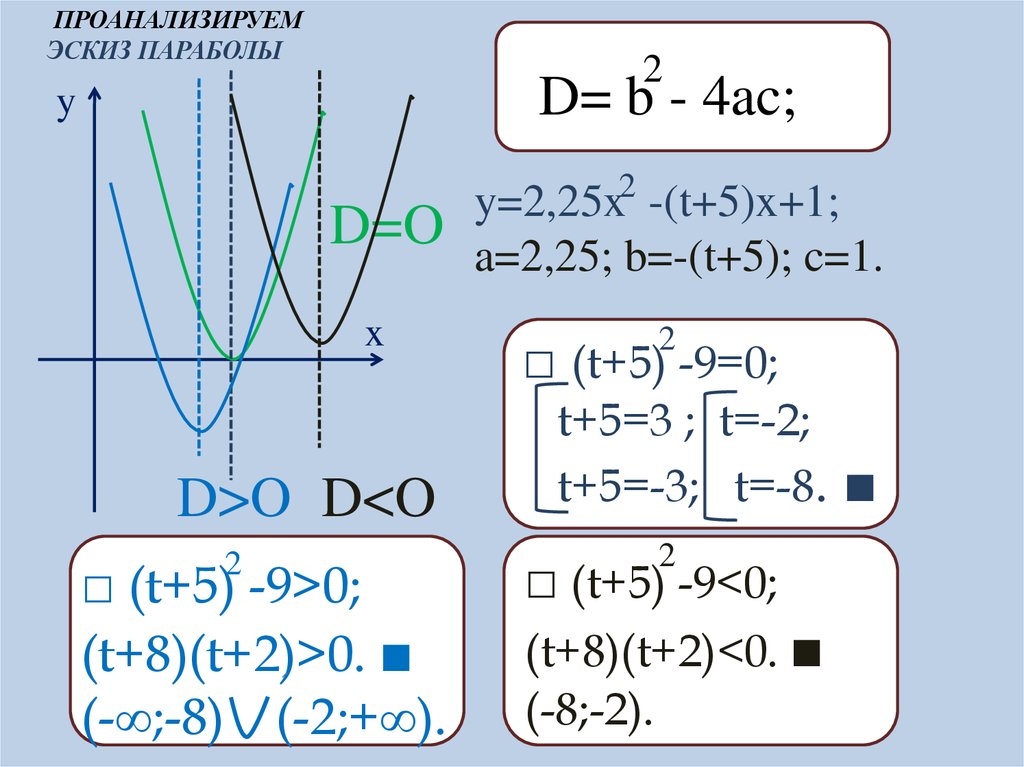
10.

ПРОАНАЛИЗИРУЕМ
ЭСКИЗ ПАРАБОЛЫ
2
D= b - 4ac;
y
D=O
x
D>O D<O
□ (t+5) -9>0;
2
(t+8)(t+2)>0. ■
(-∞;-8) (-2;+∞).
2
y=2,25x -(t+5)x+1;
a=2,25; b=-(t+5); c=1.
□ (t+5) -9=0;
2
t+5=3 ; t=-2;
t+5=-3; t=-8.
2
□ (t+5) -9<0;
(t+8)(t+2)<0. ■
(-8;-2).
■

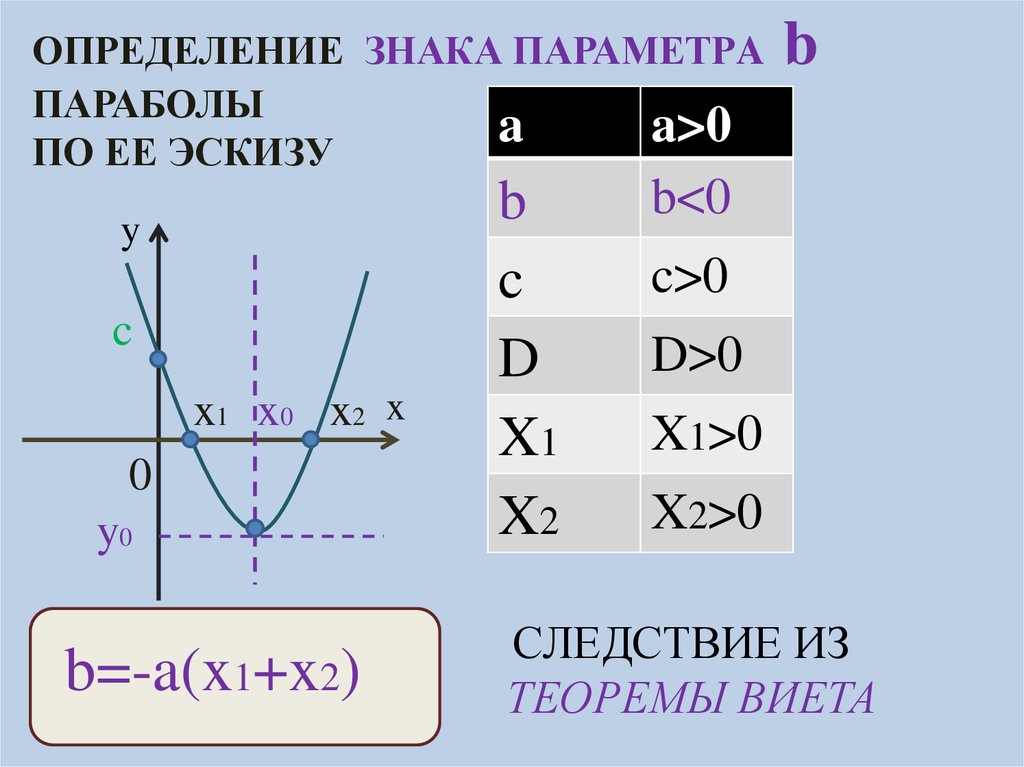
11.

ОПРЕДЕЛЕНИЕ ЗНАКА ПАРАМЕТРA
ПАРАБОЛЫ
a
a>0
ПО ЕЕ ЭСКИЗУ
y
c
x1 x0 x2 x
0
y0
b=-a(x1+x2)
b
c
D
X1
X2
b
b<0
c>0
D>0
X1>0
X2>0
СЛЕДСТВИЕ ИЗ
ТЕОРЕМЫ ВИЕТА

12.

ОПРЕДЕЛЕНИЕ ЗНАКА ПАРАМЕТРA b
ПАРАБОЛЫ
a>0
a
ПО ЕЕ ЭСКИЗУ
y
c
x1
x0 0
x2
y0
b=-a(x1+x2)
x
b
c
D
X1
X2
b>0
c>0
D>0
X1<0
X2<0
СЛЕДСТВИЕ ИЗ
ТЕОРЕМЫ ВИЕТА

13.

ОПРЕДЕЛЕНИЕ ЗНАКА ПАРАМЕТРA b
ПАРАБОЛЫ
a>0
a
ПО ЕЕ ЭСКИЗУ
y
x1
x0
x2
c 0
y0
b=-a(x1+x2)
x
b
c
D
X1
X2
b>0
c=0
D>0
X1<0
X2=0
СЛЕДСТВИЕ ИЗ
ТЕОРЕМЫ ВИЕТА

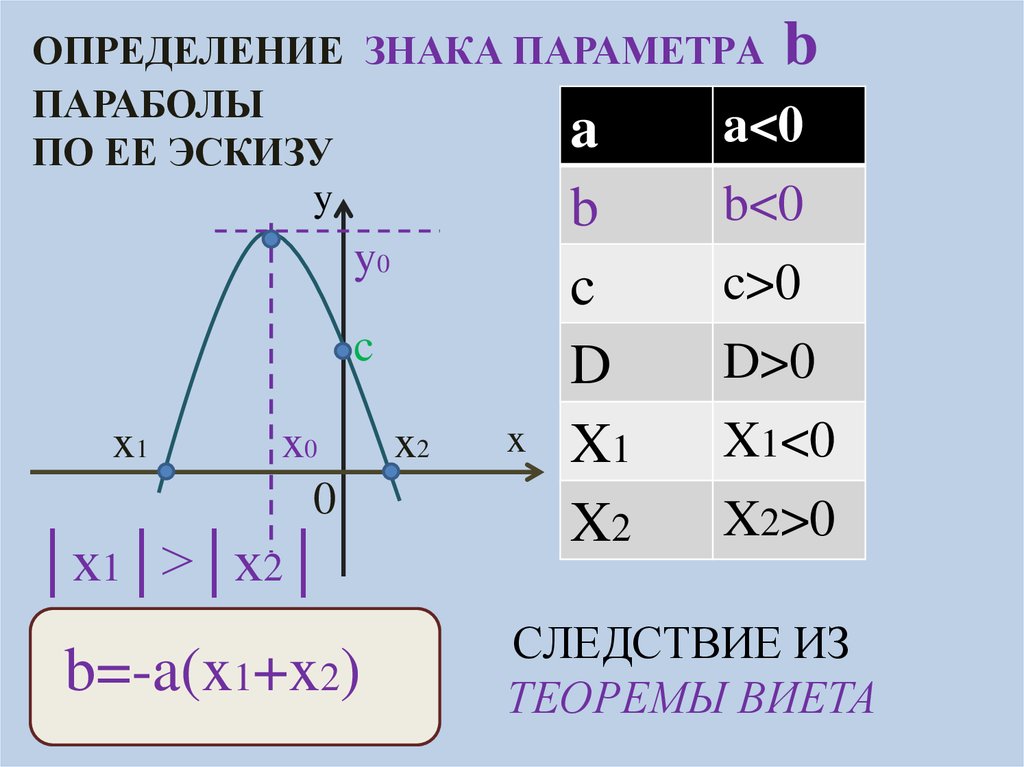
14.

ОПРЕДЕЛЕНИЕ ЗНАКА ПАРАМЕТРA b
ПАРАБОЛЫ
a<0
a
ПО ЕЕ ЭСКИЗУ
y
b<0
b
y0
c
x1
x0
0
│x1│>│x2│
b=-a(x1+x2)
x2
x
c
D
X1
X2
c>0
D>0
X1<0
X2>0
СЛЕДСТВИЕ ИЗ
ТЕОРЕМЫ ВИЕТА

15.

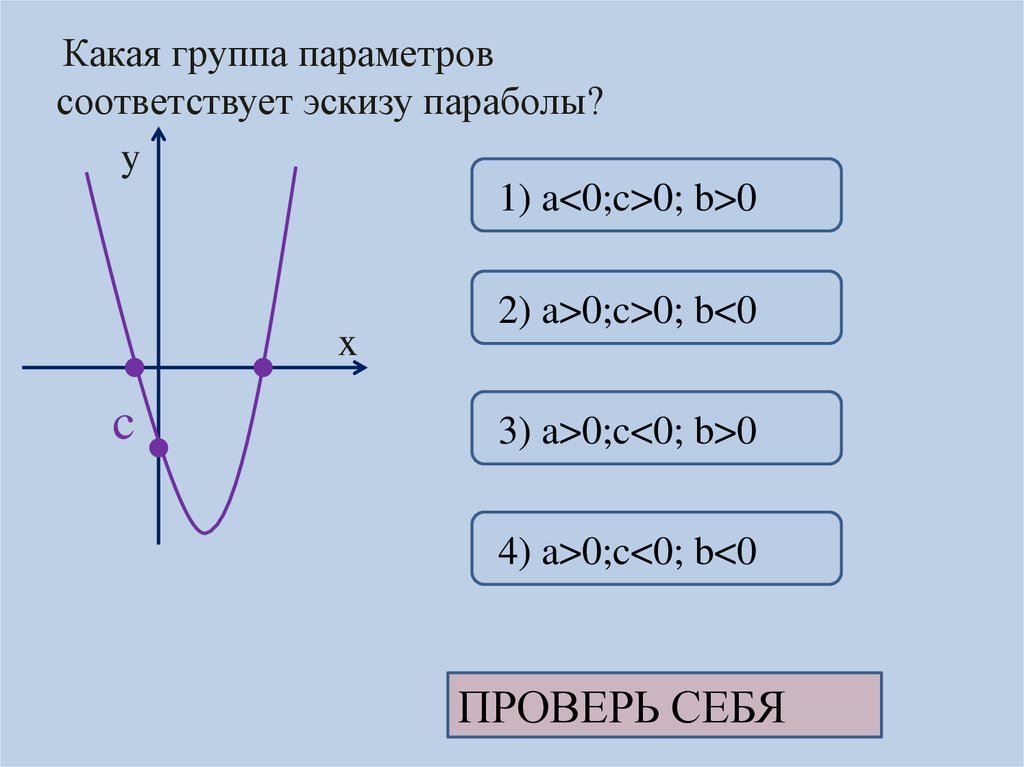
Какая группа параметров
соответствует эскизу параболы?
y
1) a<0;c>0; b>0
x
c
2) a>0;c>0; b<0
3) a>0;c<0; b>0
4) a>0;c<0; b<0
ПРОВЕРЬ СЕБЯ

16.

Определить значение параметров
графикам функций.
y
m и p по
2
y= -x +2mx;
A: x1=0;
B:x2=2m; =>m=x2/2
x2=3;=>m=1,5.
2
4
C
x
A
y= 3px; => C: x=2; y=4;
ветви направлены вверх
2
=>p>0;=> p= y/3x ;=>p=1/3.
2 B

17.

Какая группа параметров
соответствует эскизу параболы?
y
x
1) a<0;c>0; D>0
2) a<0;c<0; D<0
3) a<0;c>0; D<0
c
4) a>0;c<0; D>0
ПРОВЕРЬ СЕБЯ

18.

Определить значение параметров b и k,
восстановить уравнение параболы:
y= x2- (b-5)x -k, при x1=-6 ; x2=4.
□xo=(x1+x2)/2;
x0=(-6+4)/2=-1;
(b-5)/2=-1; b=3;
k=x1 x2= -24;
2
y= x +2x-24.■
1)b=7; k=-2
2)b=-7; k=24
3)b=-3; k=-24
4) b=3; k=-24
ПРОВЕРЬ СЕБЯ

19.

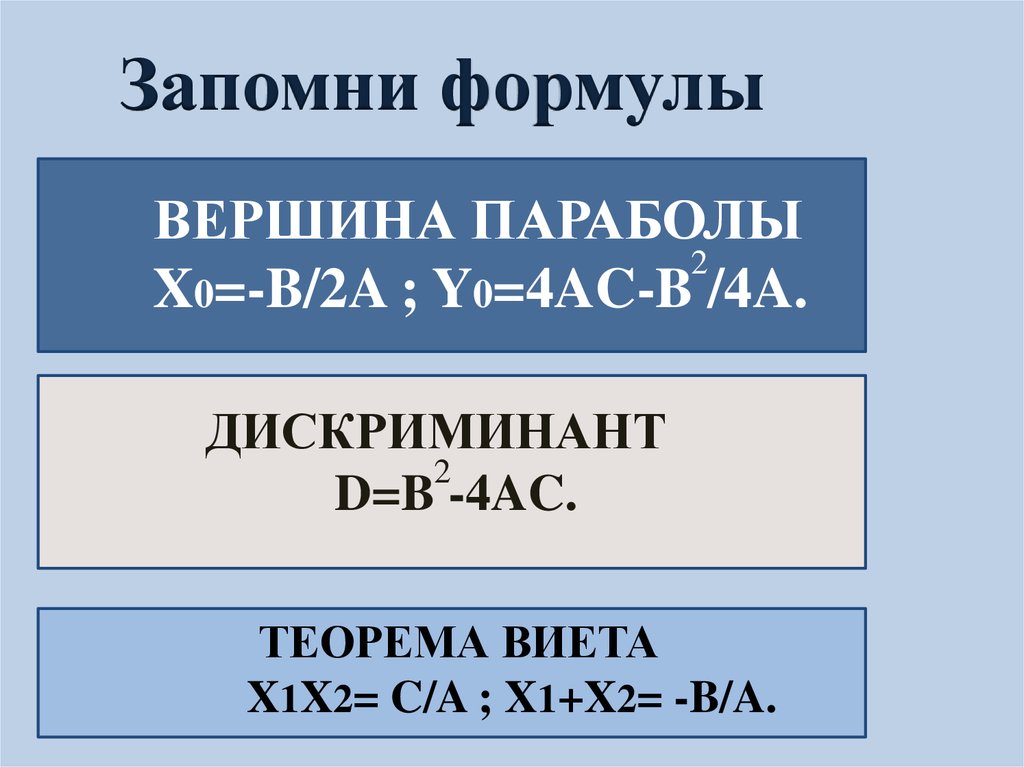
Запомни формулы
ВЕРШИНА ПАРАБОЛЫ
2
X0=-B/2A ; Y0=4AC-B /4A.
ДИСКРИМИНАНТ
2
D=B -4AC.
ТЕОРЕМА ВИЕТА
X1X2= C/A ; X1+X2= -B/A.

20.

Интернет-ресурсы
http://im4-tub.yandex.net/i?id=66526120&tov=4&n=2 книга
http://officeimages.microsoft.com/i/1049/TT/01069/01069064.gif
шаблон презентации лист тетради в клетку
Список литературы
•Лысенко Ф.Ф., Калашников В.Ю. и др. Алгебра 9 класс.
Пособие для самостоятельной подготовки к ИА 2006.
Ростов-на-Дону; изд-во «Легион»; 224с.;2005 ISBN 5902806-14-3
• Шестаков С.А. Сборник задач для подготовки к
письменному экзамену за курс основной школы: 9
класс./Шестаков С.А., Высоцкий И.Р., Звавич Л.И./,- 2-е
изд. испр.- М.: АСТ: Астрель, 2006.- 255с. ISBN 5-27112877-6