Числовые характеристики ССВ. (Лекция 8)

1. Числовые характеристики ССВ

Начальные моменты
r
mr ,s M X Y
s
Центральные моменты
r ,s M
X Y
r
s

2. Начальные моменты

r
mr ,s M X Y
ДСВ
r
i
x
i
s
НСВ
s
k
y pik
r s
x
y f x, y dx dy
k
m2,0 M X 2Y 0 m2 X
m1,0 M X 1Y 0 M X
m0,1 M X 0Y 1 M Y
m0,2 M X 0Y 2 m2 Y
1 1
m1,1 M X Y M XY

3. Центральные моменты

X X mX
r ,s M
X Y
r
s
Y Y mY
ДСВ
НСВ
r y m s p
x
m
i
k
ik
X
Y
r
s
x
m
y
m
f x, y dx dy
X
Y
i k
D
1,0 M X m X 0
2 , 0 M X m X
0,1 M Y mY 0
2
X
0, 2 M Y m Y DY
2
1,1 M X 1 Y 1 M X m X Y mY

4. Ковариация

M X m Y m
1,1 M X
1Y1
X
Y
соv ( X , Y )
Теорема 1 Если СВ X и Y независимы, то
соv ( X , Y ) 0
Доказательство. СВ X и Y независимы
f x , y f X x f Y y
соv ( X , Y )
x m X y mY f x, y dx dy
x m X y mY f X x f Y y dx dy

5. Ковариация

M X m Y m
1,1 M X
1Y1
X
соv ( X , Y )
Y
Теорема 1 Если СВ X и Y независимы, то
соv ( X , Y ) 0
Доказательство
соv ( X , Y )
x m X f X x dx y mY f Y y dy
M X m X M Y mY 0

6. Вычисление ковариации

соv ( X , Y ) M X m Y m
X
Y
M XY m X Y Xm Y m X m Y
M XY m X m Y
соv( X ,Y ) M XY m X m Y

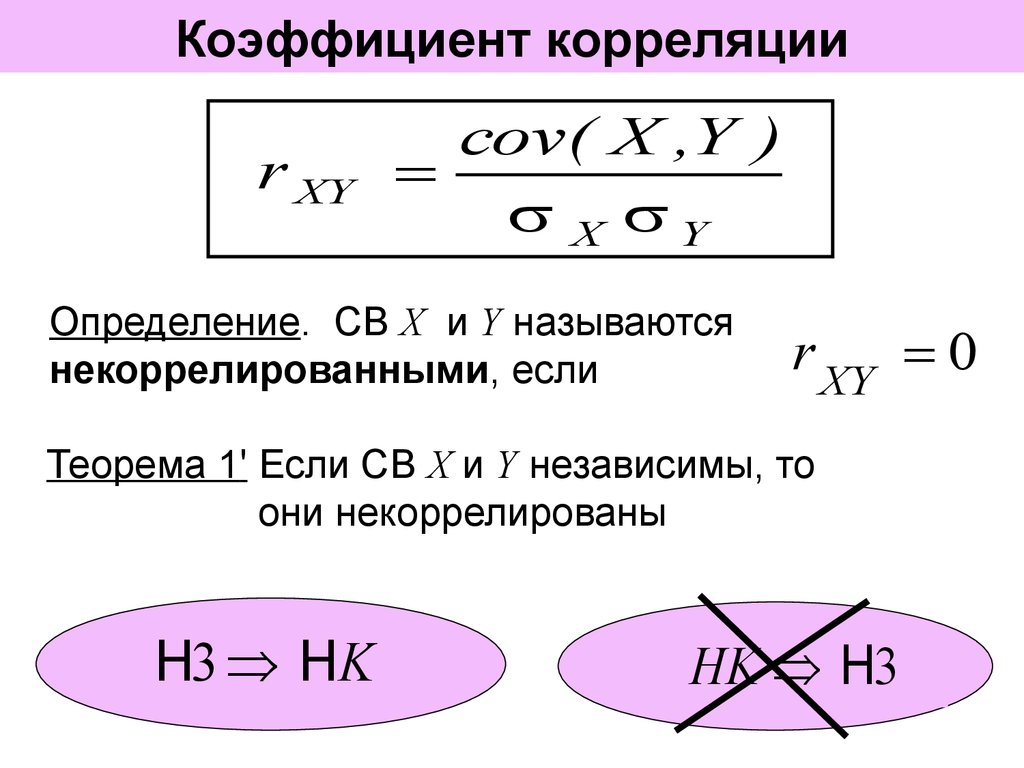
7. Коэффициент корреляции

r XY
соv( X ,Y )
X Y
Определение. СВ X и Y называются
некоррелированными, если
r XY 0
Теорема 1' Если СВ X и Y независимы, то
они некоррелированы
H3 HK
HK H3

8. Свойства математического ожидания

М1
M a bX a bM X
М2
M X Y M X M Y
М3
M XY m X mY соv ( X , Y )
Следствие из М3. Если X и Y некоррелированы, то
M XY m X m Y

9. Свойства дисперсии

2
Д1
D(a bX ) b D X
Д2
D X Y D X D Y 2соv ( X , Y )
Д3
Если X и Y независимы, то
2
2
X
Y
D XY D X D Y m D Y m D X
Следствие из Д2. Если X и Y некоррелированы, то
D X Y D X D Y

10. Доказательство свойства Д2

Д2
D X Y D X D Y 2соv ( X , Y )
X Y M X Y
M X M X Y M Y
2
D X Y M
2
2
2
M X 2 X Y Y
M X Y
2
2
M X
2 M X Y M Y
D X 2соv( X ,Y ) D Y
2

11. Свойства коэффициента корреляции

r XY
К1
К2
К3
соv( X ,Y )
X Y
Если X и Y независимы, то
r XY 0
r XY 1
Y a bX r
XY
1, b 0
1, b 0

12. Доказательство свойства К2

r XY 1
К2
*
*
M X 0 X 1
* *
cov X ,Y r XY
* *
*
*
* *
D X Y D X D Y 2cov X ,Y
X mX
X
X
*
2 1 r XY 0
1 r XY 0
1 r XY 0
r XY 1
r XY 1

13. Доказательство свойства К3

К3 Покажем,что
Y a bX
M Y a bM X
1, b 0
rXY
1, b 0
2
D Y b D X
cov( X , Y ) M ( X m X Y mY )
r
D X DY
DX DY
XY
2
b M ( X m X ) b D X
b
2
b D X b
D X b D X

14. Доказательство свойства К3

К3
Покажем,что
rXY 1
Y a bX
*
*
D X Y 2 1 rXY
rXY 1
*
*
D X Y 0 M X
*
*
*
*
*
*
Y с
с M X Y M X M Y 0
* *
X Y 0
Y mY X m X
Y
X
Y mY Y X m X
X

15. Числовые характеристики ССВ

Ковариационная матрица
системы n случайных величин
( X1, X 2 ,..., X n )
m m X , m X ,...m X
1
2
2
1
соv ( X1, X 2 )
2
соv ( X 2 , X1)
2
K
...
...
соv ( X , X ) соv ( X , X )
n 1
n 2
n
... соv ( X1, X n )
... соv ( X 2 , X n )
...
...
2
...
n