Похожие презентации:
Свойство медиан треугольника
1.
2.
3. В тетради
1. Начертите несколько различныхтреугольников
2. Проведите медианы в этих треугольниках
3. Сделайте вывод.
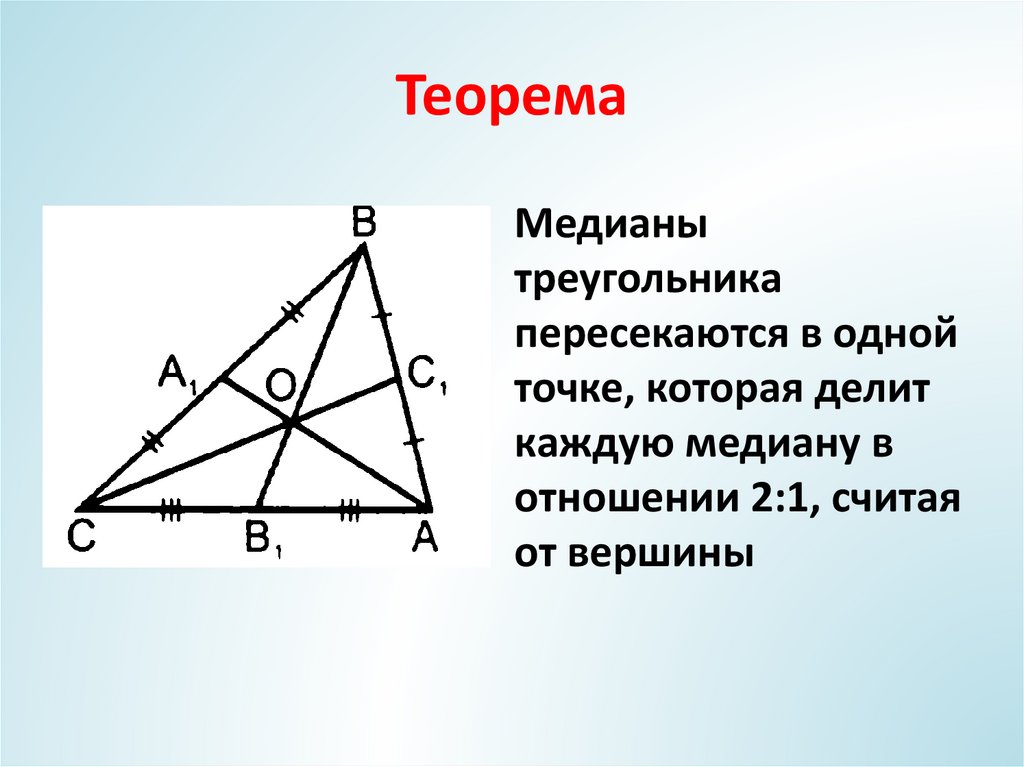
4. Теорема
Медианытреугольника
пересекаются в одной
точке, которая делит
каждую медиану в
отношении 2:1, считая
от вершины
5.
41
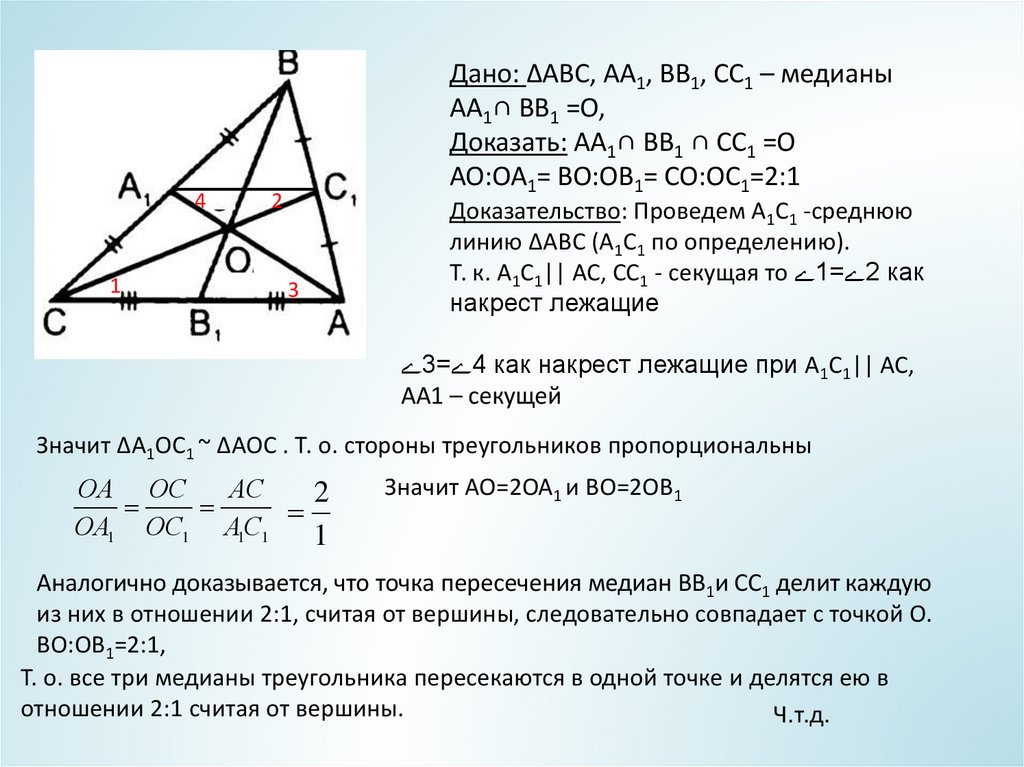
Дано: ΔABC, АА1, ВВ1, СС1 – медианы
АА1∩ ВВ1 =О,
Доказать: АА1∩ ВВ1 ∩ СС1 =О
АО:ОА1= ВО:ОВ1= СО:ОС1=2:1
2
3
Доказательство: Проведем А1С1 -среднюю
линию ΔABC (А1С1 по определению).
Т. к. А1С1|| АС, СС1 - секущая то ے1=ے2 как
накрест лежащие
ے3=ے4 как накрест лежащие при А1С1|| АС,
АА1 – секущей
Значит ΔA1ОC1 ~ ΔAОC . Т. о. стороны треугольников пропорциональны
ОА ОС
АС
2
ОА1 ОС1 А1С1
1
Значит АО=2ОА1 и ВО=2ОВ1
Аналогично доказывается, что точка пересечения медиан ВВ1и СС1 делит каждую
из них в отношении 2:1, считая от вершины, следовательно совпадает с точкой О.
ВО:ОВ1=2:1,
Т. о. все три медианы треугольника пересекаются в одной точке и делятся ею в
отношении 2:1 считая от вершины.
Ч.т.д.



 Математика
Математика








