Соотношения между сторонами и углами в треугольнике

2.

О
Дано : МОС ,
1
К СМ , МО МК
Доказать : 1 3;
3
С
МОС 3
2
К
Угол 2 – внешний угол
треугольника СОК при вершине К
М
МОС 1
МОС 2
1 2
2 3 СОК
2 3
МОС 2
МОС 3
2
3

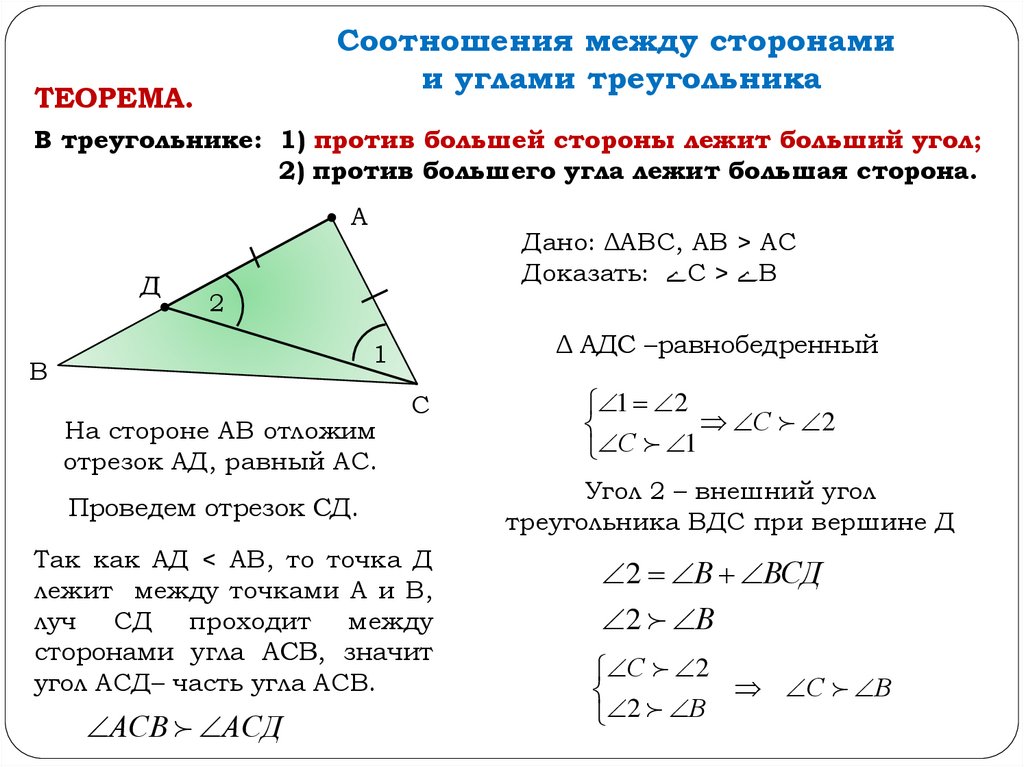
Соотношения между сторонами
и углами треугольника
ТЕОРЕМА.
В треугольнике: 1) против большей стороны лежит больший угол;
2) против большего угла лежит большая сторона.
А
Дано: ΔАВС, АВ > АС
Доказать: ‫ے‬С > ‫ے‬В
2
Δ АДС –равнобедренный
1
В
На стороне АВ отложим
отрезок АД, равный АС.
С
Проведем отрезок СД.
Так как АД < АВ, то точка Д
лежит между точками А и В,
луч СД проходит между
сторонами угла АСВ, значит
угол АСД– часть угла АСВ.
АСВ АСД
1 2
С 2
С 1
Угол 2 – внешний угол
треугольника ВДС при вершине Д
2 В ВСД
2 В
С 2
С В
2
В

4.

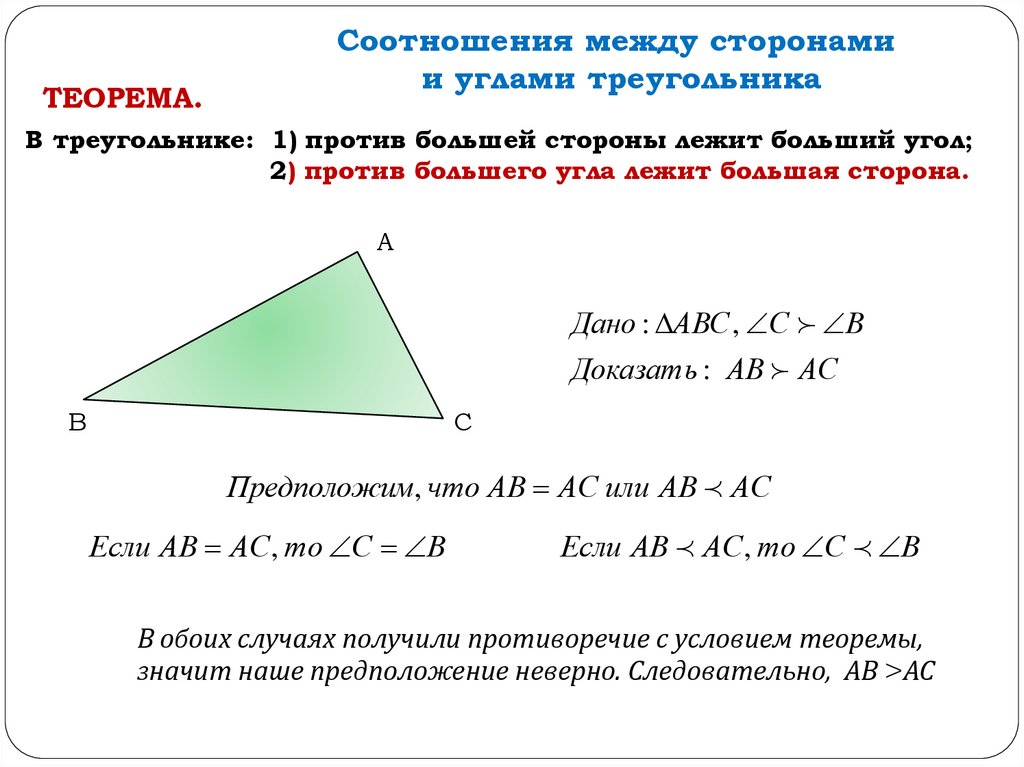
ТЕОРЕМА.
Соотношения между сторонами
и углами треугольника
В треугольнике: 1) против большей стороны лежит больший угол;
2) против большего угла лежит большая сторона.
А
Дано : АВС , С В
Доказать : АВ АС
В
С
Предположим, что АВ АС или АВ АС
Если АВ АС, то С В
Если АВ АС, то С В
В обоих случаях получили противоречие с условием теоремы,
значит наше предположение неверно. Следовательно, АВ >АС

5.

Соотношения между сторонами
и углами треугольника
СЛЕДСТВИЕ 1.
А
В
С
В прямоугольном
треугольнике
гипотенуза больше
катета
Почему ?
СЛЕДСТВИЕ 2. (признак равнобедренного треугольника)
В
Если два угла
треугольника равны,
то треугольник
равнобедренный
Почему ?
А
С

6.

Неравенство треугольника
Каждая сторона треугольника
меньше суммы двух других сторон
ТЕОРЕМА.
В
Дано : АВС
1
Доказать : АВ АС СВ
2
А
С
Д
На продолжении стороны
АС отложим отрезок СД,
равный ВС
Рассмотрим треугольник АВД
1 2
АВД 2
АВД 1
АВ АС СД
Д В
АВ АД
АВ АС ВС

7.

Неравенство треугольника
№ 251. Докажите, что каждая сторона треугольника больше
разности двух других сторон
В
Дано : АВС
Доказать : АВ АС СВ
АВ ВС АС
А
С
АВ АС ВС
АС ВС АВ АС ВС
АВ ВС АС АВ ВС
АВ АС ВС АВ АС

8.

Среди данных треугольников найди не существующие:
Р
А
5
9
5
3
К
В
С
4
15
X
Р
М
18
G
13
A
Z
6
2
12
N
W
Y
9
3
4
О
R
7
2 С
T
6
8
7
5
F
V
11
E

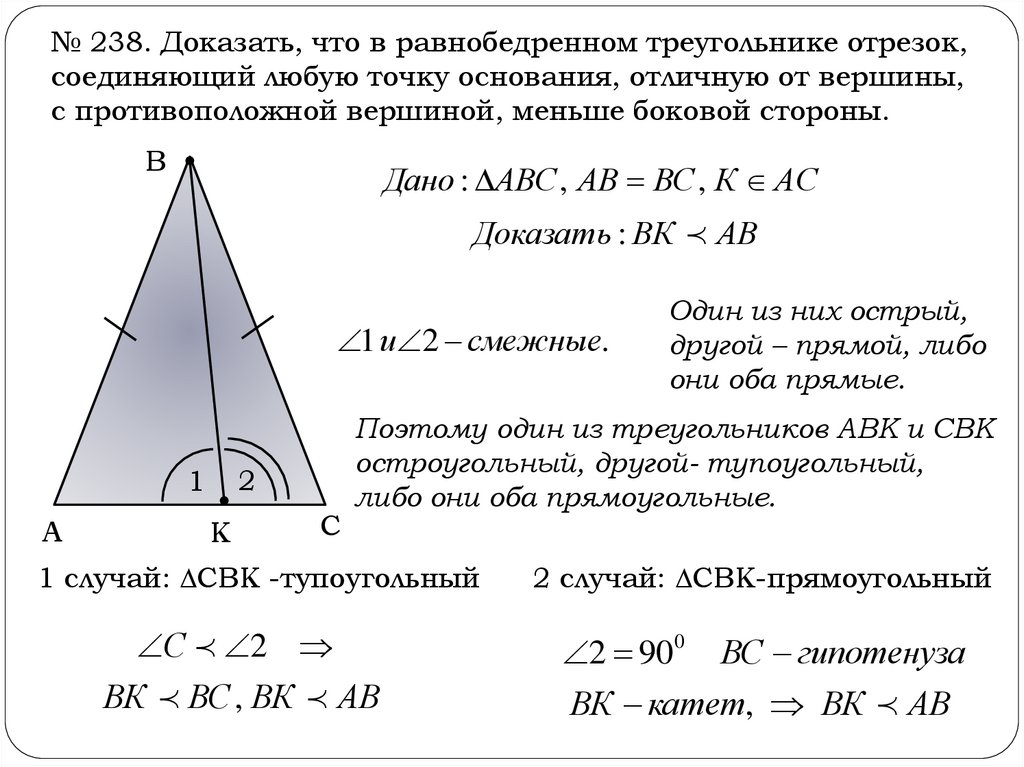
9.

№ 238. Доказать, что в равнобедренном треугольнике отрезок,
соединяющий любую точку основания, отличную от вершины,
с противоположной вершиной, меньше боковой стороны.
В
Дано : АВС , АВ ВС , К АС
Доказать : ВК АВ
1 и 2 смежные.
2
1
А
К
С
Один из них острый,
другой – прямой, либо
они оба прямые.
Поэтому один из треугольников АВК и СВК
остроугольный, другой- тупоугольный,
либо они оба прямоугольные.
1 случай: СВК -тупоугольный
С 2
ВК ВС , ВК АВ
2 случай: СВК-прямоугольный
2 900
ВС гипотенуза
ВК катет, ВК АВ

10.

Дано : АВС ,
№ 239. Доказать, что в
треугольнике медиана не
меньше высоты, проведенной
из
той
же
вершины.
АМ МС ( ВМ медиана ),
ВН АС ( ВН высота).
Доказать : ВМ ВН
В
1 случай
А
М(Н)
ВМ=ВН (Почему?)
В
2 случай
С
А
М
Н
ВМ>ВН (Почему?)
С

11.

№ 240. В равнобедренном
треугольнике АВС с основанием АС биссектрисы
углов А и С пересекаются
в точке О. Доказать, что
АОС - равнобедренный
Дано : АВС , АВ ВС ,
АК биссектриса угла А ( 1 2),
СМ биссектриса угла С ( 3 4),
О АК СМ
Доказать : АОС равнобндренный
В
М
А С
1
1
2
А
2
1
3
4
С
2
К
О
1
3
2
А
2 4
4
С
АОС равнобедренный

12.

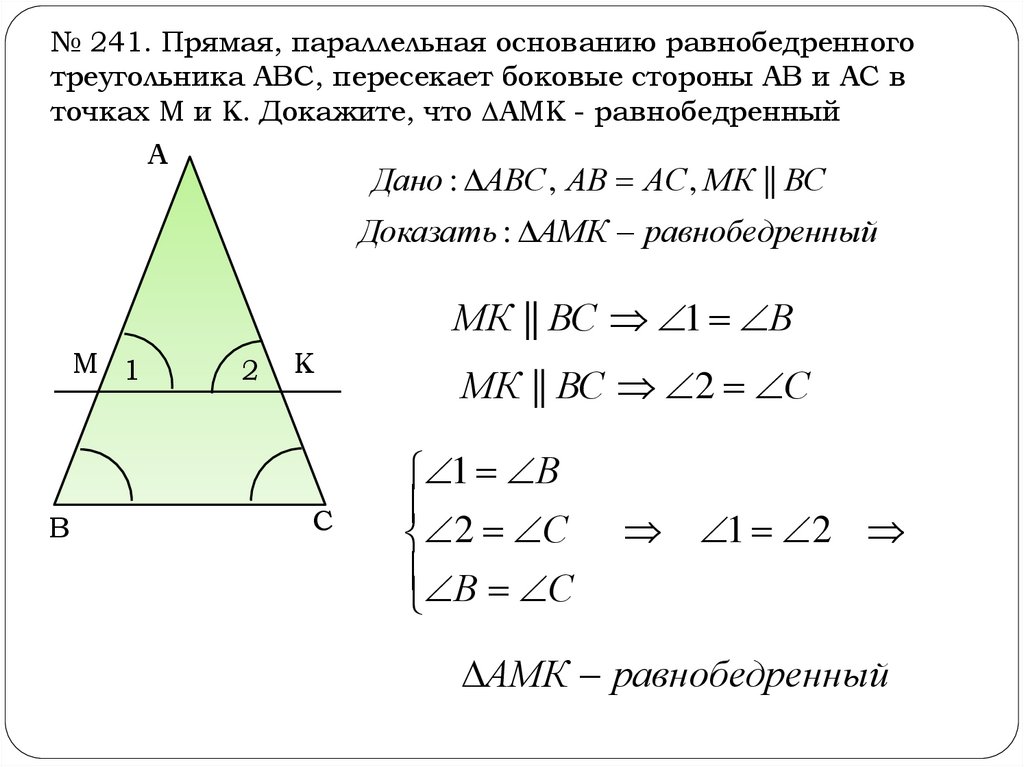
№ 241. Прямая, параллельная основанию равнобедренного
треугольника АВС, пересекает боковые стороны АВ и АС в
точках М и К. Докажите, что АМК - равнобедренный
А
Дано : АВС , АВ АС , МК || ВС
Доказать : АМК равнобедренный
МК || ВС 1 В
М 1
В
2
К
С
МК || ВС 2 С
1 В
2 С
В С
1 2
АМК равнобедренный

13.

№ 242. Докажите, что если биссектриса внешнего угла
треугольника параллельна третьей стороне треугольника, то
треугольник - равнобедренный
К
Дано : АВС , КАС внешний,
АМ биссектриса КАС ( 1 2), АМ || ВС
А
1
М
2
Доказать : АВС равнобедренный
АМ || ВС 1 3 (соответственные)
АМ || ВС 2 4 (накрест лежащие)
3
В
1 2
1 3
2 4
4
С
3 4
АВС равнобедренный

14.

№ 243. Через вершину С треугольника АВС проведена прямая,
параллельная его биссектрисе АК и пересекающая прямую АВ
в точке Д. Докажите, что АС = АД.
В
Дано : АВС ,
АК биссектриса ( 1 2), СД || АК
Доказать : АС АД
К
АК || СД 1 3 (соответственные)
АК || СД 2 4 (накрест лежащие)
1
2
1 2
1 3
2 4
А
4
3
АДС равнобедренный, то есть АС АД
Д
С
3 4

15.

№ 244. Отрезок АД – биссектриса треугольника АВС. Через
точку Д проведена прямая, параллельная АС и пересекающая
сторону АВ в точке Е. Докажите, что Δ АДЕ - равнобедренный.
В
Дано : АВС ,
АД биссектриса ( 1 2), ДЕ || АС
Доказать : АДЕ равнобедренный
Д
Е
3
2
А
1
4
С
ДЕ || АС 1 3 (накрест лежащие)
АДЕ равнобедренный

16.

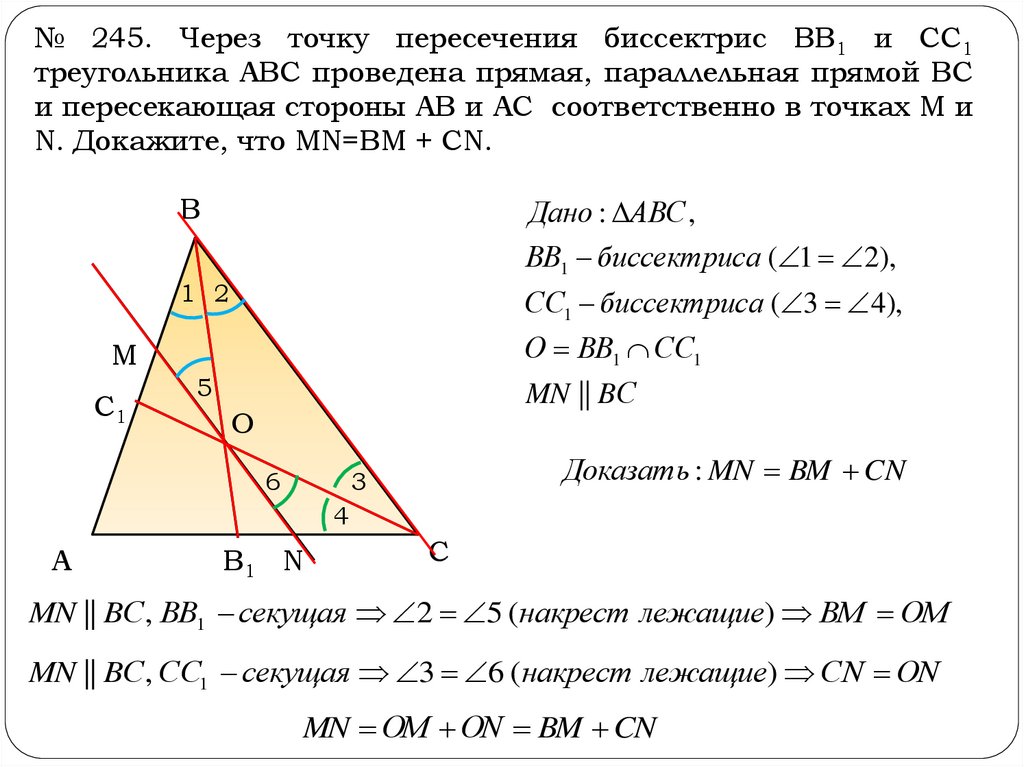
№ 245. Через точку пересечения биссектрис ВB1 и СC1
треугольника АВС проведена прямая, параллельная прямой ВС
и пересекающая стороны АВ и АС соответственно в точках М и
N. Докажите, что MN=BM + CN.
В
Дано : АВС ,
ВВ1 биссектриса ( 1 2),
1 2
СС1 биссектриса ( 3 4),
О ВВ1 СС1
M
C1
5
MN || BС
O
6
Доказать : MN BM CN
3
4
А
B1 N
С
MN || BС, ВВ1 секущая 2 5 (накрест лежащие) ВМ ОМ
MN || BС, СС1 секущая 3 6 (накрест лежащие) СN ОN
MN ОМ ОN BM CN

17.

№ 246. На рисунке ВО и СО – биссектрисы углов В и С
треугольника АВС. OE || AB, OD||AC. Доказать, что периметр
треугольника ЕDО равен длине отрезка ВС.
А
Дано : АВС ,
ВО биссектриса ( 1 2),
СО биссектриса ( 3 4),
O
1
В
5
ОЕ || АВ, ОD || АC
6
2
4
Е
D
Доказать : РЕDO BC
3
С
АВ || ОЕ , ВО секущая 1 5 (накрест лежащие) ВЕ ОЕ
АС || ОD , OC секущая 3 6 (накрест лежащие) OD DC
PEDO OE ED OD BE ED DC BC

18.

№ 247. На рисунке АВ=АС, AP=AQ. Доказать, что: а) Δ ВОС равнобедренный;
б) Прямая ОА проходит через середину
основания ВС и перпендикулярна к нему.
А
Дано : АВС , AB AC , AP AQ
Доказать :
3 4
а) BOC равнобедренный;
б ) ВК КС , АО ВС
Р
Q
BCP QBС (Почему ?)
O
1 2 ВОС равнобедренный
1
В
ABO ACO (Почему ?)
2
К
С
3 4 AK биссектриса
ABС равнобедренный, АК биссектриса, а значит...

English Русский Правила