Тригонометриялық функциялар

1.

2.

1. Оқушылардың “тригонометриялық функциялар”
тарауы бойынша білімдерін ж8йелеу.
2. Оқушылардың танымдық, шығармашылық ізденістерін арттыру.
3. Оқушыларды еңбекке, ұқыптылыққа, жауапкершілікке тәрбиелеу.

3.

1.” Архижинақтаушы” тобы
2.“Ізденушілер” тобы
3.“Теорияшылар ” тобы
4.“Есеп шығарушылар” тобы
5.“Сарапшылар” тобы

4.

“Архижинақтаушы” тобы

5. Бернулли Иоганн (1667-1748 ж.ж) – швейцария математигі. Ол өзінің серіктесі Лейбницпен бірге «тригонометриялық қатарлар»

теориясымен шұғылданған.
Ол өз еңбектерінде І-ші диф-ференциалдық
теңдеулердің шешу әдістерін, геодезиялық
сызықтар туралы есептің классикалық
анықтамасын және бұл сызық-тардың
геометриялық мағынасын, кейінірек
олардың дифферен-циалдық теңдеулерге
келтіру жолдарын ашты.

6.

• Лобачевский Николай Иванович
( 1792-1856) – орыс математигі. Ол
жоғары дәрежелі алгебралық
теңдеулердің жуық шешімдерін
табу әдісін ашты, сонымен қатар
“анықтауыштар” теориясына көп
еңбегін сіңірді.Н.И.Лобачевский
”тригонометриялық қатарлар”
теориясын терең меңгеріп, жаңа
жетістіктерге қол жеткізген.

7.

Ньютон Исаак (1643-1727)ағылшын астрономы, физигі, әрі
математигі.ХVII ғасырда дифференциалдық және интегралдық
есептеулердің жасалуымен жарыса
математикалық практикаға
шектеусіз қатарларды енгізеді. Ондық
бөлшектер туралы ілімнің
принциптерін қолдана отырып,
дәрежелік қатарларды бөлудің және
қатарлардан түбірлер табудың тура
әдісін табады. Әр түрлі өрнектерді
тригономет-риялық қатарларға
жіктеп, олардың қолдану өрісін едәуір
кеңейтеді.

8.

Эйлер Леонард ( 1707-1783) –
астроном, механик, физик, математик.
Ол швейцарияда туылған. Петербургте
Ғылым Академиясында 30 жылдан
астам қызмет істеген. Шектеусіз
қатар-ларға арналған Эйлердің тамаша
еңбектерінің сериясы 1730 жылдан
басталады. 850 мақалаларын жазып,
көптеген жетістік-терге жетеді.
Атап айтсақ, Эйлер І рет
көрсеткіштік және логарифм-дік
қатарларды қорытып шығарады. Дәл
осы жолмен cosnz және sinnz үшін
қатарлар шығарып алады. Сонымен
қатар, 1/ sinz және ctgz-ң жай
бөлшектерге жіктелуінде Эйлер
тапқан.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

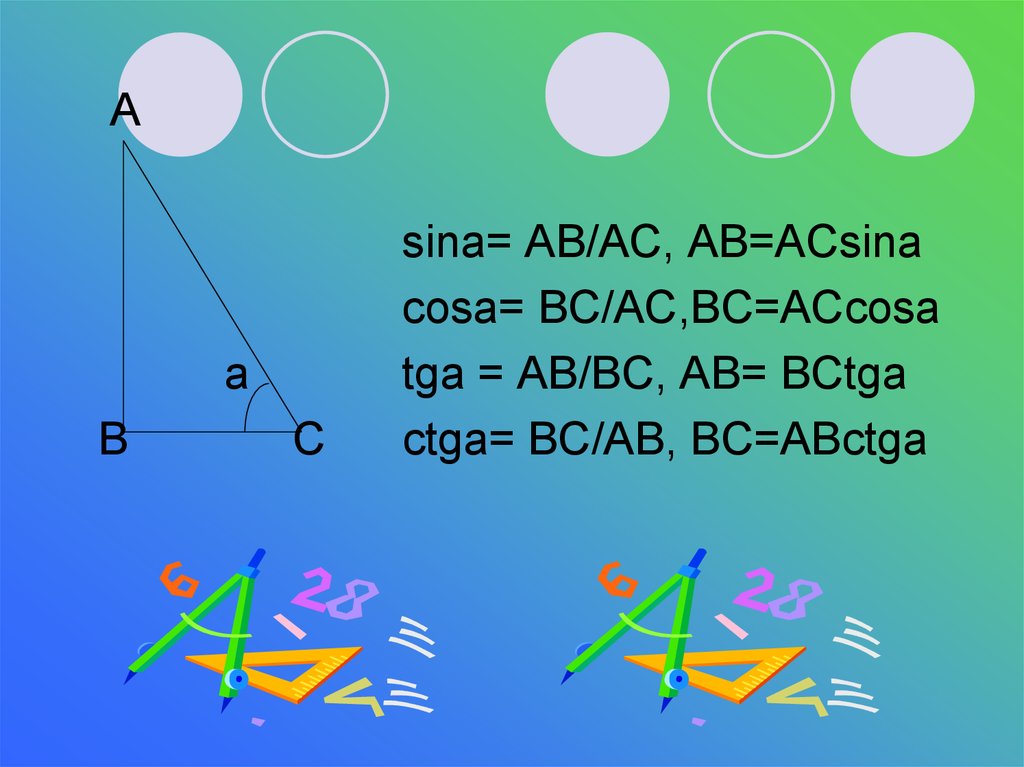
А
a
В
С
sina= AB/AC, AB=ACsina
cosa= BC/AC,BC=ACcosa
tga = AB/BC, AB= BCtga
ctga= BC/AB, BC=ABctga

19.

20.

21.

22.

23.

“Теорияшылар”
тобы

24.

25.

26.

27.

28.

sinx+siny =
cosx+cosy
=
tgx*tgy=
ctgx+ctgy= sinx*cosy=
tgx-tgy=

29.

sinx=a
cosx=a
tgx=a
ctgx=a

30.

31.

y cos( 2 x)
6

32.

2
sin x
y 2
x 1

33.

2
2
3
4 arcsin( ) 8 arccos( ) 15arctg
2
2
3

34.

sin( 60 )
0
4 sin( 15
0
4
) sin( 75
0
4
)

35.

x
x
2
cos cos sin sin
2
5
2
5
2
2 cos2x +cosx -1 =0

36.

sin x sin x
1
tg
2
x
cos
x
3
2
sin x cos sin x 2
4
2
2 sin 4х sin 2x cos 6x cos 2x

37.

7
sin 20
20
0