Похожие презентации:
Қарапайым тригонометриялық теңдеулер
1.
Қарапайымтригонометриялық
теңдеулер
Какеша Есилжан,
2.
Сабақтыңмақсаты:
Қарапайым тригонометриялық
теңдеулер туралы түсінік беріп,
олардың шешімін, дербес жағдайдағы
шешімін табатын есептер шығаруға
үйрету
3.
Қарапайым тригонометриялық теңдеулер дептөмендегі түрдегі теңдеулерді айтамыз:
sin x a
cos x a
tgx a
ctgx a
мұндағы x – белгісіз
айнымалы, a R.
4.
График бойынша sinx=a теңдеуінің шешімін қарастырайық. Ол үшін бізге y=aтүзуі мен y=sinx синусоиданың қиылысу нүктелерінің абсциссаларын табуымыз
керек. Ендеше синусоида салайық.
y
y=a, a>1
a
Масштаб :3
1
2
3
2
3
2
2
0
2
2
x
−1
a
y=a, a<–1
I жағдай: a [–1;1]
Байқағанымыздай синусоида мен түзу қиылыспайды, сондықтан бұл жағдайда
теңдеудің шешімі жоқ!
5.
II жағдай: a [–1;1]Бұл жағдайда қиылысу нүктелері шексіз көп, және олардың абсциссалары
төмендегідей анықталады:
2) Бірінші нүктенің абсциссасы синустың a -ға тең сан мәні (бұрыштың радиандық
өлшемі), яғни ол санның мәні arcsina тең болады.
y
Масштаб :3
1
2
3
2
arcsin a arcsin a
2
2
3
2
a
2
0 arcsin a arcsin a
2
x
2
−1
3) Екінші нүктенің [– ; ] аралығына тиісті абсциссасы ( –arcsina) болатынын
көреміз . Оны біз sinx=sin( –x) теңдігін еске алсақ жеткілікті.
4) Басқа барлық қиылысу нүктелердің абсциссалары осы екеуіне 2 n n түріндегі
санды қосып берсек жеткілікті, (y=sinx функциясы периоды 2 ).
6.
Осылайша, мұндай жағдайда барлық шешімдер жиынтығын төмендегідей жазуғаболады:
arcsin a ·2n, n Z;;
x
arcsin a · 2k 1 , k Z/.
y
Масштаб :3
1
3
2
2
arcsin a arcsin a
2
2
3
2
a
2
0 arcsin a arcsin a
2
−1
Немесе, бұл екі шешімді біріктіріп:
x 1 arcsin a m, m Z..
m
2
x
7.
sin x ax ( 1) arcsin a k , k Z
k
Мысал 1:
1
sin x
2
1
x ( 1) arcsin k , k Z
2
k
x ( 1)
k
6
k , k Z
8.
sin x ax ( 1) arcsin a k , k Z
k
Мысал 2: 2 sin x 1 0
1
sin x
2
1
x ( 1) arcsin k , k Z
2
k
x ( 1)
k 1
6
k , k Z
9.
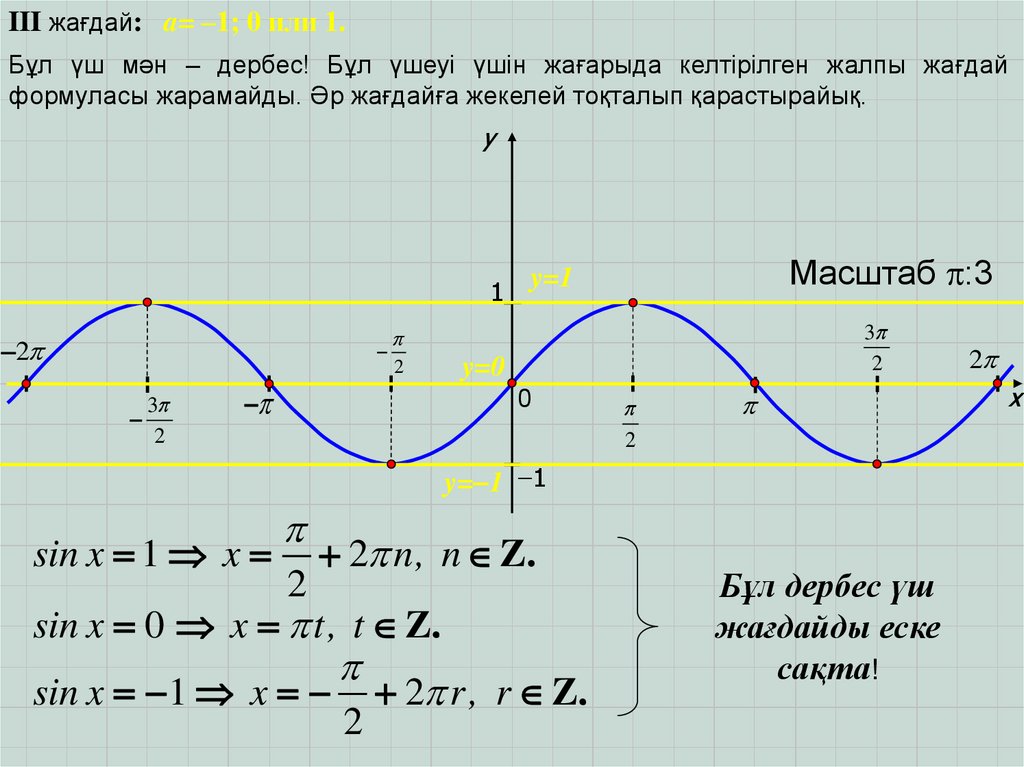
III жағдай: a= –1; 0 или 1.Бұл үш мән – дербес! Бұл үшеуі үшін жағарыда келтірілген жалпы жағдай
формуласы жарамайды. Әр жағдайға жекелей тоқталып қарастырайық.
y
1
2
3
2
Масштаб :3
y=1
3
2
2
y=0
0
2
y=–1 −1
sin x 1 x
2 n, n Z..
2
sin x 0 x t, t Z..
sin x 1 x
2
2 r, r Z..
Бұл дербес үш
жағдайды еске
сақта!
2
x
10.
cosx=a түріндегі теңдеу шешімін де графикалық тәсілмен қарастырайық. Ол үшінy=cos косинусоида және y=a түзуінің қиылысу нүктесінің абсциссаларын
анықтаймыз. x – бойынша косиусоида салайық.
y
y=a, a>1
a
Масштаб :3
1
2
3
2
3
2
2
0
2
−1
a
y=a, a<–1
I жағдай: a [–1;1]
Өткендегідей мұнда да қиылысу нүктесі жоқ, сондықтан шешімі жоқ!
2
x
11.
II жағдай: a [–1;1]Бұл жағдайда қиылысу нүктелері шексіз көп, және олардың абсциссалары
төмендегідей анықталады:
2) Бірінші нүктенің абсциссасы косинустың a - ға тең сан мәні (бұрыштың
радиандық өлшемі), яғни ол санның мәні arccosa - ға тең болады..
1
2
arccos a 2 3
y
Масштаб :3
3
2
2
arccos a 0 arccos a
2
2
x
arccos a 2
2
−1
3) Екінші нүктенің [– ; 0] аралығына тиісті абсциссасы, –arccosa –ға тең. Оны біз
cosx=cos(–x) теңдігінен білеміз.
4) Басқа барлық қиылысу нүктелердің абсциссалары осы екеуіне 2 n n түріндегі
санды қосып берсек жеткілікті.
12.
Осылайша, мұндай жағдайда барлық шешімдер жиынтығын төмендегідей жазуғаболады:
arccos a 2 n, n Z;;
x
arccos a 2 k , k Z/.
1
2
arccos a 2 3
y
Масштаб :3
3
2
2
arccos a 0 arccos a
2
2
−1
Немесе, бұл екі шешімді біріктіріп:
x arccos a 2 m, m Z/.
2
arccos a 2
x
13.
cos x ax arccos a 2 k , k Z
Мысал 3: cos x
2
2
2
x arccos
2 k , k Z
2
x
4
2 k , k Z
14.
Мысал 4:2
cos( 2 x)
2
2
cos 2 x
2
2
2 x arccos
2 k , k Z
2
2x
x
8
4
2 k , k Z
k , k Z
15.
III жағдай: a= –1; 0 или 1.Бұл үш мән – дербес! Бұл үшеуі үшін жағарыда келтірілген жалпы жағдай
формуласы жарамайды. Әр жағдайға жекелей тоқталып қарастырайық.
y
Масштаб :3
1 y=1
2
2
y=0
3
2
0
3
2
2 x
2
y=–1 −1
cos x 1 x 2 n, n Z..
cos x 0 x
t, t Z..
2
cos x 1 x 2 r, r Z..
Бұл дербес үш
жағдайды еске
сақта!
16.
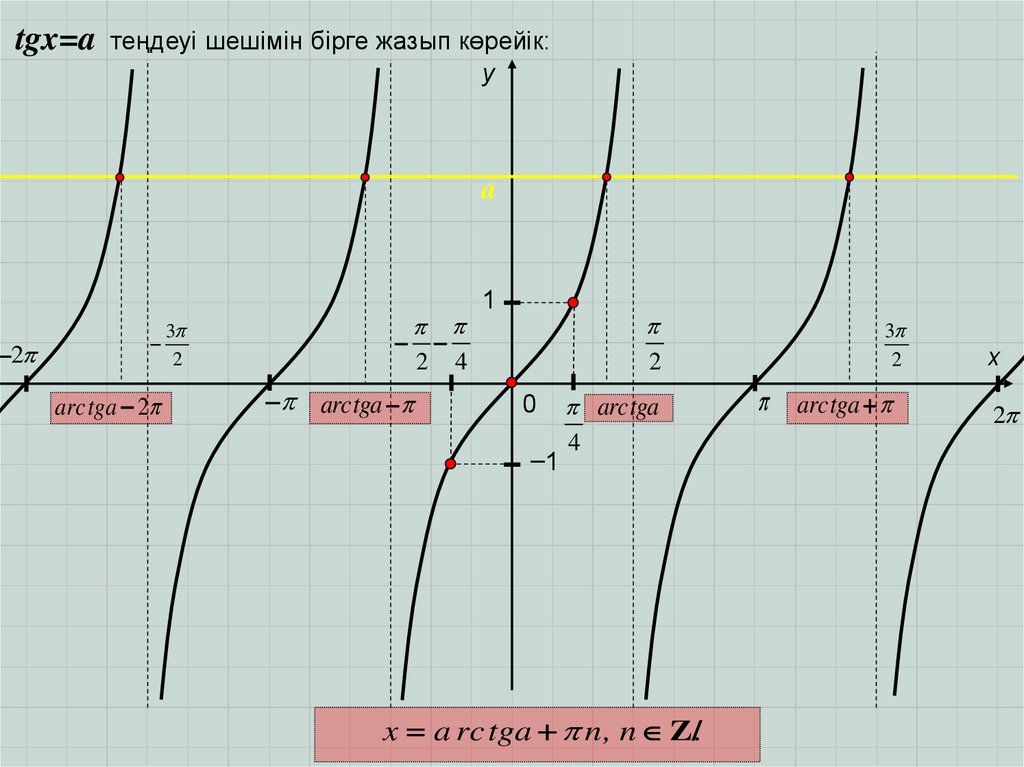
tgx=a теңдеуі шешімін бірге жазып көрейік:2
y
a
arc tga 2
3
2
2 4
arctga
1
0
−1
2
3
2
arctga
4
arctga
x a rc tga n, n Z/.
x
2
17.
сtgx=a теңдеуі шешімін бірге жазып көрейік:y
a
1
2
arc ctga 2
3
2
arcctga
2
0
4
2
3
4
arcctga
−1
Масштаб :3
x a rc ctga n, n Z/.
3
2
arcctga
x
2
18.
ctgx ax arcctga k , k Z
Мысал 5:
x
3
ctg
5
3
x
3
k , k Z
arcctg
5
3
x
k , k Z
5
3
10
x
5 k , k Z
3
19.
20.
Назарларыңызғарахмет!


















 Математика
Математика








