Похожие презентации:
ИГЭС2 семестр Колебания лекция 1
1.
06.04.20191
2. ЛЕКЦИЯ 1 Физика колебаний
ЛЕКЦИЯ 1ФИЗИКА
КОЛЕБАНИЙ
06.04.2019
2
3.
06.04.20193
4.
Механические колебанияКолебательные процессы весьма часто
встречаются в окружающей нас природе
и технике. Значительная часть
механических движений – движение
машин, работающих циклически; почти
все акустические явления; переменный
ток, применяющийся в быту и в
разнообразных технических устройствах,
биение сердца, колебания атомов, смена
времен года, дня и ночи.
06.04.2019
4
5.
06.04.20195
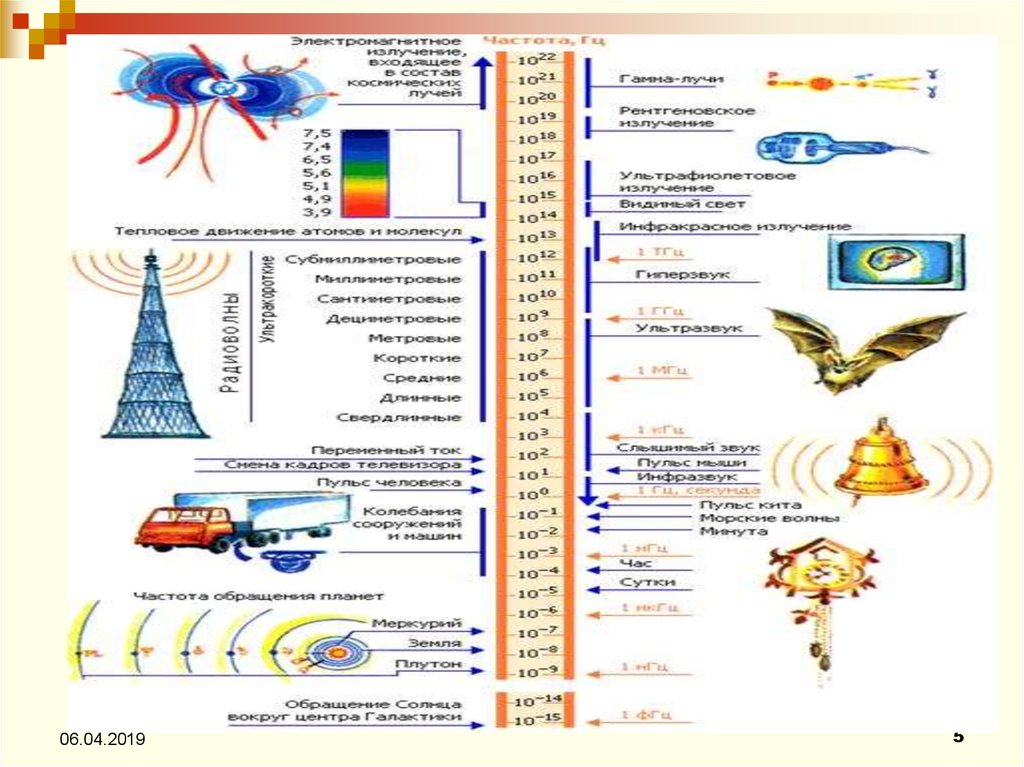
6. Колебания (колебательные движения)- изменения состояния, обладающие той или иной степенью повторяемости во времени.
КОЛЕБАНИЯКолебания (колебательные движения)изменения состояния, обладающие той или
иной степенью повторяемости во времени.
Колебания могут иметь различную физическую
природу, но иметь общие закономерности и
описываться однотипными математическими
методами.
Колебания различают:
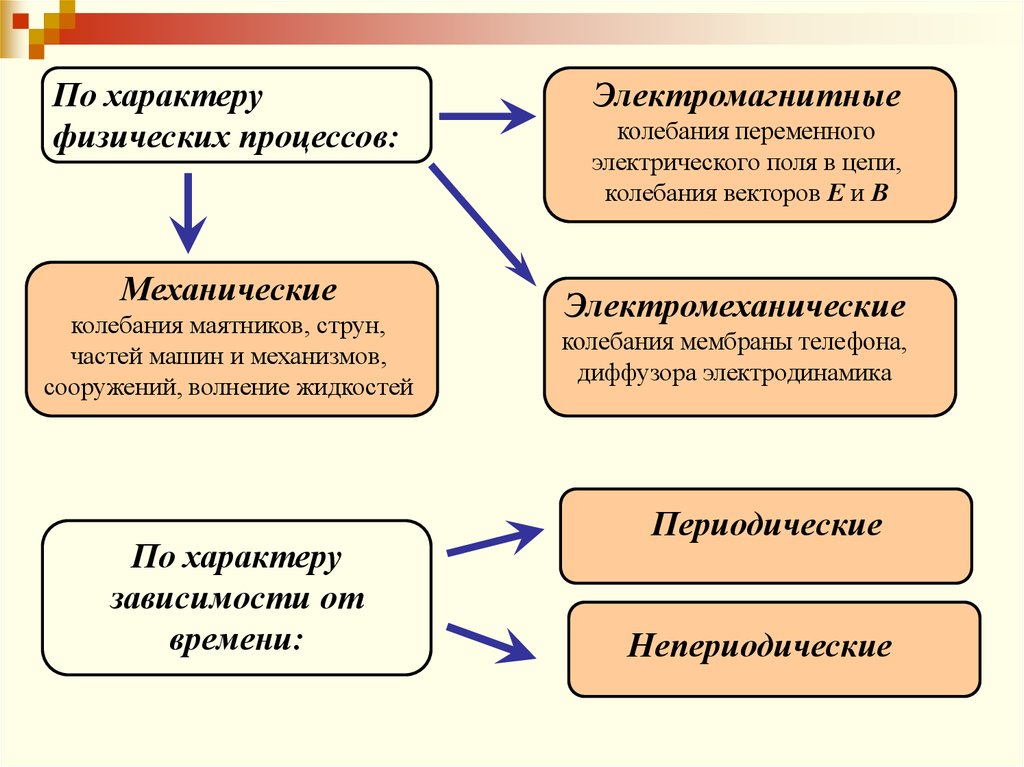
•по характеру физических процессов
•по характеру зависимости от времени.
7.
По характеруфизических процессов:
Механические
колебания маятников, струн,
частей машин и механизмов,
сооружений, волнение жидкостей
По характеру
зависимости от
времени:
Электромагнитные
колебания переменного
электрического поля в цепи,
колебания векторов Е и В
Электромеханические
колебания мембраны телефона,
диффузора электродинамика
Периодические
Непериодические
8.
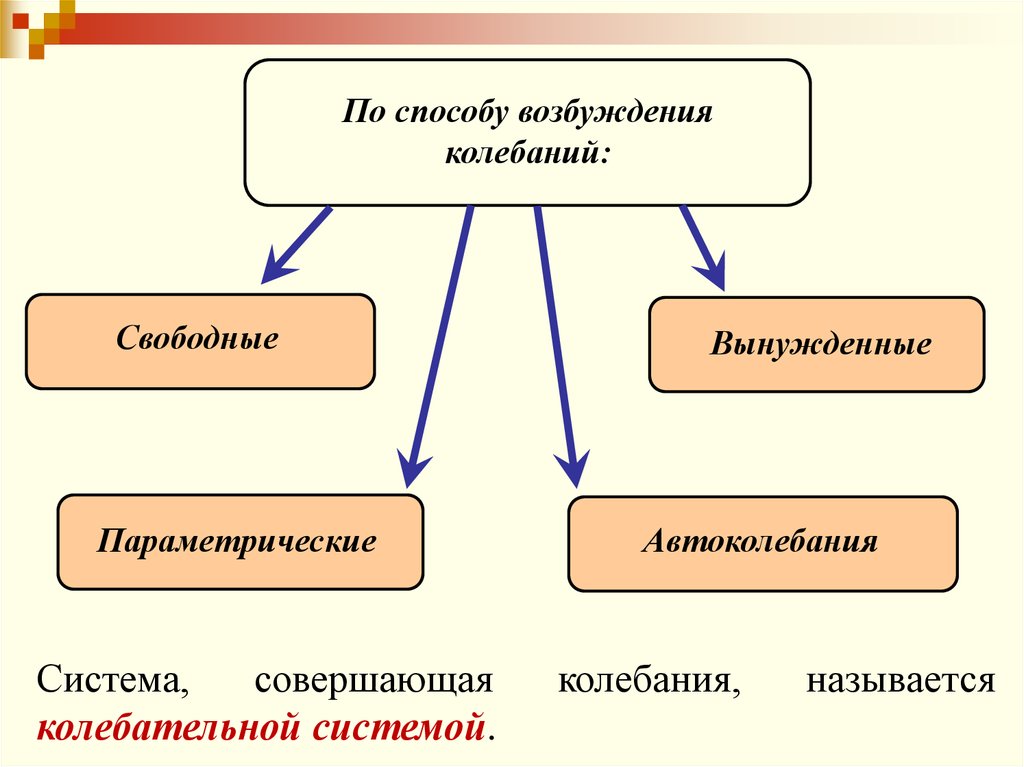
По способу возбужденияколебаний:
Свободные
Параметрические
Система,
совершающая
колебательной системой.
Вынужденные
Автоколебания
колебания,
называется
9. Свободные (или собственные) — это колебания в системе не подверженных действию переменных внешних сил, под действием внутренних
Свободные (или собственные) — этоколебания в системе не подверженных
действию переменных внешних сил, под
действием внутренних сил после того, как
система выведена из состояния
равновесия (в реальных условиях из-за
трения свободные колебания всегда
затухающие). Простейшими примерами
свободных колебаний являются колебания
груза, прикреплённого к пружине, или
груза, подвешенного на нити.
9
10. Условия возникновения свободных колебаний 1. Колебательная система должна иметь положение устойчивого равновесия. 2. При
выведении системы изположения равновесия должна
возникать равнодействующая сила,
возвращающая систему в исходное
положение
3. Силы трения (сопротивления) очень
11.
Параметрические — колебания, возникающие при изменении какого-либо параметраколебательной системы в результате
внешнего воздействия.
Вынужденные — колебания, протекающие в
системе под влиянием внешнего
периодического воздействия. Может
возникнуть явление резонанса: резкое
возрастание амплитуды колебаний при
совпадении собственной частоты
осциллятора и частоты внешнего
воздействия.
06.04.2019
11
12.
Автоколебания — колебания, прикоторых система имеет
запас потенциальной энергии,
расходующейся на совершение колебаний
(пример такой системы — механические
часы). Характерным отличием
автоколебаний от вынужденных
колебаний является то, что их амплитуда
определяется свойствами самой системы,
а не начальными условиями.
06.04.2019
12
13.
Колебания - периодические, еслизначения физических величин,
изменяющихся в процессе
колебаний, повторяются через
равные промежутки времени
06.04.2019
13
14.
Периодические процессы можнопредставить как наложение
гармонических колебаний.
Фурье установил, что любое
периодическое негармоническое
колебание может быть представлено
как сумма гармонических колебаний.
15.
Гармонические колебания –колебания, при которых
колеблющаяся величина
изменяется со временем по
закону синуса или косинуса.
06.04.2019
15
16.
Простейшей моделью гармоническогоколебания является колебание
проекции x конца радиуса-вектора r
точки, движущейся по окружности
радиусом A с постоянной угловой
скоростью ω0. Такое представление
гармонических колебаний называют
векторной диаграммой.
06.04.2019
16
17.
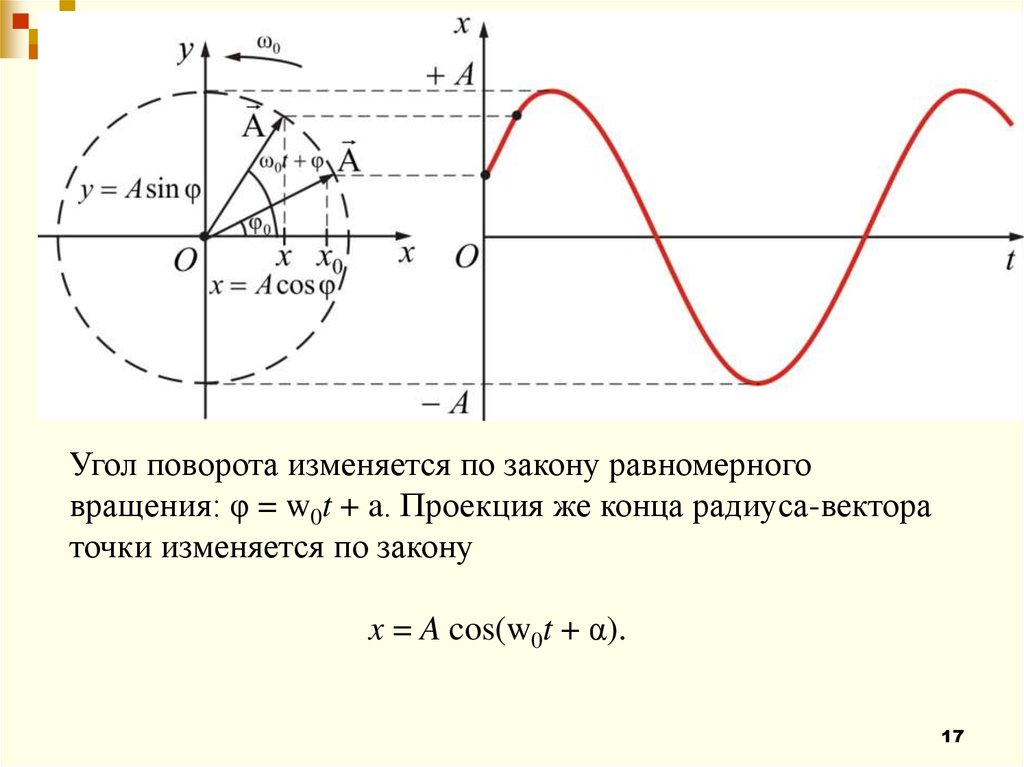
Угол поворота изменяется по закону равномерноговращения: φ = w0t + a. Проекция же конца радиуса-вектора
точки изменяется по закону
x = A cos(w0t + α).
17
18. Если некоторая материальная точка совершает гармоническое колебательное движение около положения равновесия вдоль некоторой оси
x (гармоническийосциллятор), то ее координата меняется
по закону:
x = A cos(ω0t + φ0), где x –смещение из
положения равновесия, A – амплитуда
колебаний, φ0- начальная фаза, ωциклическая частота.
06.04.2019
18
19. Характеристики колебательного движения 1. Амплитуда 2. Период 3. Частота
06.04.201919
20.
Период колебаний - (Т) наименьшийпромежуток времени, через который
повторяются значения всех физических
величин, характеризующих колебательное
движение. Период измеряется в секундах.
Частота периодических колебаний – число
полных колебаний, совершаемых в единицу
времени. Частота колебаний измеряется в
1
герцах.
T
Если за какое-то время t система совершает n
колебаний, то Т= t/n
21.
Амплитуда - Наибольшее (по модулю)отклонение колеблющегося тела от
положения равновесия
Циклическая ( круговая частота)
– число колебаний за 2π секунд
ω=2πν
06.04.2019
21
22. Механические гармонические колебания Гармонические колебания – простейшие периодические колебания, при которых координата тела
Механические гармоническиеколебания
Гармонические колебания – простейшие
периодические колебания, при которых
координата тела меняется по закону синуса
или косинуса
23. Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Рассмотрим прямолинейные гармонические колебания материальной точки вдольоси х около положения равновесия,
совпадающего с началом координат х = 0.
Зависимость координаты х от
времени t задается уравнением
x A cos( t 0 )
24. Кинематика колебаний Циклическая частота связана с линейной частотой и периодом следующими соотношениями
06.04.201924
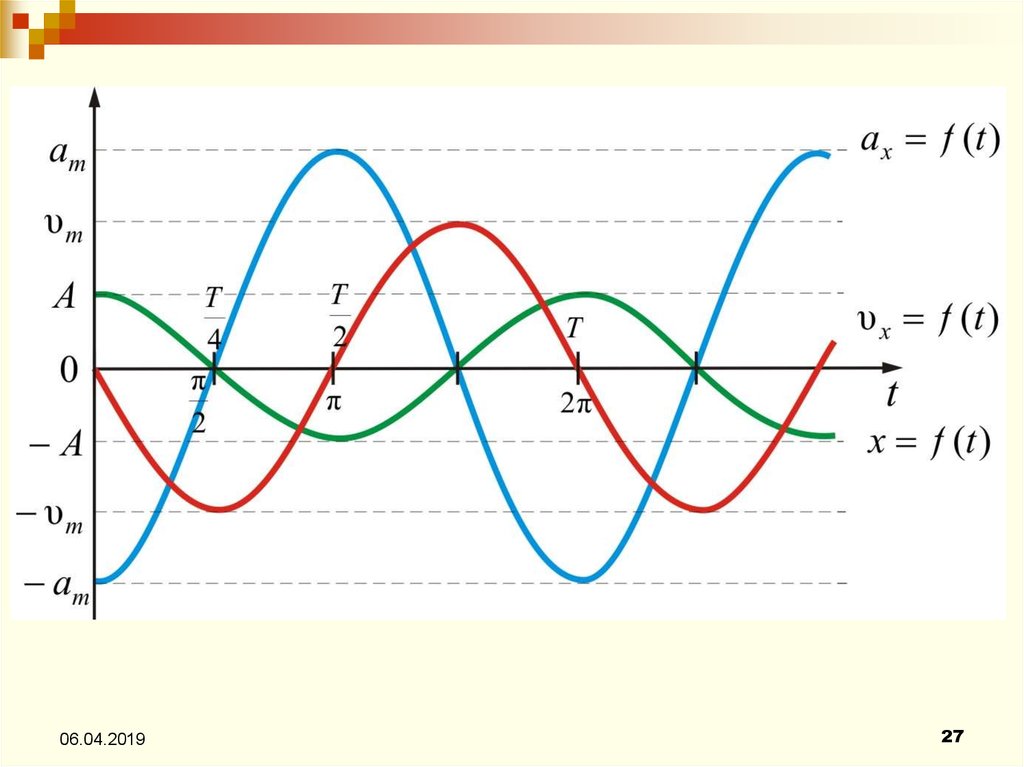
25.
Скорость колеблющейся точки меняется позакону:
dx
A sin( t 0 )
dt
A cos( t 0 )
2
26.
Ускорение:d
2
a
A cos( t 0 )
dt
A cos( t 0 )
2
27.
06.04.201927
28.
Динамика колебанийСила, действующая на точку массой m:
F ma m x
2
Сила, вызывающая колебания, обладает
следующими свойствами
1. направления силы и смещения
противоположны.
2. модуль силы пропорционален смещению
материальной точки из положения равновесия;
29.
Следовательно, сила всегда направлена кположению равновесия.
Такие силы называют возвращающими.
Зависимость F ma m 2 x характерна для
упругой силы. F = -kx
Силы другой физической природы,
удовлетворяющие тому же виду зависимости,
называют квазиупругими. Например, сила
тяжести.
30.
06.04.201930
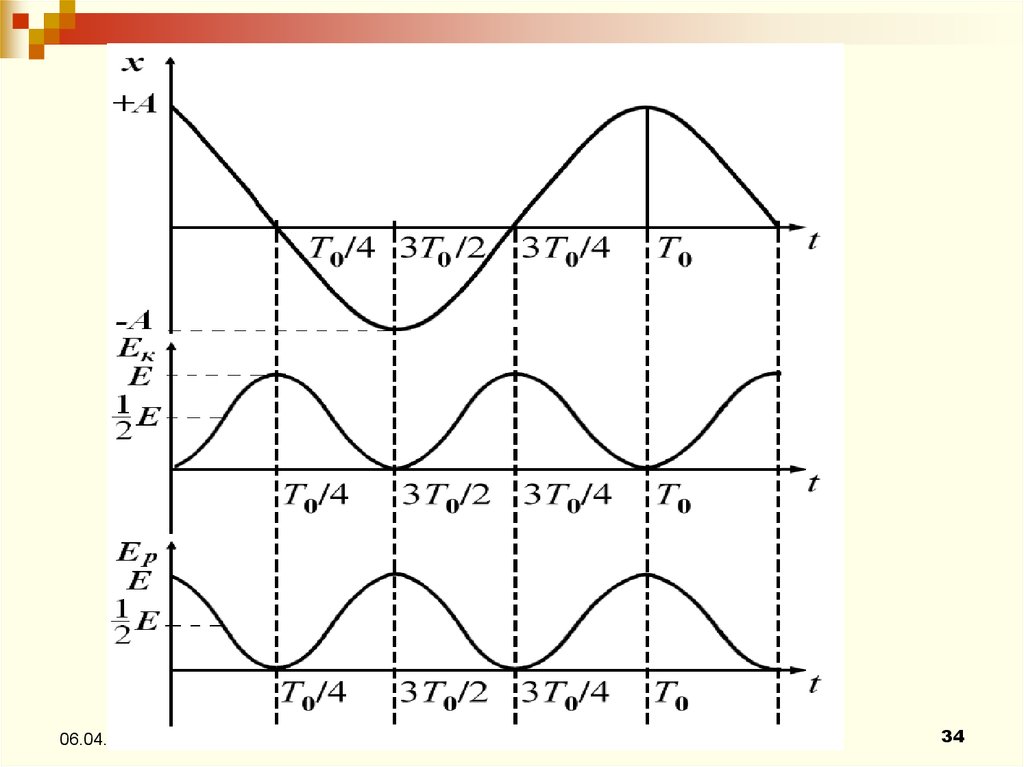
31.
ЭНЕРГИЯ ГАРМОНИЧЕСКИХКОЛЕБАНИЙ
Кинетическая энергия материальной
точки, совершающей гармонические
колебания:
m
m A
2
Ек
sin t 0
2 2 2 2
m A
1 cos2 t 0 .
2
4
2
2
32.
Потенциальная энергия материальнойточки, совершающей гармонические колебания
под действием упругой силы F:
m x
Е p Fdx
2
0
2
2
m A
2
cos t 0
2
x
2
2
m A
1 cos2 t 0 .
4
2
2
33.
Полная энергия:m A
E Ек Е p
2
2
k A
const ,
2
2
где
k m .
2
2
34.
06.04.201934
35.
Гармонический осцилляторОсциллятор – система, совершающая
свободные колебания.
Свободные
(собственные)
колебания
совершаются
за
счет
первоначально
сообщенной
энергии
при
последующем
отсутствии внешнего воздействия на
колебательную систему.
Классический осциллятор – механическая
система, совершающая колебания около
положения устойчивого равновесия (например,
пружинный маятник).
36.
Дифференциальное уравнение гармоническогоосциллятора
x x 0
2
Решение этого уравнения:
x A cos t 0
Здесь x – колеблющаяся величина.
37. Маятники Маятник- тело, совершающее колебания относительно положения равновесия под действием приложенных к нему сил. Пружинный
маятникфизический маятник
математический маятник
оборотный маятник
06.04.2019
37
38. Пружинный маятник это закреплённый на пружине груз, способный совершать колебания в вертикальном или горизонтальном или
направлении.Трением пренебрегаем. Груз имеет
массу m , жёсткость пружины равна k .
Координате x=0
отвечает
положение равновесия, в котором
пружина не деформирована..
06.04.2019
38
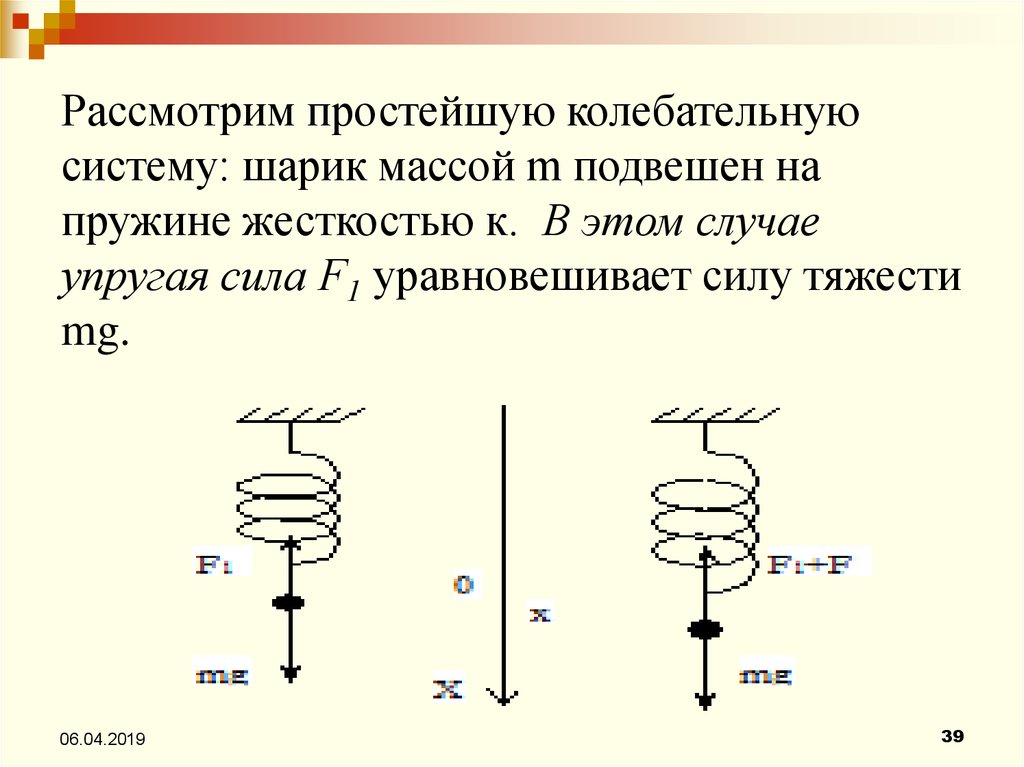
39.
Рассмотрим простейшую колебательнуюсистему: шарик массой m подвешен на
пружине жесткостью к. В этом случае
упругая сила F1 уравновешивает силу тяжести
mg.
06.04.2019
39
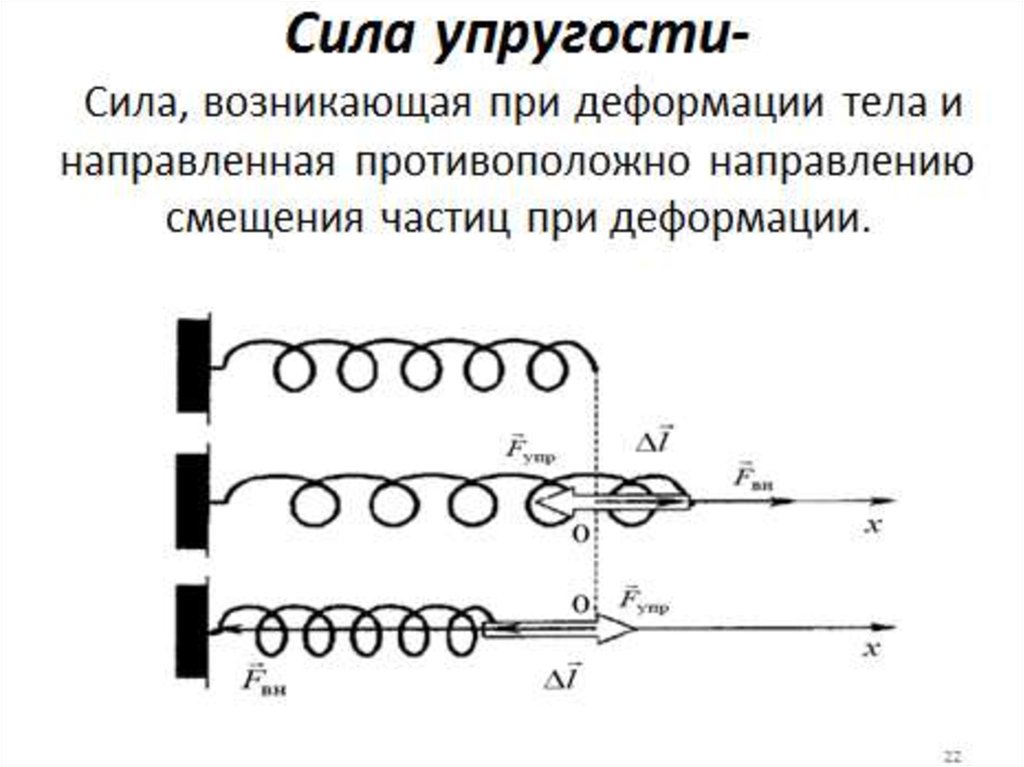
40.
Изменение упругой силы по закону Гукапропорционально изменению длины пружины
или смещению шарика х:
F=-kx,(1)
где k — жесткость пружины. Знак "-" отражает то
обстоятельство, что смещение и сила имеют
противоположные направления.
Сила F обладает следующими свойствами: 1) она
пропорциональна смещению шарика из
положения равновесия; 2) она всегда направлена
к положению равновесия.
В нашем примере сила по своей природе упругая
06.04.2019
40
41.
Уравнение второго закона Ньютонадля шарика имеет вид:
Введем обозначения
Тогда
Решение уравнения имеет вид
06.04.2019
41
42.
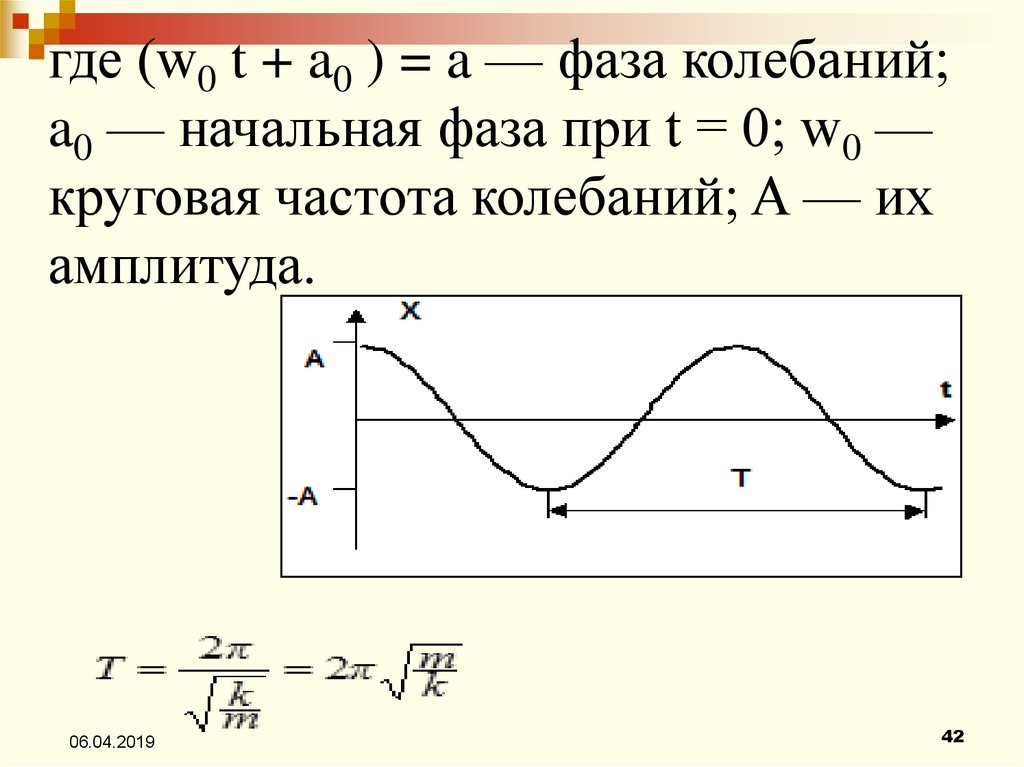
где (w0 t + a0 ) = a — фаза колебаний;a0 — начальная фаза при t = 0; w0 —
круговая частота колебаний; A — их
амплитуда.
06.04.2019
42
43.
Решив данное уравнение, получим, чтопружинный маятник совершает
гармонические колебания по закону
x = A cos(ω0t + φ0),
с циклической частотой
и периодом колебания
Эти формулы справедливы для упругих
колебаний в пределах, в которых выполняется закон Гука, т. е. когда масса пружины
мала по сравнению с массой тела
44.
В горизонтальном направлении на груз действуеттолько сила упругости со стороны пружины.
Второй закон Ньютона для груза в проекции на
ось имеет вид:
Если груз смещен вправо то сила упругости
направлена в противоположную сторону, и закон
Гука можно записать так:
06.04.2019
45.
Физический маятникТвердое тело, совершающее под действием силы
тяжести
колебания
вокруг
неподвижной
горизонтальной оси, проходящей через точку О, не
совпадающую с центром масс тела С. Точку О
называют точкой подвеса.
Если маятник отклонен из
положения равновесия на
некоторый угол a, то в
соответствии с уравнением
динамики вращательного движения твердого
46. тела момент M возвращающей силы можно записать в виде (1) где J — момент инерции маятника относительно оси, проходящей через
точку подвеса О, l –расстояние между ней и центром масс маятника
Ft = –mg sina (знак минус обусловлен тем, что
направления Ft и a всегда противоположны)
Уравнение (1) можно записать в виде
или
принимая
получим
46
47.
решение которого :При малых колебаниях физический маятник
совершает гармонические колебания с периодом
где L=J/(ml) — приведенная длина физического
маятника.
Точка О' на продолжении прямой ОС, отстоящая от
точки О подвеса маятника на расстоянии
приведенной длины L, называется центром
качаний физического маятника.
06.04.2019
47
48.
Приведенная длина физического маятника –это длина такого математического маятника,
период колебаний которого совпадает с
периодом колебаний данного физического
маятника.
J
L ,
ml
J – момент инерции маятника относительно оси,
проходящей через точку подвеса.
49.
Применяя теорему Штейнера, получимт. е. ОО' всегда больше ОС. Точка подвеса О
маятника и центр качаний О' обладают
свойством взаимозаменяемости: если точку
подвеса перенести в центр качаний, то прежняя
точка О подвеса станет новым центром качаний,
и период колебаний физического маятника не
изменится.
06.04.2019
49
50.
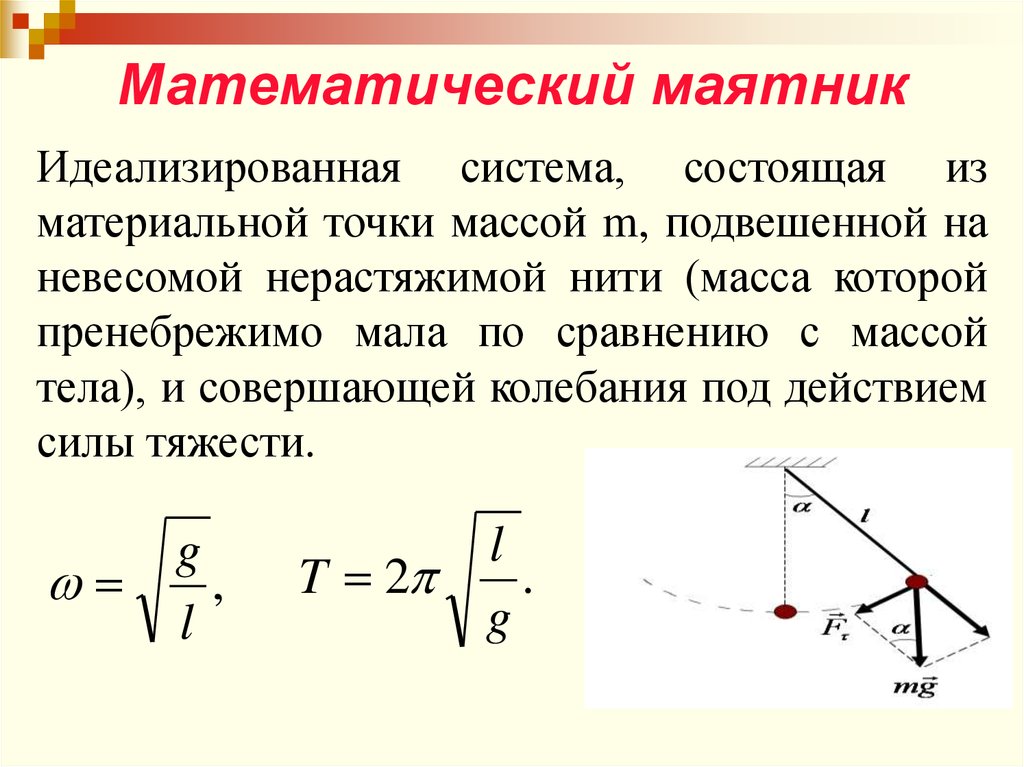
Математический маятникИдеализированная система, состоящая из
материальной точки массой m, подвешенной на
невесомой нерастяжимой нити (масса которой
пренебрежимо мала по сравнению с массой
тела), и совершающей колебания под действием
силы тяжести.
g
,
l
l
T 2
.
g
51.
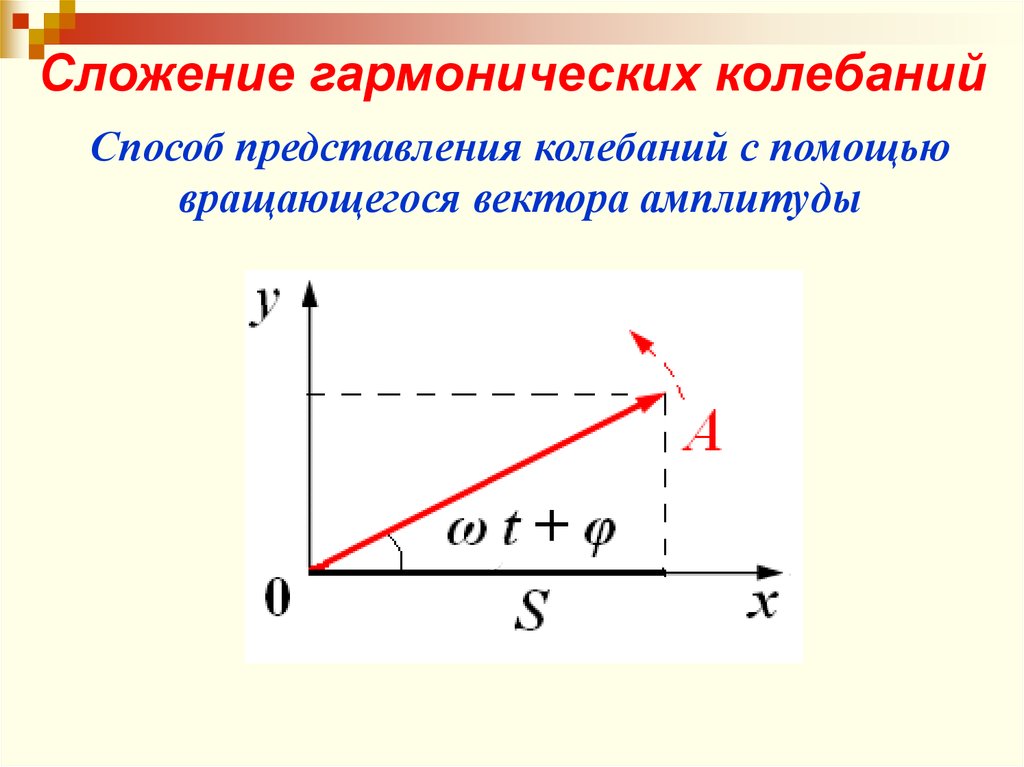
Сложение гармонических колебанийСпособ представления колебаний с помощью
вращающегося вектора амплитуды
52.
Сложение двух одинаковонаправленных колебаний
1. Сложение гармонических колебаний
одного направления и одинаковой
частоты
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
Разность фаз этих колебаний не зависит от
времени t, т.е. (φ1 – φ2) = const, такие колебания
называются когерентными
53.
AA
φ
2
φ
2
φ
A
φ
2
– φ
1
1
Для
нахождения
результирующего
колебания
воспользуемся методом
векторных диаграмм.
1
0
x
x Acos( t ), где
A A A 2 A1 A2 cos( 2 1 ),
2
2
1
2
2
A1sin 1 A2 sin 2
tg
.
A1cos 1 A2 cos 2
54.
Если колебания синфазны:φ2 – φ1 = ±2mπ,
следовательно, А = А1 + А2, происходит усиление
результирующего колебания.
Если колебания в противофазе: φ2 – φ1 = ±(2m +1)π,
следовательно, А = |А1 – А2|, происходит ослабление
результирующего колебания.
Некогерентные колебания: ω1 ≠ ω2, т.е. разность
фаз колебаний
(ω1 + φ1 – ω2 – φ2) ≠ const и изменяется с течением
времени t.
При наложении таких колебаний получаются
негармоническое результирующее колебание.
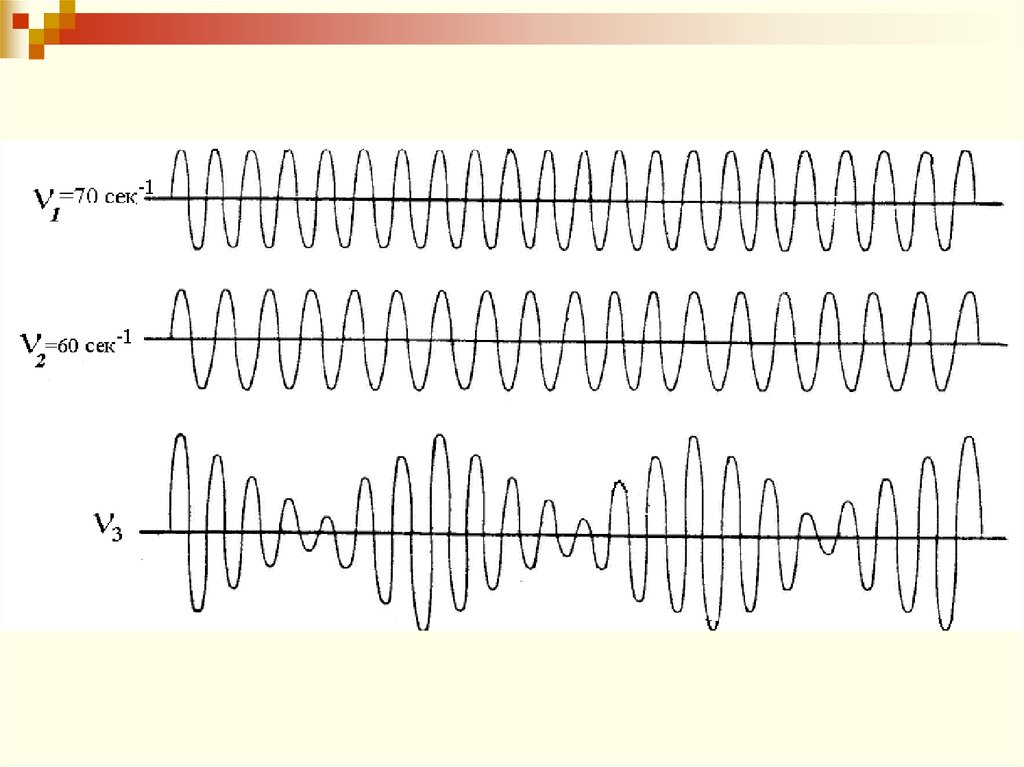
55.
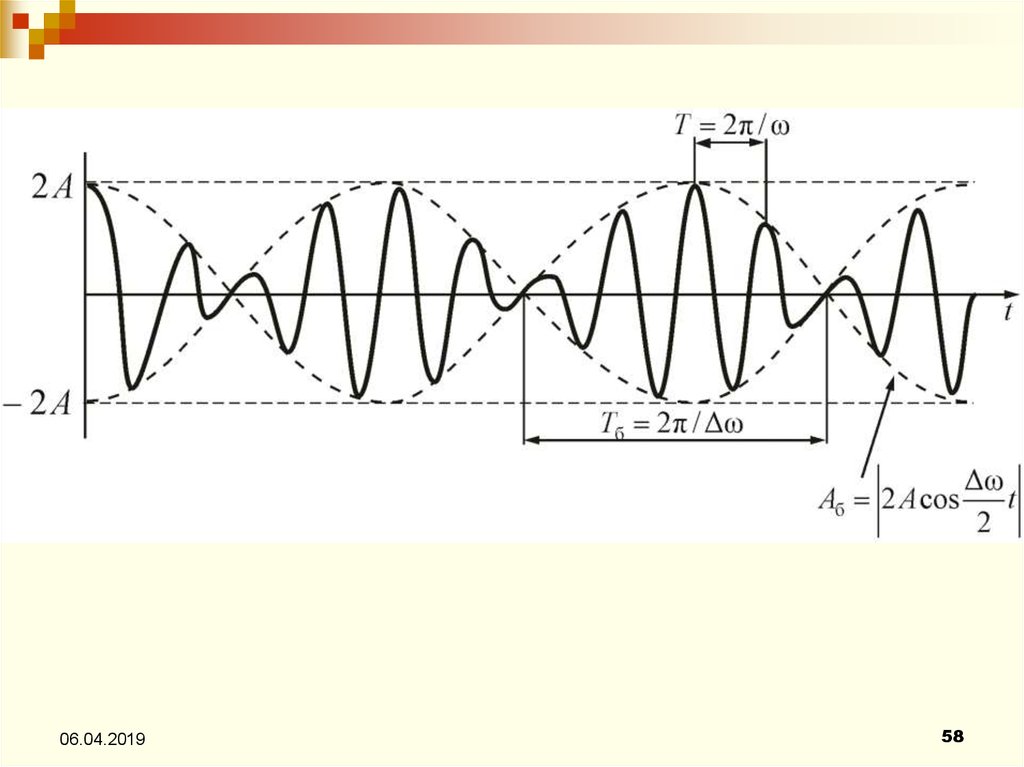
Сложение гармонических колебанийодного направления с частотами
неравными, но близкими - биения
2.
Если амплитуды двух гармонических колебаний,
направленных вдоль одной прямой, одинаковы
А1 = А2 = А, а их частоты мало отличаются друг от
друга Δω = ω2 – ω1 << ω1, то результирующее сложение
этих колебаний получается с периодически
изменяющейся амплитудой Аб.
Уравнения колебаний
имеют вид :
x1 Acos t ,
x2 Acos( )t.
56.
Периодические изменения амплитуды от минимальногозначения до максимального называются биениями.
Уравнение результирующего колебания
x x1 x 2 A cos t cos( )t
2
2Acos
t
t cos
t
2
2
2
2 Аcos
t cos t.
2
Аб
06.04.2019
56
57.
Результирующее колебание можно рассматривать какгармоническое с частотой , амплитуда Аб которого
изменяется по периодическому закону:
Аб 2 А cos
t.
2
Частота изменения Аб в два раза больше частоты
изменения косинуса (т.к. берется по модулю), т.е.
частота биений равна разности частот складываемых
колебаний:
.
б
Период биений
06.04.2019
2
Тб
.
57
58.
06.04.201958
59.
60.
Гармоническиеколебания
совпадают
по
направлению и имеют кратные циклические частоты
ω, 2ω, 3ω и т.д. В результате их сложения получаются
периодические негармонические колебания с периодом
Т = 2π ∕ ω.
В свою очередь, любое сложное периодическое
колебание S = f(t) можно представить в виде суммы
простых гармонических колебаний с циклическими
частотами, кратными основной циклической частоте ω0
= 2π ∕ Т, где Т – период колебаний:
A0
S f t
A1cos 0 t 1 A2 cos 2 0 t 2 ... An cos n 0t n
2
A0
An cos n 0 t n ,
2 n 1
60
61.
Такое представление периодической функции f(t) называетсяразложением функции в ряд Фурье или гармоническим
анализом сложного периодического колебания.
Члены ряда Фурье, соответствующие гармоническим
колебаниям с циклическими частотами ω0, 2ω0, 3ω0 …
называются первой (основной), второй, третьей и т.д.
гармониками сложного периодического колебания S = f(t).
Совокупность этих гармоник образуют спектр колебаний
S = f(t).
В простейших случаях спектр может состоять из
небольшого числа гармоник.
Часто под спектром колебаний понимают спектр
(совокупность) его частот.
06.04.2019
61
62.
3. Сложение взаимноперпендикулярных колебаний
Сложение колебаний с одинаковыми
частотами ( 1 : 2=1:1 )
Пусть точка одновременно движется вдоль осей x и y:
x A1cos( t 1 ),
y A2 cos( t 2 ).
x 2 y 2 2 xy
2
2
cos 2 1 sin 2 1 .
2
A1 A2 A1 A2
63.
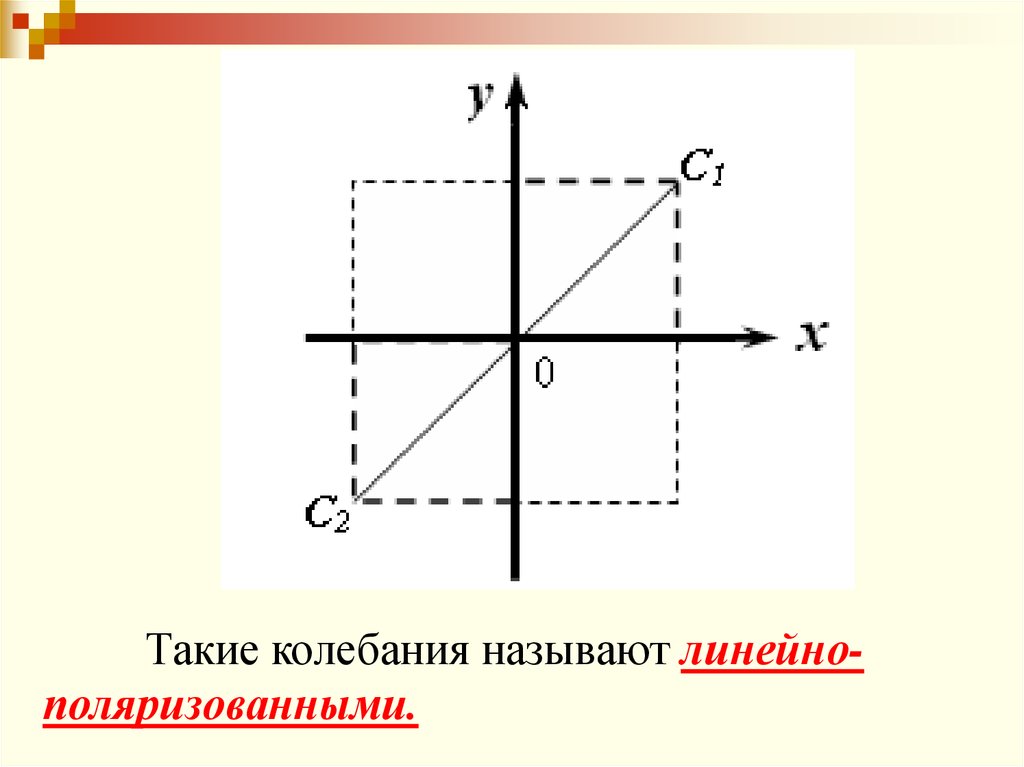
Рассмотрим несколько частных случаев:1) Фазы колебаний равны.
x = A1 sin t;
y = A2 sin t.
x A1
y A2
или
A2
y
x
A1
64.
Такие колебания называют линейнополяризованными.65.
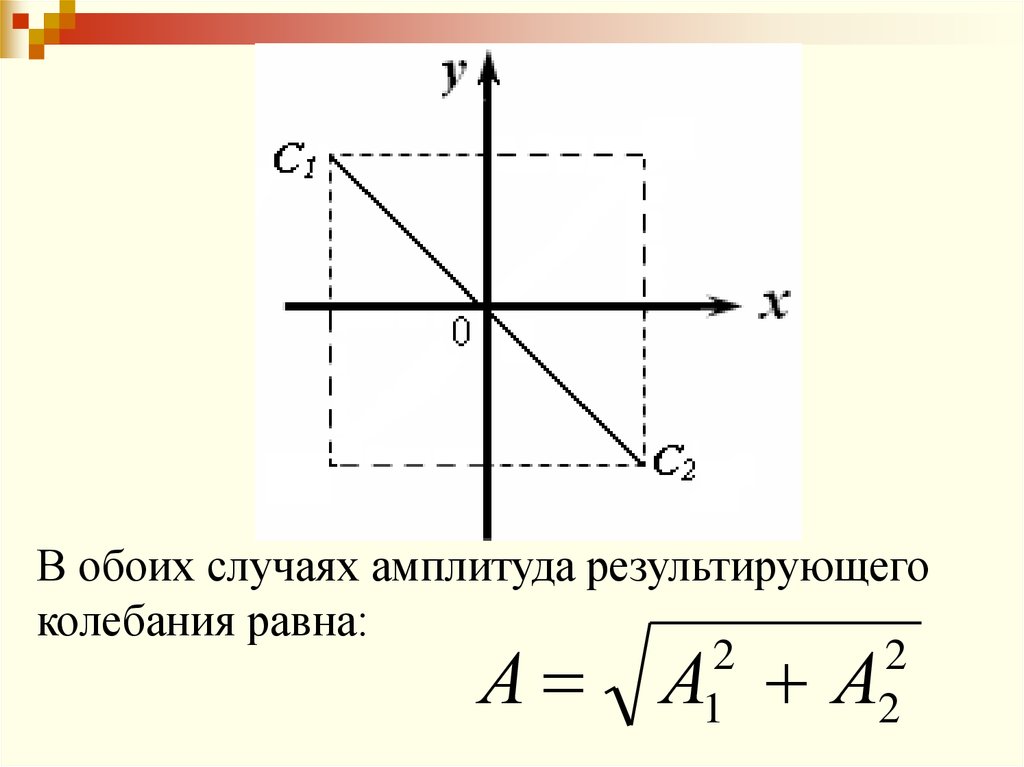
2) Разность фаз равна π.x = A1 sin ( t + ) = - A1 sin t;
y = A2 sin t.
x
A1
y
A2
или
A2
y
x
A1
66.
В обоих случаях амплитуда результирующегоколебания равна:
2
2
1
2
А А А
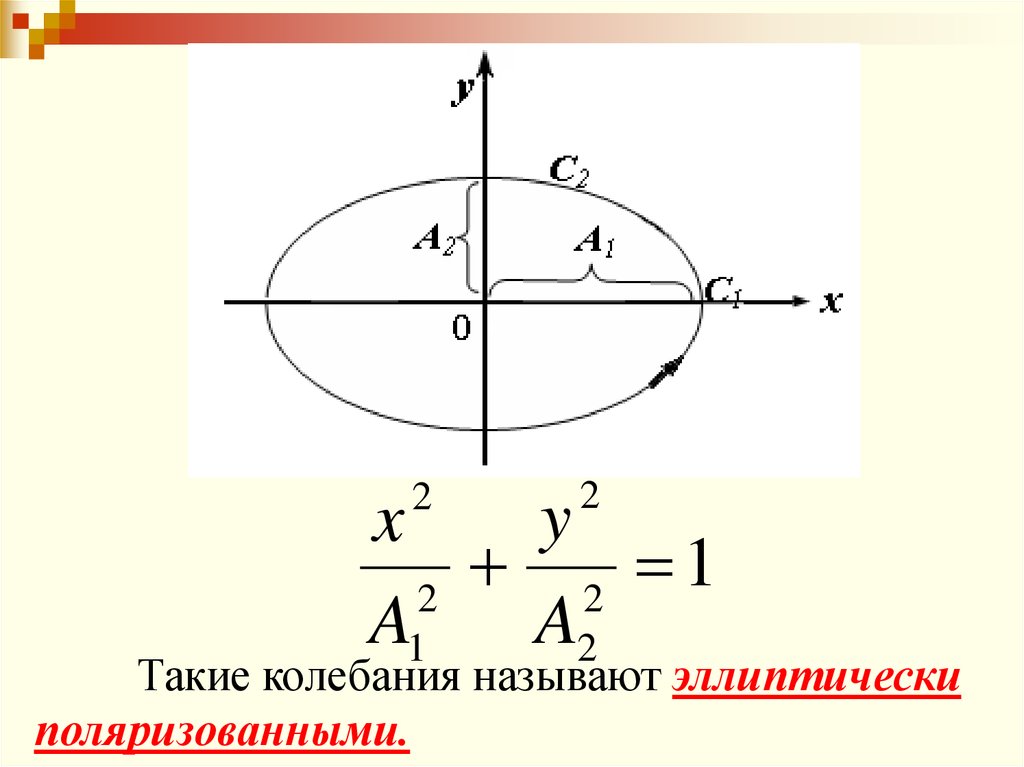
67.
3) Разность фаз равна π/2.x A1 sin t A1 cos t ;
2
y A2 sin t.
x
cos t;
A1
y
sin t.
A2
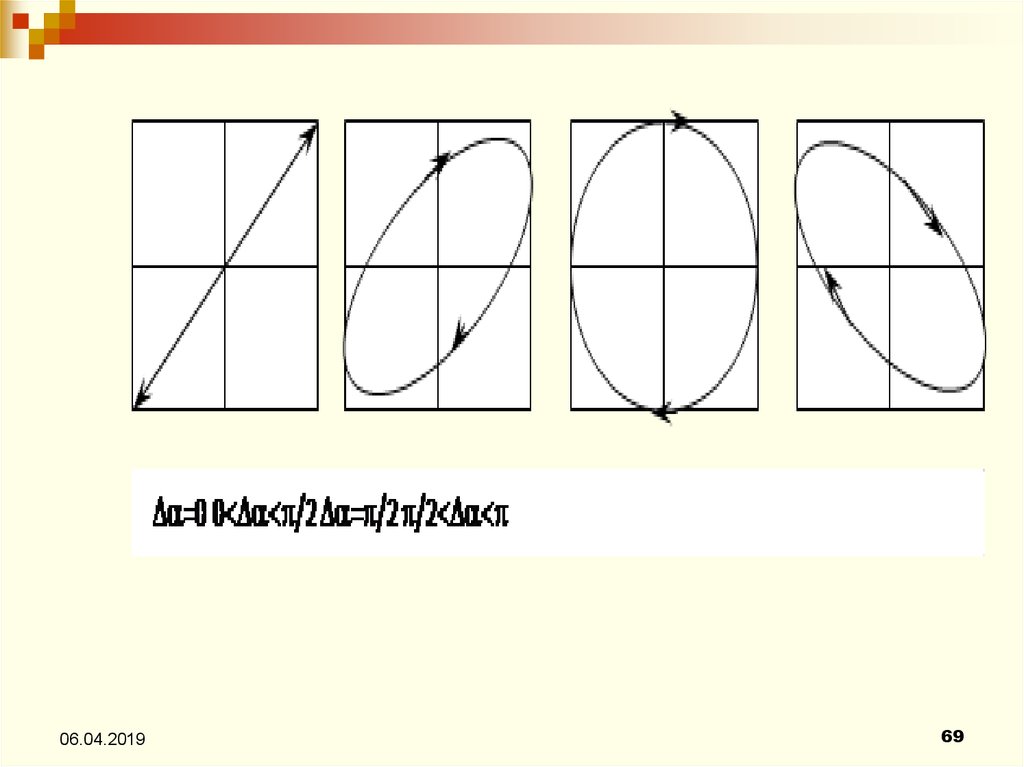
68.
22
y
x
1
2
2
A1
A2
Такие колебания называют эллиптически
поляризованными.
69.
06.04.201969
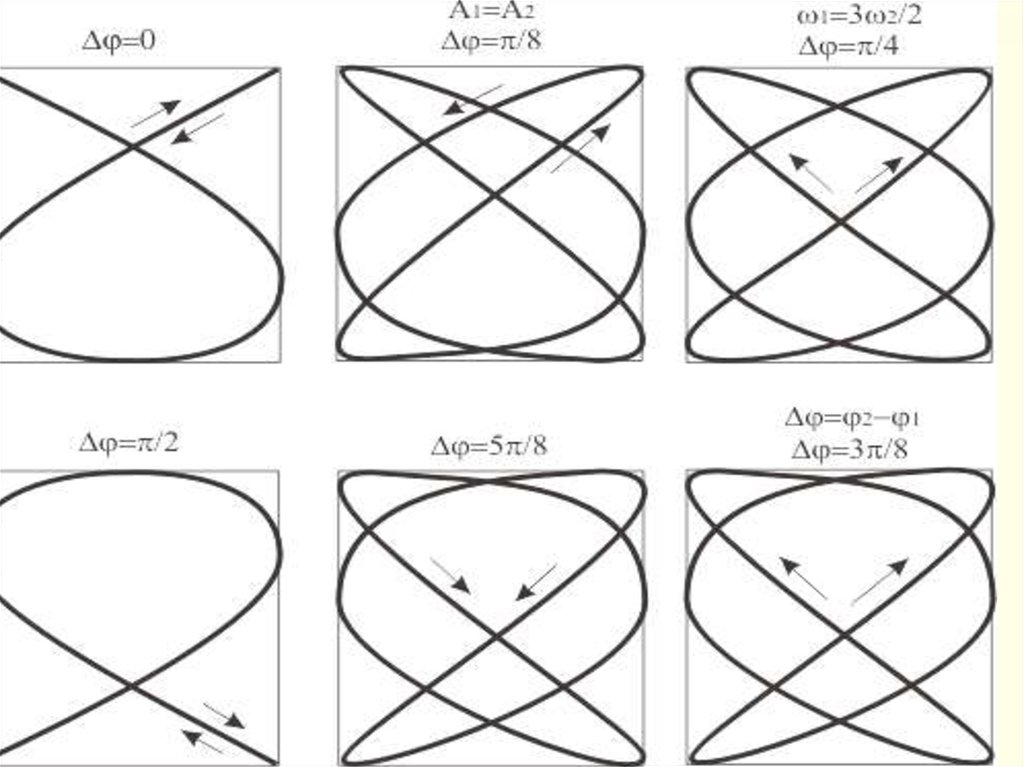
70.
Сложение колебаний с разнымичастотами
Если частоты складываемых колебаний относятся
друг к другу как целые числа, то траектория
результирующего движения оказывается замкнутой, а
само движение – периодическим.
Прочерчиваемые точкой замкнутые траектории,
образующиеся при целочисленных отношениях частот
складываемых взаимно-перпендикулярных колебаний
называют фигурами Лиссажу.
Вид фигур Лиссажу зависит от соотношения амплитуд,
частот и начальных фаз складываемых колебаний.
71.
06.04.201971
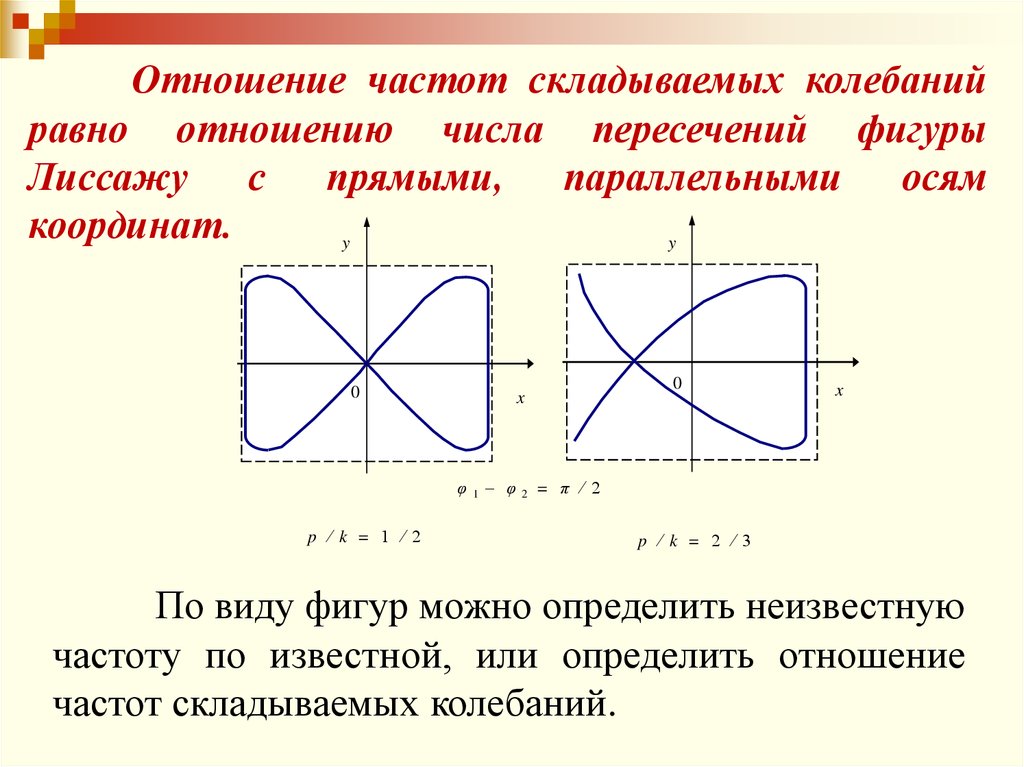
72.
Отношение частот складываемых колебанийравно отношению числа пересечений фигуры
Лиссажу
с
прямыми,
параллельными
осям
координат.
y
y
0
φ
p ∕ k = 1 ∕ 2
0
x
1
– φ
2
x
= π ∕ 2
p ∕ k = 2 ∕ 3
По виду фигур можно определить неизвестную
частоту по известной, или определить отношение
частот складываемых колебаний.
73.
Фигуры Лиссажу при06.04.2019
ω1 ω 2
73
74.
Затухающие колебанияЗатухающие колебания – колебания,
амплитуда которых из-за потерь энергии
реальной колебательной системой с течением
времени уменьшается.
Свободные колебания реальной системы
всегда затухают. Причиной затухания
механических колебаний является трение,
электрических колебаний – тепловые потери в
проводниках.
75.
Закон затухания колебанийопределяется свойствами колебательных
систем.
Обычно рассматриваются линейные
системы – идеализированные реальные
системы, в которых параметры,
определяющие физические свойства
системы, в ходе процесса не изменяются.
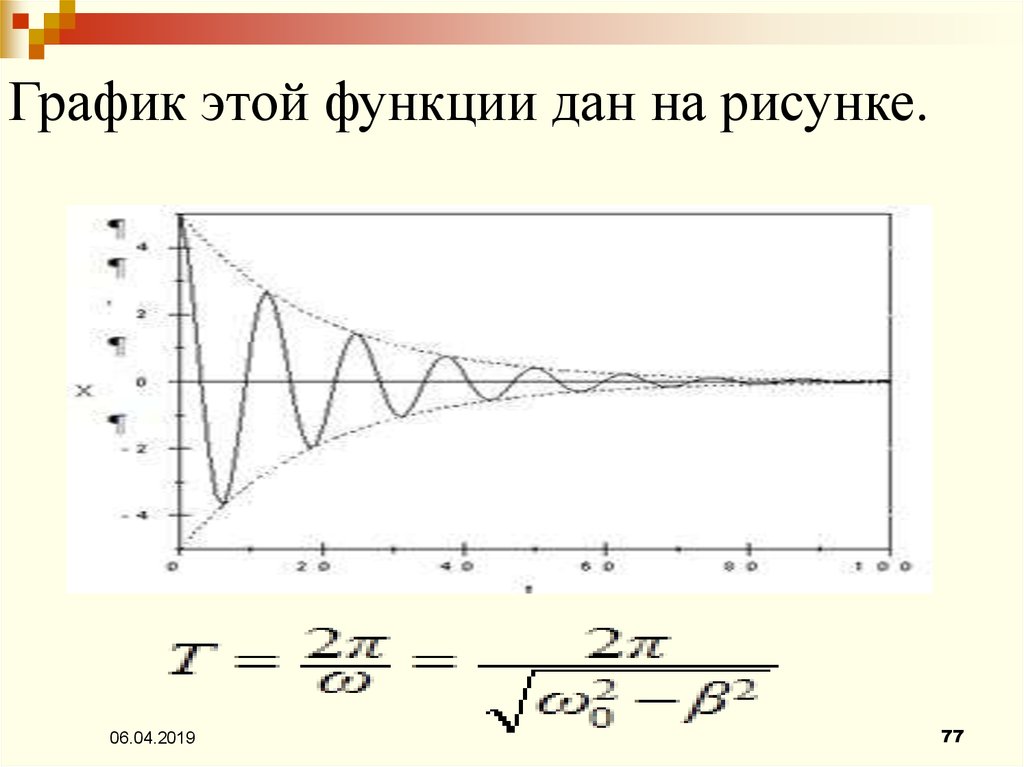
76.
Дифференциальное уравнение свободных затухающихколебаний линейной системы:
х – колеблющаяся величина,
β = const – коэффициент затухания,
ω0 – собственная циклическая частота колебательной
системы (т.е. в отсутствие потерь энергии, β = 0).
Решение уравнения в виде
06.04.2019
76
77.
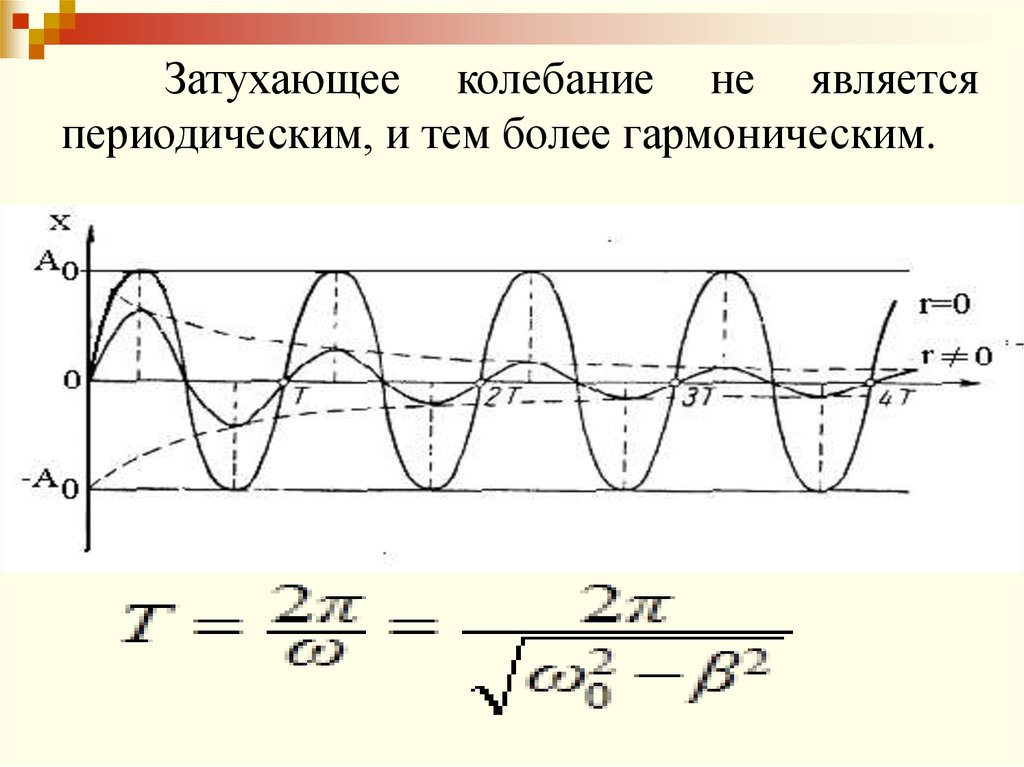
График этой функции дан на рисунке.06.04.2019
77
78.
Для пружинного маятника массой m,совершающего малые колебания под действием
упругой силы, сила трения пропорциональна
скорости:
Fтр r rx ,
r- коэффициент сопротивления.
Дифференциальное уравнение затухающих
колебаний маятника:
2
d x
dx
m 2 r
kx 0
dt
dt
79.
Амплитуда затухающих колебаний:Это отношение называют декрементом затухания .
В качестве меры затухания часто берут величину
натурального логарифма
80.
Затухающее колебание не являетсяпериодическим, и тем более гармоническим.
81.
Вынужденные колебанияВынужденные
колебания
–
незатухающие колебания, возникающие под
действием периодической силы, изменяющейся
по гармоническому закону:
X t X 0 cos t
Для механических колебаний роль X(t) играет
внешняя вынуждающая сила
F F0 cos t
82.
Для простейшего пружинного маятника, накоторый
действует
внешняя
сила
Дифференциальное уравнение вынужденных
колебаний маятника:
:
83.
В установившемся режиме вынужденныеколебания являются гармоническими,
происходят с частотой внешней гармонической
силы.
84.
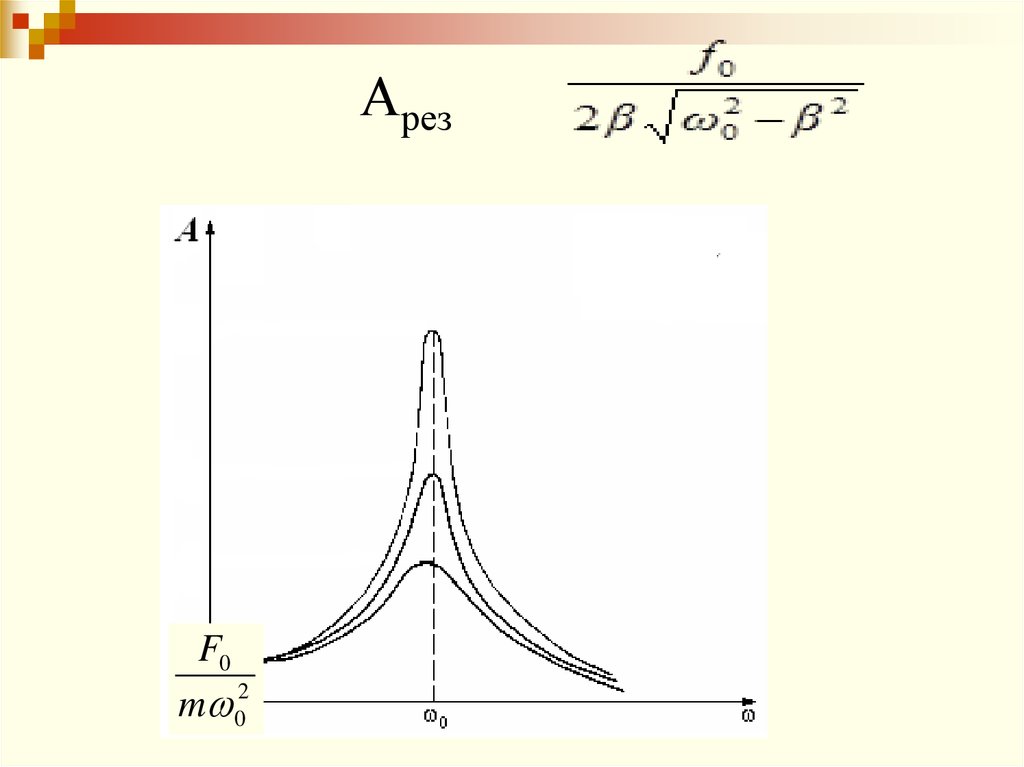
В случае установившихся колебаний принекоторой частоте внешней силы – резонансной
частоте ωрез – амплитуда смещения достигает
максимального значения:
Явление резкого возрастания амплитуды
вынужденных колебаний при приближении
частоты вынуждающей силы к частоте, равной
или близкой собственной частоте колебательной
системы,
называется
механическим
резонансом.
85.
АрезF0
m 02































































 Физика
Физика








