Электротехника и электроника. Цепи с распределенными параметрами. (Лекция 15)

1.

Кубанский государственный технологический университет
Институт информационных технологий и безопасности
Кафедра компьютерных технологий и информационной
безопасности
Учебная дисциплина
Электротехника и электроника
Лекция № 15
Цепи с распределенными
параметрами

2. 4. Использование отрезков длинной линии в качестве элементов селективных цепей СВЧ техники.

Учебные вопросы:
1. Основные понятия цепей с распределенными
параметрами.
2. Телеграфные уравнения и их общее решение для режима
гармонических колебаний.
3. Режимы работы длинных линий.
4. Использование отрезков длинной линии в качестве
элементов селективных цепей СВЧ техники.
Литература:
Литература
1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории
цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 344 –350.
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 235 –
245.
3. Фрикс В.В. Основы теории цепей: Учебное пособие для межвузовского
использования вузов, - М.: Радио Софт, 2002 г, с. 219 –228.

3.

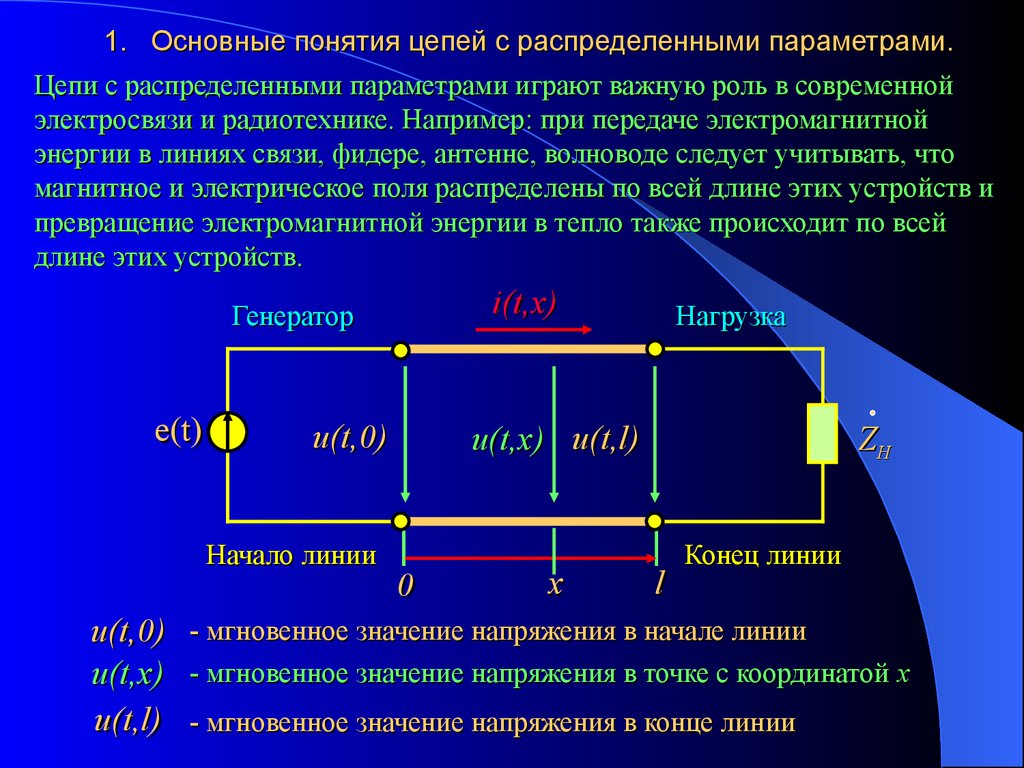
1. Основные понятия цепей с распределенными параметрами.
Цепи с распределенными параметрами играют важную роль в современной
электросвязи и радиотехнике. Например: при передаче электромагнитной
энергии в линиях связи, фидере, антенне, волноводе следует учитывать, что
магнитное и электрическое поля распределены по всей длине этих устройств и
превращение электромагнитной энергии в тепло также происходит по всей
длине этих устройств.
i(t,x)
Генератор
e(t)
u(t,0)
Начало линии
u(t,0)
u(t,x)
u(t,l)
Нагрузка
u(t,x) u(t,l)
0
x
ZH
l
Конец линии
- мгновенное значение напряжения в начале линии
- мгновенное значение напряжения в точке с координатой х
- мгновенное значение напряжения в конце линии

4.

Под генератором e(t) будем понимать источник сигналов, микрофон, усилитель,
выходной каскад передатчика.
В качестве комплексной нагрузки ZH может быть телефон, антенна.
Ток и напряжение на выходе в конце сколь угодно малого участка (отрезка)
цепи с распределенными параметрами не равны соответственно току и
напряжению на его входе и отличаются как по величине, так и по фазе.
Ток и напряжение в любой точке цепи являются не только функциями
времени t, но и пространственных координат (например – х –расстояние от
одного из концов линии.
Цепи с распределенными параметрами характеризуются проходящими в них
волновыми процессами. Поэтому напряжения и токи изменяются не только
во времени, но и в пространстве: u(t,x); i(t,x)
u (t , x) u (t T , x)
T период
u (t0 , x) u (t0 , x )
В любой точке c
координатой х
В любой фиксированный
момент времени t0
длина волны
Длинными линиями называются линии, геометрическая длина
которых больше длины волны в 10 раз: l > 10 .
l

5.

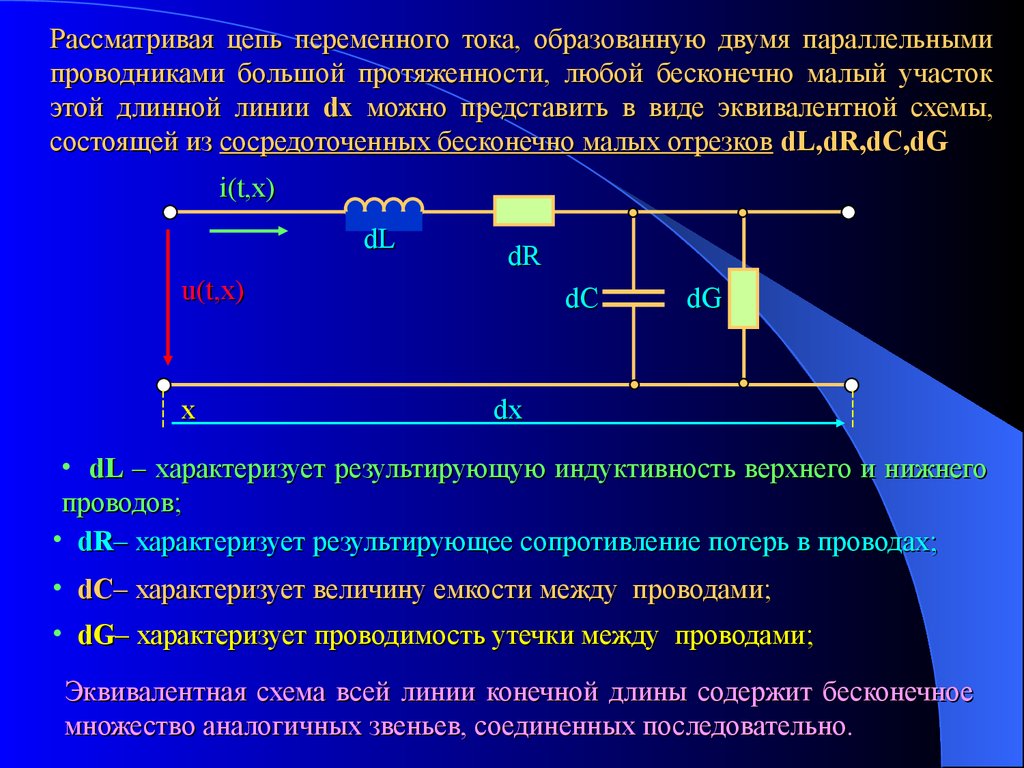
Рассматривая цепь переменного тока, образованную двумя параллельными
проводниками большой протяженности, любой бесконечно малый участок
этой длинной линии dx можно представить в виде эквивалентной схемы,
состоящей из сосредоточенных бесконечно малых отрезков dL,dR,dC,dG
i(t,x)
dL
dR
u(t,x)
x
dC
dG
dx
• dL – характеризует результирующую индуктивность верхнего и нижнего
проводов;
• dR– характеризует результирующее сопротивление потерь в проводах;
• dС– характеризует величину емкости между проводами;
• dG– характеризует проводимость утечки между проводами;
Эквивалентная схема всей линии конечной длины содержит бесконечное
множество аналогичных звеньев, соединенных последовательно.

6.

Первичные параметры длинной линии
В практических целях вместо бесконечно малых величин dL,dR,dC,dG
удобнее использовать так называемые первичные параметры ( погонные)
параметры линии, рассчитанные на единицу длины.
dR
R0
dx
погонное сопротивление, Ом/м
dL
L0
dx
погонная индуктивность, Гн/м
dC
C0
dx
погонная емкость, Ф/м
dG
G0
dx
погонная проводимость, См/м
Однородной длинной линией называется такая линия, первичные
параметры которой неизменны (постоянны) по всей ее длине.

7.

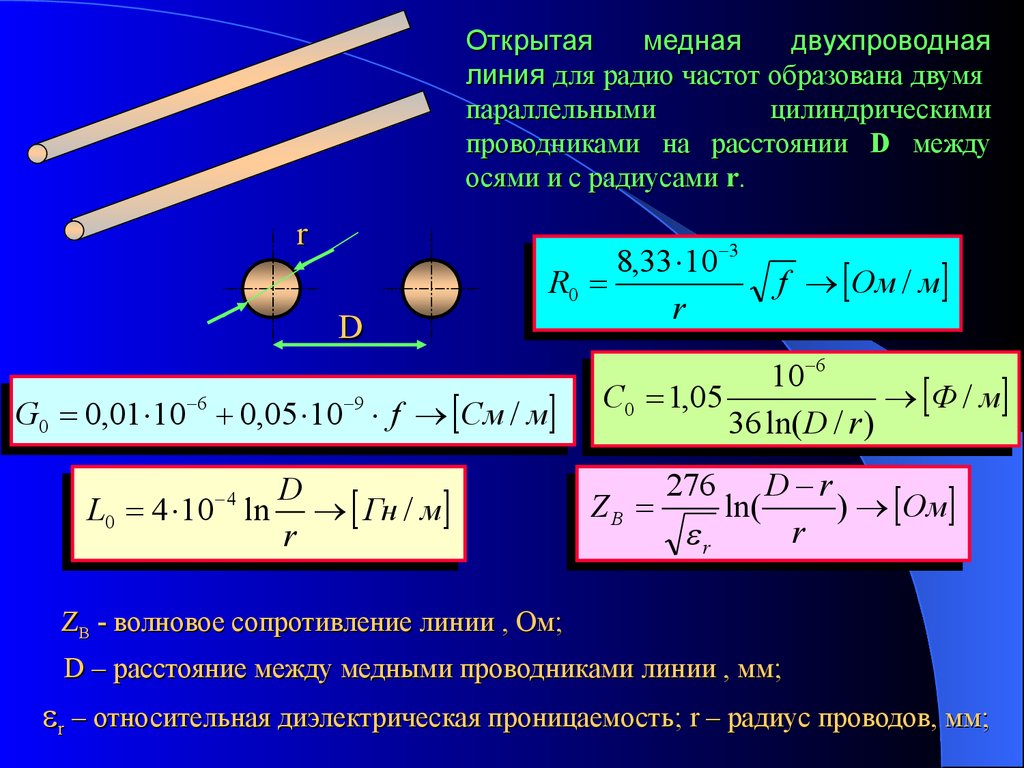
Открытая
медная
двухпроводная
линия для радио частот образована двумя
параллельными
цилиндрическими
проводниками на расстоянии D между
осями и с радиусами r.
r
D
8,33 10 3
R0
r
G0 0,01 10 6 0,05 10 9 f См / м
D
L0 4 10 ln Гн / м
r
4
f Ом / м
10 6
С0 1,05
Ф / м
36 ln( D / r )
ZB
276 D r
ln(
) Ом
r
r
ZB - волновое сопротивление линии , Ом;
D – расстояние между медными проводниками линии , мм;
r – относительная диэлектрическая проницаемость; r – радиус проводов, мм;

8.

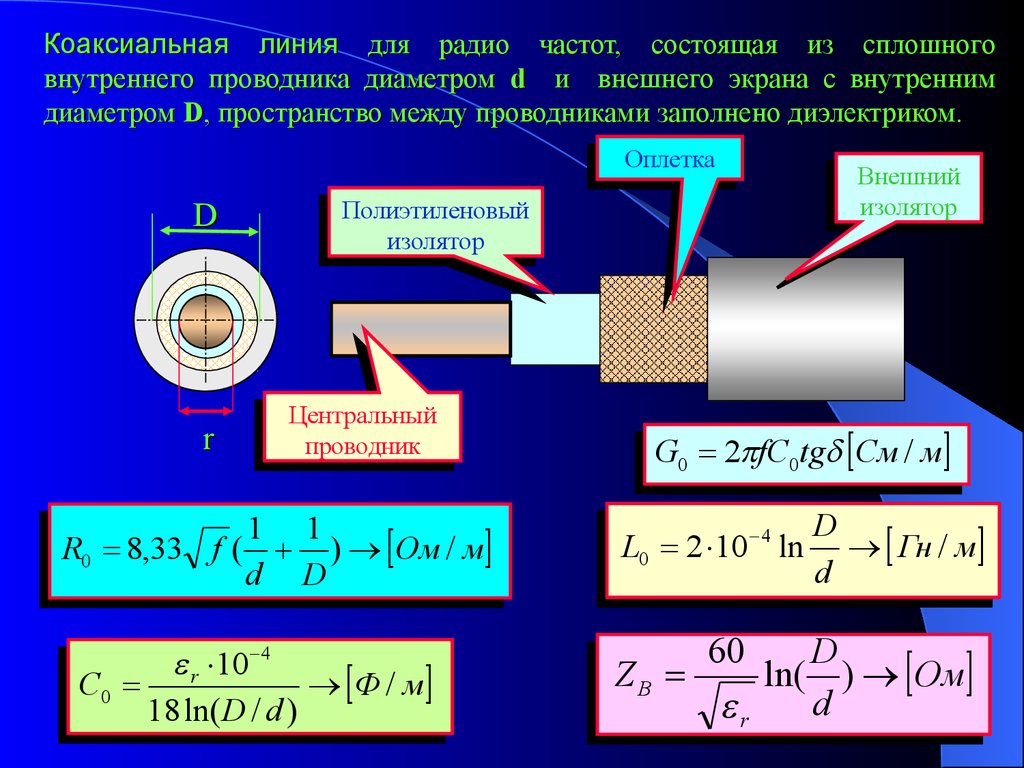
Коаксиальная линия для радио частот, состоящая из сплошного
внутреннего проводника диаметром d и внешнего экрана с внутренним
диаметром D, пространство между проводниками заполнено диэлектриком.
Оплетка
Оплетка
D
r
Полиэтиленовый
Полиэтиленовый
изолятор
изолятор
Центральный
Центральный
проводник
проводник
1 1
R0 8,33 f ( ) Ом / м
d D
r 10 4
С0
Ф / м
18 ln( D / d )
Внешний
Внешний
изолятор
изолятор
G0 2 fC0tg Cм / м
L0 2 10 4 ln
D
Гн / м
d
60
D
ZB
ln( ) Ом
d
r

9.

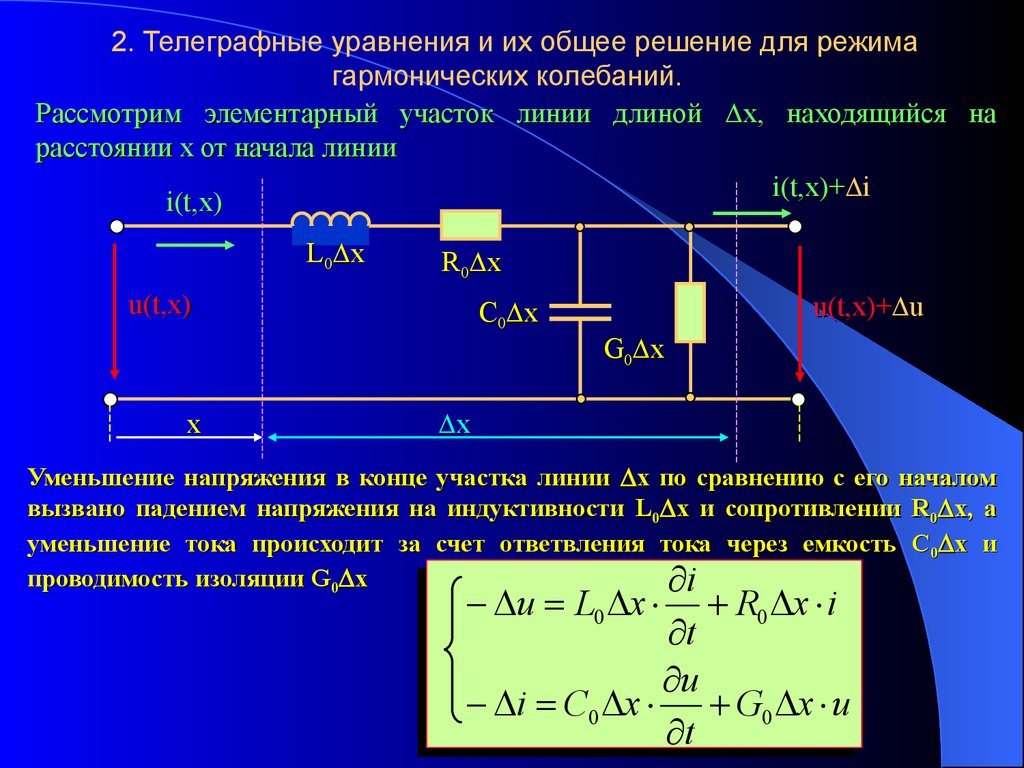
2. Телеграфные уравнения и их общее решение для режима
гармонических колебаний.
Рассмотрим элементарный участок линии длиной х, находящийся на
расстоянии х от начала линии
i(t,x)+ i
i(t,x)
L0 x
R0 x
u(t,x)
x
C0 x
u(t,x)+ u
G0 x
x
Уменьшение напряжения в конце участка линии x по сравнению с его началом
вызвано падением напряжения на индуктивности L0 х и сопротивлении R0 х, а
уменьшение тока происходит за счет ответвления тока через емкость С 0 х и
проводимость изоляции G0 х
i
u L0 x
R0 x i
t
u
i C0 x G0 x u
t

10.

Разделив обе части этих уравнений на х и перейдя к пределу при х 0,
получим дифференциальные уравнения линии
u
i
L0 R0 i
t
t
i
u
C0
G0 u
t
t
Телеграфные
уравнения
Найдем законы изменения амплитуд и фаз напряжений и токов в линии для
режима установившихся гармонических колебаний (считая известным закон
изменения токов и напряжений в линии)
Используя символический метод анализа гармонических колебаний:
u U
i I
dU
( R0 j L0 ) I
dx
dI
(G0 j C0 ) U
dx
du
j U
dt
di
j I
dt
Так как комплексные значения U и I
являются функциями только х, то
уравнения записываются не в частных,
а в полных производных

11.

Продифференцировав первое уравнение системы по х и подставив в него
второе, получим
2
d U
( R0 j L0 ) (G0 j C0 ) U
2
dx
Введя в рассмотрение
обозначение
( R0 j L0 ) (G0 j C0 )
Коэффициент распространения в линии
22
dd U
U 22 U 0
U 0
22
dx
dx
Уравнение Гельмгольца
(волновое уравнение)
Z 0 Y 0 ( R0 j L0 )(G0 j C0 ) j e j ;
2 2
-коэффициент ослабления, т.е. величина потерь в линии: = cos( )
-коэффициент фазы, т.е. величина фазового сдвига в линии:
линии = sin( )

12.

Решение телеграфных уравнений
22
Корни характеристического уравнения
dd U
U 22 U 0
22 U 0
dx
dx
p 2 2 0 p1, 2
Общее решение этого дифференциального уравнения для напряжения в точке
х запишется в виде:
x
x
U ( x ) A e
B e
Из первого уравнения системы выразим ток
1
dU
x
x
I
( A e B e )
R0 j L0 dx
R0 j L0
R0 j L0
ZB
G0 j C0
Общее решение для тока
Волновое
сопротивление линии
R0 L0
G0 C0
Условие
Хевисайда
1
xx
xx
1
A ee B
B ee ))
II((хх)) ((A
ZZBB

13.

U ( x) A e
x
B e
С учетом начальных условий при
х = 0:
x
1
I ( х)
Искомая система уравнений преобразуется к виду:
U 1 A B
Решение
I 1 Z B A B
U 1 I 1 Z B x U 1 I 1 Z B x
Ux
e
e
2
2
Ix
I x I ( x 0) I1
ZB
U x U ( x 0) U1
( A e x B e x )
U 1 I 1 Z B
A
2
U 1 I 1 Z B
B
2
U 1 I 1 Z B
2 ZB
e
x
U 1 I 1 Z B
2 ZB
e
x
Уравнения передачи
однородной длинной
линии

14.

Падающие и отраженные волны в длинных линиях.
U 1 I 1 Z B x U 1 I 1 Z B x
Ux
e
e
2
2
Ix
U 1 I 1 Z B
e
x
2 ZB
U 1 I 1 Z B
e
x
2 ZB
U 1 I 1 Z B
A
U П ( х)
2
U 1 I 1 Z B
B
U О ( х)
2
С учетом таких обозначений запись уравнений передачи линии упростится
xx
U
Uxx U
UПП((хх)) ee
xx
U
UОО((хх)) ee U
UПАД
U
UОТР
ПАД((хх))
ОТР((хх))
U
(
х
)
U
(
х
)
П
О
U
U
П ( х ) xx
О ( х ) xx
IIxx ee ee IIПАД
((хх)) IIОТР
((хх))
ПАД
ОТР
ZZBB
ZZBB
Напряжение и ток состоят из сумм двух слагаемых. Первые уменьшаются с
увеличением расстояния от начала линии х, а вторые возрастают. В линии
существуют два типа волн: падающие и отраженные волны.

15.

Уравнения передачи для мгновенных значений напряжений и токов
U x (t ) U П e
t
t
sin( t x) U O e sin( t x)
U О t
U П t
I x (t )
e sin( t x B )
e sin( t x B )
ZB
ZB
Ux ПАД
1
2
x1
x2
3
- t
·e- t
UUПП·e
Направление распространения
падающей волны
x3
Скорость распространения вдоль
линии состояния равной фазы
называется фазовой скоростью
x
х2 х1
Ф
t 2 t1

16.

U x (t ) U П e t sin( t x) U O e t sin( t x)
U П t
U О t
I x (t )
e sin( t x B )
e sin( t x B )
ZB
ZB
Эти слагаемые описывают волны точно такого же характера, как и падающие,
но распространяющиеся в обратном направлении, т.е. от конца линии к началу.
Такие волны называются отраженными волнами напряжения и тока.
Амплитуды отраженных волн убывают от конца линии к началу. Наибольшая
амплитуда отраженных волн наблюдается в конце линии.
U ( х) U ПАД ( х) U ОТР ( х)
x=l
I ( х) I ПАД ( х) I ОТР ( х)
I (l ) I 2 I 2 ПАД I 2ОТР
U
U 22 II22 ZZHH U
U 22ПАД
U
U 22ОТР
ПАД
ОТР
U (l ) U 2 U 2 ПАД U 2ОТР
II22 ZZ ВВ U
U 22ПАД
U
U 22ОТР
ПАД
ОТР

17.

ZHH ZZBB
Z
U22ПАД
II22
ПАД
U
22
Решения этой
системы уравнений
ZHH ZZBB
Z
U22ОТР
II22
ОТР
U
22
Отношение комплексной амплитуды отраженной волны к
комплексной
амплитуде
падающей
волны
называется
коэффициентом отражения по напряжению
U
Z
Z
H
B
22ОТР
U
Z
Z
UU ОТР H B ;;
U
UU U
22ОТР
22ПАД
U
U
ОТР
ПАД
U
ZZHH ZZBB
U22ПАД
ПАД
Коэффициент отражения по напряжению показывает, какую
часть амплитуды падающей волны в конце линии составляет
амплитуда отраженной волны

18.

Амплитуда отраженной волны тока в линии
I 2 ОТР
U 2 ОТР
U
ZB
U 2 ПАД
U I 2 ОТР ;
ZB
I 2 ОТР I I 2 ПАД
I U
Коэффициент отражения
значению и противоположен
отражения по напряжению
по току равен по
по знаку коэффициенту
Короткозамкнутая линия на конце ZH = 0
U 1
I 1
Падающая и отраженная волны напряжения в конце линии
имеют равные амплитуды и сдвинуты по фазе по отношению
друг другу на 180º. Амплитуда результирующей волны
напряжения в конце линии будет равна нулю. В тоже время
падающая и отраженная волны тока будут иметь равные
амплитуды, что приведет к увеличению вдвое тока в конце
короткозамкнутой линии
Холостой ход в конце линии ZH = ( U= 1, I= -1) – «противоположное»

19.

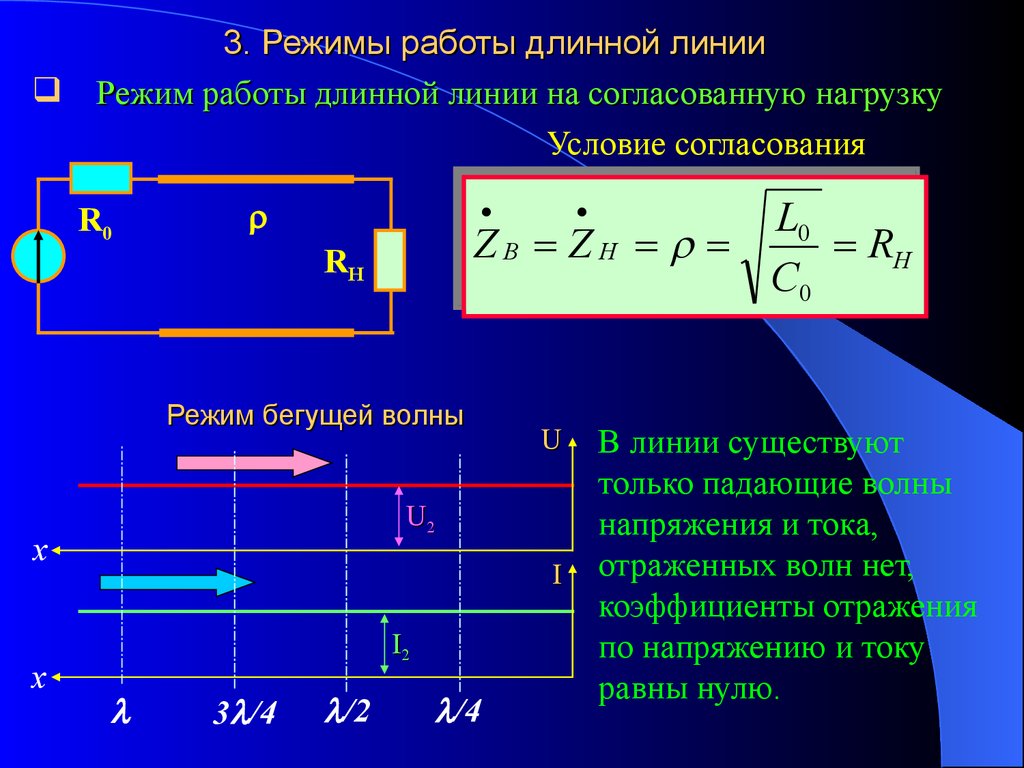
3. Режимы работы длинной линии
Режим работы длинной линии на согласованную нагрузку
Условие согласования
R0
LL00
ZZВВ ZZНН
RRНН
CC00
RH
Режим бегущей волны
U
U2
x
x
I
I2
3 /4
/2
/4
В линии существуют
только падающие волны
напряжения и тока,
отраженных волн нет,
коэффициенты отражения
по напряжению и току
равны нулю.

20.

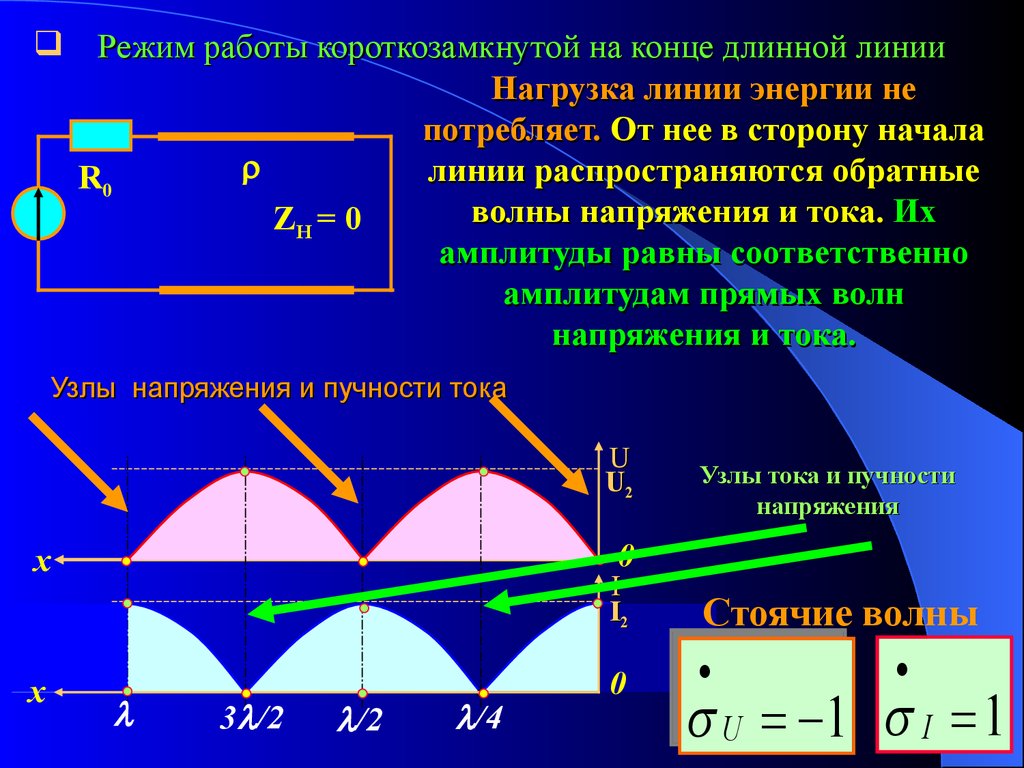
Режим работы короткозамкнутой на конце длинной линии
Нагрузка линии энергии не
потребляет. От нее в сторону начала
линии распространяются обратные
R0
волны напряжения и тока. Их
ZH = 0
амплитуды равны соответственно
амплитудам прямых волн
напряжения и тока.
Узлы напряжения и пучности тока
U
U2
0
x
x
Узлы тока и пучности
напряжения
I
I2
3 /2
/2
/4
0
Стоячие волны
UU 11 I 1

21.

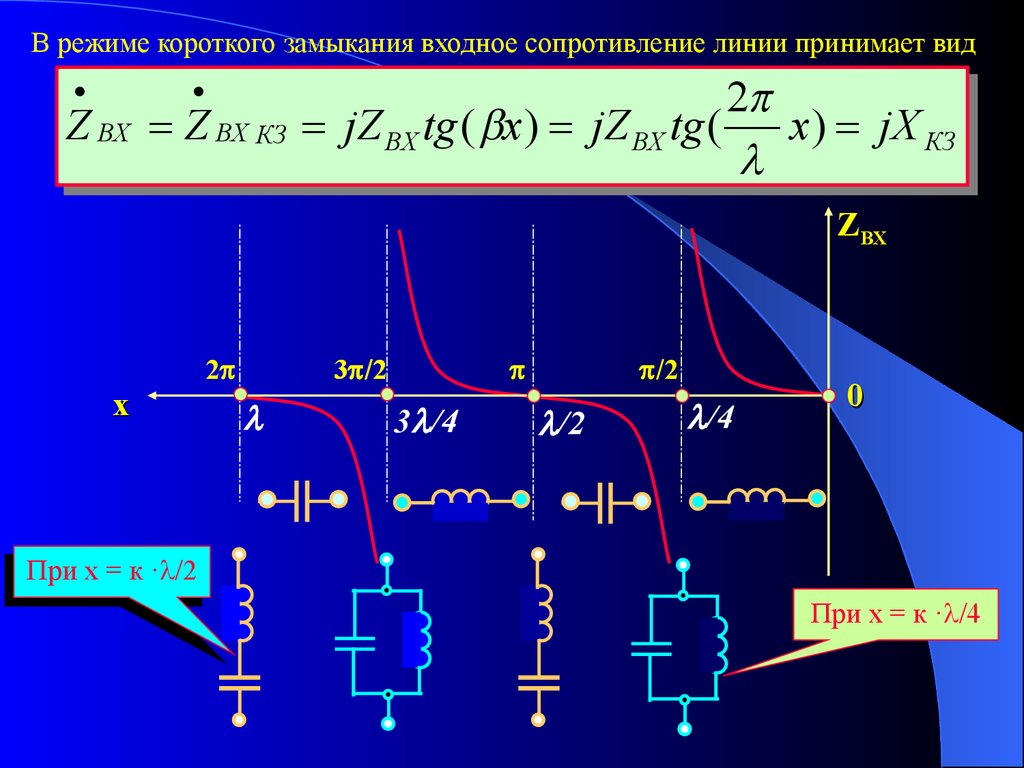
В режиме короткого замыкания входное сопротивление линии принимает вид
22
ZZBX
tg ( x) jZ BXtg
ZZBX
jZ
jZBX
tg(( xx)) jX
jXКЗКЗ
BX
BXКЗ
КЗ
BX tg ( x ) jZBX
ZBX
x
2
3 /2
3 /4
/2
/2
/4
0
Прихх==кк· /2
· /2
При
При х = к · /4

22.

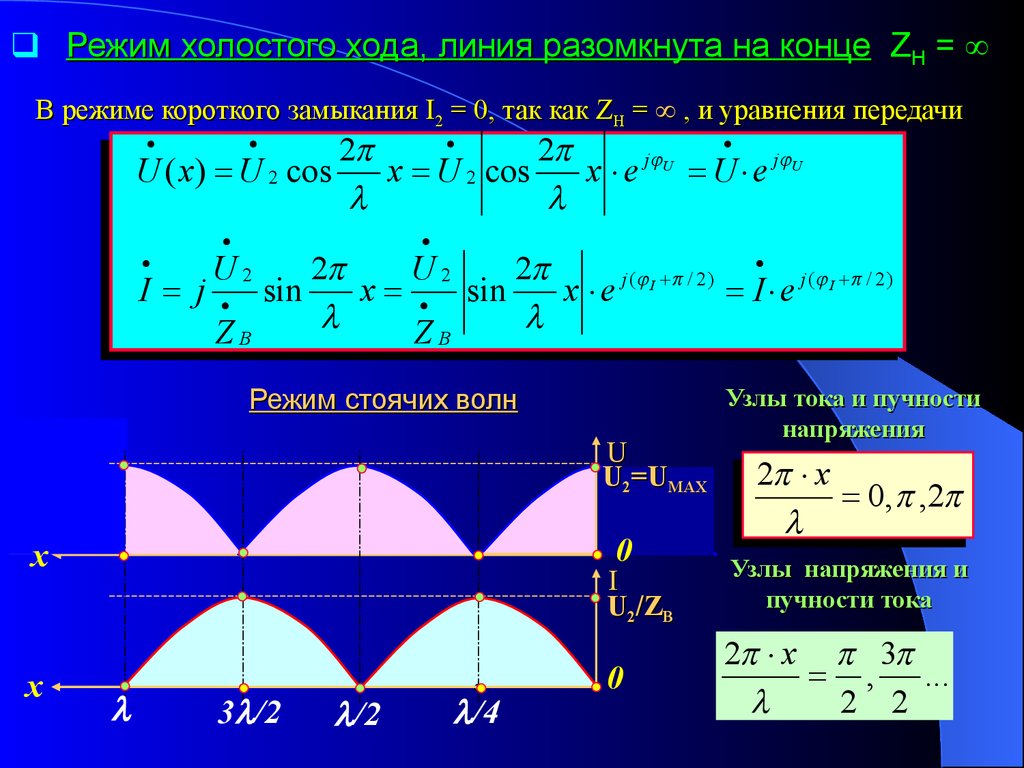
Режим холостого хода, линия разомкнута на конце ZH =
В режиме короткого замыкания I2 = 0, так как ZH = , и уравнения передачи
2
2
j U
U ( x) U 2 cos
x U 2 cos
x e U e j U
2
U2
2
j ( I / 2 )
I j sin
x sin
x e
I e j ( I / 2 )
ZB
ZB
U2
Режим стоячих волн
U
U2=UMAX
0
x
x
3 /2
/2
/4
Узлы тока и пучности
напряжения
2 х
0, ,2
I
U2/ZB
Узлы напряжения и
пучности тока
0
2 х 3
, ...
2 2

23.

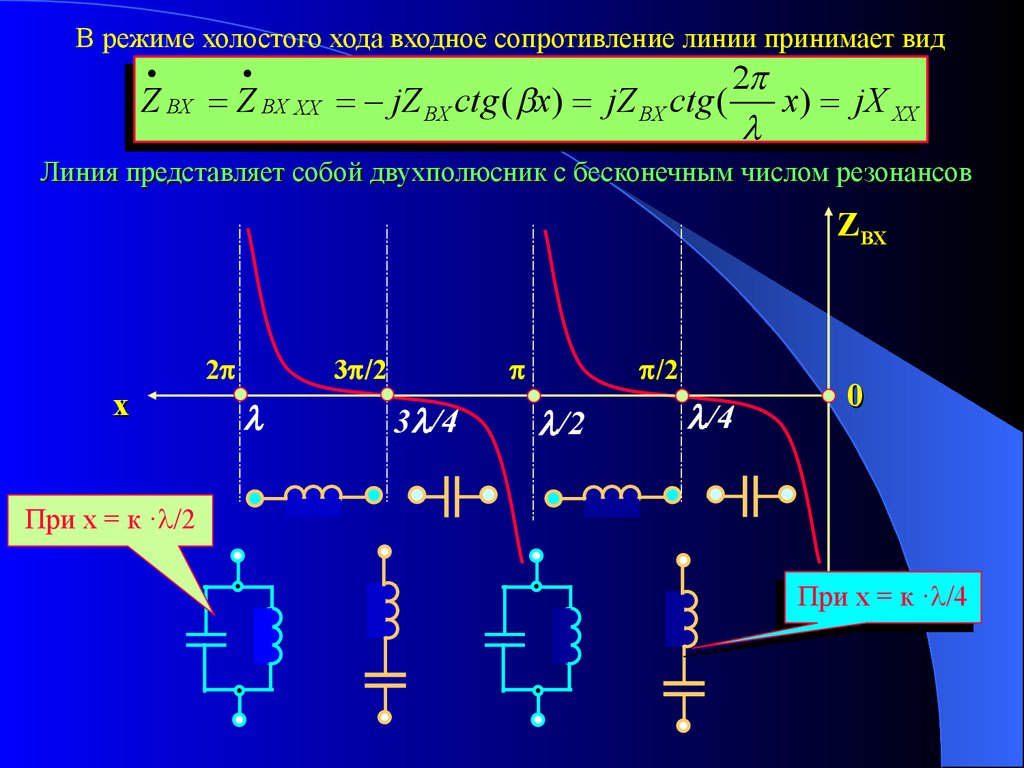
В режиме холостого хода входное сопротивление линии принимает вид
Z BX Z BX ХХ
2
jZ BX сtg ( x) jZ BX сtg (
x) jX ХХ
Линия представляет собой двухполюсник с бесконечным числом резонансов
ZBX
x
2
3 /2
3 /4
/2
/2
/4
0
При х = к · /2
Прихх==кк· /4
· /4
При

24.

Режим работы на несогласованную
нагрузку ZH ZB
2
Z
2
B
U ( x) U 2 cos
x j sin
x
Z
H
1
2
1
2
I ( x) U 2 cos
x j sin
Z H
ZB
Режим работы смешанных волн
x
U
UMAX
UMIN
0
I
IMAX
I
x
2
x
k БВ
U min
U max
/4
3 /
/2
4
U ПР U ОБР
I min
0 k БВ 1
U ПР U ОБР
I max
IMIN
0
Количественная
степень согласования
линии с нагрузкой

25.

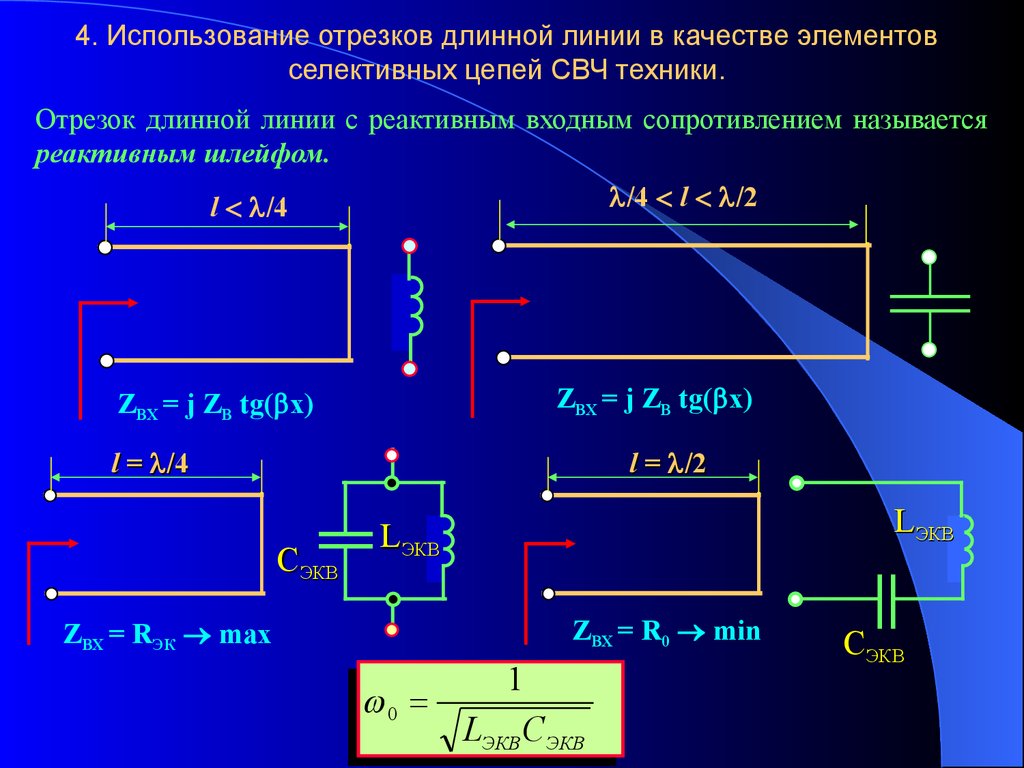
4. Использование отрезков длинной линии в качестве элементов
селективных цепей СВЧ техники.
Отрезок длинной линии с реактивным входным сопротивлением называется
реактивным шлейфом.
/4 l /2
l /4
ZВХ = j ZB tg( x)
ZВХ = j ZB tg( x)
l = /4
l = /2
CЭКВ
LЭКВ
LЭКВ
ZВХ = R0 min
ZВХ = RЭК max
0
1
LЭКВ СЭКВ
CЭКВ

26.

Металлический изолятор.
При l = /4 входное сопротивление
отрезка линии обращается в
бесконечность (изолятор для
подвески воздушных фидерных
линий).
Воздушная
двухпроводная линия
/4
Заземлитель
Линейный вольтметр:
/4
Непосредственное включение в цепь
измерительного прибора при очень
высокой частоте нарушает режим
работы ЭЦ, так как вносит добавочное
реактивное и активное сопротивление.
Подключение измерительного прибора к отрезку линии практически создает
короткое замыкание. Входное сопротивление линейного вольтметра
оказывается очень большим, и он не оказывает заметного влияния на цепь, в
которой измеряется напряжение.
U I при l / 4

27.

Полосовой фильтр
/2
/4
ZВ
Z ВХ ТР Z B
Четвертьволновый трансформатор сопротивлений
(согласующий трансформатор)
Согласующее устройство
l = /4
использует свойство отрезка
линии трансформировать
ZТР
сопротивление нагрузки к
RH
волновому сопротивлению линии
Пример: Для согласования нагрузки RH =50 Ом и линии с
2
волновым сопротивлением ZB = 75 Ом потребуется
Z ТР
/ RH
четвертьволновый отрезок …
Z ТР Z В RH
Z ТР 75 50 3750 61,2Ом

28.

Задание на самостоятельную работу
Литература:
Литература
1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории
цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 169 –187.
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 235 –
244.
3. Фрикс В.В. Основы теории цепей: Учебное пособие для межвузовского
использования вузов, - М.: Радио Софт, 2002 г, с. 221 –228.