Похожие презентации:
Установившиеся режимы в цепях с распределенными параметрами
1. Лекция № 2
Лекционные презентациипо курсу ТОЭ
«Установившиеся режимы в
цепях с распределенными
параметрами»
Лекция № 2
В лекции рассматриваются установившиеся
режимы в однородных линиях с
распределенными параметрами. Даны
основные характеристики бегущей волны,
рассмотрена методика расчета токов и
напряжений в однородных линиях во
временной форме (вещественной области)
при синусоидальном напряжении источника.
MП
1
2. Линии с распределенными параметрами
Лекция № 2Линии с распределенными параметрами
Токи и напряжения в линиях с распределенными параметрами
оказываются функцией двух координат u ( x, t ), i ( x, t ) :
временной – времени t и пространственной – координаты
(длины) x, отсчитываемой вдоль выбранного направления.
Уравнения, описывающие процессы в линии, будут
уравнениями в частных производных. Можно считать
распределение параметров равномерным, если взаимное
расположение, сечение проводов, параметры сред не
изменяются вдоль линии. Такая линия называется однородной.
Такое рассмотрение является идеализацией процесса.
MП
2
3. Общее решение уравнений однородной линии в комплексной форме
Лекция № 2Общее решение уравнений однородной
линии в комплексной форме
При расчете установившихся режимов при
синусоидальном напряжении источника заданной
частоты 2 f используют комплексный метод
расчета: i( x, t ) I ( x) u ( x, t ) U ( x)
Обозначим: Z 0 R 0 j L0 – комплексное сопротивление
на единицу длины,Y0 G 0 j C0 – комплексная
проводимость на единицу длины.
Уравнение однородной линии
MП
2
dU
Z 0Y0U ( x)
2
dx
2
3
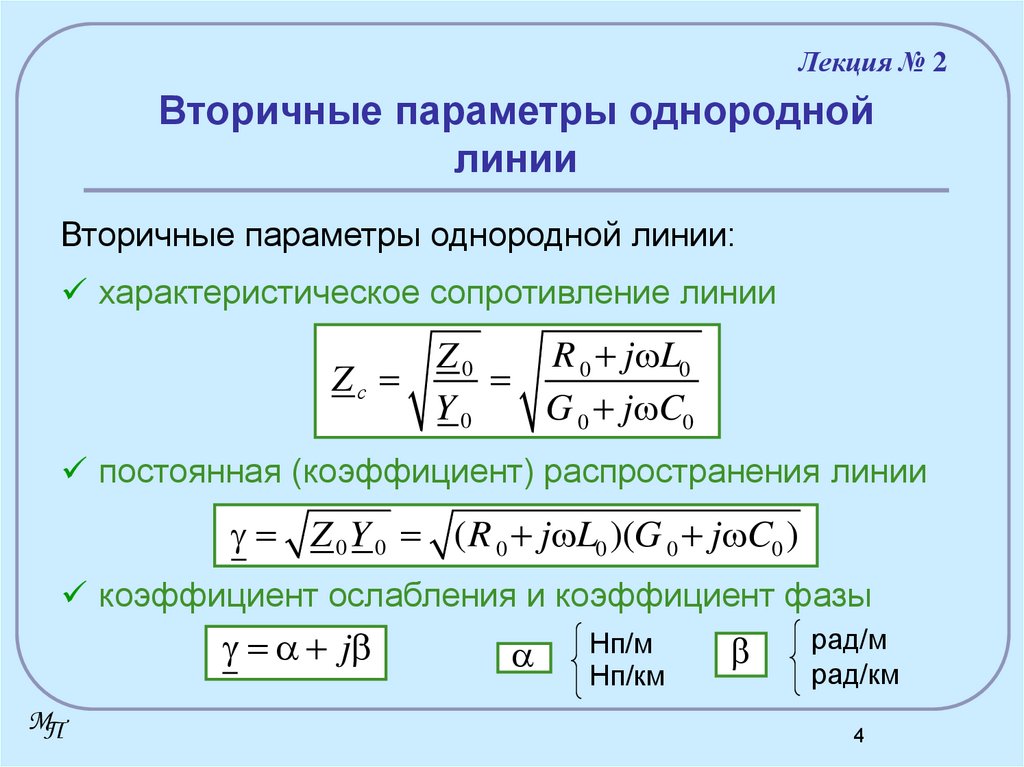
4. Вторичные параметры однородной линии
Лекция № 2Вторичные параметры однородной
линии
Вторичные параметры однородной линии:
характеристическое сопротивление линии
R 0 j L0
Z0
Zс
Y0
G 0 j C0
постоянная (коэффициент) распространения линии
Z 0 Y 0 ( R 0 j L0 )(G 0 j C0 )
коэффициент ослабления и коэффициент фазы
j
MП
Нп/м
Нп/км
рад/м
рад/км
4
5. Решение уравнений однородной линии в комплексной форме
Лекция № 2Решение уравнений однородной линии в
комплексной форме
Решение может быть найдено как сумма прямых и
обратных волн:
U ( x) U пр ( x) U обр ( x)
I ( x) Iпр ( x) Iобр ( x)
U пр ( x) Z c Iпр ( x)
Замечание: введение понятия
прямых и обратных волн
облегчает анализ процессов
MП
U обр ( x) =Z c Iобр ( x)
5
6. Решение уравнений однородной линии в комплексной форме
Лекция № 2Решение уравнений однородной линии в
комплексной форме
Для прямых и обратных волн при отсчете xот начала
линии
Решение для отдельных
составляющих при отсчете x
от начала линии:
U пр ( x) A1e x A1e xe j x
U обр ( x) A2e x A2e xe j x
MП
j 1
U ( x) U пр ( x) U обр ( x)
A1 A1e
I ( x) Iпр ( x) Iобр ( x)
A2 A2e
j 2
комплексные
постоянные
интегрирования
6
7. Решение уравнений однородной линии в комплексной форме
Лекция № 2Решение уравнений однородной линии в
комплексной форме
Для прямых и обратных волн при отсчете x от начала
линии
Для U ( x), I ( x) :
U1 I1Z с
U1 I1Z с U
U1пр
1обр
2
2
U пр ( x) U1прe
Iпр ( x)
Дано: U1 , I1 , Z c , , l
MП
x
U пр ( x)
U обр U1обрe
Iобр (x) =
x
U обр (x)
Zc
Zc
U ( x) U пр ( x) U обр ( x)
I ( x) Iпр ( x) Iобр ( x)
7
8. Решение уравнений однородной линии во временной форме
Лекция № 2Решение уравнений однородной линии
во временной форме
Переход в вещественную (временную) область дает
решение для мгновенных значений ( Z c Z c e j )
u ( x, t ) 2 A1e x sin( t x 1 ) 2 A2e x sin( t x 2 )
uпр ( x, t )
uобр ( x, t )
A1 x
A2 x
i ( x, t ) 2 e sin( t x 1 ) 2 e sin( t x 2 )
Zc
Zc
iпр ( x, t )
iобр ( x, t )
Для прямых и обратных волн при отсчете x от начала линии
MП
8
9. Бегущая волна
Лекция № 2Бегущая волна
Каждое слагаемое определяет бегущую волну
uпр ( x, t ) 2 A1e x sin( t x 1 )
A1 x
iпр ( x, t ) 2 e sin( t x 1 )
Zc
прямая волна (движение
в направлении
возрастания координаты)
uобр ( x, t ) 2 A2e x sin( t x 2 )
A2 x
iобр ( x, t ) 2 e sin( t x 2 )
Zc
обратная волна
(движение
в направлении
убывания координаты)
x
Для прямых и обратных волн при отсчете x от начала линии
MП
9
10. Бегущая волна
Лекция № 2Бегущая волна
Каждое из слагаемых в любой фиксированной x
координате представляет собой периодическую
функцию времени, т.е. описывает простые
гармонические колебания с частотой, определяемой
частотой источника . Любое колебание определяется
амплитудой и фазой. Так как рассматриваемая линия
с потерями, то по мере распространения колебаний
вдоль линии часть электромагнитной энергии
поглощается и амплитуда колебаний убывает по
экспоненциальному закону.
MП
10
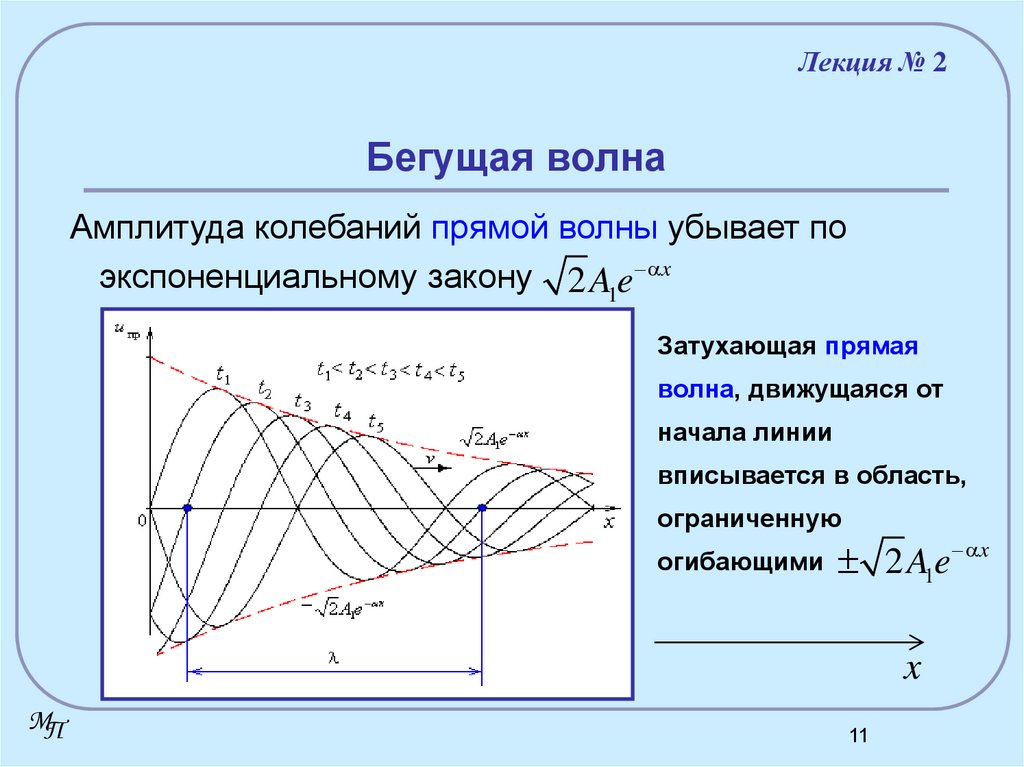
11. Бегущая волна
Лекция № 2Бегущая волна
Амплитуда колебаний прямой волны убывает по
экспоненциальному закону 2 A1e x
Затухающая прямая
волна, движущаяся от
начала линии
вписывается в область,
ограниченную
огибающими
2 A1e x
x
MП
11
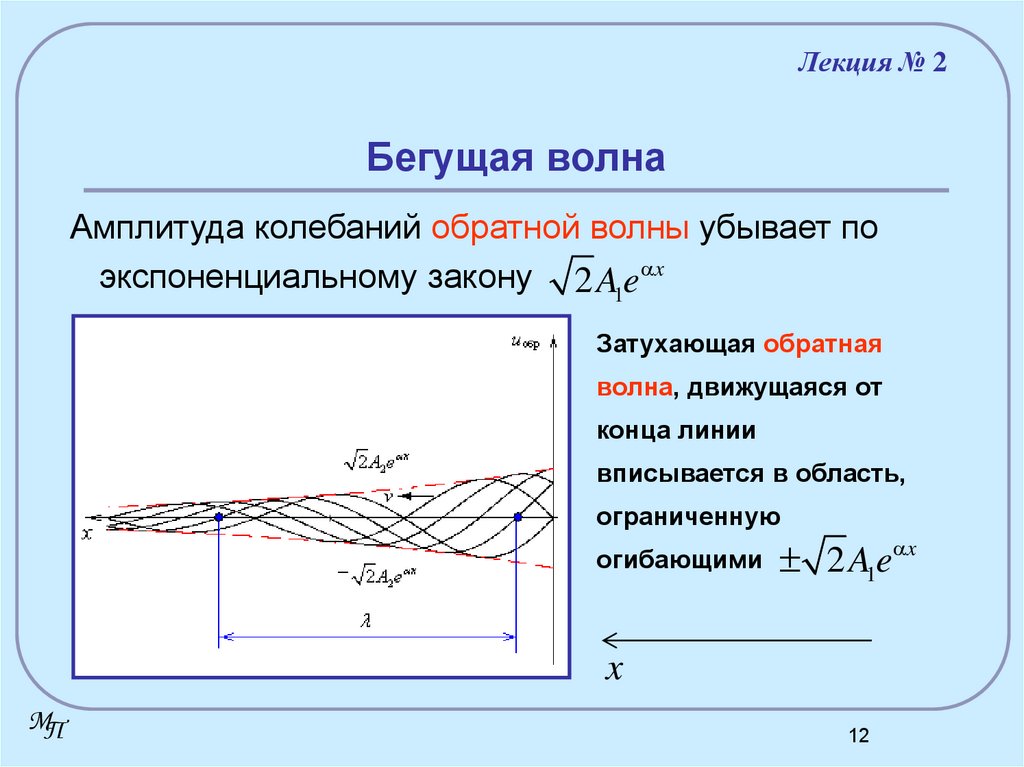
12. Бегущая волна
Лекция № 2Бегущая волна
Амплитуда колебаний обратной волны убывает по
экспоненциальному закону 2 A1e x
Затухающая обратная
волна, движущаяся от
конца линии
вписывается в область,
ограниченную
огибающими
2 A1e x
x
MП
12
13. Основные характеристики бегущей волны
Лекция № 2Основные характеристики бегущей
волны
Основными характеристиками бегущей волны являются
фазовая скорость и длина волны. Фазовой
скоростью волны v называется скорость
перемещения фиксированной фазы колебания,
перемещаясь с которой фаза остается постоянной,
т.е. t x 1 const
d
( t x 1 ) 0
dt
MП
dx
v
dt
13
14. Основные характеристики бегущей волны
Лекция № 2Основные характеристики бегущей
волны
Длиной волны λ называется расстояние между
ближайшими двумя точками, колеблющимися в одной
фазе. Расстояние берется в направлении движения
волны, для прямой и обратной волны λ
определяется из соотношения
t ( x ) 1 t x 1 2
или t ( x ) 1 t x 1 2 .
Следовательно,
MП
2
14
15. Основные характеристики бегущей волны
Лекция № 2Основные характеристики бегущей
волны
Длина волны λ зависит от частоты и фазовой скорости
2 v
f
При этом изменение фазы по длине линии составит
l
(«фазовый набег»). Это изменение фазы будет
существенно влиять на процессы в линии, если будет
l соизмерим с 2 .
MП
15
16. Основные характеристики бегущей волны
Лекция № 2Основные характеристики бегущей
волны
Изменение фазы будет существенно влиять на процессы
в линии, если длина линии будет соизмерима с длиной
волны.
На разных частотах длина волны
разная, поэтому линия длиной l
может быть рассмотрена и как цепь
с распределенными параметрами,
если l соизмерима с λ, и как цепь
с сосредоточенными параметрами,
если l << λ.
MП
16
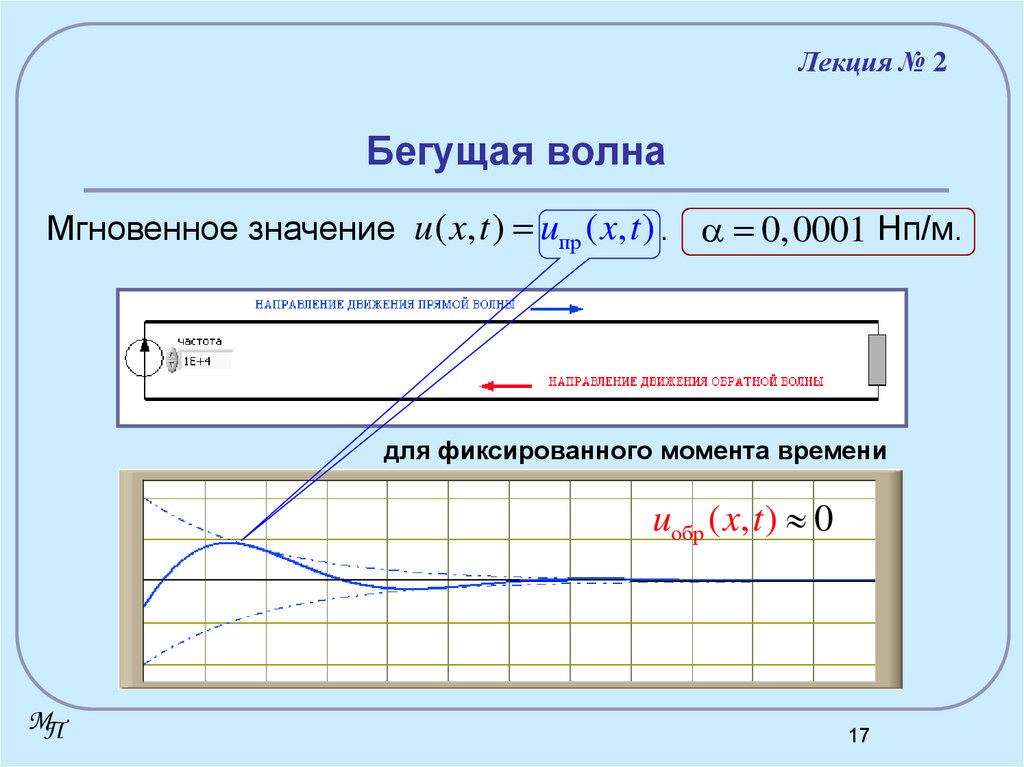
17. Бегущая волна
Лекция № 2Бегущая волна
Мгновенное значение u ( x, t ) uпр ( x, t ) . 0,0001 Нп/м.
для фиксированного момента времени
uобр ( x, t ) 0
MП
17
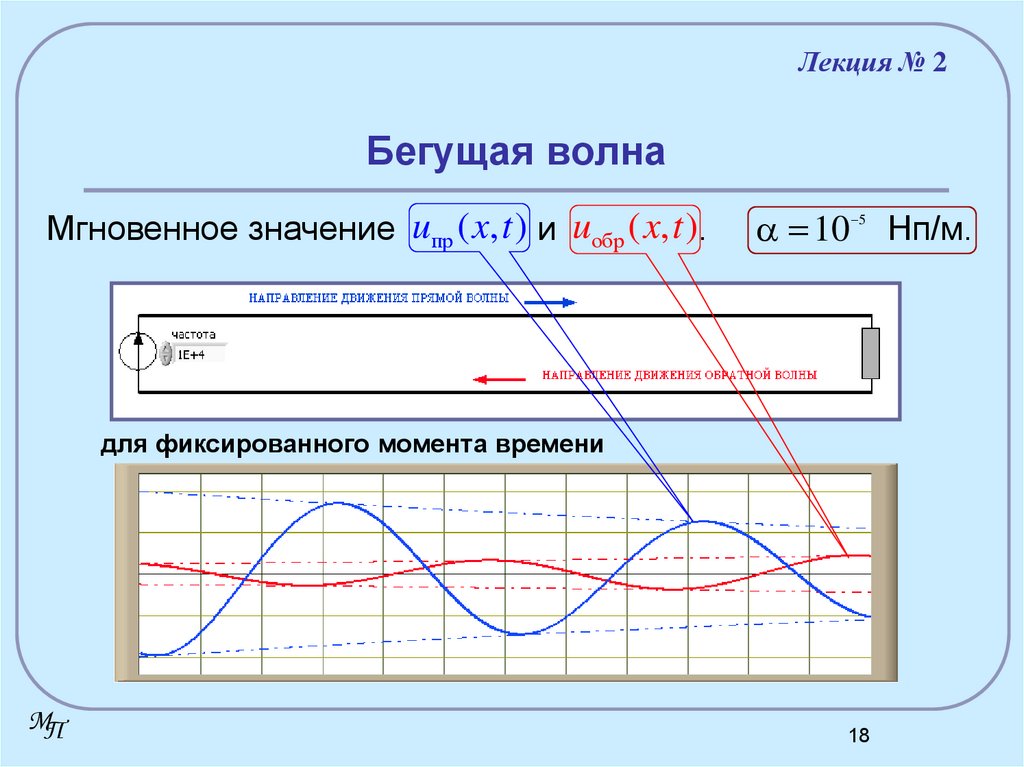
18. Бегущая волна
Лекция № 2Бегущая волна
Мгновенное значение uпр ( x, t ) и uобр ( x, t ).
10
5
для фиксированного момента времени
MП
18
Нп/м.
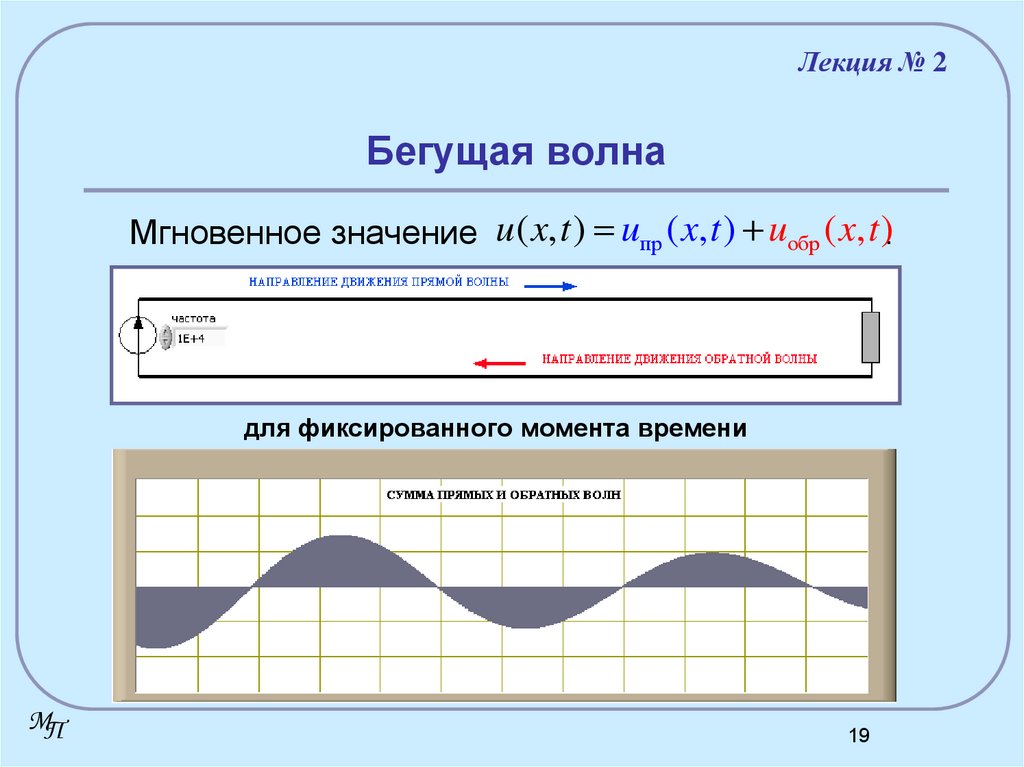
19. Бегущая волна
Лекция № 2Бегущая волна
Мгновенное значение u ( x, t ) uпр ( x, t ) uобр ( x, t ).
для фиксированного момента времени
MП
19













 Физика
Физика








