Похожие презентации:
Смежные углы и их свойства
1.
Смежные углы и их свойства.В
С
М
А
Два угла, у которых одна сторона общая,
а две другие являются продолжением одна другой,
называются смежными
Углы АМВ и СМВ – смежные.
Сумма смежных углов равна 1800
2.
Два угла называются вертикальными,если стороны одного угла являются
продолжениями сторон другого.
М
О
А
В
Углы АОВ и МОN являются
вертикальными.
N
Вертикальные углы равны
3.
Прямые MN и КР пересекаются в точке О,причем сумма углов КОМ и NОР равна 1340.
Найдите величину угла КОN.
M
O
K
1130
P
670
N
Тренировочные задания
4.
АВСНазовите сторону противолежащую
углу А; В; С.
В
Между какими сторонами заключены
углы А; В; С ?
Назовите углы, прилежащие к
стороне АВ; ВС; АС.
Назовите угол, противолежащий
к стороне АВ; ВС; АС.
А
С
5. Перпендикуляр к прямой
это отрезок, один конецкоторого лежит на данной
прямой, а сам он лежит на
прямой, перпендикулярной к
данной прямой.
1.АН а ;
2.А а ; Н а.
А
а
Н
6.
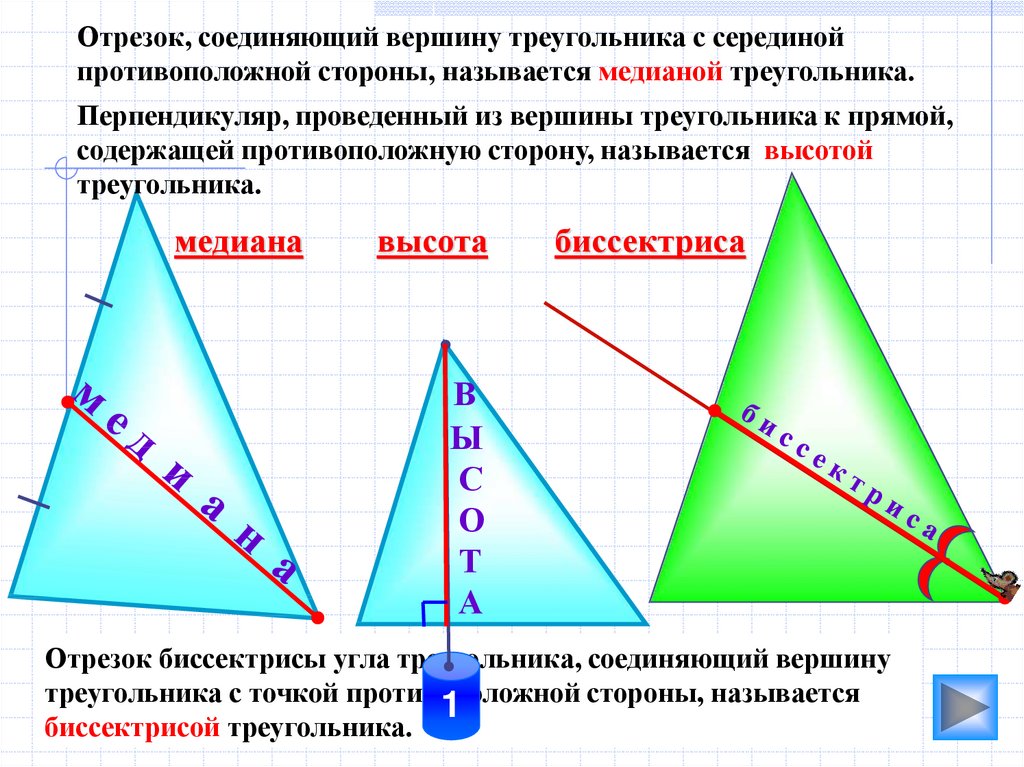
Отрезок, соединяющий вершину треугольника с серединойпротивоположной стороны, называется медианой треугольника.
Перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой
треугольника.
медиана
высота
биссектриса
В
Ы
С
О
Т
А
Отрезок биссектрисы угла треугольника, соединяющий вершину
треугольника с точкой противоположной стороны, называется
1
биссектрисой треугольника.
7.
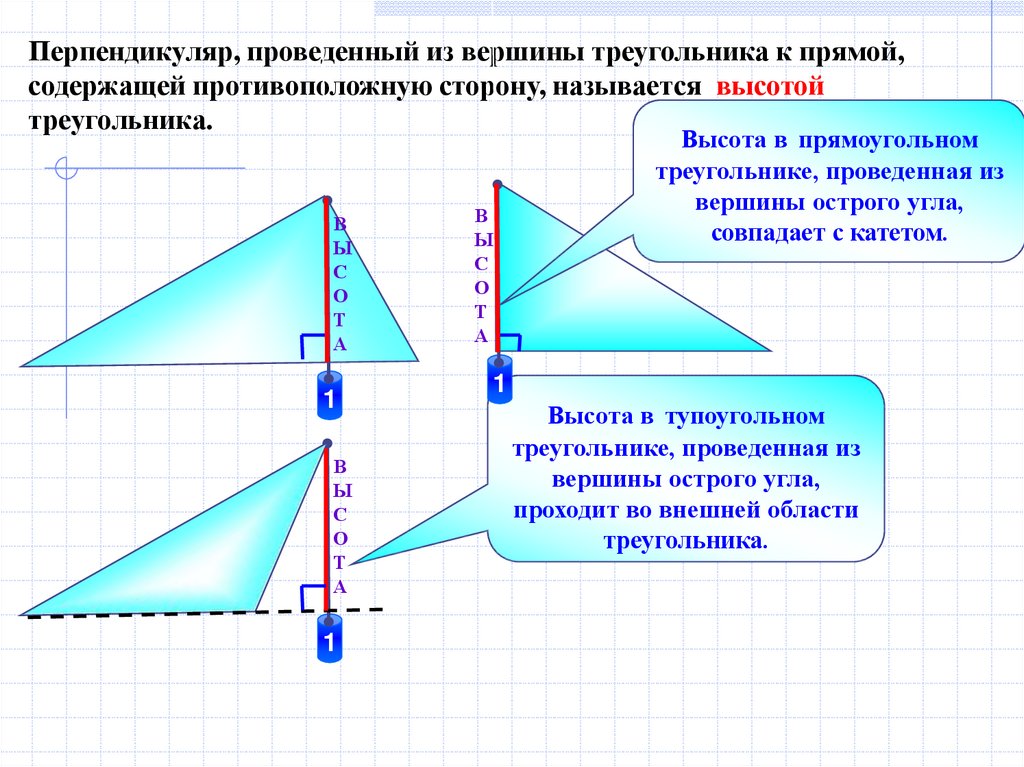
Перпендикуляр, проведенный из вершины треугольника к прямой,содержащей противоположную сторону, называется высотой
треугольника.
В
Ы
С
О
Т
А
1
В
Ы
С
О
Т
А
1
В
Ы
С
О
Т
А
Высота в прямоугольном
треугольнике, проведенная из
вершины острого угла,
совпадает с катетом.
1
Высота в тупоугольном
треугольнике, проведенная из
вершины острого угла,
проходит во внешней области
треугольника.
8.
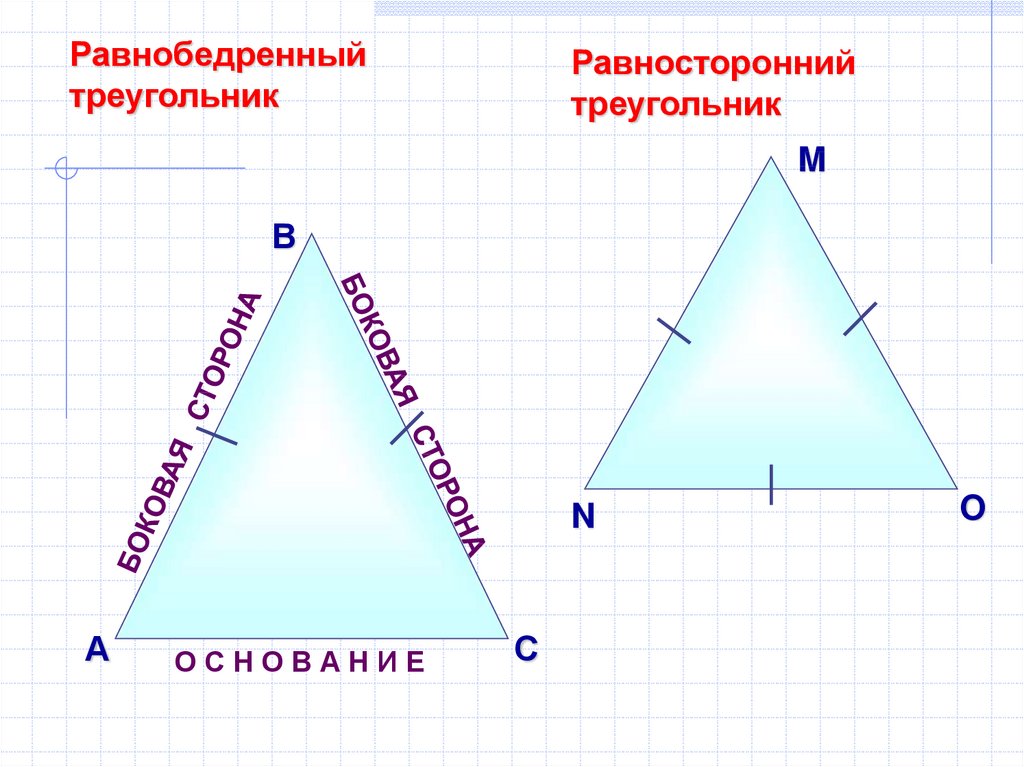
Равнобедренныйтреугольник
Равносторонний
треугольник
M
В
N
А
ОСНОВАНИЕ
С
O
9.
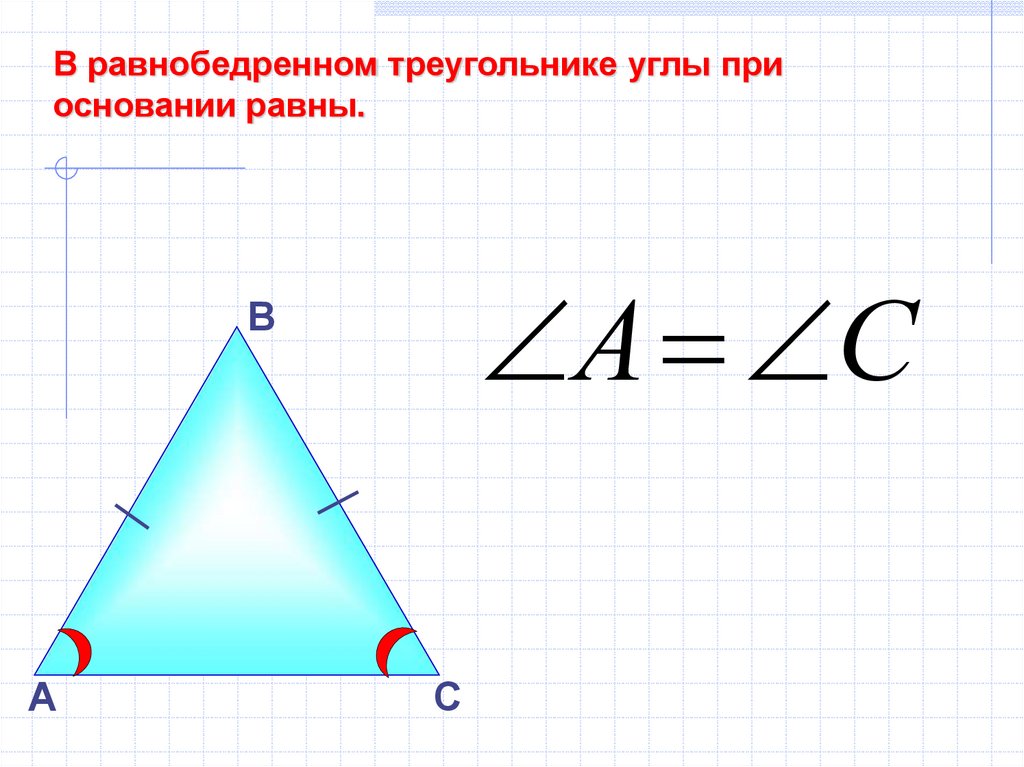
В равнобедренном треугольнике углы приосновании равны.
А С
В
А
С
10.
Тренировочные задания.D
DВА – ?
70
А
B
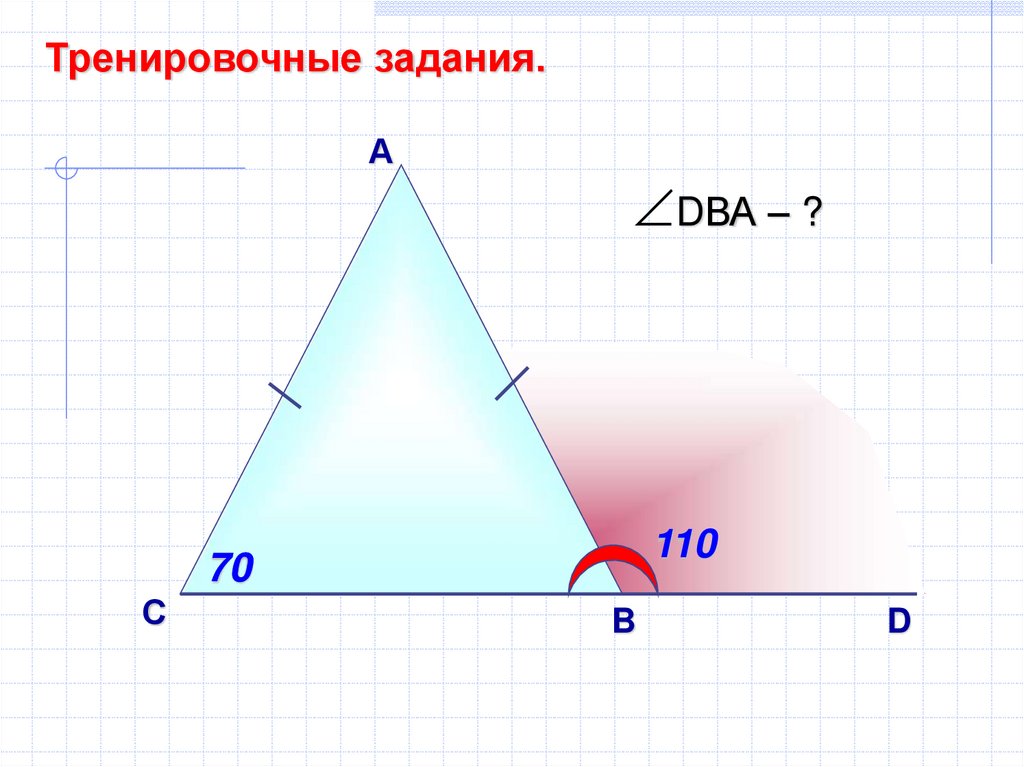
11.
Тренировочные задания.А
DВА – ?
110
70
С
B
D
12.
Тренировочные задания.А
D
DВА – ?
В
70
70
С
К
13.
В равнобедренном треугольнике биссектриса,проведенная к основанию, является медианой и высотой.
В
1 2
А
D
С
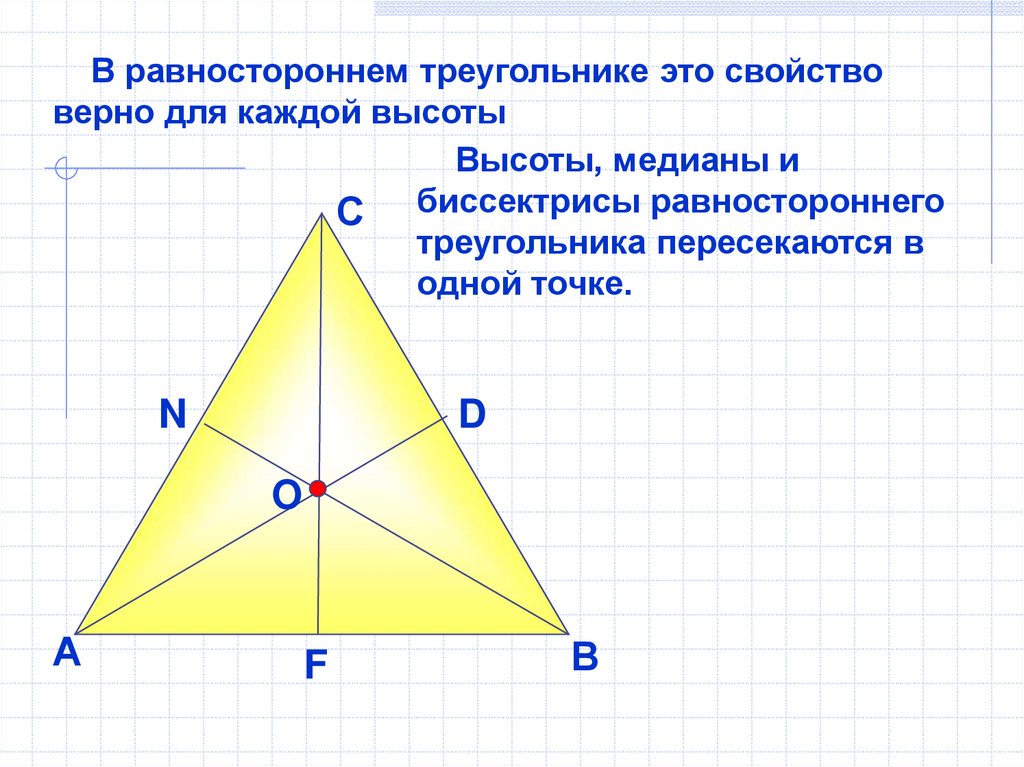
14.
В равностороннем треугольнике это свойствоверно для каждой высоты
Высоты, медианы и
С биссектрисы равностороннего
треугольника пересекаются в
одной точке.
N
D
O
А
F
В
15.
НайтиАВD
В
? 400
А
D
С
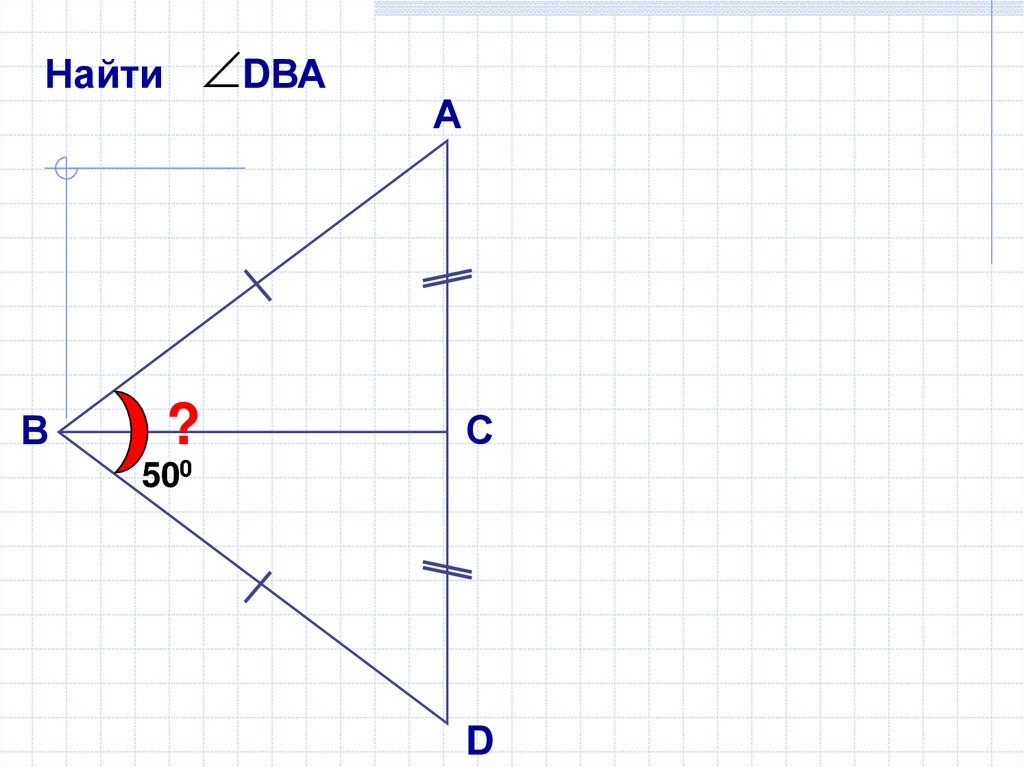
16.
DВАНайти
В
?
А
С
500
D
17.
НайтиАВD
А
D
?
В
600
30
С
М
К
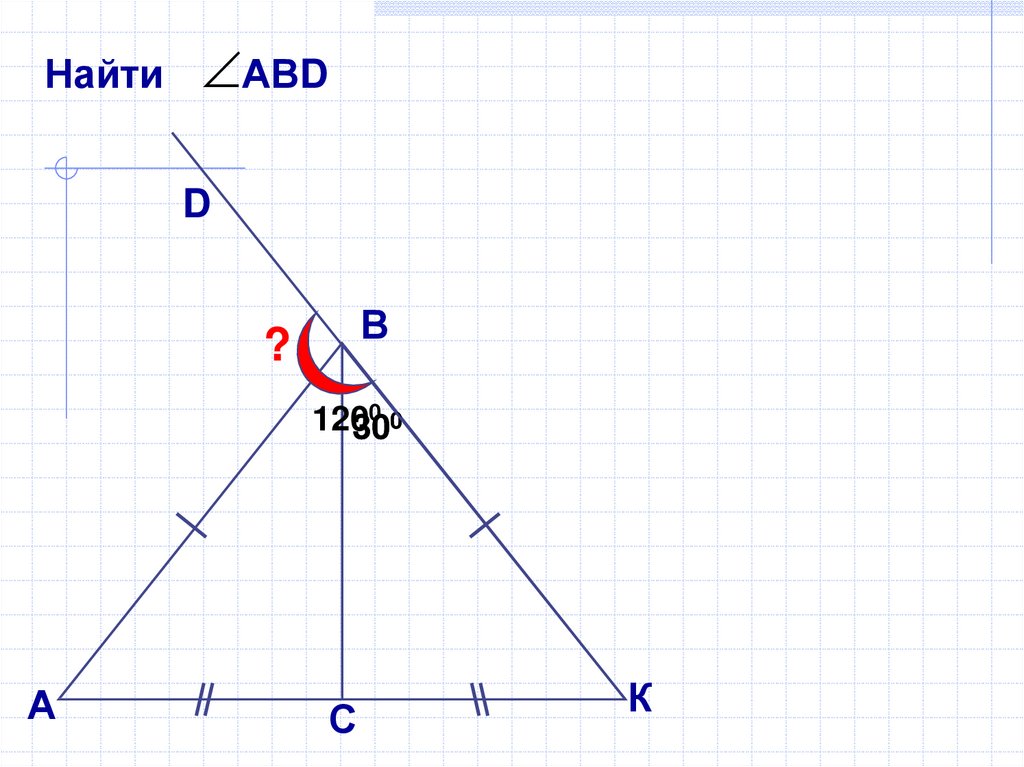
18.
НайтиАВD
D
В
?
00
12030
А
С
К
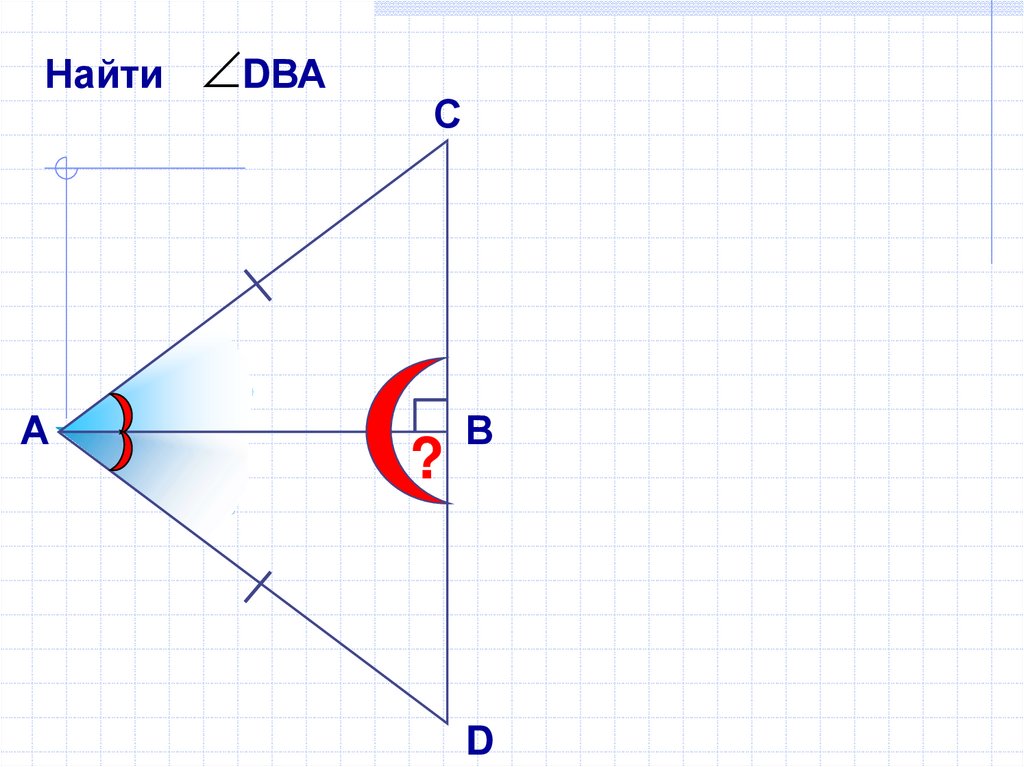
19.
НайтиА
DВА
С
?
В
D
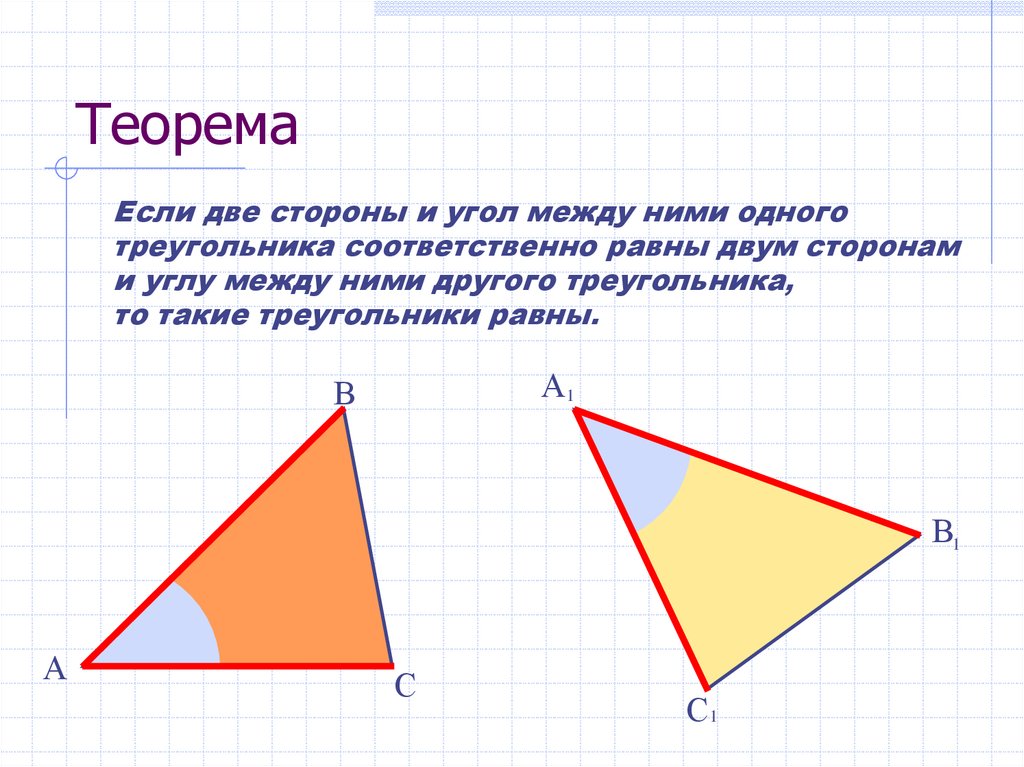
20. Теорема
Если две стороны и угол между ними одноготреугольника соответственно равны двум сторонам
и углу между ними другого треугольника,
то такие треугольники равны.
А1
В
В1
А
С
С1
21. Теорема
СА
В
А1
Если сторона и два прилежащих
к ней угла одного треугольника
соответственно равны стороне и
двум прилежащим к ней углам
другого треугольника,
то такие треугольники равны.
С1
В1
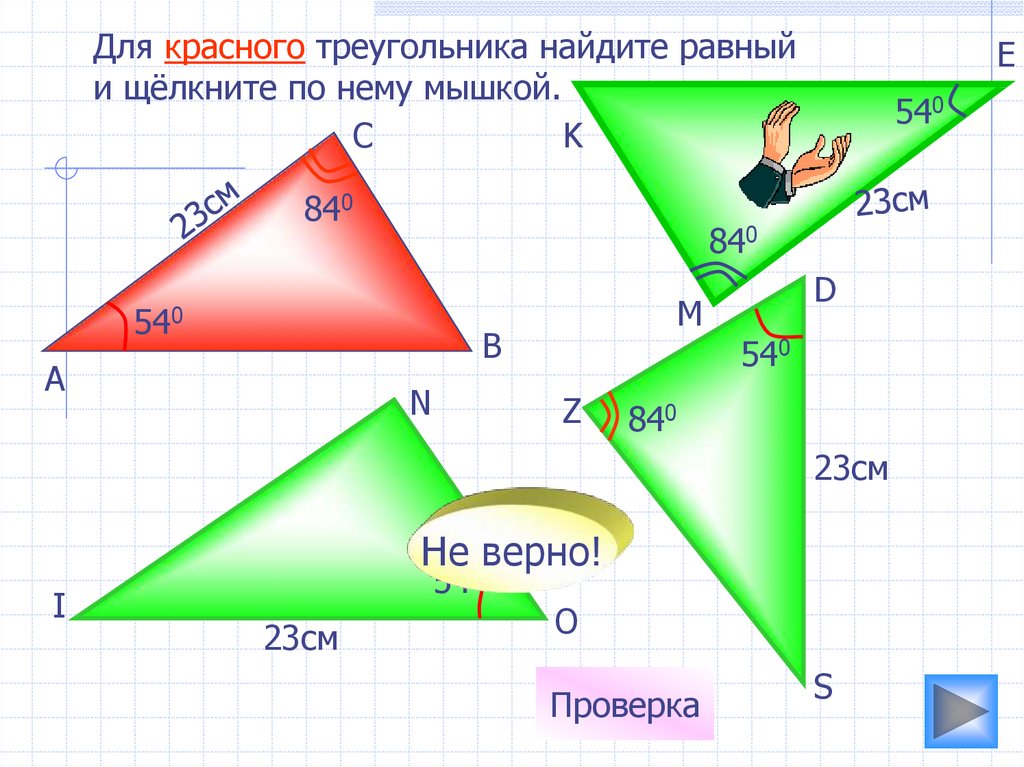
22.
Для красного треугольника найдите равныйи щёлкните по нему мышкой.
C
K
840
540
840
540
M
B
А
E
N
Z
D
540
840
23см
I
Не 0верно!
54
23см
O
Проверка
S
23. Теорема
Если три стороны одноготреугольника соответственно равны
трем сторонам другого треугольника,
то такие треугольники равны.
А1
С1
А
С
В
В1
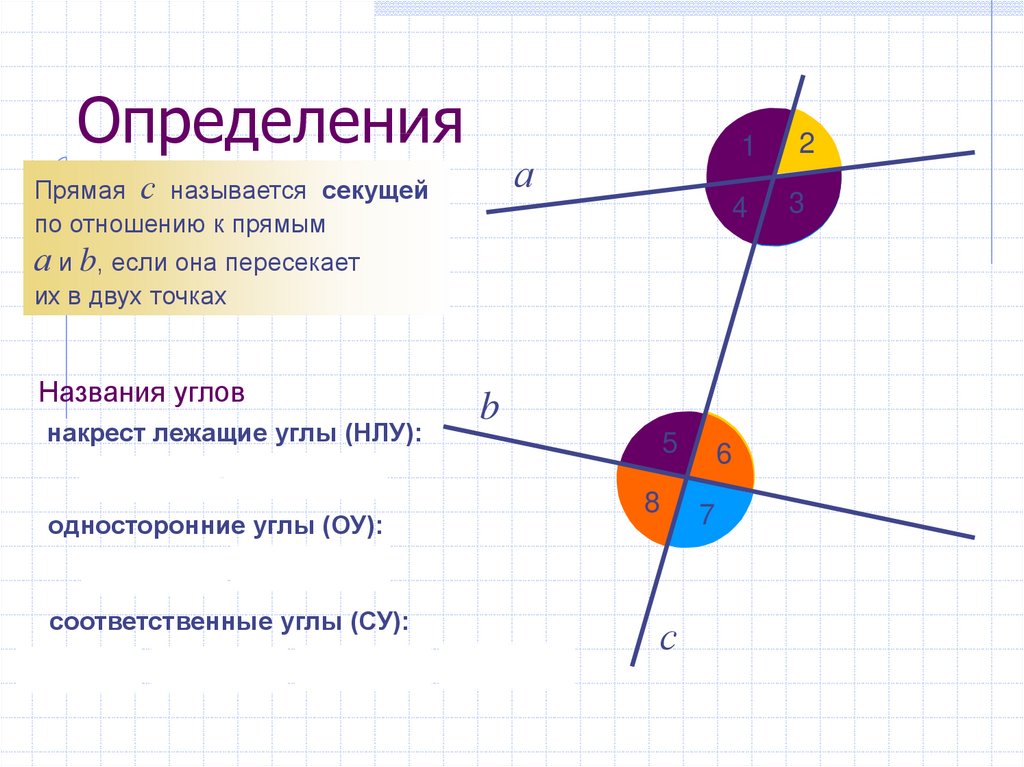
24. Определения
1а
Прямая с называется секущей
по отношению к прямым
4
а и b, если она пересекает
их в двух точках
Названия углов
накрест лежащие углы (НЛУ):
b
3 и 5, 4 и 6
односторонние углы (ОУ):
5
8
4 и 5, 3 и 6
соответственные углы (СУ):
1 и 5, 4 и 8, 2 и 6, 3 и 7
с
6
7
2
3
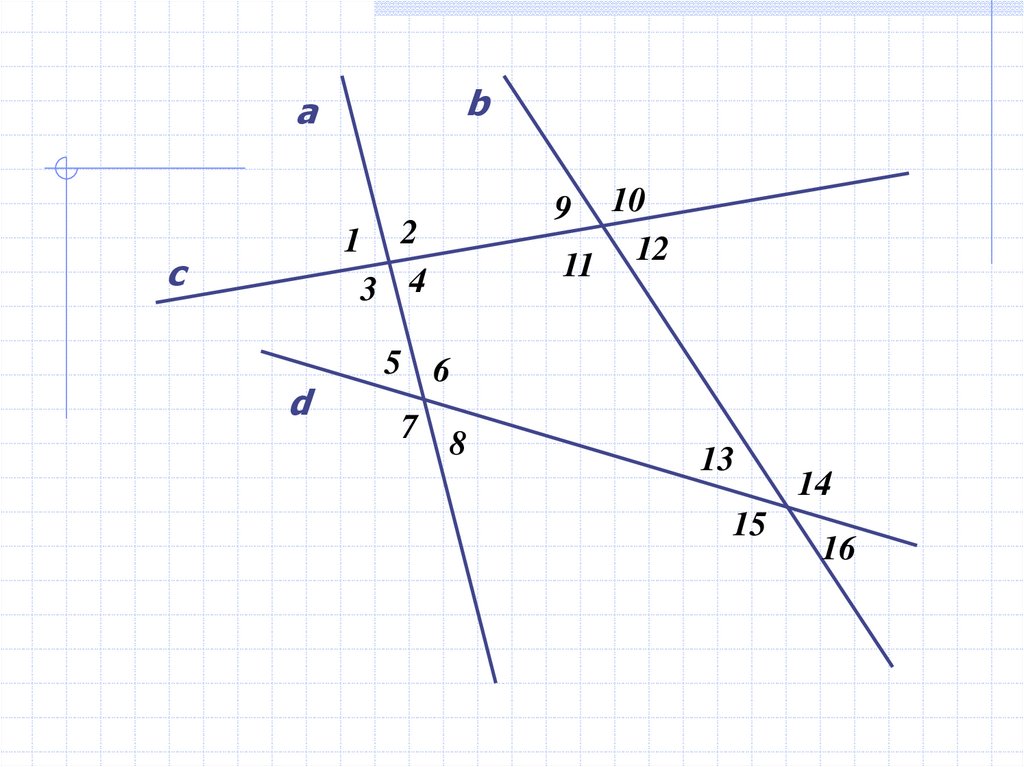
25.
bа
1 2
3 4
c
d
10
11 12
9
5 6
7 8
13
15
14
16
26.
BA
C
D
27.
BA
C
D
28.
BA
C
D
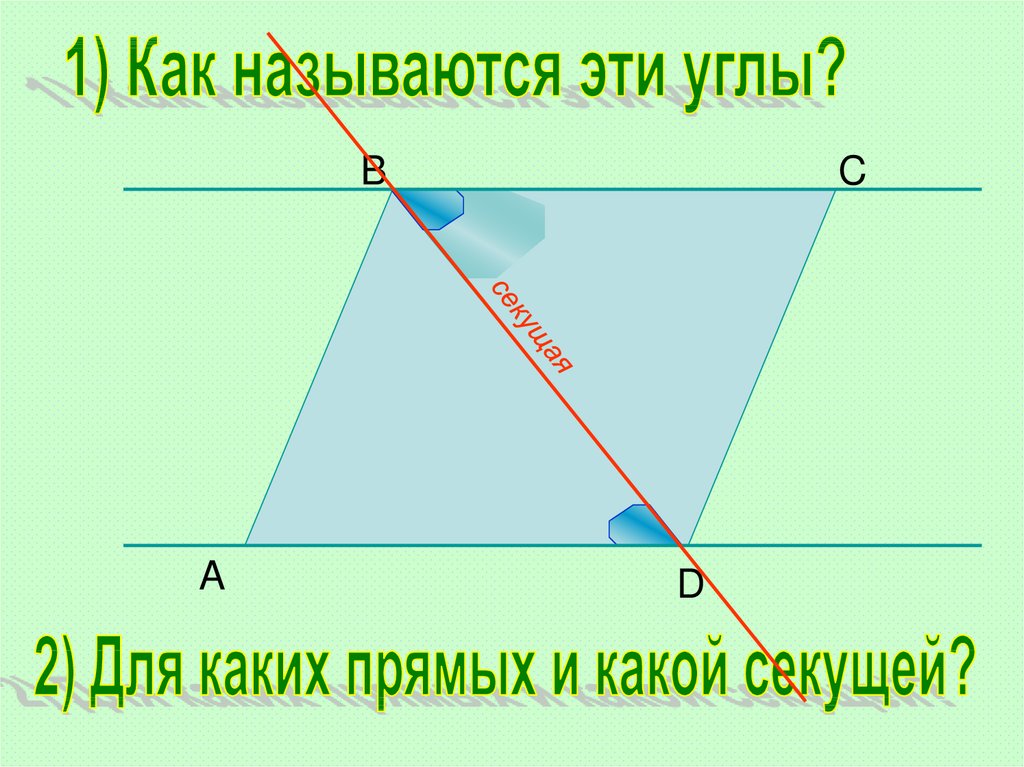
29.
BD
секущая
A
C
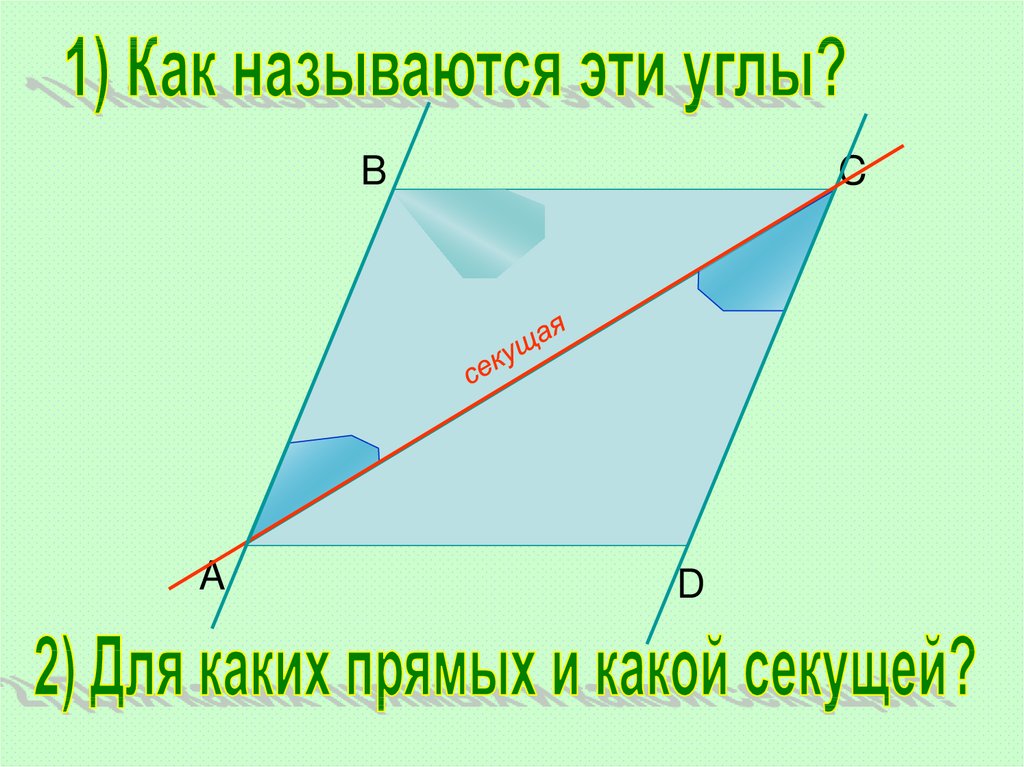
30.
BD
A
секущая
C
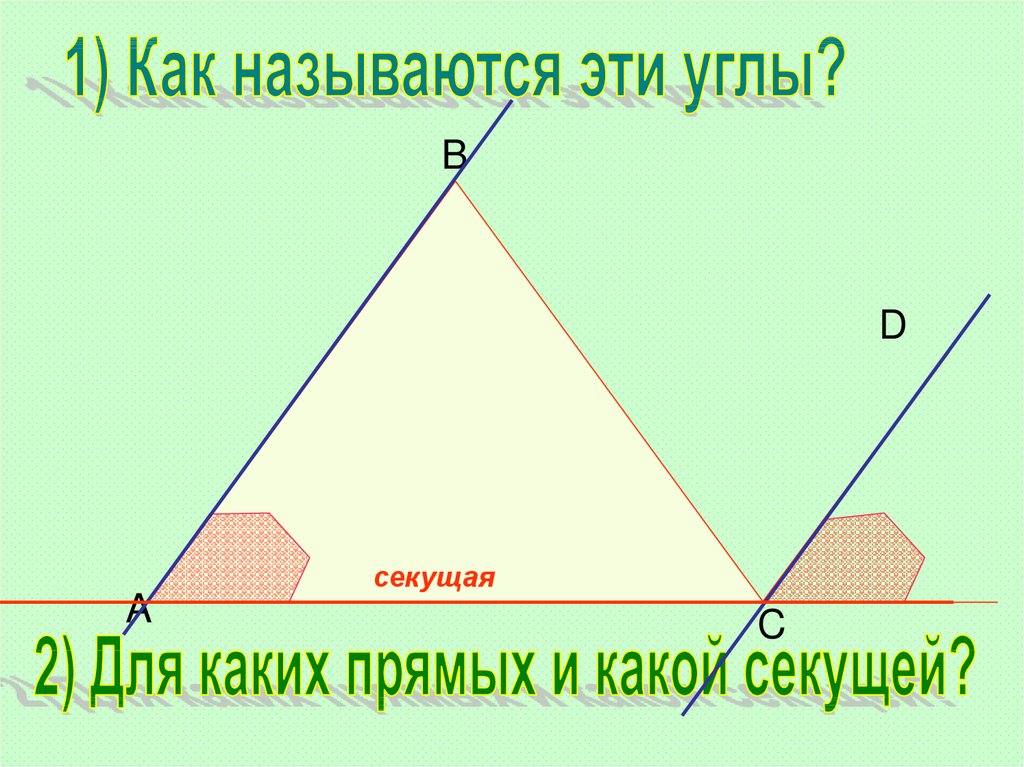
31.
BD
A
C
32.
аb
Определение.
аIIb
Две прямые на плоскости называются параллельными,
если они не пересекаются.
33.
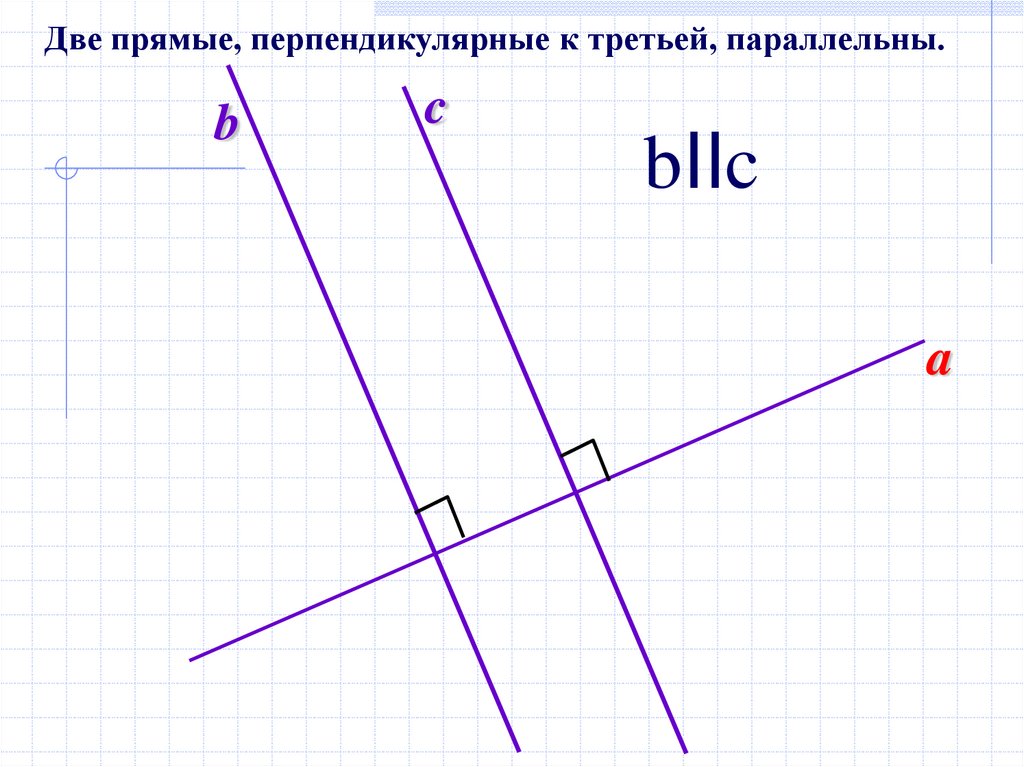
Две прямые, перпендикулярные к третьей, параллельны.b
c
bIIc
a
34.
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ.Если при пересечении двух прямых секущей
накрест лежащие углы равны, то прямые
параллельны.
c
460
460
a
aIIb
b
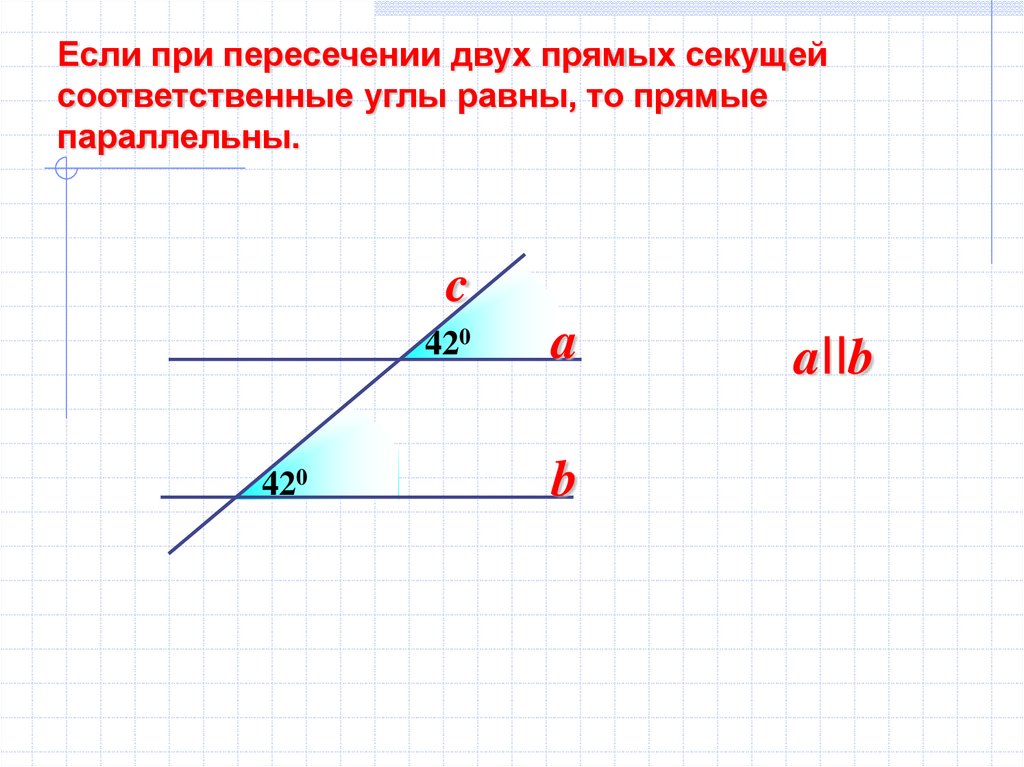
35.
Если при пересечении двух прямых секущейсоответственные углы равны, то прямые
параллельны.
c
420
420
a
b
aIIb
36.
Если при пересечении двух прямых секущей суммаодносторонних углов равна 1800, то прямые
параллельны.
c
a
1380
420
b
aIIb
37.
Задача 2B
47
A
0
45 0
C
46 0
45 0
D
Укажите параллельные
прямые
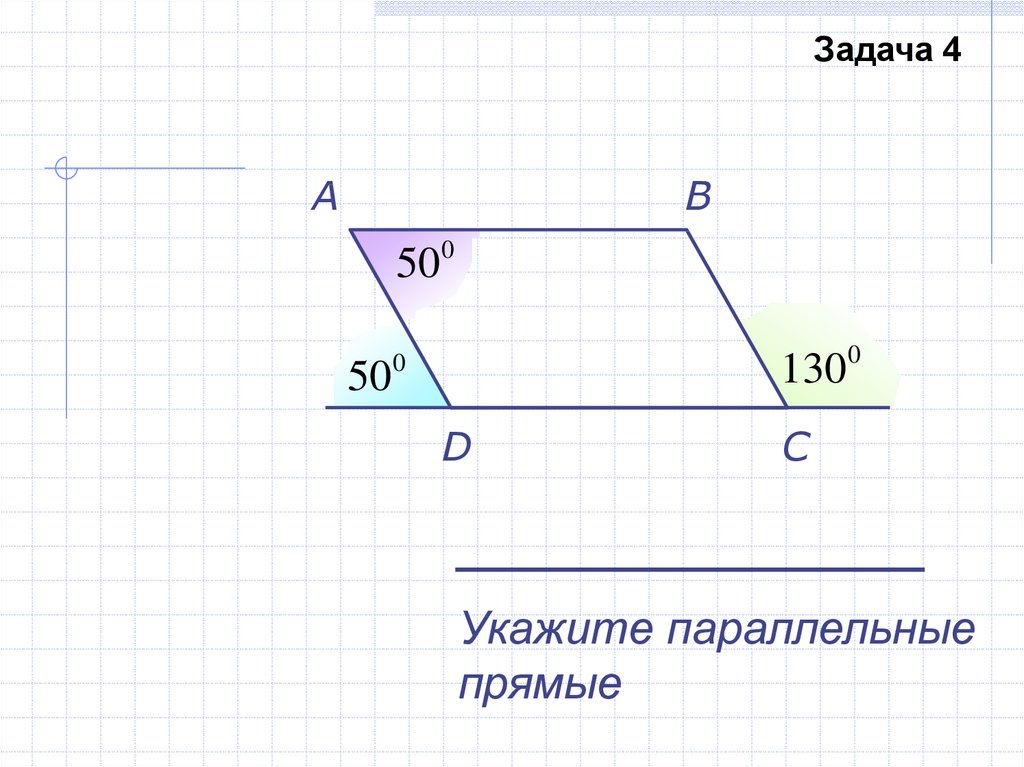
38.
Задача 4A
B
500
50
130
0
D
0
C
Укажите параллельные
прямые
39.
Свойства параллельных прямыхЕсли две параллельные прямые пересечены секущей, то накрест лежащие
углы равны.
c
а
1
2
b
c
Если две параллельные прямые пересечены секущей, то соответственные
углы равны.
Если две параллельные прямые пере- сечены
секущей, то сумма односторон- них углов
равна 1800.
1
а
2
b
c
а
1
2
b
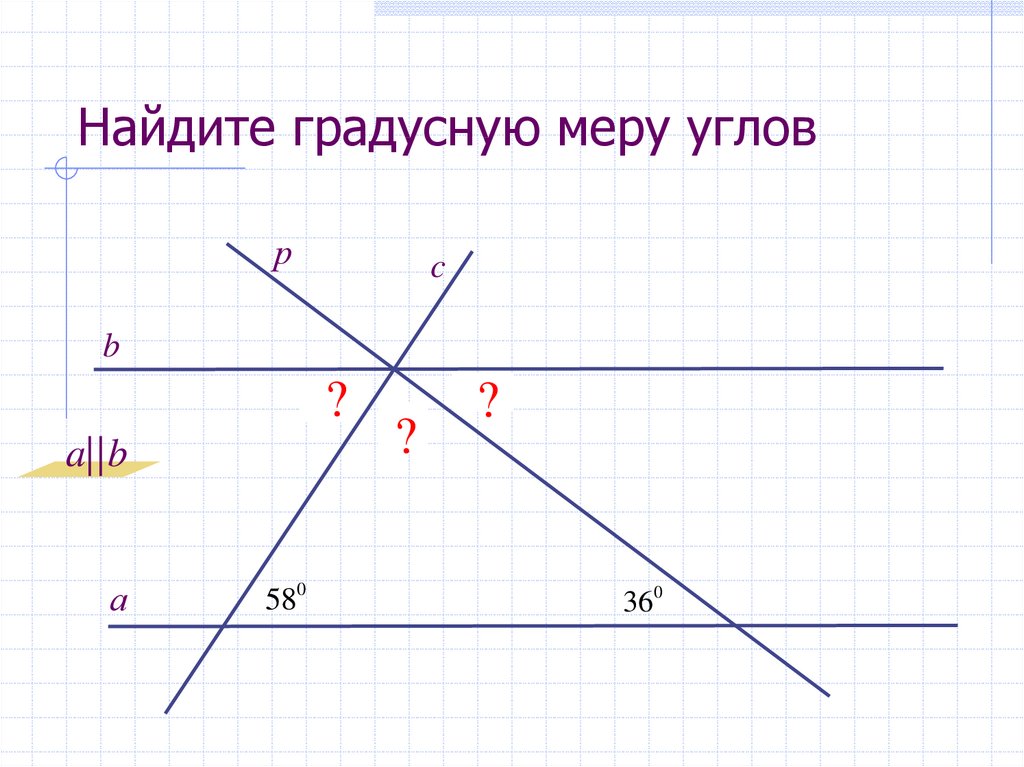
40. Найдите градусную меру углов
рc
b
?
580
a||b
а
580
860
?
360
?
360
41. Найдите градусную меру углов
c?45
0
b
?
750
a||b
а
0
45
р
750
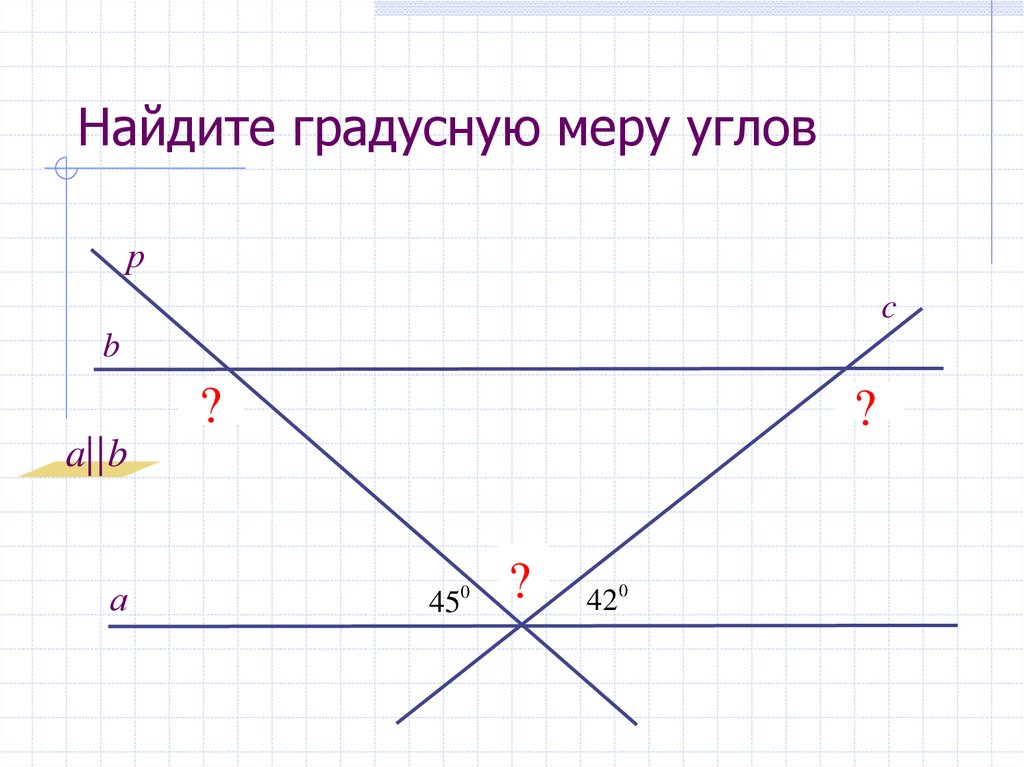
42. Найдите градусную меру углов
рc
b
1350
1380
?
?
a||b
а
450
930
?
420
43. Найдите градусную меру углов
b230
210
a||b
?
а
230
c
?
1360
р
?
440
44.
На рисунке АС II ВD иНайдите СВD.
A
АС = АВ,
МАС = 400.
M
С
400
2
3
B
1
D
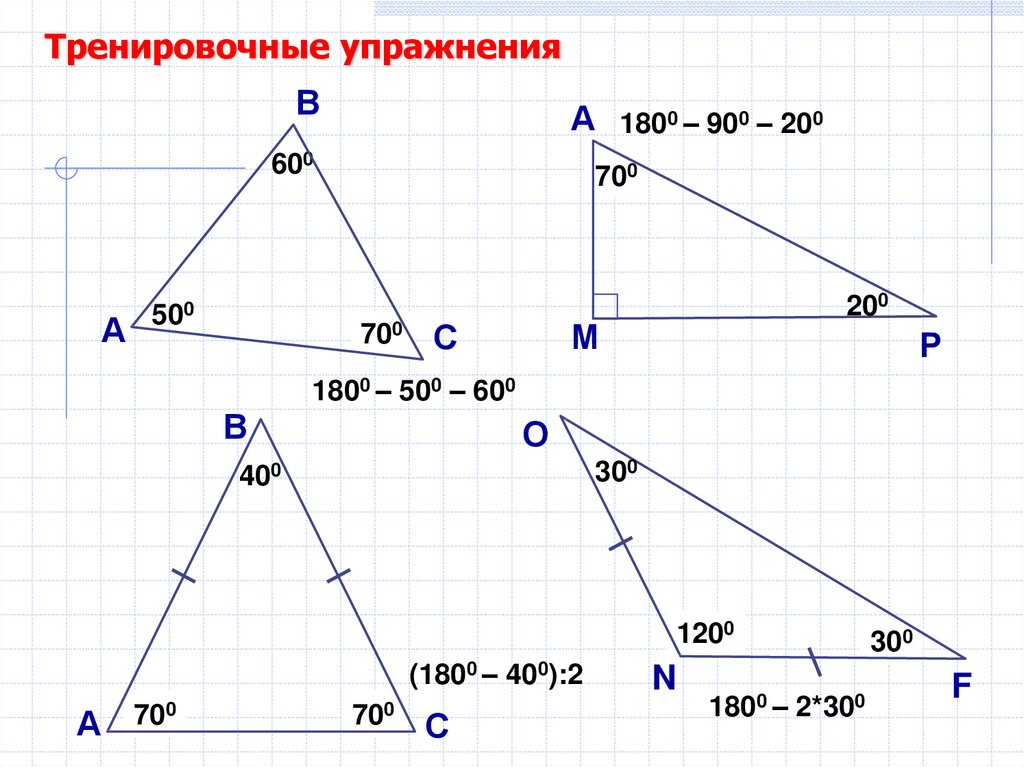
45.
Тренировочные упражненияВ
А 1800 – 900 – 200
?
700
600
А
500
70
?0
200
М
С
Р
1800 – 500 – 600
В
О
300
400
120
? 0
(1800 – 400):2
А ?
700
?
700
С
N
1800 – 2*300
30?0
F
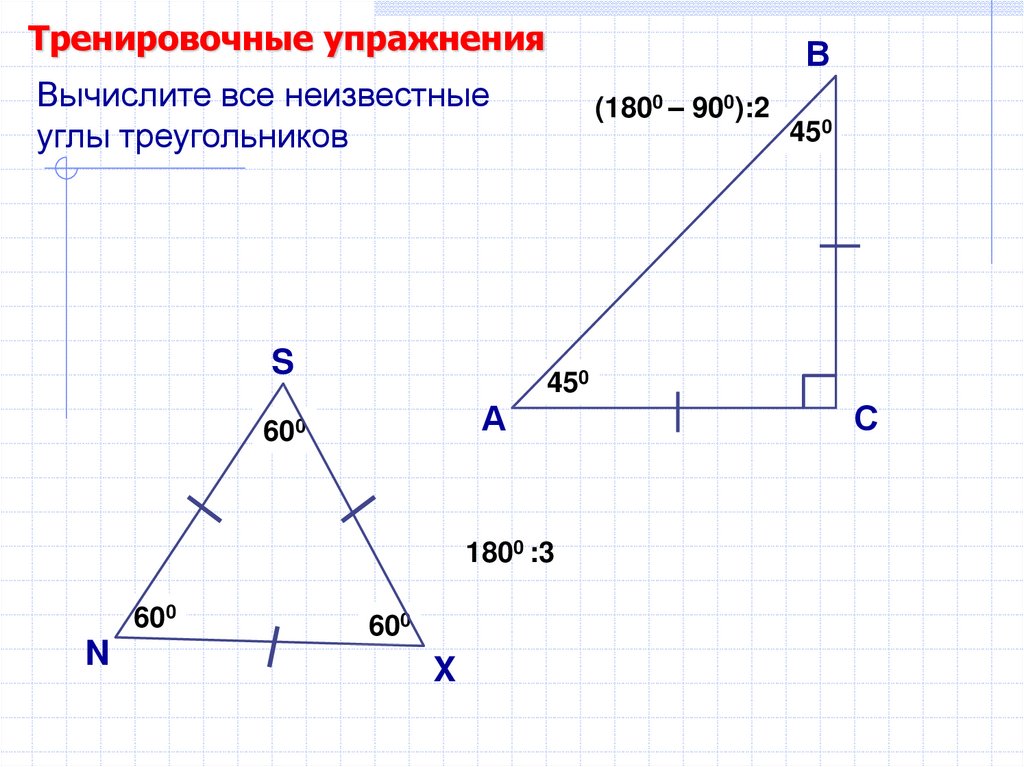
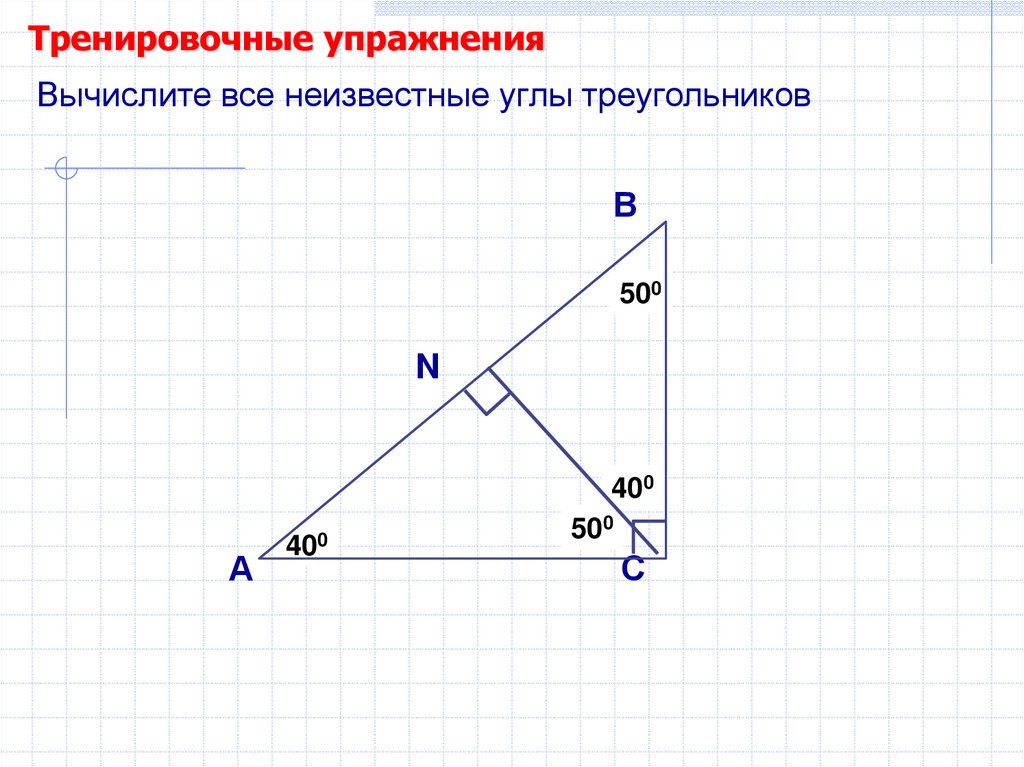
46.
Тренировочные упражненияВ
Вычислите все неизвестные
углы треугольников
S
А
600
(1800 – 900):2
45
?0
1800 :3
600
N
600
X
?0
45
С
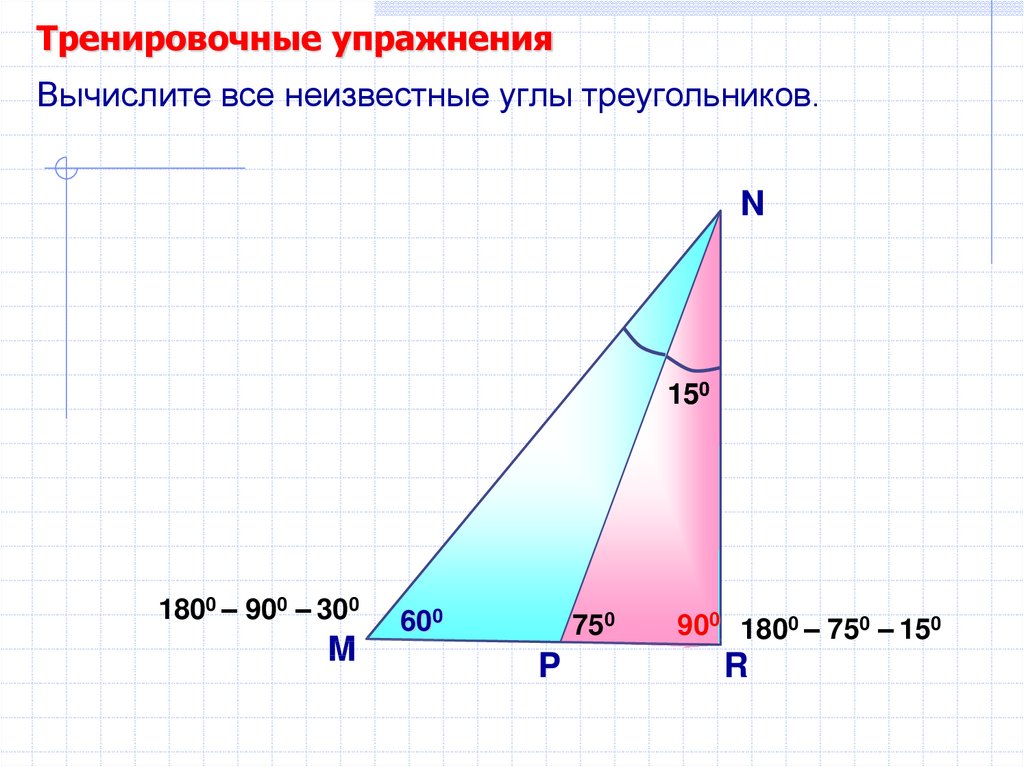
47.
Тренировочные упражненияВычислите все неизвестные углы треугольников.
N
150
1800 – 900 – 300
M
600
750
P
900 1800 – 750 – 150
R
48.
Тренировочные упражненияВычислите все неизвестные углы треугольников
В
?0
50
N
?0
40
А
?0
40
50
?0
С
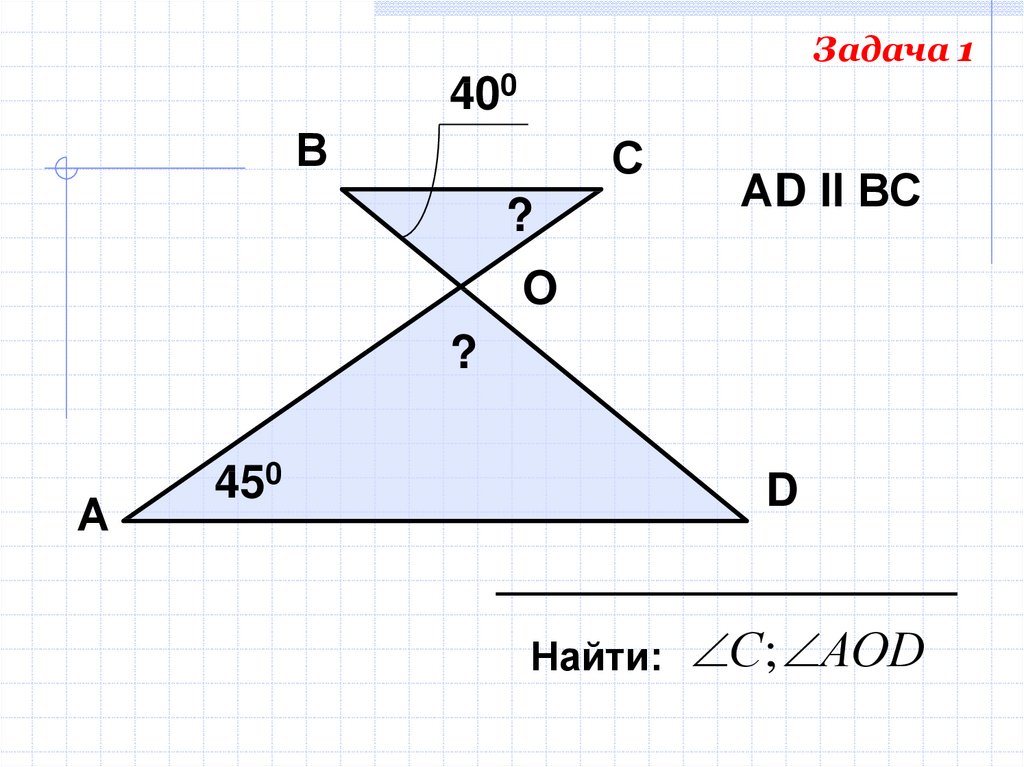
49.
Задача 1400
В
С
?
АD ll ВС
O
?
А
450
D
Найти:
С; АОD
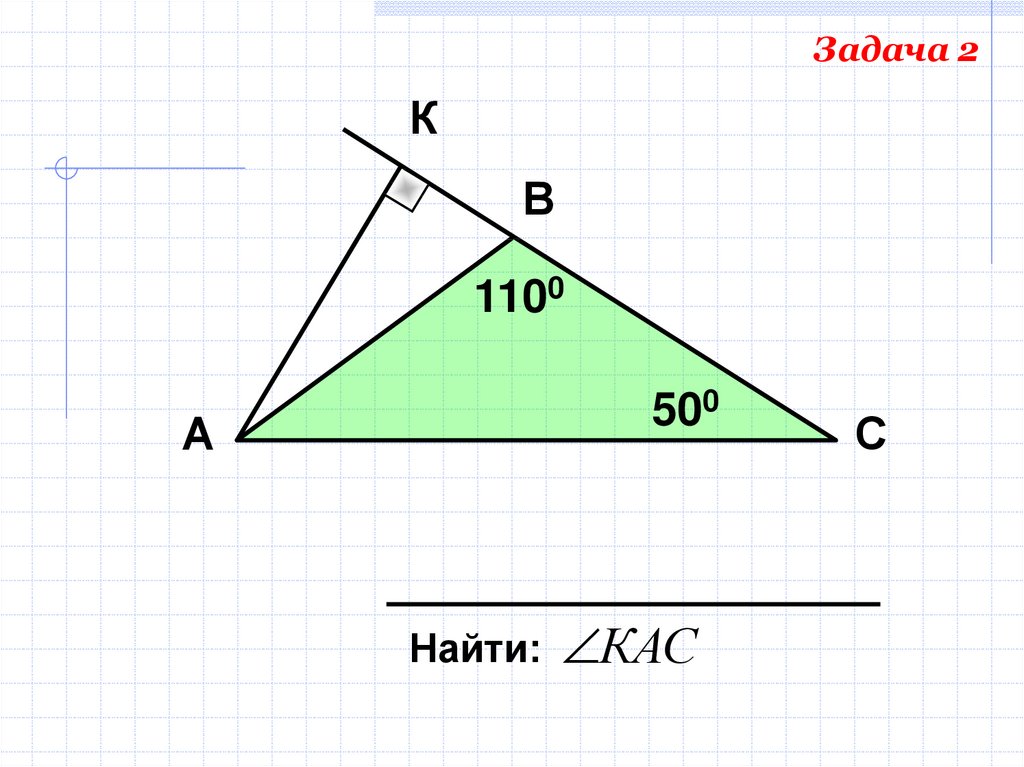
50.
Задача 2К
В
1100
500
А
Найти:
КАС
С
51.
Задача 3В
480
?
D
560
А
Найти:
С
DВЕ; D
Е
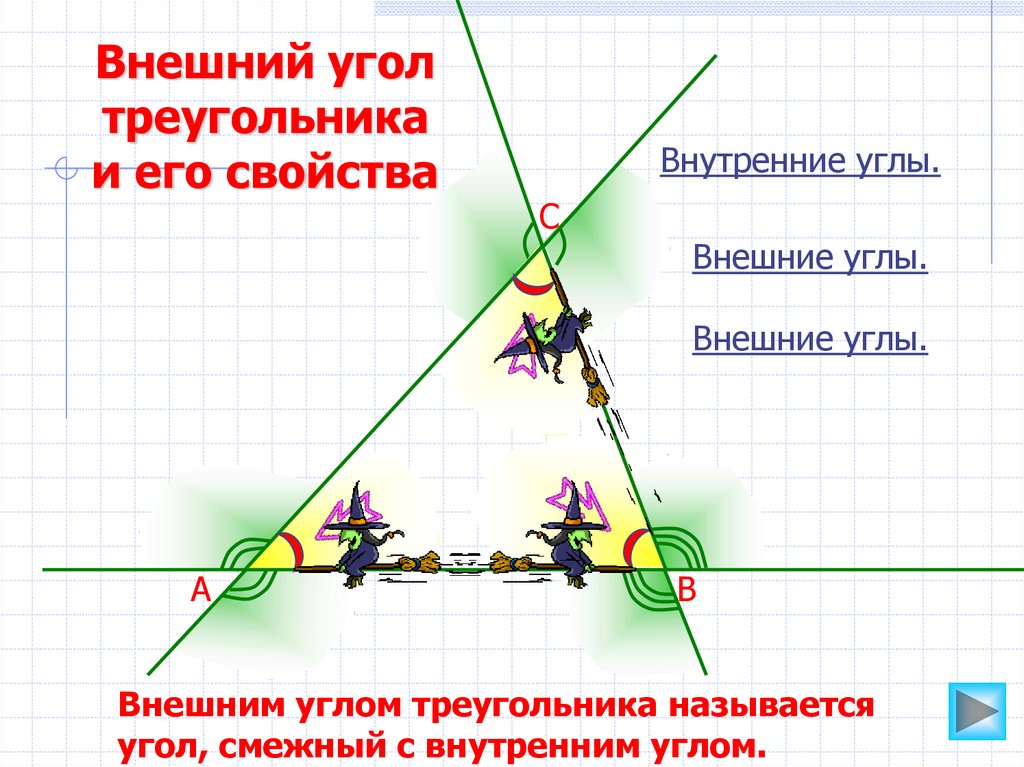
52.
Внешний уголтреугольника
и его свойства
Внутренние углы.
С
Внешние углы.
Внешние углы.
А
В
Внешним углом треугольника называется
угол, смежный с внутренним углом.
53.
Внешний угол треугольника равен суммедвух внутренних углов, не смежных с ним.
С
4 = 1 + 2
2
А
1
3
4
В
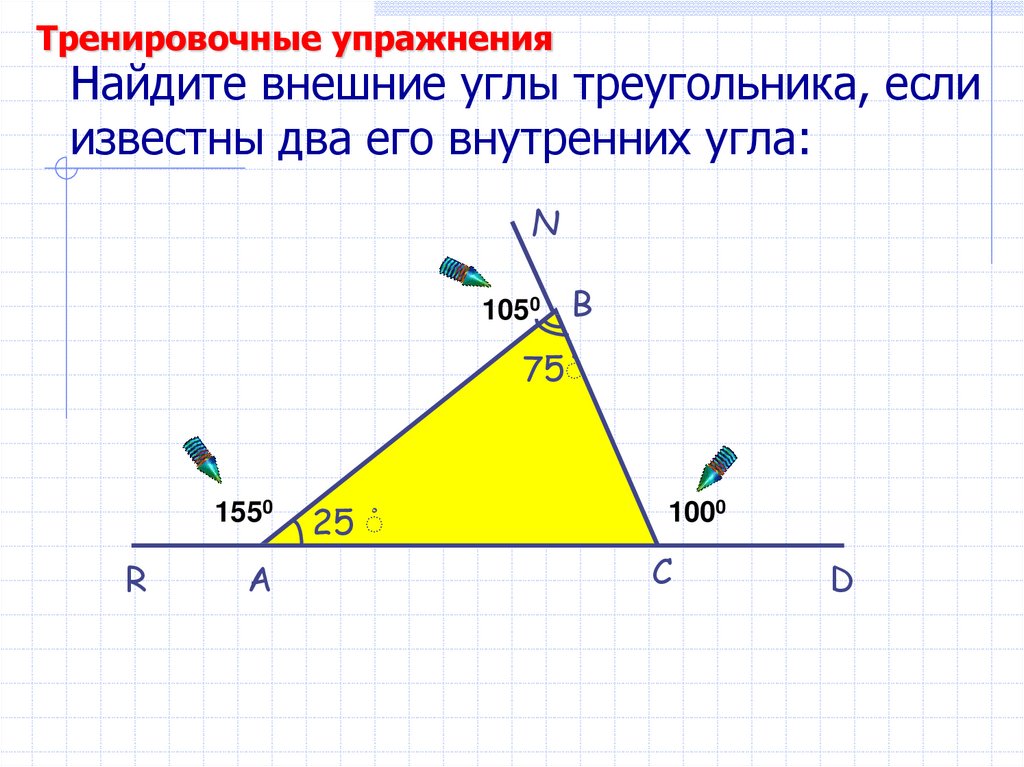
54. Найдите внешние углы треугольника, если известны два его внутренних угла:
Тренировочные упражненияНайдите внешние углы треугольника, если
известны два его внутренних угла:
N
1050
В
75ْ
1550
R
А
25 ْ
1000
С
D
55. Найдите углы треугольника, если известны два его внешних угла:
Тренировочные упражненияНайдите углы треугольника, если известны
два его внешних угла:
В
М
80ْ
1000
150ْ
К
А
300
500
С
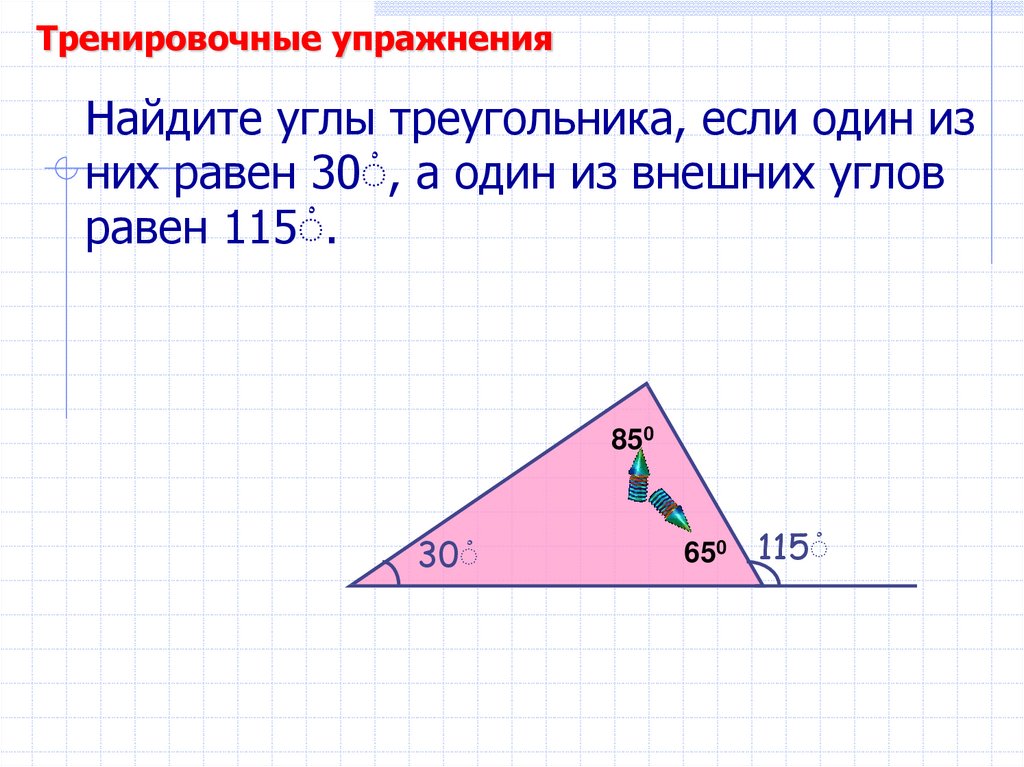
56. Найдите углы треугольника, если один из них равен 30ْ, а один из внешних углов равен 115ْ.
Тренировочные упражненияНайдите углы треугольника, если один из
них равен 30ْ, а один из внешних углов
равен 115ْ.
850
30ْ
650
115ْ
57.
Рассказать о соотношении междусторонами и углами треугольника.
В
В треугольнике:
против большей стороны
лежит больший угол;
обратно,
С
А
против большего угла
лежит большая сторона.
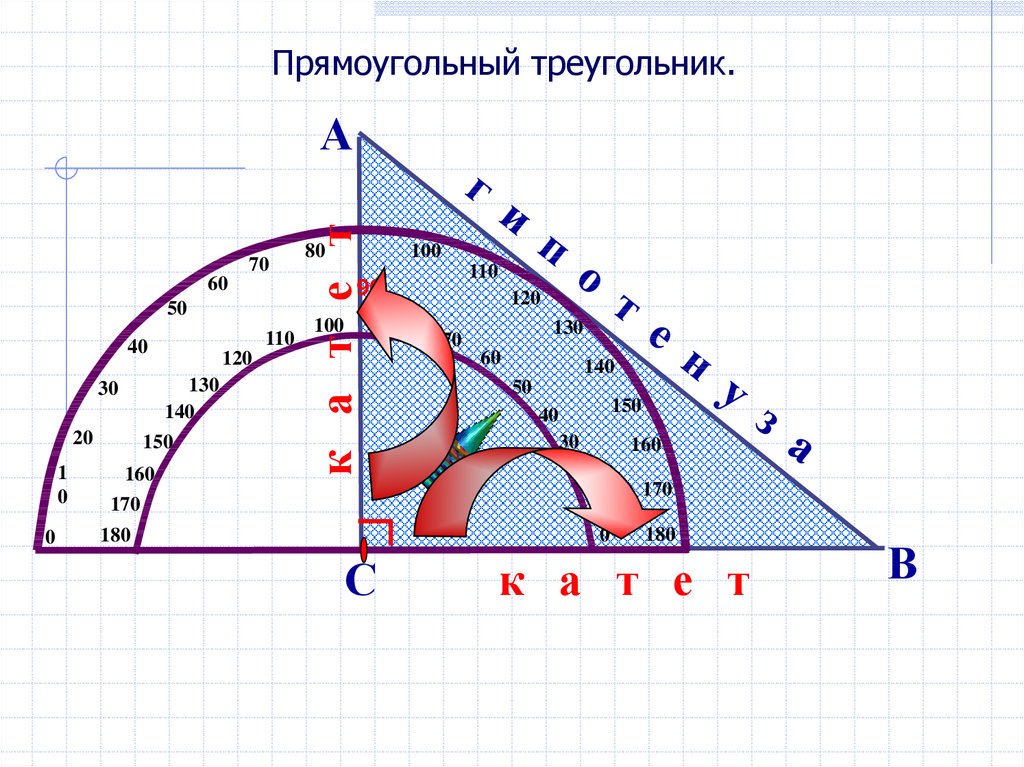
58.
Прямоугольный треугольник.70
60
50
40
130
140
150
30
20
1
0
0
160
110
120
к а т е т
А
80
100
110
90
100
170
120
80
70
130
60
140
50
150
40
30
20
160
10
180
0
С
170
180
к а т е т
В
59.
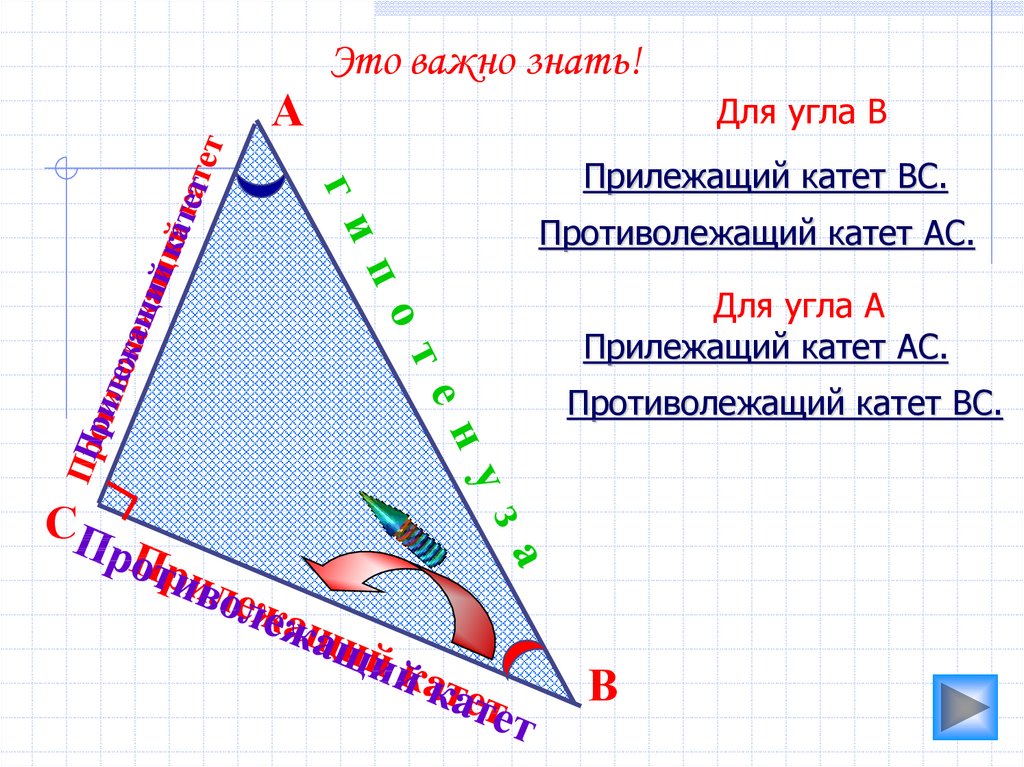
АЭто важно знать!
Для угла В
Прилежащий катет ВС.
Противолежащий катет АС.
Для угла А
Прилежащий катет АС.
Противолежащий катет ВС.
С
В
60.
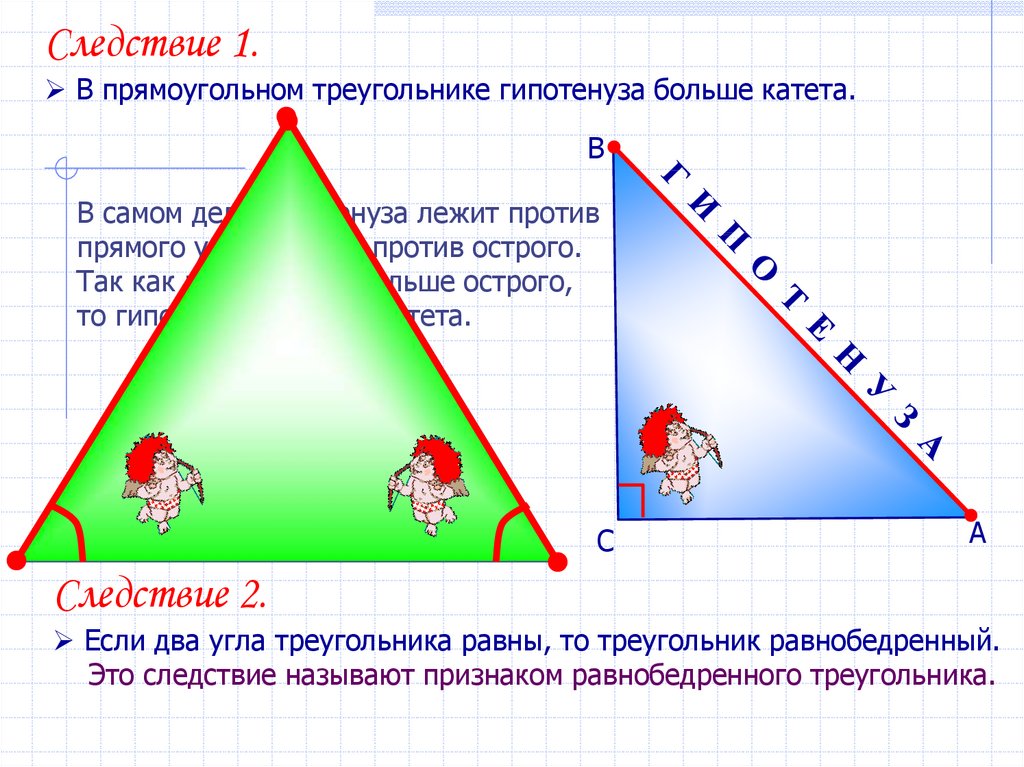
Следствие 1.В прямоугольном треугольнике гипотенуза больше катета.
В
В самом деле гипотенуза лежит против
прямого угла, а катет против острого.
Так как прямой угол больше острого,
то гипотенуза больше катета.
С
А
Следствие 2.
Если два угла треугольника равны, то треугольник равнобедренный.
Это следствие называют признаком равнобедренного треугольника.
61.
Почему не существует треугольника со сторонами14, 6 и 7.
Неравенство треугольника.
6
7
14
14<6+7
62.
Неравенство треугольника.Каждая сторона треугольника меньше суммы двух других
сторон.
АВ < ВС + АС
В
ВС < АВ + АС
АС < АВ + ВС
А
С
Достаточно проверять
выполнение неравенства
для большей стороны.
63.
Неравенство треугольника.Каждая сторона треугольника меньше суммы двух других сторон.
Найди треугольники, которые не существуют и щелкни по ним мышкой.
В
R
6
12
С
Достаточно проверить
выполнение неравенства
для большей стороны.
18
14
14<6+7
18<12+8 (Верно)
N
8
А
В
7
Q
11
4
С
8
9
11<4+7
7
N
14<9+8 (Верно)
14
64.
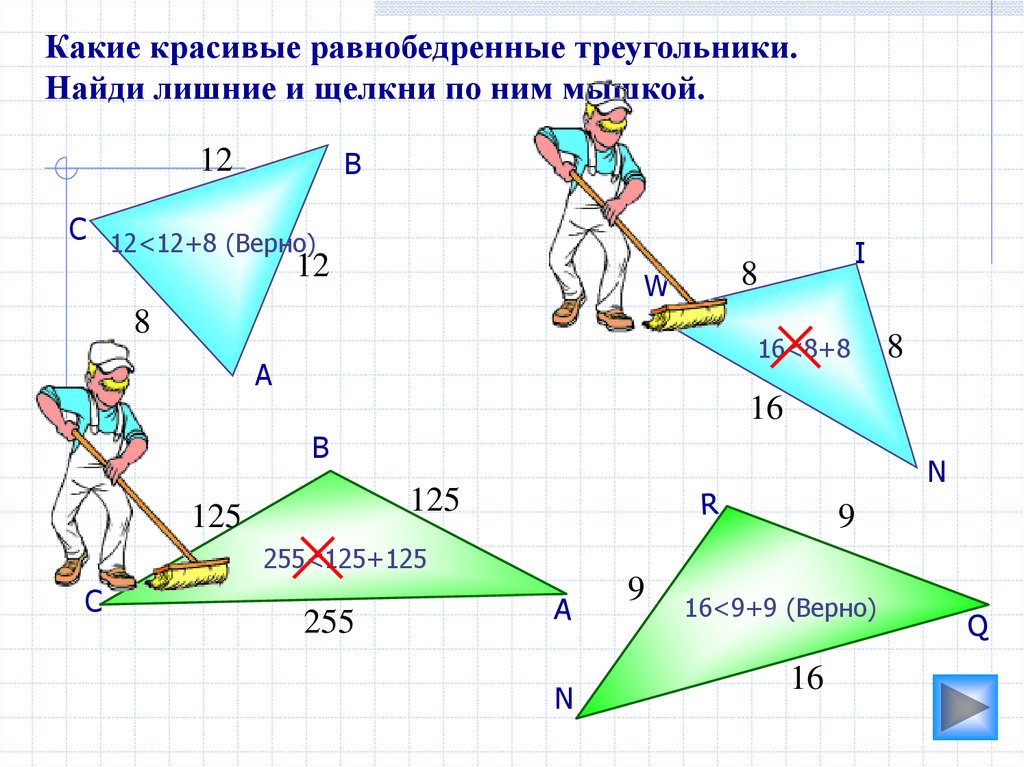
Какие красивые равнобедренные треугольники.Найди лишние и щелкни по ним мышкой.
В
12
С 12<12+8 (Верно)
12
W
8
I
8
16<8+8
А
8
16
В
N
125
125
9
255<125+125
С
9
255
N
16<9+9 (Верно)
16
65.
У треугольника не хватает одной стороны.Какое из предложенных чисел подойдет?
Щелкни по нему мышкой.
R
3
8
А
8<6+3
В
5
8<5+3
12
12<8+3
3
8<3+3
11
11<8+3
6
Чтобы раскрыть проверку, щелкните на число второй раз
66.
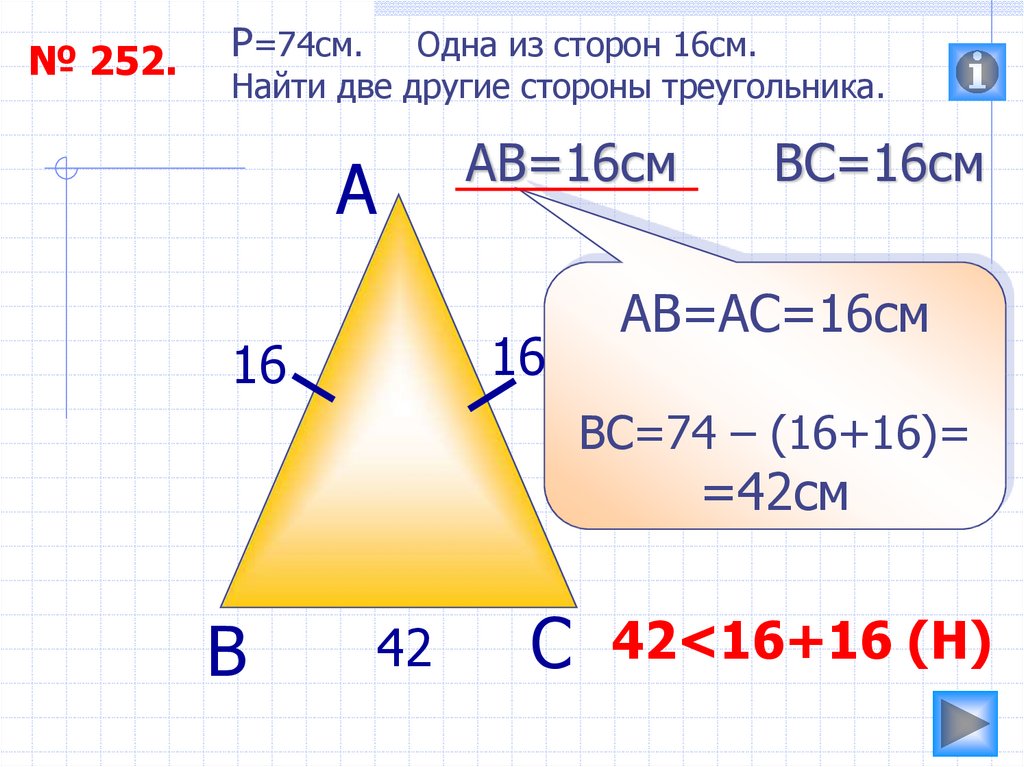
№ 252.P=74см.
Одна из сторон 16см.
Найти две другие стороны треугольника.
А
АВ=16см
16
16
ВС=16см
АВ=АС=16см
ВС=74 – (16+16)=
=42см
В
42
С
42<16+16 (Н)
67.
№ 252.P=74см.
Одна из сторон 16см.
Найти две другие стороны треугольника.
А
АВ=16см
АВ=(74 –16):2=
29
29
ВС=16см
=29см
29<29+16 (В)
В
16
С
Ответ: стороны треугольника 29, 29, 16см.
68.
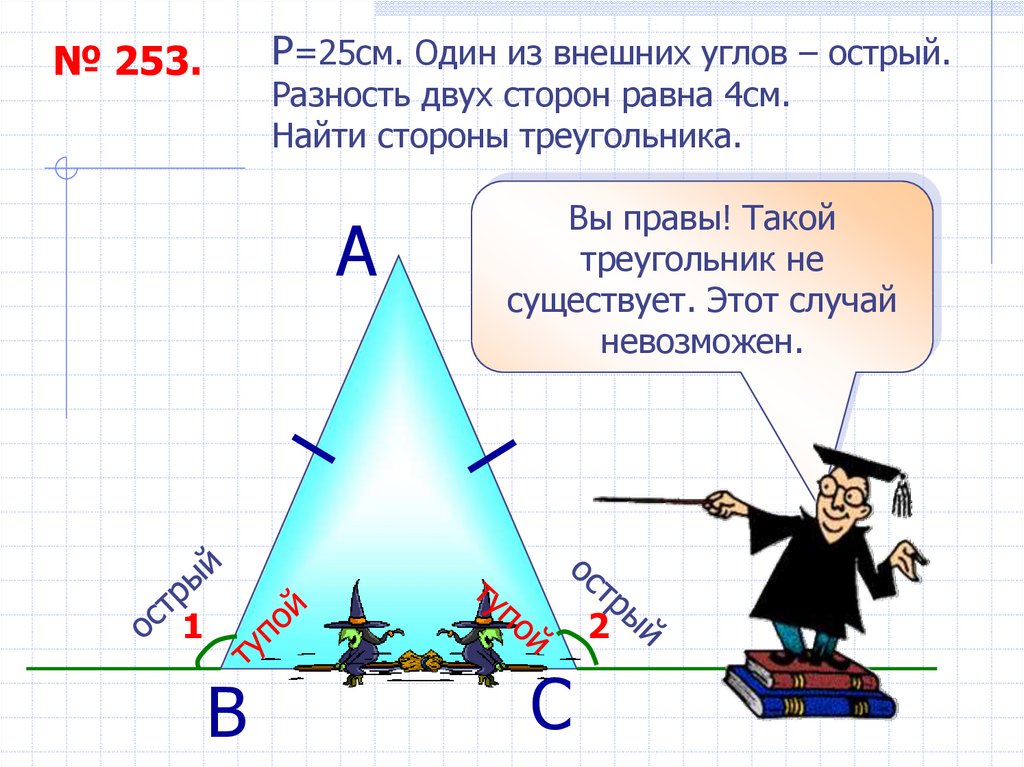
P=25см. Один из внешних углов – острый.№ 253.
Разность двух сторон равна 4см.
Найти стороны треугольника.
А
Вы правы! Такой
треугольник не
существует. Этот случай
невозможен.
1
2
В
С
69.
P=25см. Один из внешних углов – острый.№ 253.
Разность двух сторон равна 4см.
Найти стороны треугольника.
х
В
А
тупой
острый
х
большая
х+4сторона
С
70.
Это важно знать.М
Для угла Р
Прилежащий катет РТ.
Противолежащий катет МТ.
Для угла М
Прилежащий катет МТ.
Противолежащий катет РТ.
Т
Р
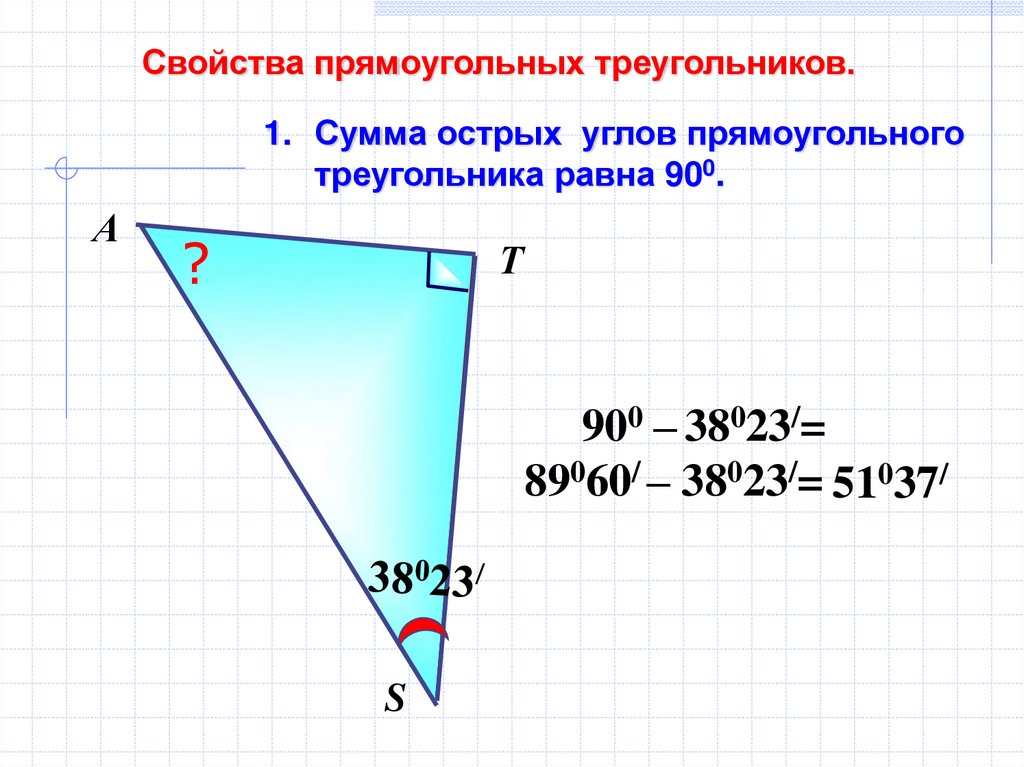
71.
Свойства прямоугольных треугольников.1. Сумма острых углов прямоугольного
треугольника равна 900.
А
?
Т
900 – 38023/=
89060/ – 38023/= 51037/
S
72.
2. Катет прямоугольного треугольника, лежащийпротив угла в 300, равен половине гипотенузы.
С
2,1см
300
А
4,2см
В
73.
3. Если катет прямоугольного треугольника равенполовине гипотенузы, то угол, лежащий против
этого катета, равен 300.
С
300
А
5,24см
В
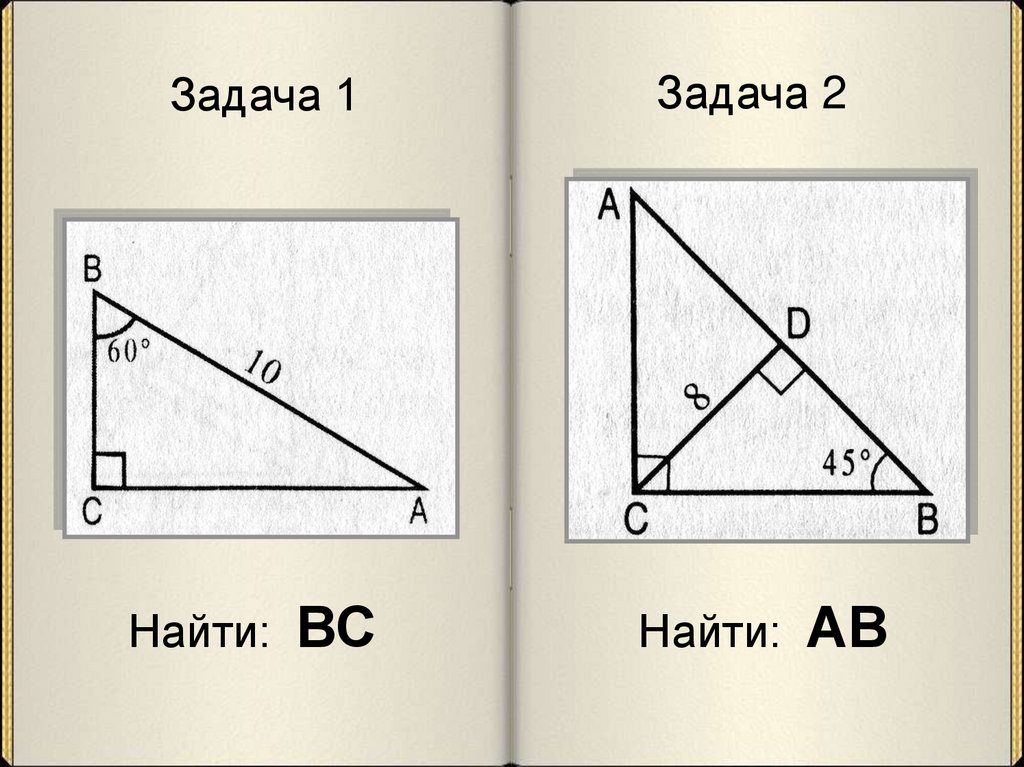
74. Задача 1
Найти:ВС
Задача 2
Найти:
АВ
75. Задача 3
Найти:АЕ
Задача 4
Найти:
угол В
угол А
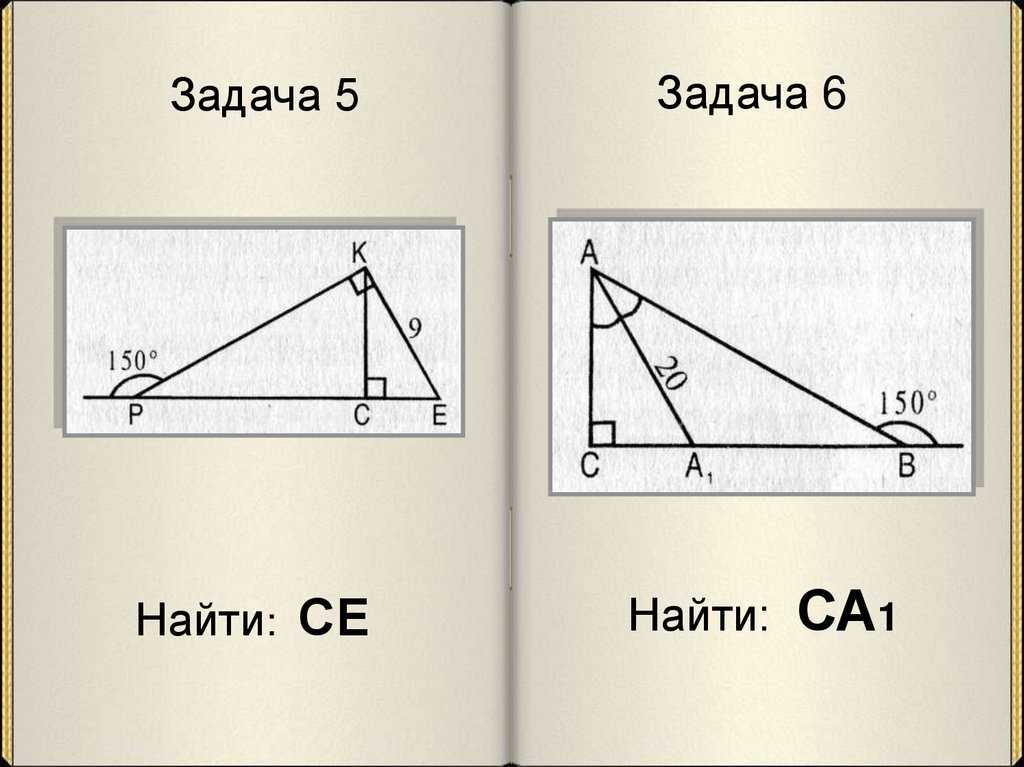
76. Задача 5
Найти: СЕЗадача 6
Найти:
СА1
77. Задача 7
Найти:угол САD
Задача 8
Найти:
АD






































 Математика
Математика








