Похожие презентации:
Оптика. Уравнения Максвелла. (Лекция 1)
1. ОПТИКА
Скиданов Р.В.2. Введение
Световым полем называют электромагнитное поле в оптическом диапазоне частот.Оптические частоты чрезвычайно велики (порядка 1014-1015), а разность частот между
границами оптического диапазона очень мала по сравнению с их величинами, поэтому
принято измерять оптический диапазон в длинах волн.
1. В оптическом диапазоне выполняются законы геометрической оптики,
2. В оптическом диапазоне свет очень слабо взаимодействует с веществом.
Оптический диапазон состоит из следующих видов излучения:
рентгеновское,
ультрафиолетовое (УФ),
видимое,
инфракрасное (ИК).
Если во времена Ньютона в оптический диапазон входило только видимое излучение, то с
техническим прогрессом диапазон существенно расширился, причем рентгеновское
излучение включено в оптический диапазон совсем недавно – примерно 20 лет назад.
3. Уравнения Максвелла
Уравнения Максвелла явились итогом интенсивных исследований электричества, магнетизма исветовых явлений, проводимых в первой половине XIX века. В то время, когда стало ясно, что
свет и электромагнитное поле – это одно и то же, появился и универсальный математический
аппарат, связывающий между собой функции изменения во времени и пространстве
электрического и магнитного полей. Электромагнитное поле по своей природе векторное, то
есть все его изменения, происходящие во времени, имеют определенную ориентацию в
пространстве. Основными величинами, определяющими электромагнитное поле, являются
вектор электрической напряженности поля и вектор магнитной напряженности поля .
Эти векторы являются функциями времени и координат в пространстве, описываемых радиусвектором :
E E r, t , E вольт / м
H H r, t , H А / м
вектор электрической напряженности поля
вектор магнитной напряженности поля
D D r, t , D кл / м 2
вектор электрической индукции
B B r, t , B вебер / м 2
вектор магнитной индукции
r, t , кл / м 3
объемная плотность заряда
J J r, t , J А / м 2
поверхностная плотность тока
r , r
электрическая и магнитная проницаемость
4. Уравнения Максвелла
E BH D J уравнения Максвелла
D
B 0
D E
B H
B
t
D
rotH
J
t
divD
rotE
уравнения Максвелла
в классических обозначениях
divB 0
материальные уравнения
E B
H D уравнения Максвелла в вакууме
D 0
B 0
Для вакуума из уравнений Максвелла можно получить следующее важное соотношение:
1 с –скорость света в вакууме, ε0 и μ0 - электрическая и магнитная
0 0
с постоянные в вакууме
5. Уравнения Максвелла
Электрическая проницаемость для разных сред может принимать различные значения,а магнитная проницаемость для оптических частот во всех средах практически не
отличается отμ0. Для линейных сред ε и μ не зависят от E и H, то есть электрическая и
магнитная постоянные линейной среды не зависят от интенсивности света.
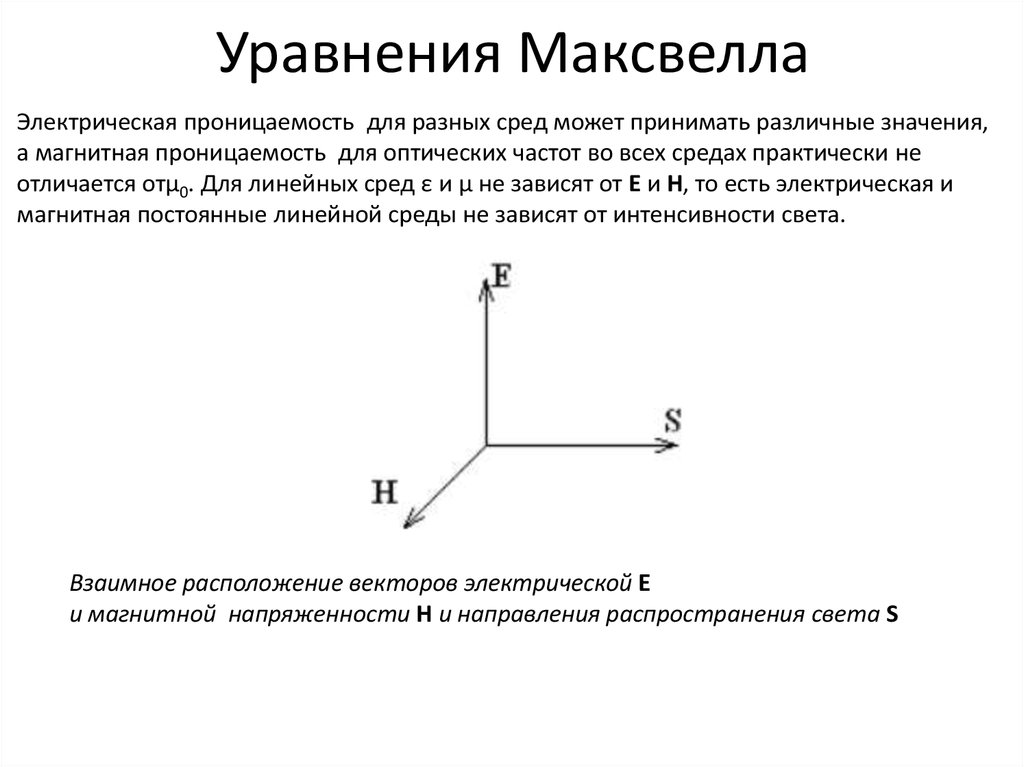
Взаимное расположение векторов электрической E
и магнитной напряженности H и направления распространения света S
6. Математическое описание электромагнитных волн
E BB
H
t
t
2
D
2E
H
2 E 2
E
H
t
t
t
t t
t
2E
E E 2
t
2
2E
E 2 0
t
2 Ex
2
E x
t 2
2
Ey
2
E y
t 2
2 Ez
2
E z 2
t
2
D 0
2H
H 2
t
2
2H x
H x
t 2
2H y
2
H y
t 2
2H z
2
H z
t 2
2
2E
E 2
t
2





 Физика
Физика








