Похожие презентации:
Теорема о циркуляции вектора магнитной индукции. (Лекция 14)
1.
Теорема о циркуляции вектора магнитной индукции:Циркуляция вектора магнитной индукции
по произвольному замкнутому
контуру равна алгебраической сумме
токов, охватываемых этим контуром,
умноженной на магнитную постоянную
B
d
l
=
m
I
0
i
l
где
i
-7
m 0 = 4p ×10Гн
м
2.
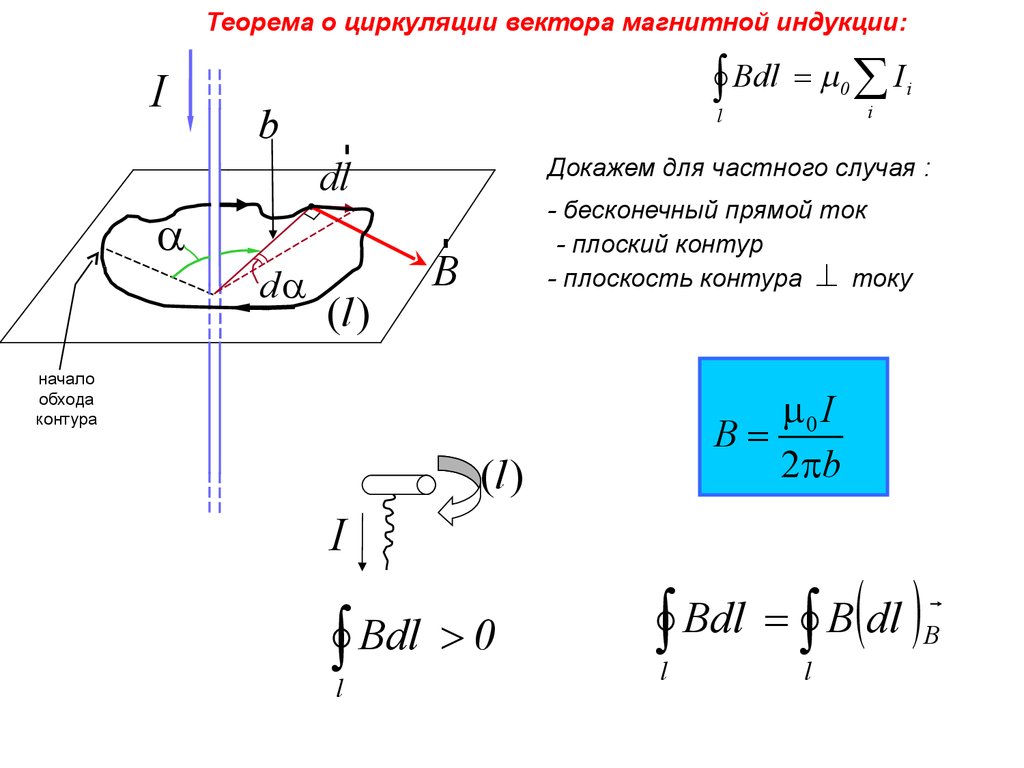
Теорема о циркуляции вектора магнитной индукции:I
b
Bdl = m0 I i
r
dl
a
da
(l )
Докажем для частного случая :
- бесконечный прямой ток
- плоский контур
- плоскость контура току
r
B
начало
обхода
контура
m0 I
B=
2pb
(l )
I
Bdl 0
l
i
l
B
d
l
=
B
d
l
B
l
l
3.
aI
r
dl
b
da
r
dl
r
B
r
dl
r
B
= b × da
r
B
2p m 0 I
m 0 I 2p
l Bdl = 0 2pb bda = 2p 0 da =m0 I
B
d
l
=
m
I
0
l
4.
1(l )
I
a
Если контур не охватывает ток….
m0 I
l Bdl = 2p
2p
m0 I 2
m0 I 1
0 da = 2p 1 da 2p 2 da =0
2
Если контур произвольной формы….
r
r
dl dl
r
dlP
dl = dl dl II
Bdl = Bdl BdlII =0 BdlII
l
r
B
l
l
B
d
l
=
m
I
0
l
l
5.
В общем случае для системы токов произвольной формы ипроизвольного замкнутого контура:
B
d
l
=
m
I
0
i
l
I2
I1
I3 I 4
i
I1 = 1A
I2 = 2 A
I3 = 3 A
I4 = 4 A
r r
Ñ
Bd l = m0 (I1 I2 I3 I4 ) = m0 (0 - 2 3 - 4)
l
6.
В общем случае, для контура в среде, гдесуществует постоянный ток….
I = jn dS
S
Bdl =mm0 jn dS
l
S
7.
Магнитное поле внутри прямого проводника с токомI
r
r
R
Симметрия: в равноотстоящих
от оси точках поле одинаково.
(l )
Bdl = Bl dl = Bdl =B dl =B 2pr
l
l
l
l
8.
Ir
r
Магнитное поле прямого проводника с током
Симметрия: в равноотстоящих
от оси точках поле одинаково.
Bdl = Bl dl = Bdl =B dl =B 2pr
R
l
l
l
l
Полый проводник
(l )
Bdl =B 2pr
r R
l
Bdl =m0 I
m0 I
B=
2pr
l
r<R
Bdl =B 2pr
l
Bdl =0
l
B=0
9.
Равномерное распределение тока по сечению сплошного проводникаBdl =B 2pr
l
Bdl =m0 I ¢
r<R
l
Sl = pr I ¢ =
2
Sl
I
2
jn dS = jSl =
p
r
2
pR
B
0
B
R
r
0
m0 I
B=
r
2
2pR
Полый проводник
R
r
10.
Магнитное поле бесконечно длинного соленоидаСоленоид -…….
I
D
1)
Рассмотрим….АА…
A
r
dl1
r
dB
r
dB2
r
dB1
r
r1
r
dl2
r
r2
A
r
r
Idl1 = Idl2
r
r
dB1 = dB2
r
r
r
dB = dB1 dB2
r r
Все dB и B Pоси соленоида
11.
rIdl1
2)
r1 , r2 D
D
r
Idl2
r
r1
r
dB2
r
r2
r
r
Idl1 = Idl2
r
r
dB1 = dB2
r
r
r
dB = dB1 dB2 = 0
r
dB1
r1 » r2 D
r
B=0
12.
(l )1® 2 ® 3 ® 4 ®1
I
2
1
2
3
4
1
Bdl = Bl dl = Bl dl Bl dl Bl dl Bl dl
l
l
l
4
1
2
3
4
2
Bdl = Bl dl 0 0 0 = - B l
3
l
1
по т. о циркуляции Bdl = 0
l
вне соленоида B = 0
13.
(l )I
2
1
1® 2 ® 3 ® 4 ®1
2
3
4
1
Bdl = Bl dl = Bl dl Bl dl Bl dl Bl dl
l
l
1
2
3
4
l
4
3
2
Bdl = Bl dl 0 0 0 = - B l
l
1
по т. о циркуляции Bdl = m 0 N I = m 0 n l I
l
N - ....n - ....
в соленоиде B = m 0 × n × I
14.
магнитное поле внутри бесконечно длинного соленоида однородномагнитное поле вне бесконечно длинного соленоида отсутствует
Реальное поле соленоида :













 Физика
Физика








