Магнитное поле. Лекция 19. Закон Био-Савара-Лапласа. Теорема о циркуляции вектора магнитной индукции

1.

МАГНИТНОЕ ПОЛЕ
Лекция 19.
Тема: Закон Био-Савара-Лапласа.
Теорема о циркуляции
вектора магнитной индукции.
Учебник:
Трофимова Т.И. Курс физики : учеб. пособ. для вузов / Т. И.
Трофимова. - М.: Академия, 2007.- с. 202-206, с. 214-217.
к.ф.-м.н.
Курочкин А.Р.

2.

Электрическое поле – одна из сторон электромагнитного поля,
создаваемая
• электрическими зарядами и
• изменяющимся магнитным полем и передающая действие
электрических сил.
1. Электростатика изучает взаимодействие неподвижных
зарядов и свойства постоянного электрического поля.
2. Электродинамика – рассматривает явления и процессы,
обусловленные движением электрических зарядов.
2

3.

Опыт Эрстеда
Эрстед
Ханс Кристиан
1777 - 1851
• Эрстед помещал над магнитной стрелкой прямолинейный
металлический проводник, направленный параллельно стрелке.
• При пропускании через проводник электрического тока магнитная
стрелка поворачивалась почти перпендикулярно проводнику.
• При изменении направления тока стрелка разворачивалась на 180°.
• Аналогичный разворот наблюдался, если провод переносился на
3
другую сторону, располагаясь не над, а под стрелкой.

4.

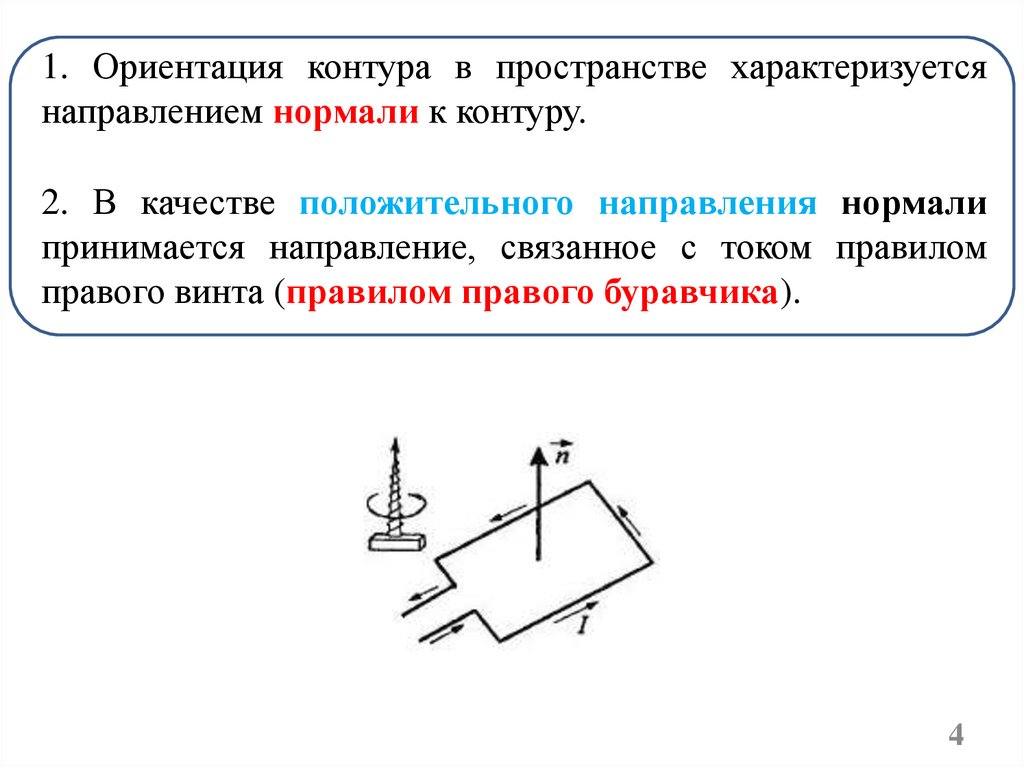
1. Ориентация контура в пространстве характеризуется
направлением нормали к контуру.
2. В качестве положительного направления нормали
принимается направление, связанное с током правилом
правого винта (правилом правого буравчика).
4

5.

3. Магнитное поле оказывает на рамку с током
ориентирующее действие, поворачивая её определённым
образом.
4. За направление магнитного поля в данной точке
принимается направление:
а. вдоль которого располагается положительная нормаль
к свободно подвешенной рамке с током,
б. направление, совпадающее с направлением силы,
действующей на северный полюс магнитной стрелки,
помещенный в данную точку поля.
S
N
n
I
5

6.

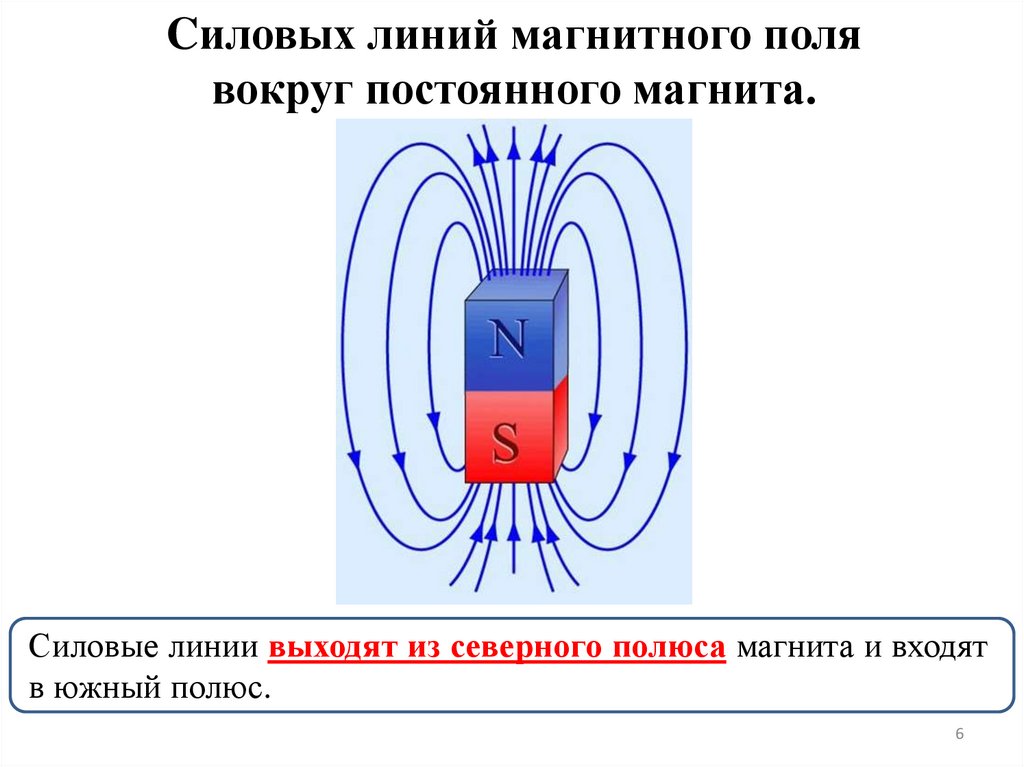
Cиловых линий магнитного поля
вокруг постоянного магнита.
Силовые линии выходят из северного полюса магнита и входят
в южный полюс.
6

7.

7

8.

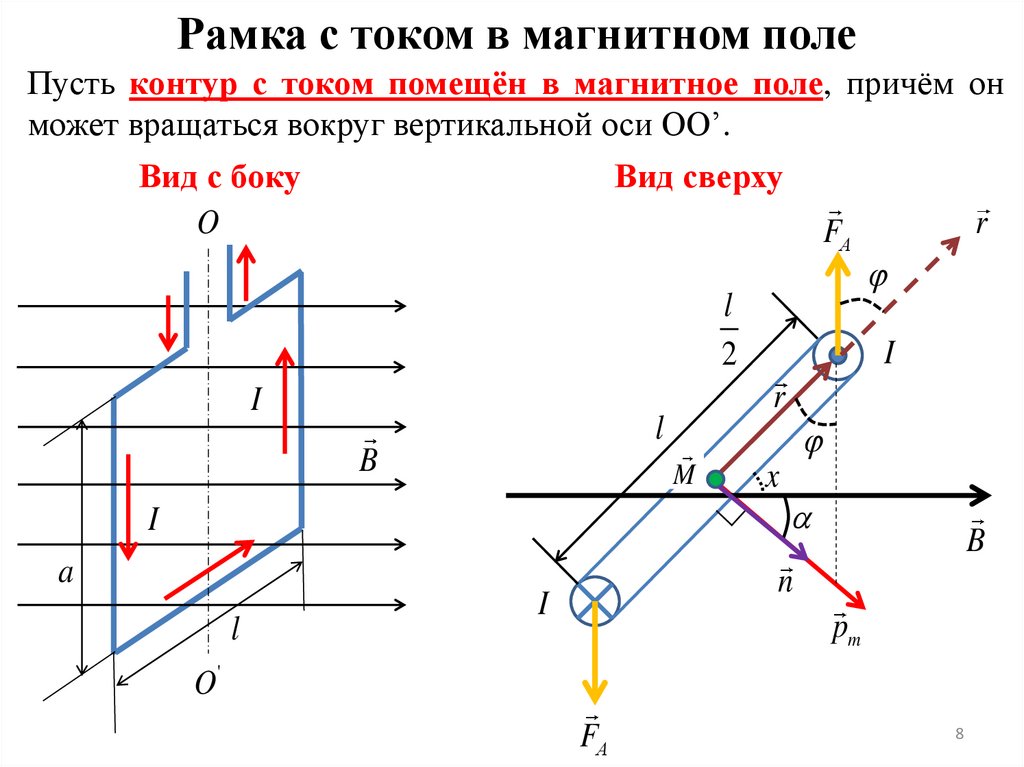
Рамка с током в магнитном поле
Пусть контур с током помещён в магнитное поле, причём он
может вращаться вокруг вертикальной оси OO’.
Вид сверху
Вид с боку
O
FА
l
2
I
r
I
l
B
M
I
a
l
r
x
B
n
I
pm
O'
FА
8

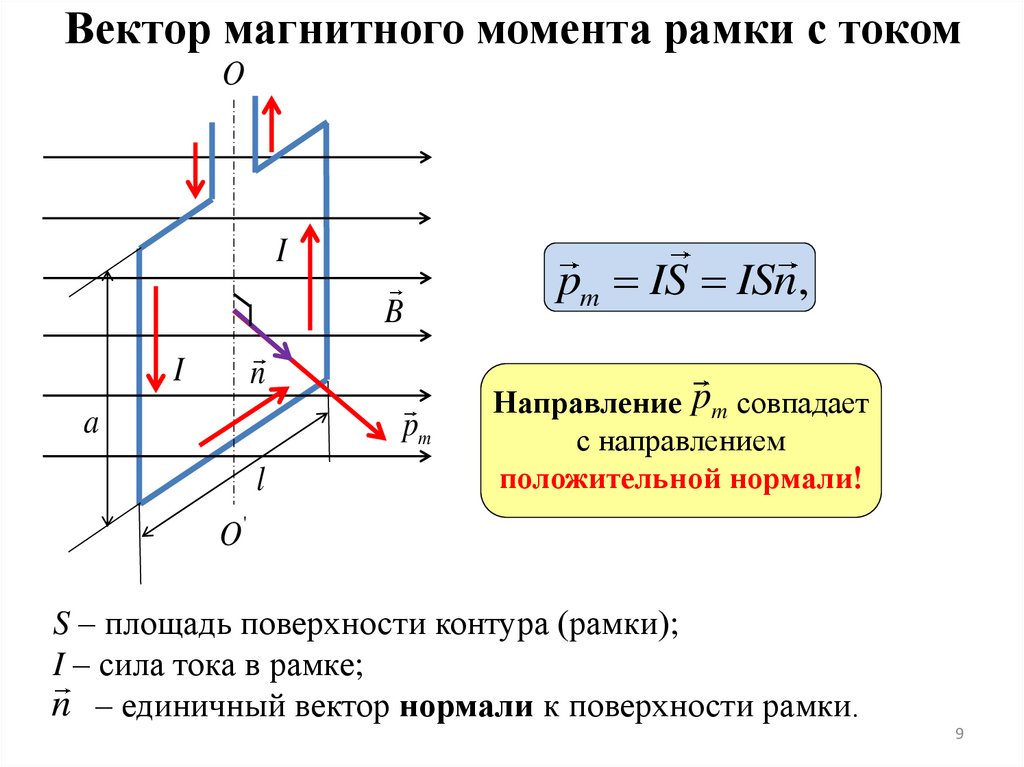
9.

Вектор магнитного момента рамки с током
O
I
B
I
n
a
pm
l
pm IS ISn,
Направление pm совпадает
с направлением
положительной нормали!
O'
S – площадь поверхности контура (рамки);
I – сила тока в рамке;
n – единичный вектор нормали к поверхности рамки.
9

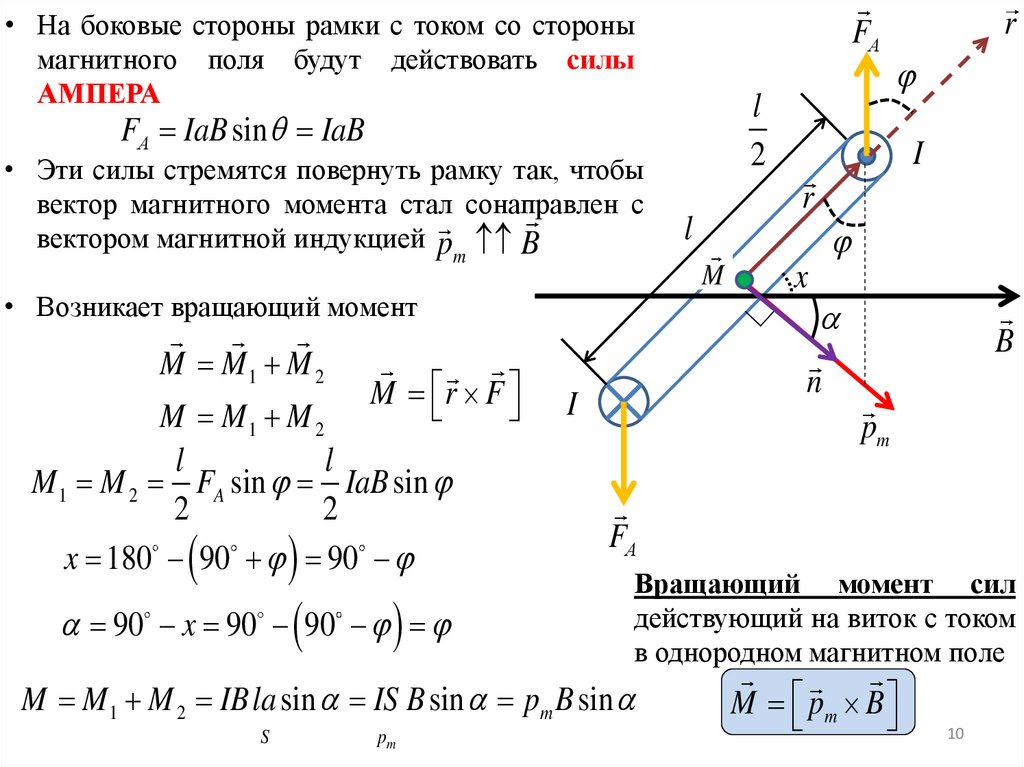
10.

• На боковые стороны рамки с током со стороны
магнитного поля будут действовать силы
АМПЕРА
FА
l
2
FА IaB sin IaB
• Эти силы стремятся повернуть рамку так, чтобы
вектор магнитного момента стал сонаправлен с
вектором магнитной индукцией p B
m
M M1 M 2
M r F
M M1 M 2
l
l
M 1 M 2 FA sin IaB sin
2
2
x 180 90 90
90 x 90 90
pm
I
l
x
B
n
I
pm
FА
Вращающий момент сил
действующий на виток с током
в однородном магнитном поле
M M 1 M 2 IB la sin IS B sin pm B sin
S
r
M
• Возникает вращающий момент
r
M pm B
10

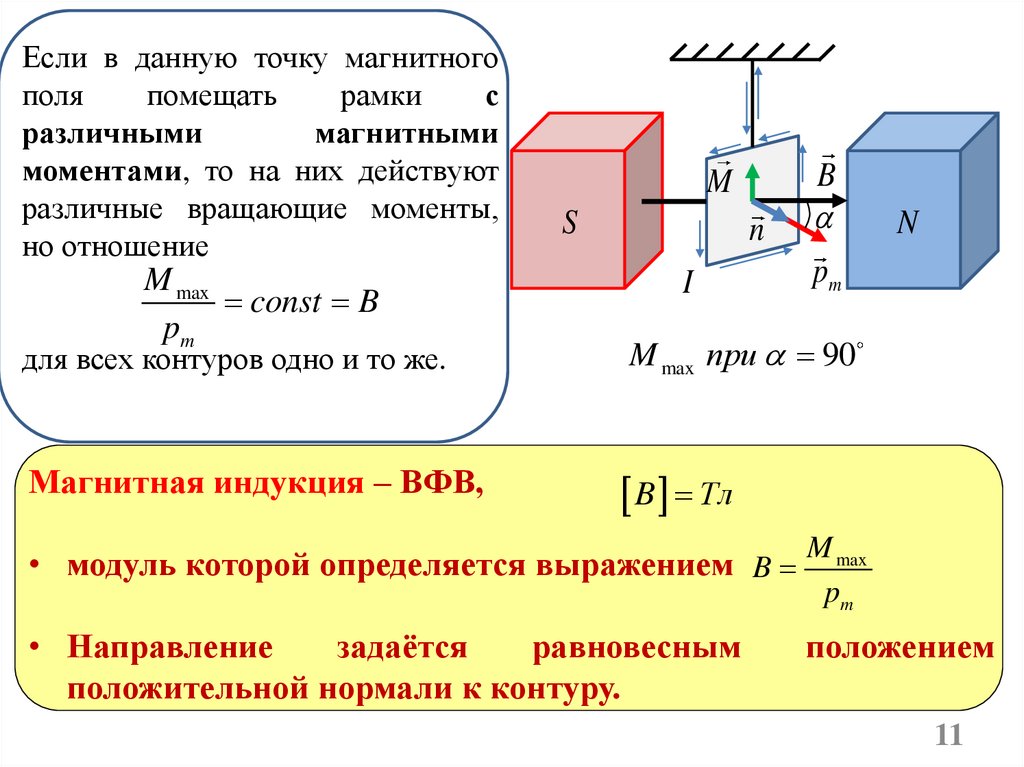
11.

Если в данную точку магнитного
поля
помещать
рамки
с
различными
магнитными
моментами, то на них действуют
различные вращающие моменты,
но отношение
M max
const B
pm
M
S
n
I
B
N
pm
для всех контуров одно и то же.
M max при 90
Магнитная индукция – ВФВ,
B Тл
• модуль которой определяется выражением B
M max
pm
• Направление
задаётся
равновесным
положительной нормали к контуру.
положением
11

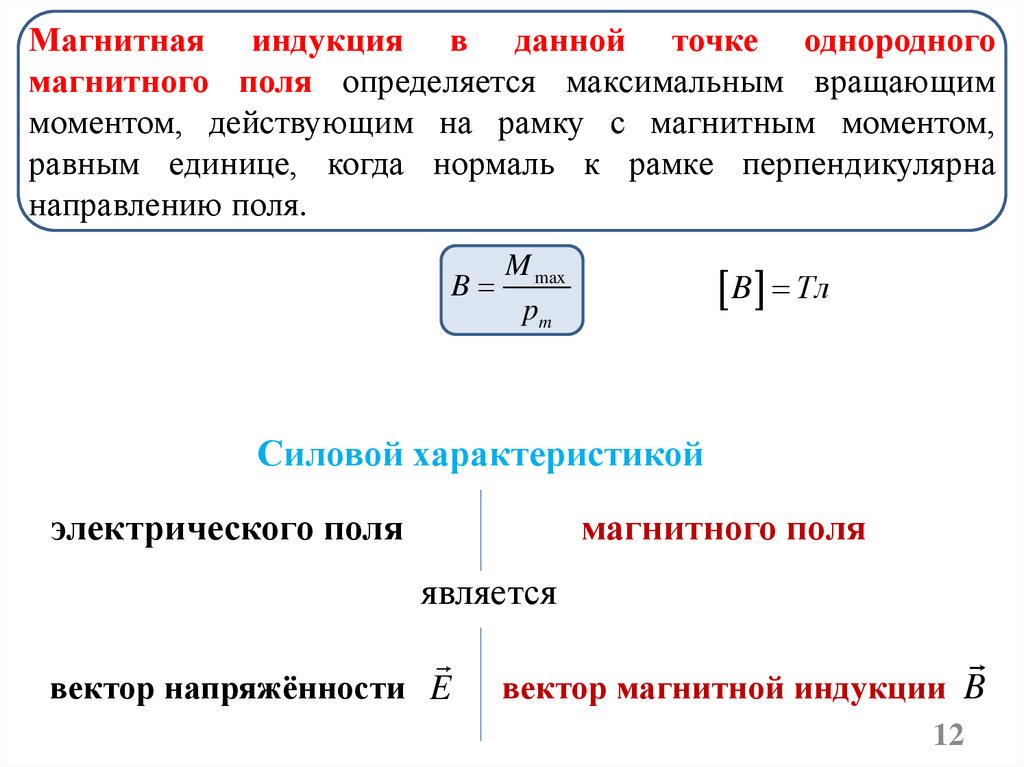
12.

Магнитная индукция в данной точке однородного
магнитного поля определяется максимальным вращающим
моментом, действующим на рамку с магнитным моментом,
равным единице, когда нормаль к рамке перпендикулярна
направлению поля.
M max
B
pm
B Тл
Силовой характеристикой
электрического поля
магнитного поля
является
вектор напряжённости E
вектор магнитной индукции B
12

13.

Силовые линии
электрического поля
магнитного поля
это линии,
касательные к которым
совпадают с направлением
вектора напряжённости E.
Линии напряжённости
всегда разомкнуты
(они начинаются на
положительных и
заканчиваются на
отрицательных зарядах).
касательные к которым в
каждой точке совпадают с
направлением вектора
магнитной индукции B.
Линии магнитной индукции
всегда замкнуты
и охватывают проводники с
током.
13

14.

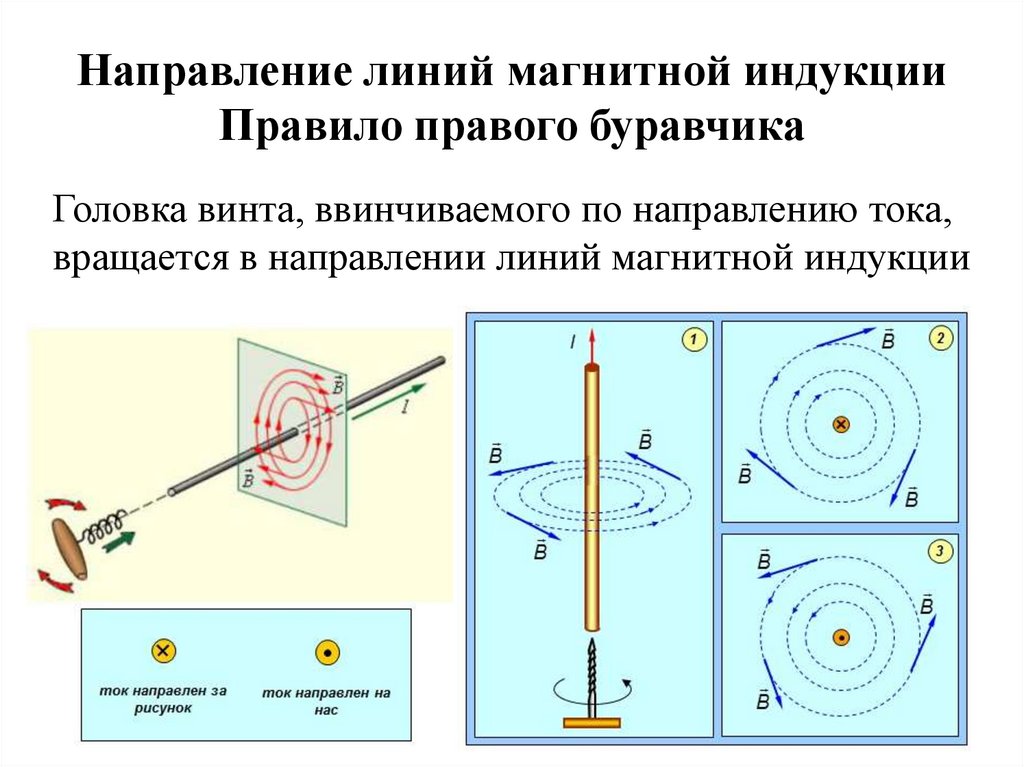
Направление линий магнитной индукции
Правило правого буравчика
Головка винта, ввинчиваемого по направлению тока,
вращается в направлении линий магнитной индукции
14

15.

Магнитное поле
Из опыта известно:
1.
магнитное поле действует на движущиеся заряды
(электрический ток);
2.
движущиеся заряды (электрический ток) создают
магнитное поле.
Электростатическое поле действует как на движущиеся, так и
на неподвижные заряды.
Опыт показывает, что характер воздействия магнитного поля
на ток зависит от:
1) формы проводника, по которому течёт ток;
2) расположения проводника;
3) направления тока.
15

16.

При исследовании
ЭЛЕКТРИЧЕСКОГО ПОЛЯ
МАГНИТНОГО ПОЛЯ
используется
точечный пробный заряд
замкнутый плоский контур
с током
(рамка с током)
16

17.

Принцип суперпозиции магнитных полей
Магнитная
индукция
результирующего
поля,
создаваемого несколькими токами (движущимися
зарядами), равна векторной сумме магнитных индукций
полей, создаваемых каждым током или движущимся
зарядом.
N
B Bi
i 1
Однородное магнитное поле – поле, во всех точках которого
вектор магнитной индукции равен по модулю и направлению.
B const
17

18.

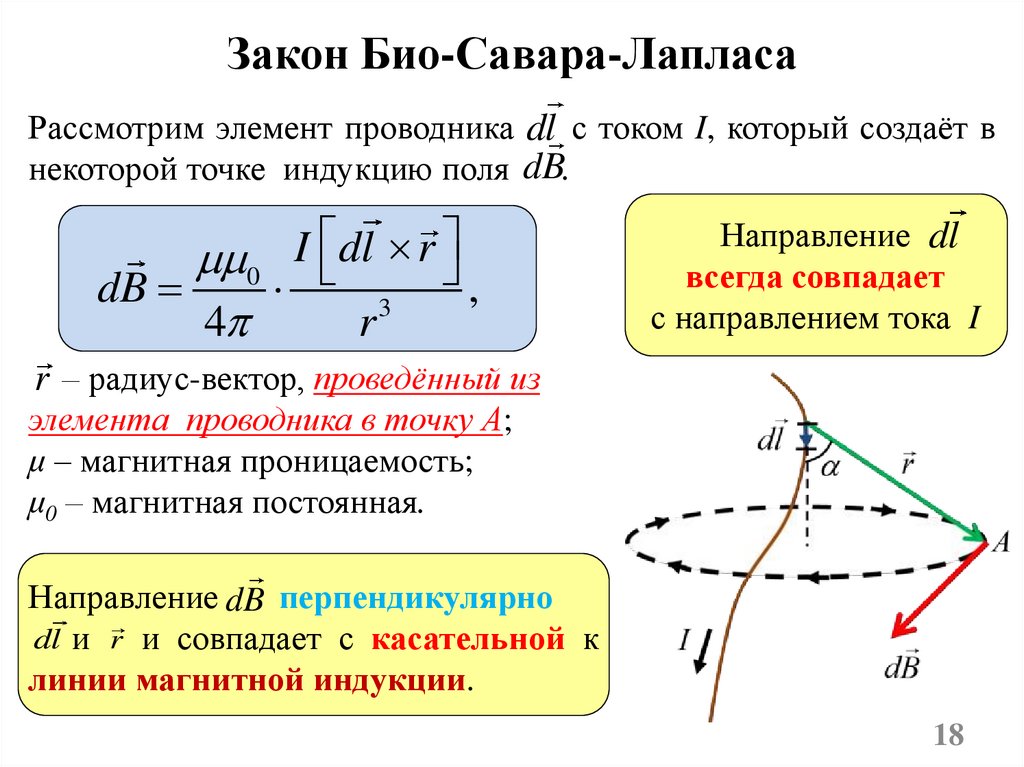
Закон Био-Савара-Лапласа
Рассмотрим элемент проводника dl с током I, который создаёт в
некоторой точке индукцию поля dB.
0 I dl r
dB
,
3
4
r
Направление dl
всегда совпадает
с направлением тока I
r – радиус-вектор, проведённый из
элемента проводника в точку А;
μ – магнитная проницаемость;
μ0 – магнитная постоянная.
Направление dB перпендикулярно
dl и r и совпадает с касательной к
линии магнитной индукции.
18

19.

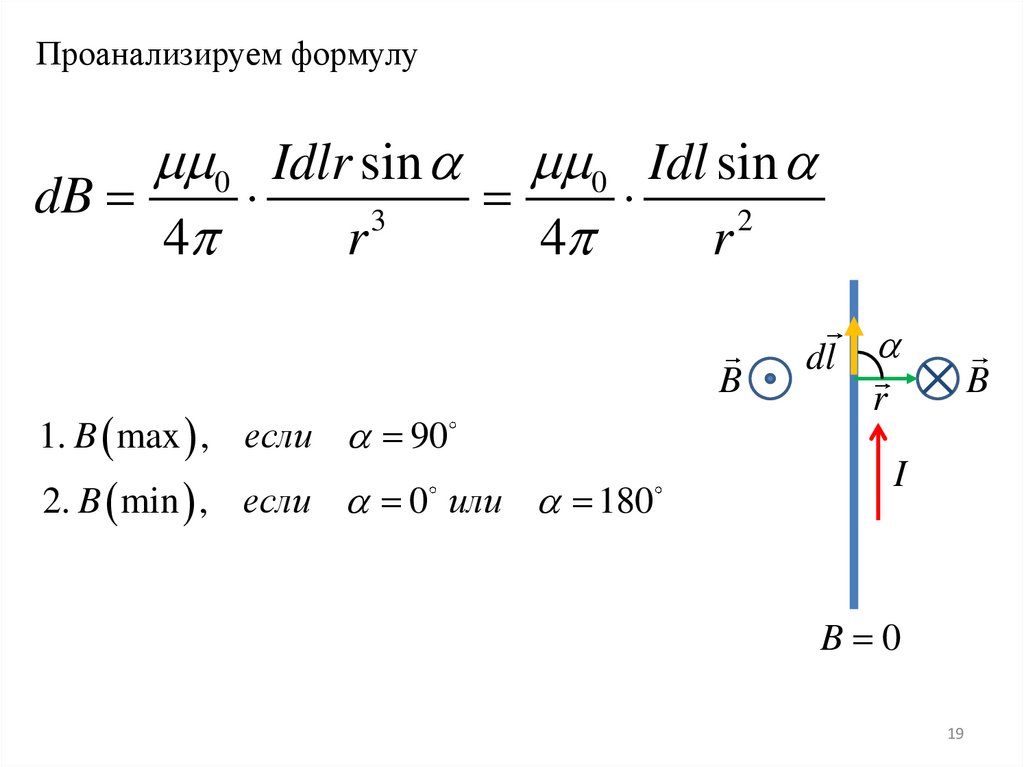
Проанализируем формулу
0 Idlr sin 0 Idl sin
dB
3
2
4
r
4
r
B
1. B max , если 90
2. B min , если 0 или 180
dl
B
r
I
B 0
19

20.

Модуль вектора dB определяется выражением
0 Idlr sin 0 Idl sin
dB
3
2
4
r
4
r
где α – угол между векторами dl и r .
0 4 10
1
7
Гн
;
м
(для вакуума).
Био
Жан Батист
1774 - 1862
Лаплас
Пьер Симон
1749 - 1827
20

21.

Примеры расчёта некоторых магнитных полей
1. Магнитное поле прямого тока
Прямой проводник бесконечной длины
создаёт магнитное поле вокруг себя.
Рассчитаем величину магнитного поля в dl
x
точке А.
Векторы dB от любого элемента длины dl
проводника в точке A имеют одинаковое
направление, перпендикулярное плоскости
чертежа к «нам».
r
d
R
A
I
dB
Исходя из принципа суперпозиции, имеем:
dB dB1 dB2 ... dBn
dB dB1 dB2 ... dBn .
21

22.

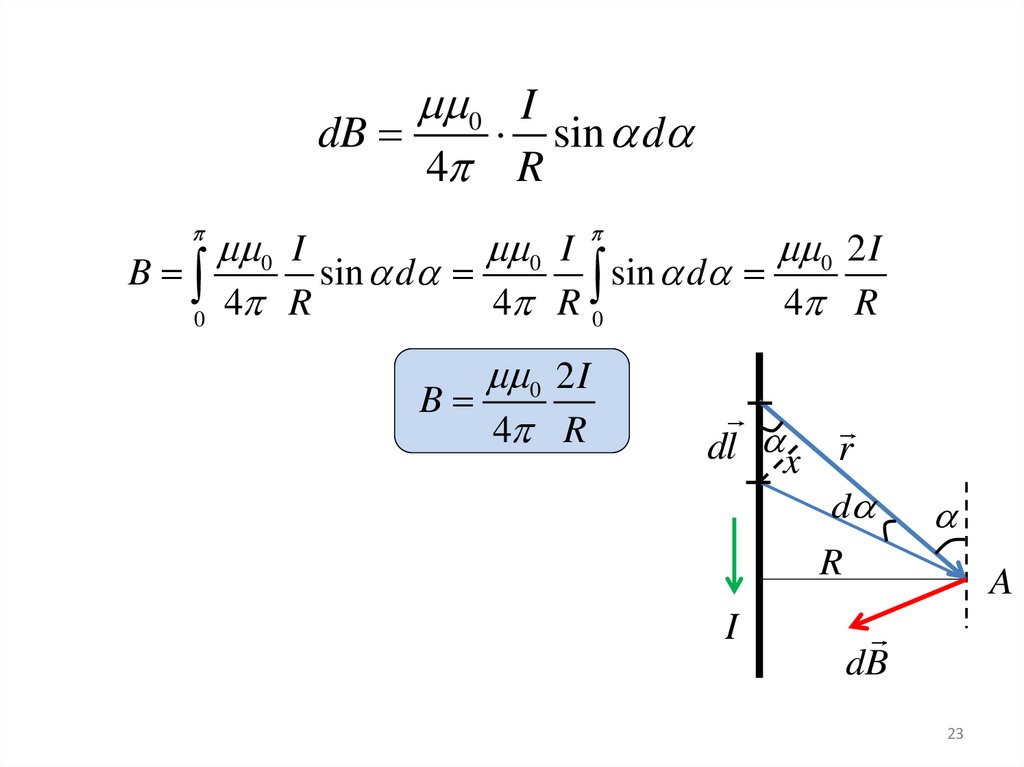
В качестве переменной интегрирования выберем угол α, выразив
через него все остальные величины:
R
rd
r
, dl
.
sin
sin
Подставляем полученные выражения в
формулу Био-Савара-Лапласа,
dl x r
d
R
A
I
dB
0 Idlr sin 0 Idl sin
dB
3
2
4
r
4
r
rd
I
sin
0 sin
0 Id 0 I
sin d
2
4
r
4
r
4 R
22

23.

0 I
dB
sin d
4 R
0 I
0 I
0 2 I
B
sin d
sin d
4 R
4 R 0
4 R
0
0 2 I
B
4 R
dl x r
d
R
A
I
dB
23

24.

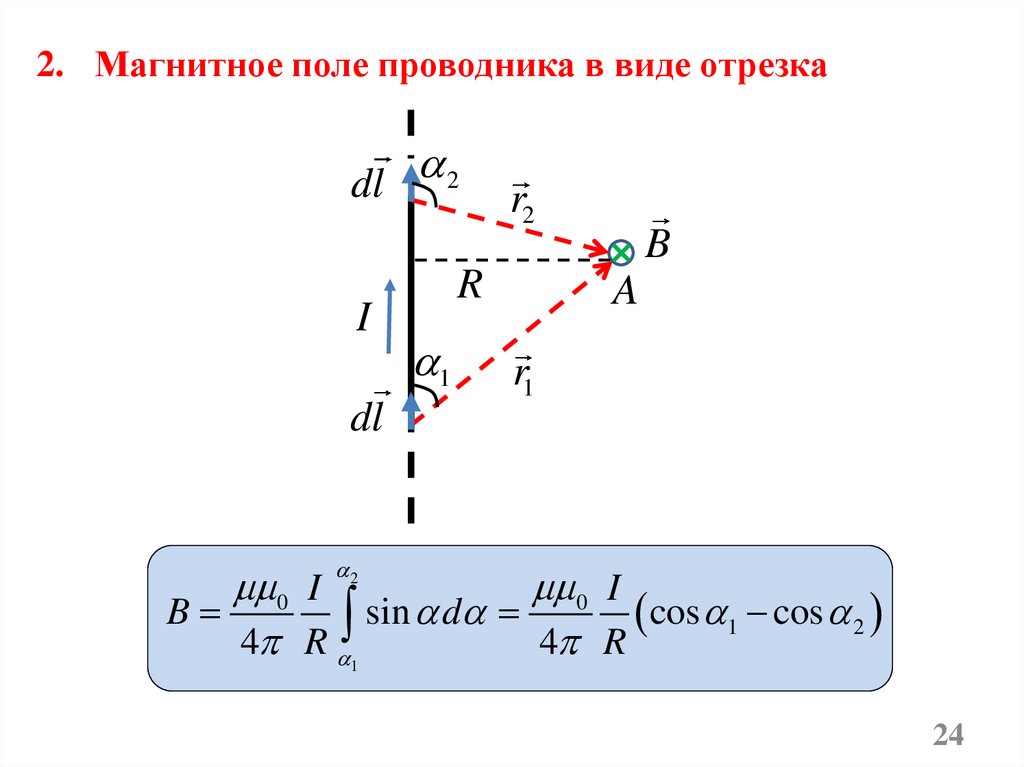
2. Магнитное поле проводника в виде отрезка
dl 2
r2
B
I
R
1
A
r1
dl
2
0 I
0 I
B
sin d
cos 1 cos 2
4 R
4 R
1
24

25.

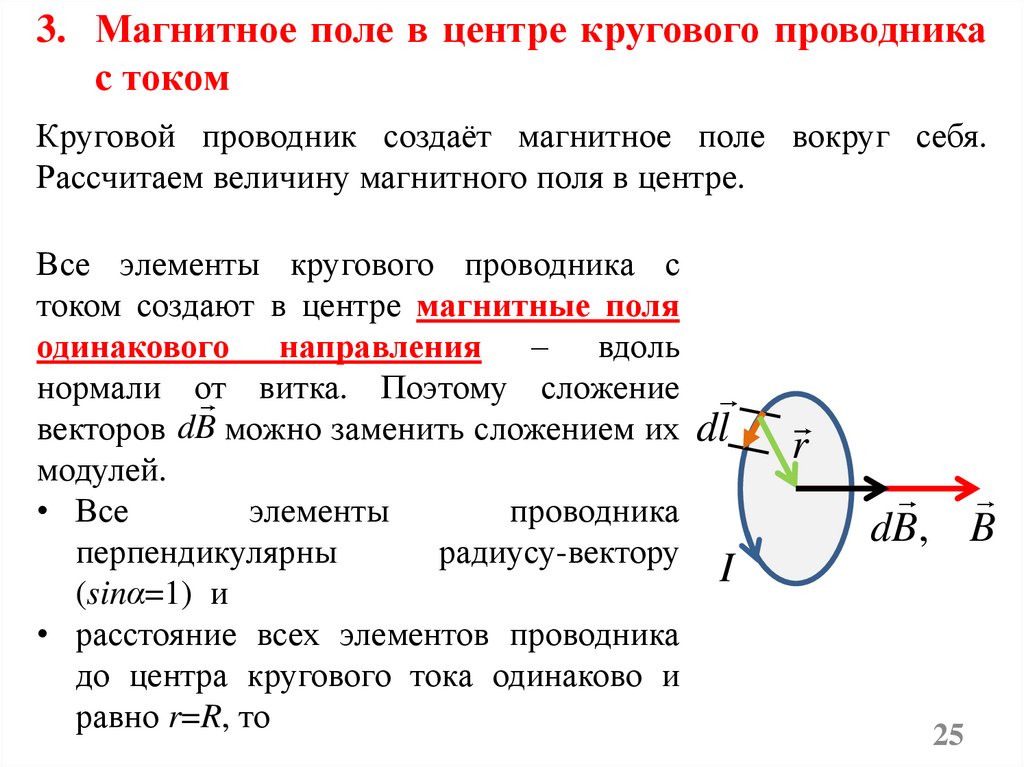
3. Магнитное поле в центре кругового проводника
с током
Круговой проводник создаёт магнитное поле вокруг себя.
Рассчитаем величину магнитного поля в центре.
Все элементы кругового проводника с
током создают в центре магнитные поля
одинакового направления – вдоль
нормали от витка. Поэтому сложение
векторов dB можно заменить сложением их
модулей.
• Все
элементы
проводника
перпендикулярны
радиусу-вектору
(sinα=1) и
• расстояние всех элементов проводника
до центра кругового тока одинаково и
равно r=R, то
dl
r
dB, B
I
25

26.

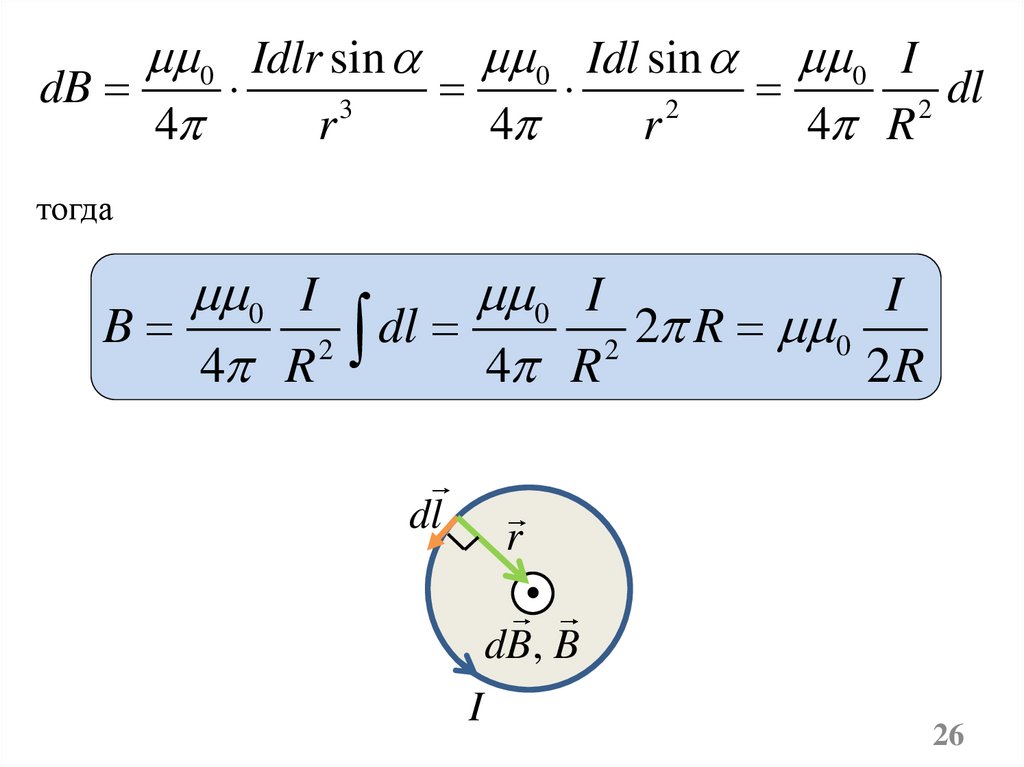
0 Idlr sin 0 Idl sin 0 I
dB
dl
3
2
2
4
r
4
r
4 R
тогда
0 I
0 I
I
B
dl
2 R 0
2
2
4 R
4 R
2R
dl
r
dB, B
I
26

27.

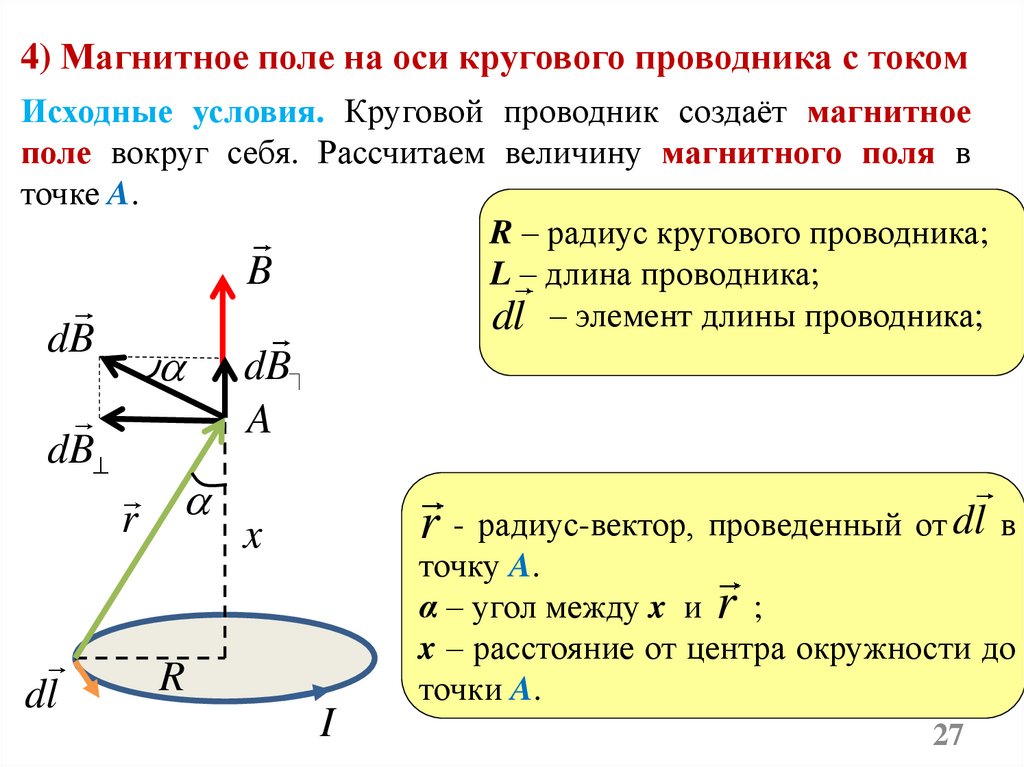
4) Магнитное поле на оси кругового проводника с током
Исходные условия. Круговой проводник создаёт магнитное
поле вокруг себя. Рассчитаем величину магнитного поля в
точке A.
R – радиус кругового проводника;
B
L – длина проводника;
dl – элемент длины проводника;
dB
dB
r
dl
dB
A
r - радиус-вектор, проведенный от dl в
x
R
I
точку A.
α – угол между x и r ;
x – расстояние от центра окружности до
точки A.
27

28.

На расстоянии r от центра витка вдоль оси витка,
магнитное поле будет равно
B dB
L
0
2
IR
R
2
2
x
3
2 2
.
28

29.

Вектор напряжённости
H
магнитного поля
Макроскопические токи – электрические токи,
протекающие по проводникам в электрических цепях.
Магнитное поле макротока описывается
напряжённости магнитного поля H А .
вектором
м
Микроскопические токи
обусловленные движением
молекулах.
–
электрические токи,
электронов в атомах и
Вектор
магнитной
индукции B характеризует
результирующее магнитное поле, создаваемое всеми
макро- и микротоками.
29

30.

Связь между векторами магнитной индукции B
и напряжённостью H магнитного поля
Для однородной изотропной среды вектор магнитной
индукции
B 0 H ,
где μ0 – магнитная постоянная;
μ – магнитная проницаемость среды, безразмерная
величина, показывающая, во сколько раз магнитное поле
макротоков усиливается за счет поля микротоков среды.
30

31.

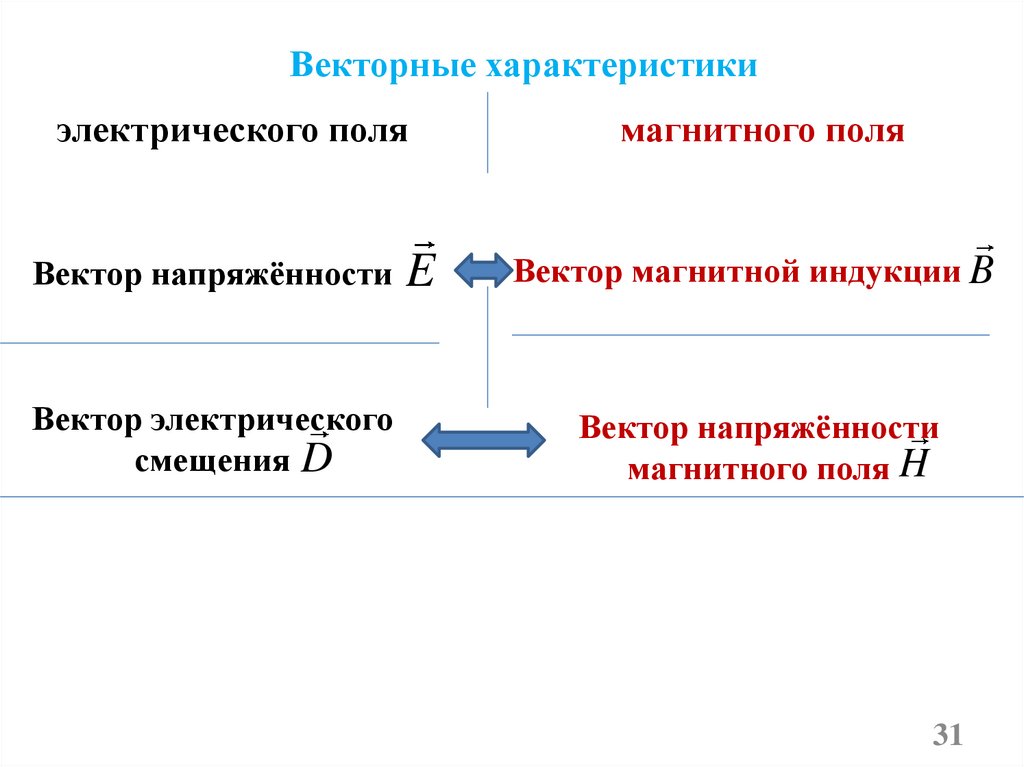
Векторные характеристики
электрического поля
Вектор напряжённости
Вектор электрического
смещения D
E
магнитного поля
Вектор магнитной индукции B
Вектор напряжённости
магнитного поля H
31

32.

Циркуляция вектора магнитной индукции
Циркуляцией вектора B по замкнутому контуру L
называется следующий интеграл по этому контуру:
ЦB
Вdl B cos dl,
L
L
• dl –
элемент
длины
контура,
направленный вдоль обхода контура;
• α – угол между векторами B и dl .
dl
L
32
B

33.

Теорема о циркуляции вектора
магнитной индукции B в вакууме
Циркуляция вектора B по произвольному замкнутому
контуру равна произведению магнитной постоянной μ0 на
алгебраическую сумму токов, охватываемых этим
контуром
ЦB
Вdl
L
n
0 I k
k 1
n – число проводников с токами, охватываемых контуром
произвольной формы.
33

34.

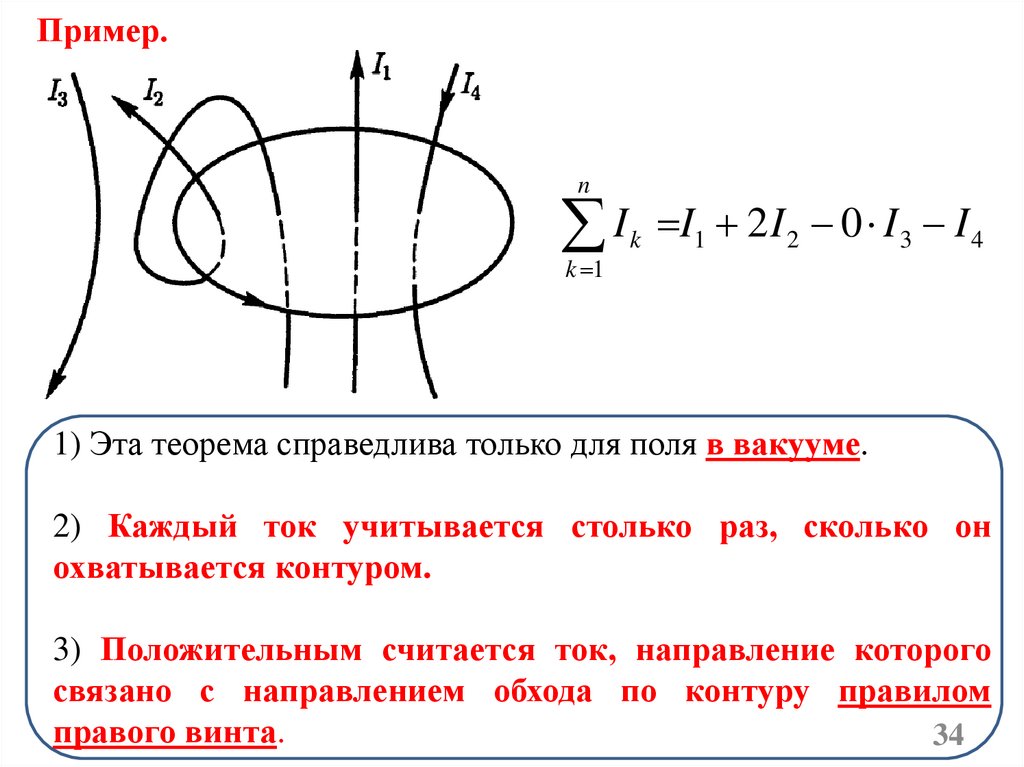
Пример.
n
I
k 1
k
I1 2 I 2 0 I 3 I 4
1) Эта теорема справедлива только для поля в вакууме.
2) Каждый ток учитывается столько раз, сколько он
охватывается контуром.
3) Положительным считается ток, направление которого
связано с направлением обхода по контуру правилом
правого винта.
34

35.

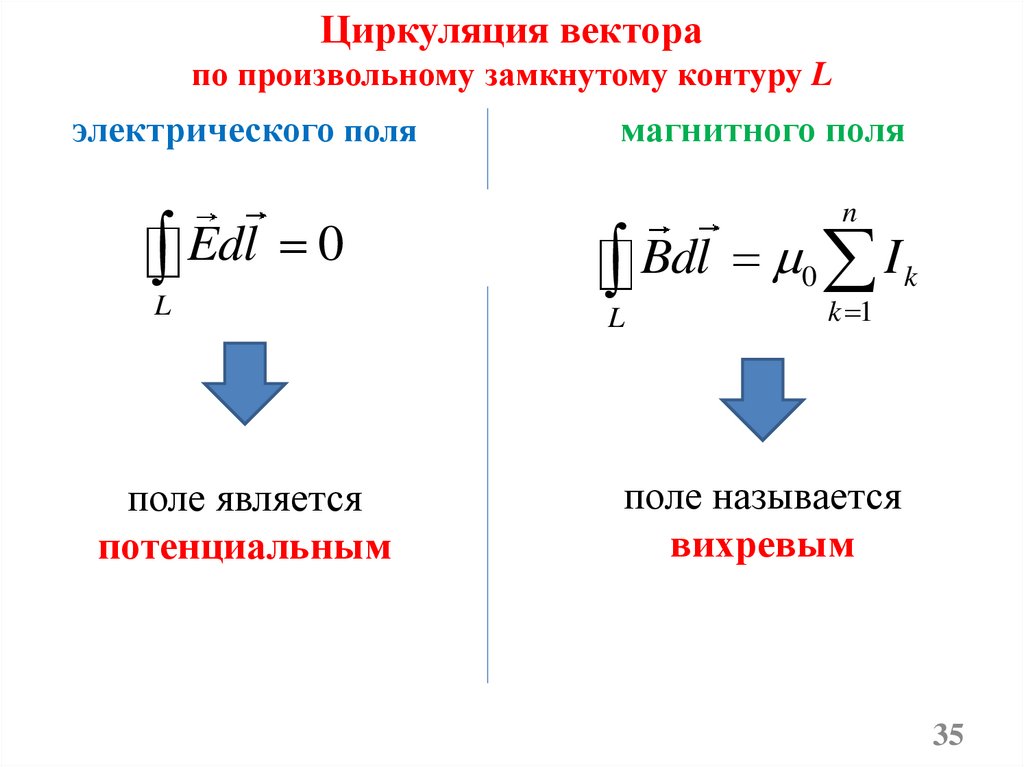
Циркуляция вектора
по произвольному замкнутому контуру L
электрического поля
Edl
0
L
поле является
потенциальным
магнитного поля
n
Bdl I
0
L
k 1
k
поле называется
вихревым
35

36.

Примеры применения
теоремы о циркуляции вектора B
1. Магнитное поле прямого тока
• Замкнутый контур представлен
окружности радиуса r.
B
в
dl
виде
r
I
• В каждой точке этой окружности вектор
магнитной индукции B одинаков по модулю
и направлен по касательной к окружности:
L
Вdl B cos 0 dl B dl B 2 r I
0
L
L
L
0 I
B
2 r
36

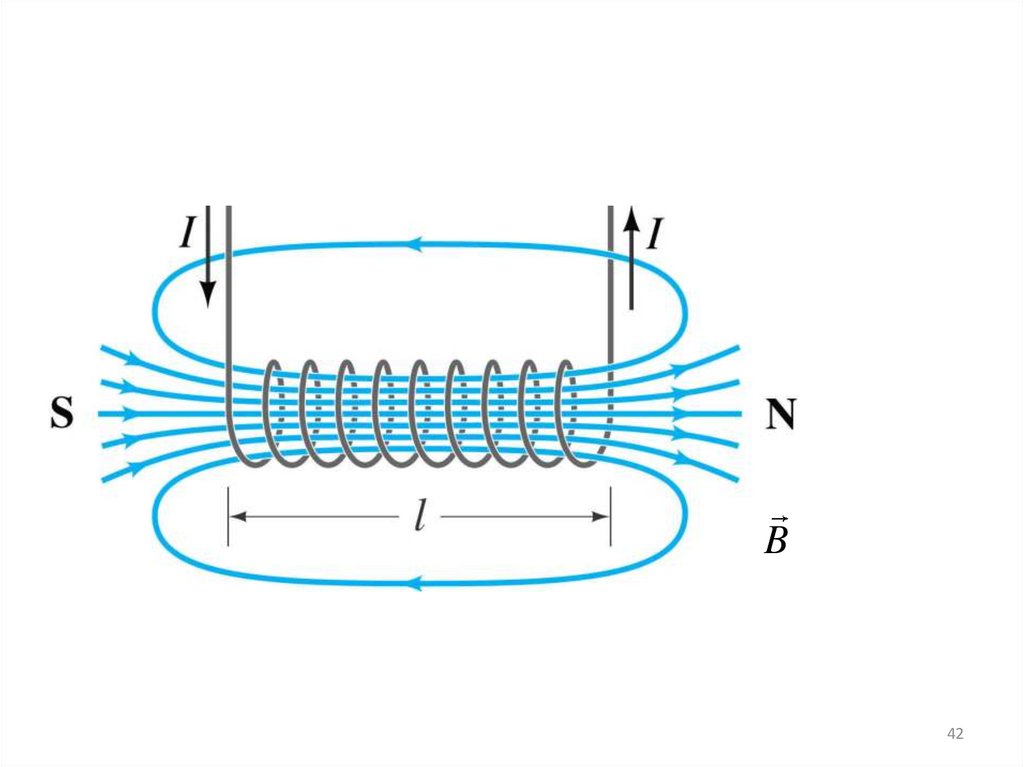
37.

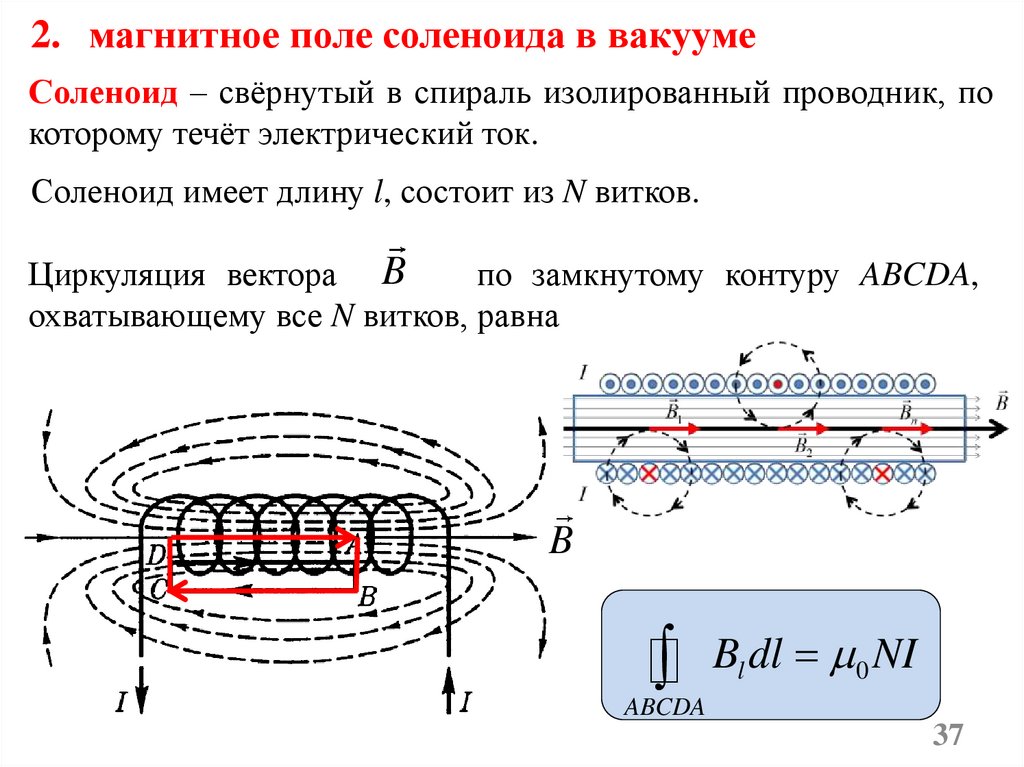
2. магнитное поле соленоида в вакууме
Соленоид – свёрнутый в спираль изолированный проводник, по
которому течёт электрический ток.
Соленоид имеет длину l, состоит из N витков.
Циркуляция вектора B
по замкнутому контуру ABCDA,
охватывающему все N витков, равна
B
Bl dl 0 NI
ABCDA
37

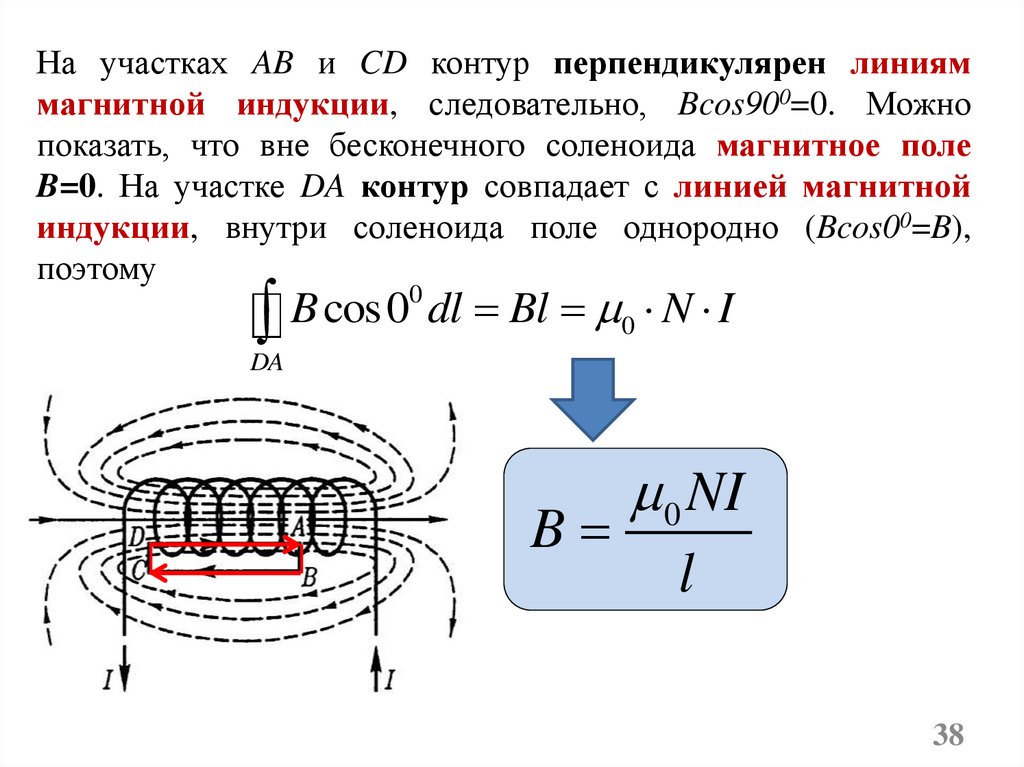
38.

На участках AB и CD контур перпендикулярен линиям
магнитной индукции, следовательно, Bcos900=0. Можно
показать, что вне бесконечного соленоида магнитное поле
B=0. На участке DA контур совпадает с линией магнитной
индукции, внутри соленоида поле однородно (Bcos00=B),
поэтому
B cos 00 dl Bl 0 N I
DA
B
0 NI
l
38

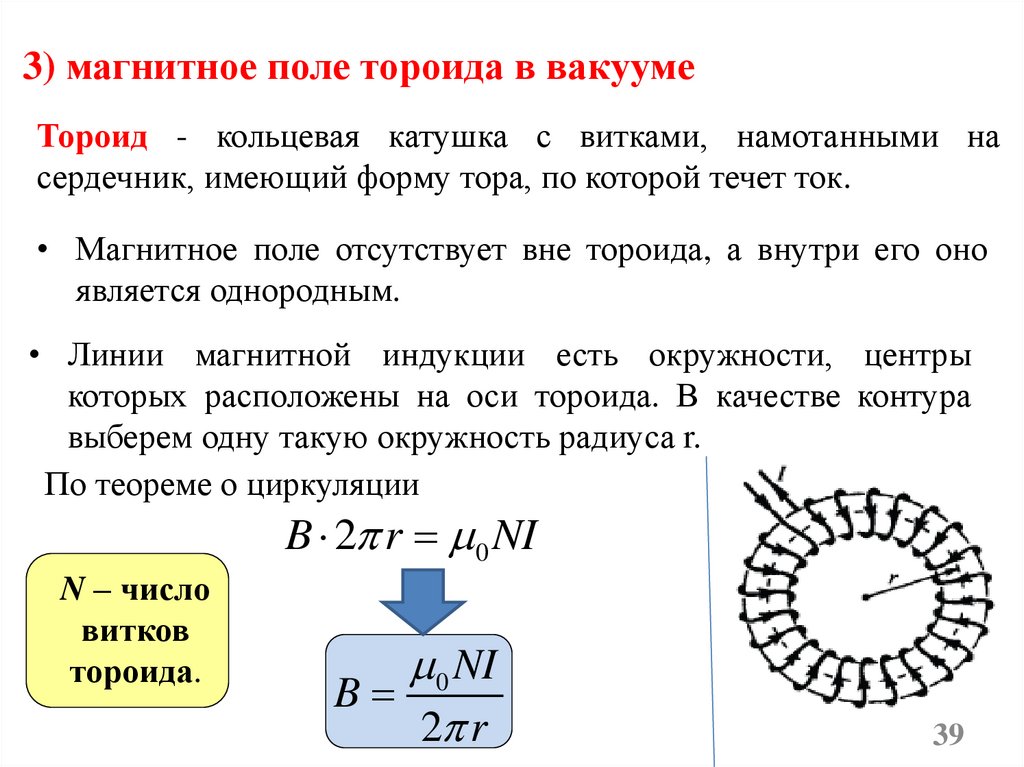
39.

3) магнитное поле тороида в вакууме
Тороид - кольцевая катушка с витками, намотанными на
сердечник, имеющий форму тора, по которой течет ток.
• Магнитное поле отсутствует вне тороида, а внутри его оно
является однородным.
• Линии магнитной индукции есть окружности, центры
которых расположены на оси тороида. В качестве контура
выберем одну такую окружность радиуса r.
По теореме о циркуляции
B 2 r 0 NI
N – число
витков
тороида.
0 NI
B
2 r
39

40.

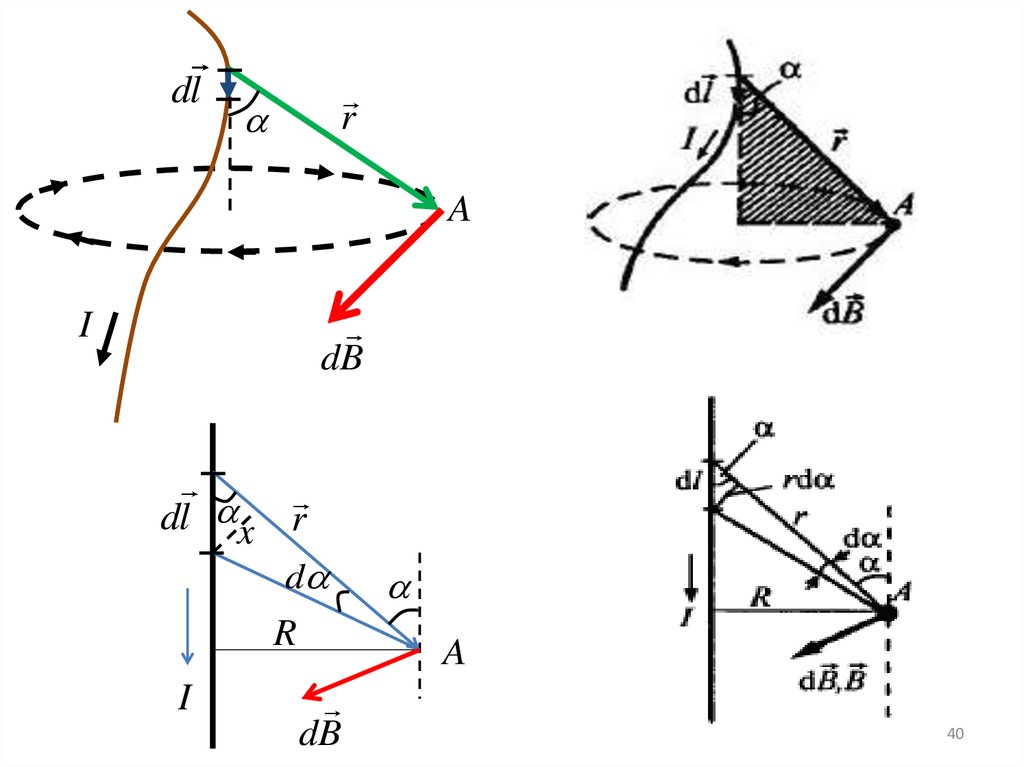
dl
r
A
I
dB
dl x r
d
R
A
I
dB
40

41.

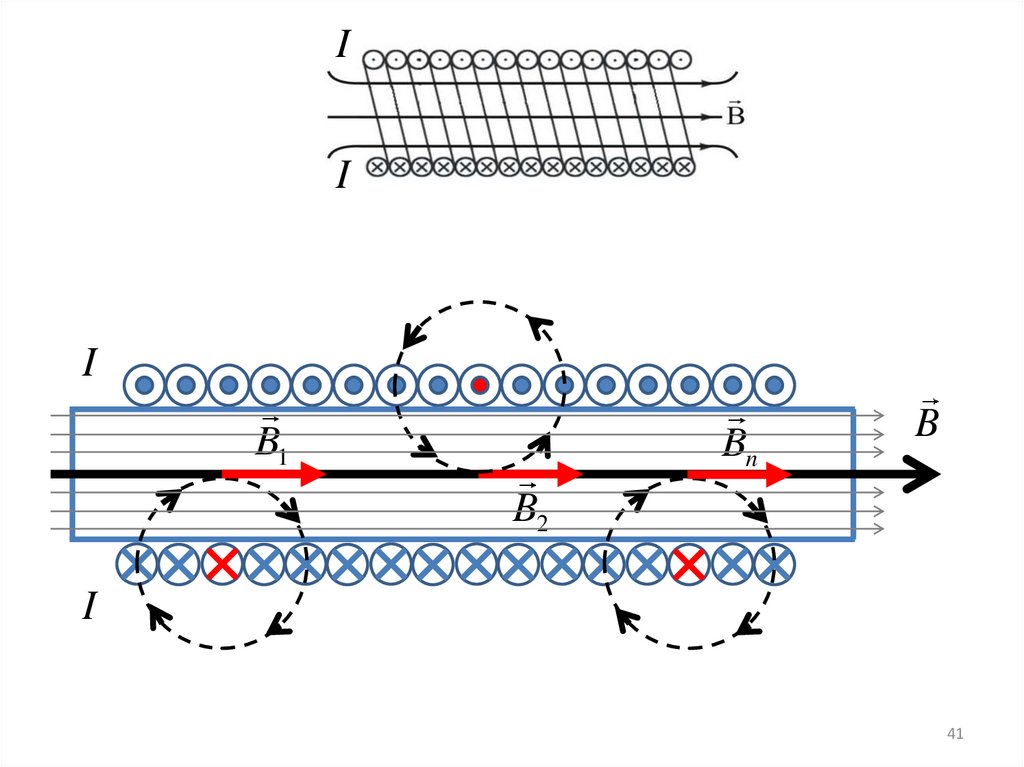
I
I
I
B1
Bn
B
B2
I
41

42.

B
42