Считывание и фильтрация данных с платы TRB3

1. Считывание и фильтрация данных с платы TRB3

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Ф и з и ч е с к и й ф а к ул ьт е т
Гривцова Александра Леонидовна
Считывание и фильтрация данных с
платы TRB3
Новосибирск, 2019 г.

2. Введение

• Настоящая работа посвящена чтению и обработке
данных с электронной платы TRB3, предназначенной для
считывания будущего детектора черенковских колец
Forward RICH на эксперименте PANDA (Германия).
• Плата TRB3 считывает несколько многоанодных
фотоэлектронных умножителей (МаФЭУ) H12700
производства Hamamatsu.
• В работе проводилось моделирование срабатываний от
черенковских фотонов с помощью импульсной лазерной
засветки МаФЭУ и фильтрация срабатываний для
подавления темновых срабатываний с помощью
специально разработанного алгоритма фильтрации.

3. Цель работы

Знакомство с программным обеспечением для сбора и обработки
данных с платы TRB3, с методами обработки экспериментальных
данных. Разработка алгоритма фильтрации для разделения
сигнальных и шумовых срабатываний во временном потоке.
Вид электронной платы TRB3

4. Задачи

• Разработка алгоритмов фильтрации и их испытание на
смоделированных методом Монте-Карло данных.
• Оптимизация параметров алгоритмов и выбор
наилучшего с точки зрения его отношения сигнал/шум.
• Набор экспериментальных данных с ФЭУ и TRB3 при
освещении лазерными импульсами. Сбор данных с
помощью пакета DABC. Обработка данных с помощью
Go4 и собственной программы C++ с использованием
пакета ROOT.
• Применение выбранного фильтра к экспериментальным
данным.

5. Обзор возможных существующих стандартных решений

Для снижения уровня шума существует большое количество фильтров.
В работе были рассмотрены такие фильтры, как фильтр Калмана и фильтр
Винера.

6. Фильтр Калмана

• Фильтр Калмана - это эффективный
рекурсивный фильтр.
• Алгоритм фильтра состоит из двух фаз:
прогноз и коррекция.
• Фаза прогнозирования использует
оценку состояния из предыдущего
такта работы для получения оценки
состояния на текущем этапе. Эта
прогнозируемая оценка состояния
называется априорной оценкой
состояния, поскольку она не включает
в себя информацию наблюдения
текущего шага.
• На этапе коррекции текущая
априорная оценка объединяется с
текущей информацией наблюдения
для уточнения оценки состояния.
Применение фильтра Калмана к показаниям GPS
сенсора

7. Фильтр Винера

• Фильтр Винера является линейным оптимальным фильтром.
• На вход фильтра поступают два сигнала: x[k] и d[k]. При этом d[k]
содержит две составляющие – полезный сигнал s[k], который не
коррелирован с x[k] и шумовую составляющую n[k],
коррелированную с x[k]. Фильтр Винера обеспечивает на выходе
оптимальную в среднеквадратическом смысле оценку y[k]
коррелированной части сигнала (шума) n[k]. Эта оценка
вычитается из d[k] и выход (ошибка) фильтра e[k] – это наилучшая
по среднеквадратическому критерию оценка полезного сигнала.

8. Выбор пути решения

• Подходящие алгоритмы для фильтрации редких сигнальных
событий при наличии шумовой составляющей в литературе не
найдены.
• В работе были разработаны три собственных алгоритма
фильтрации шумов, которые реализованы в Python.
• Для описания принципа работы алгоритмов кратко рассмотрим
соответствующие им функции в программе.

9. Моделирование срабатываний детектора методом Монте-Карло

Моделируется массив срабатываний от сигнальных событий
(коррелированы по времени) и шумовых срабатываний (некоррелированы
по времени)
generate(Nphe, fnoise, sigma_t, stat, fint)
• Nphe – среднее число сигнальных срабатываний на событие
• fnoise – частота шумов (с−1)
• sigma_t – стандартная ошибка времени для сигнальных срабатываний в
событии (нс)
• stat – число сигнальных событий
• fint – частота сигнальных событий (с−1)
Возвращается numpy.ndarray формата [('time','float64'), ('truth','i4’)], где
'time' – время срабатывания детектора,
'truth' – идентификатор срабатывания (<0 – шум; >=0 – номер сигнального
события, к которому относится срабатывание).

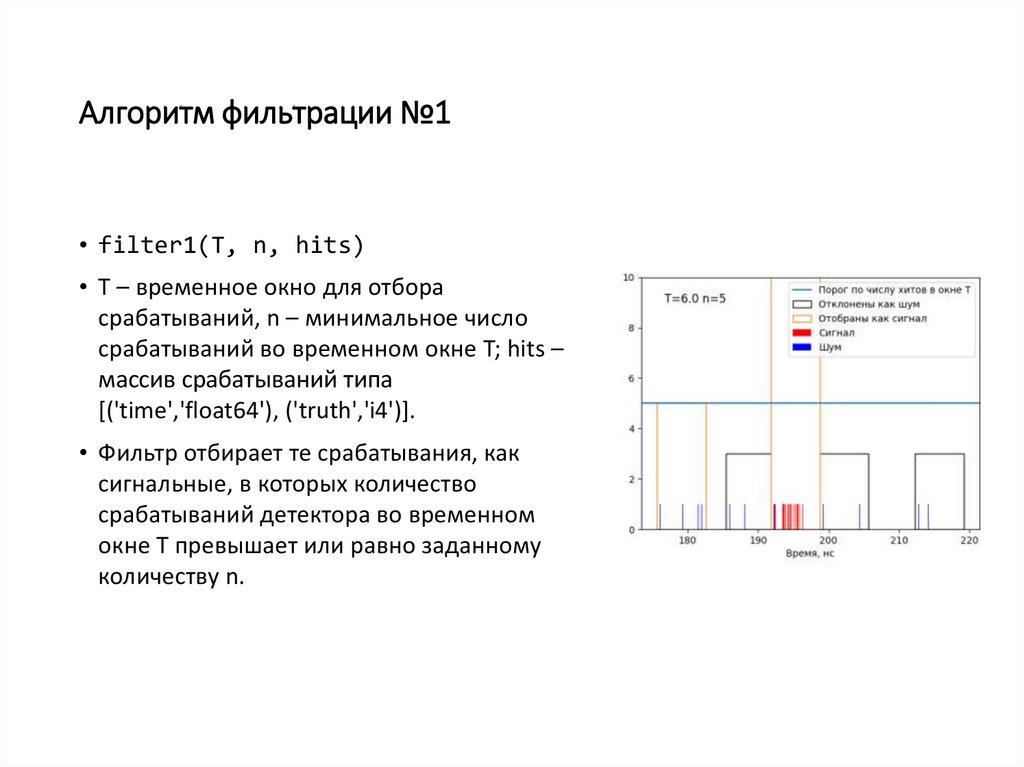
10. Алгоритм фильтрации №1

• filter1(T, n, hits)
• T – временное окно для отбора
срабатываний, n – минимальное число
срабатываний во временном окне T; hits –
массив срабатываний типа
[('time','float64'), ('truth','i4')].
• Фильтр отбирает те срабатывания, как
сигнальные, в которых количество
срабатываний детектора во временном
окне T превышает или равно заданному
количеству n.

11. Алгоритм фильтрации №2

• filter2(p, k, T, hits)
• p – порог по среднему интервалу
между срабатываниями; k – количество
срабатываний; T – временное окно для
отбора сигнальных срабатываний; hits–
массив срабатываний типа
[('time','float64'), ('truth','i4')].
• Фильтр отбирает те срабатывания, как
сигнальные, в которых средний
интервал между первыми k
срабатываниями не превышает
заданный порог p, все остальные
срабатывания в интервале T также
отбираются, как сигнальные.

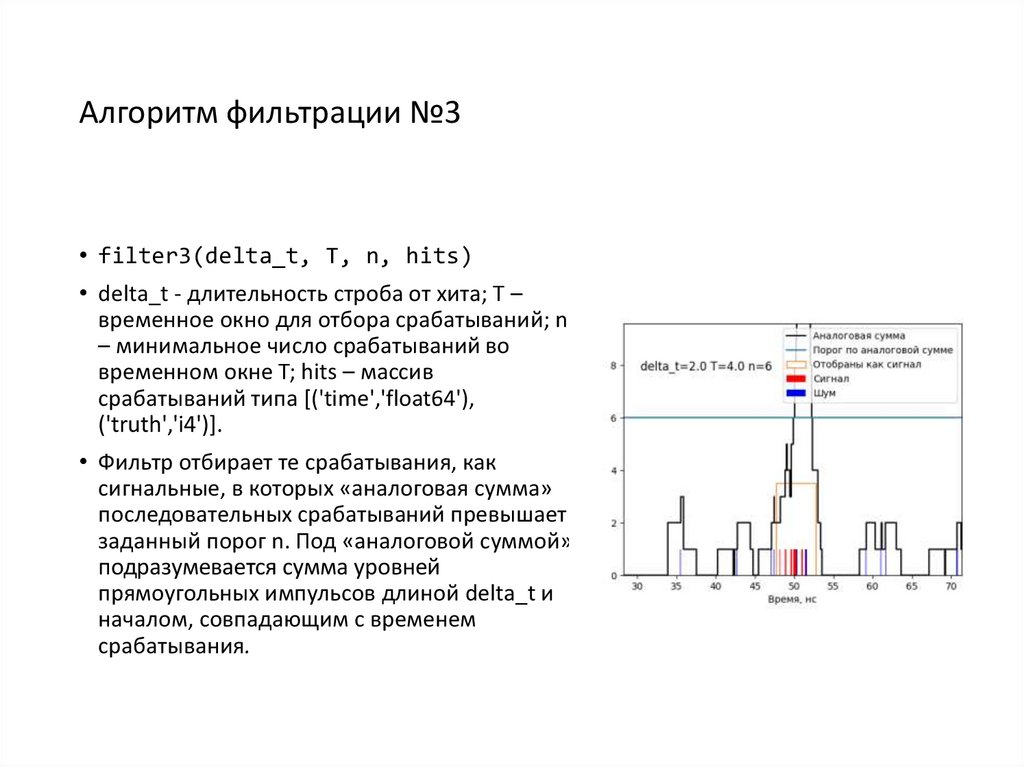
12. Алгоритм фильтрации №3

• filter3(delta_t, T, n, hits)
• delta_t - длительность строба от хита; T –
временное окно для отбора срабатываний; n
– минимальное число срабатываний во
временном окне T; hits – массив
срабатываний типа [('time','float64'),
('truth','i4')].
• Фильтр отбирает те срабатывания, как
сигнальные, в которых «аналоговая сумма»
последовательных срабатываний превышает
заданный порог n. Под «аналоговой суммой»
подразумевается сумма уровней
прямоугольных импульсов длиной delta_t и
началом, совпадающим с временем
срабатывания.

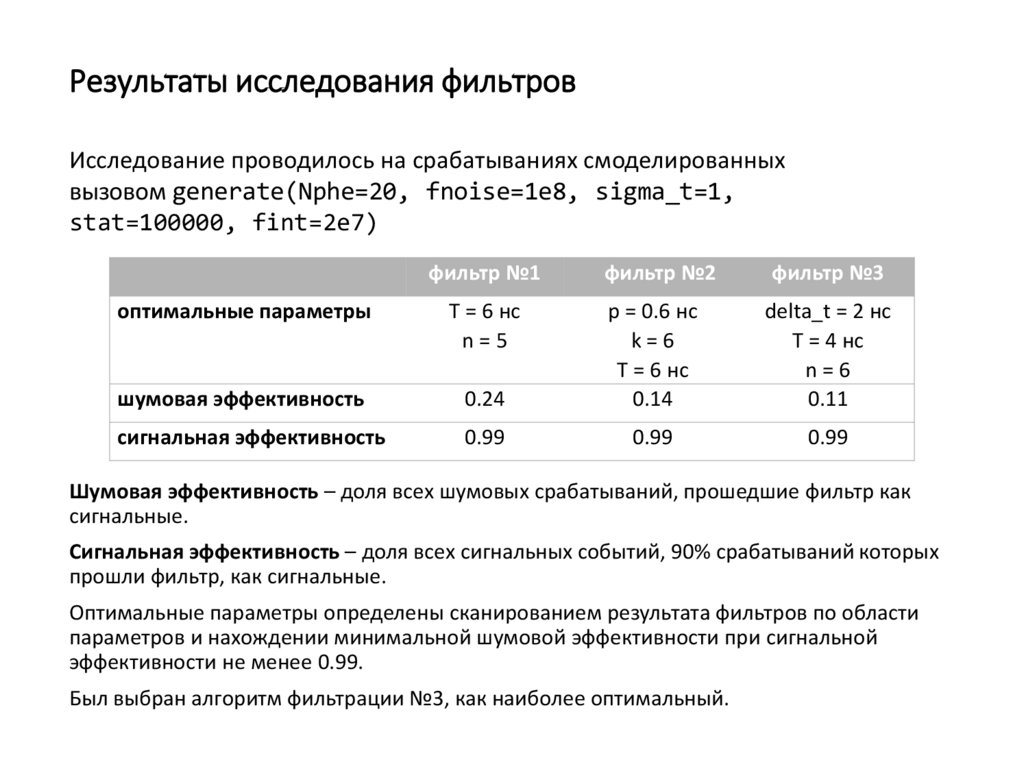
13. Результаты исследования фильтров

Исследование проводилось на срабатываниях смоделированных
вызовом generate(Nphe=20, fnoise=1e8, sigma_t=1,
stat=100000, fint=2e7)
фильтр №1
оптимальные параметры
T = 6 нс
n=5
шумовая эффективность
сигнальная эффективность
фильтр №2
фильтр №3
0.24
p = 0.6 нс
k=6
T = 6 нс
0.14
delta_t = 2 нс
T = 4 нс
n=6
0.11
0.99
0.99
0.99
Шумовая эффективность – доля всех шумовых срабатываний, прошедшие фильтр как
сигнальные.
Сигнальная эффективность – доля всех сигнальных событий, 90% срабатываний которых
прошли фильтр, как сигнальные.
Оптимальные параметры определены сканированием результата фильтров по области
параметров и нахождении минимальной шумовой эффективности при сигнальной
эффективности не менее 0.99.
Был выбран алгоритм фильтрации №3, как наиболее оптимальный.

14. Экспериментальная установка с H12700 и TRB3

Схема экспериментальной установки: 1 – блок-контроллер лазера; 2 –
лазерная головка; 3 – диффузор; 4 – диафрагма; 5 – ФЭУ H12700; 6 – платы
PaDiWa; 7 – платы TRB3; 8 – Ethernet-коммутатор; 9 –компьютер
ФЭУ H12700 (64 канала) засвечивается с помощью лазерных импульсов.
Интенсивность лазера подобрана для одноэлектронных срабатываний в
каналах. Присутствует паразитная постоянная засветка для эмуляции шумов.
Сбор данных с помощью пакета DABC (разработка GSI).
Перекачка данных в ROOT-файл с помощью пакета для анализа данных Go4
(GSI) и собственной программы на C++. Несколько событий сливаются для
эмуляции системы с большим числом каналов и числом фотоэлектронов на
событие 10-20.
Фильтра №3, реализованный на C++, применен к экспериментальным
данным.

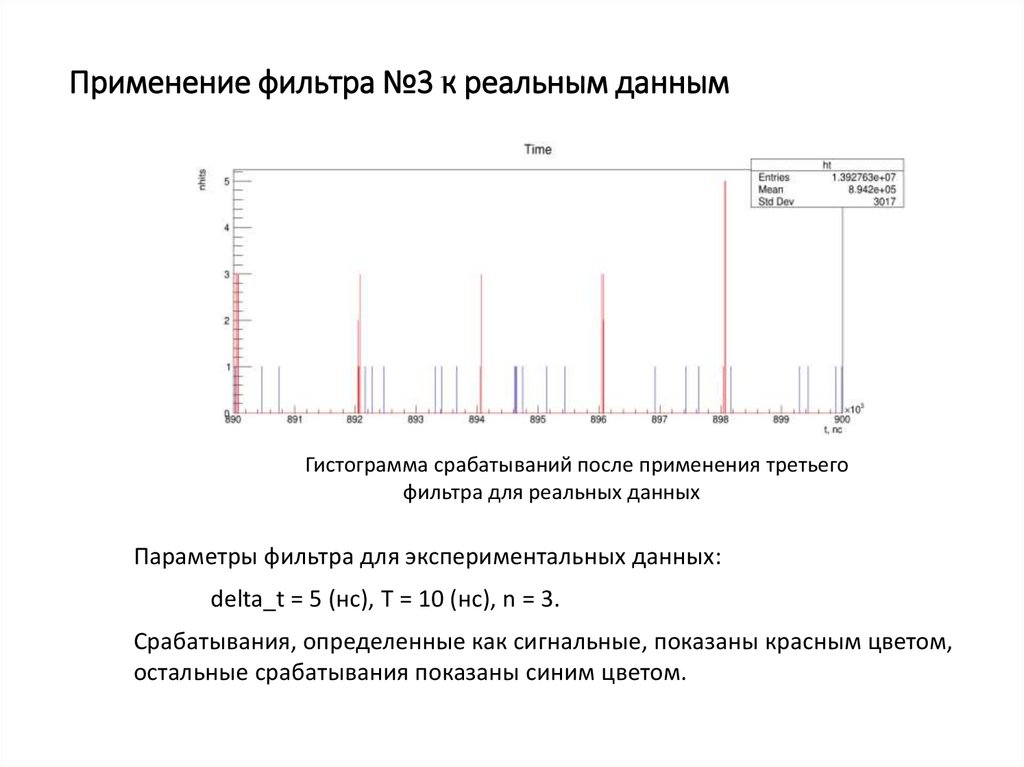
15. Применение фильтра №3 к реальным данным

Гистограмма срабатываний после применения третьего
фильтра для реальных данных
Параметры фильтра для экспериментальных данных:
delta_t = 5 (нс), T = 10 (нс), n = 3.
Срабатывания, определенные как сигнальные, показаны красным цветом,
остальные срабатывания показаны синим цветом.

16. Заключение

• Разработаны 3 алгоритма фильтрации данных по
времени и реализованы на Python. Применены к данным
моделирования методом Монте-Карло.
• Алгоритмы оптимизированы и выбран наилучший с
точки зрения сигнал/шум
• Набраны экспериментальные данные с ФЭУ и TRB3 при
освещении лазерными импульсами. Данные обработаны
с помощью пакета Go4 и собственной программы C++ с
использованием пакета ROOT.
• Выбранный алгоритм фильтрации успешной применен к
экспериментальным данным.

17. Планы

• В настоящей работе был разработан алгоритм для отбора
коррелированных по времени срабатываний и объединения их в
событие, в дальнейшем планируется разработать алгоритм для
отбора коррелированных по времени и координате
срабатываний.
• Планируется реализовать алгоритм на языке VHDL для FPGA