Фильтр Калмана

1. Тема: Фильтр Калмана.

Кафедра Радиоэлектроники.
Преподаватель:
Лазаренко
Сергей Валерьевич.
Радиотехнические цепи и сигналы. Лекция 17.

2.

Учебные вопросы:
1. Формулировка задачи фильтрации.
2.Уравнение фильтра Калмана.
3. Пример построения фильтра
Калмана.
Радиотехнические цепи и сигналы. Лекция 17.

3.

1. Формулировка задачи фильтрации.
При синтезе фильтра Калмана предполагают, что полезный сигнал s(t)
генерируется из белого шума с помощью так называемого формирующего
фильтра в соответствии с алгоритмом
ds t
F t s t G t u t
dt
(1)
Где u(t) - белый шум, спектральная плотность которого равна Q(t) (шум
формирования);
F(t)и G(t) - заданные коэффициенты.
Уравнение (1) называют уравнением формирующего фильтра.
Например, дифференциальное уравнение, описывающее формирующий фильтр,
имеет вид
d 2s
ds
a
a1s b0 u
1
2
dt
dt
Введем обозначения
s s1
(2)
ds
s2
dt
Радиотехнические цепи и сигналы. Лекция 17.

4.

Тогда вместо уравнения (2) можно записать систему
ds1
0 s1 1 s2 0 0
dt
ds2
a0 s1 a1 s2 b0 u
dt
Перепишем эту систему в векторной форме
ds1
d t 0 1 s 0 0 0
1
ds2 a0 a1 s2 0 b0 u
dt
0
Обозначим
1
F
a
a
0 1
ds1
d s d t
,
d t ds2
0 0
dt
G
0
b
0
,
s1
s
s2
0
u
u
Радиотехнические цепи и сигналы. Лекция 17.

5.

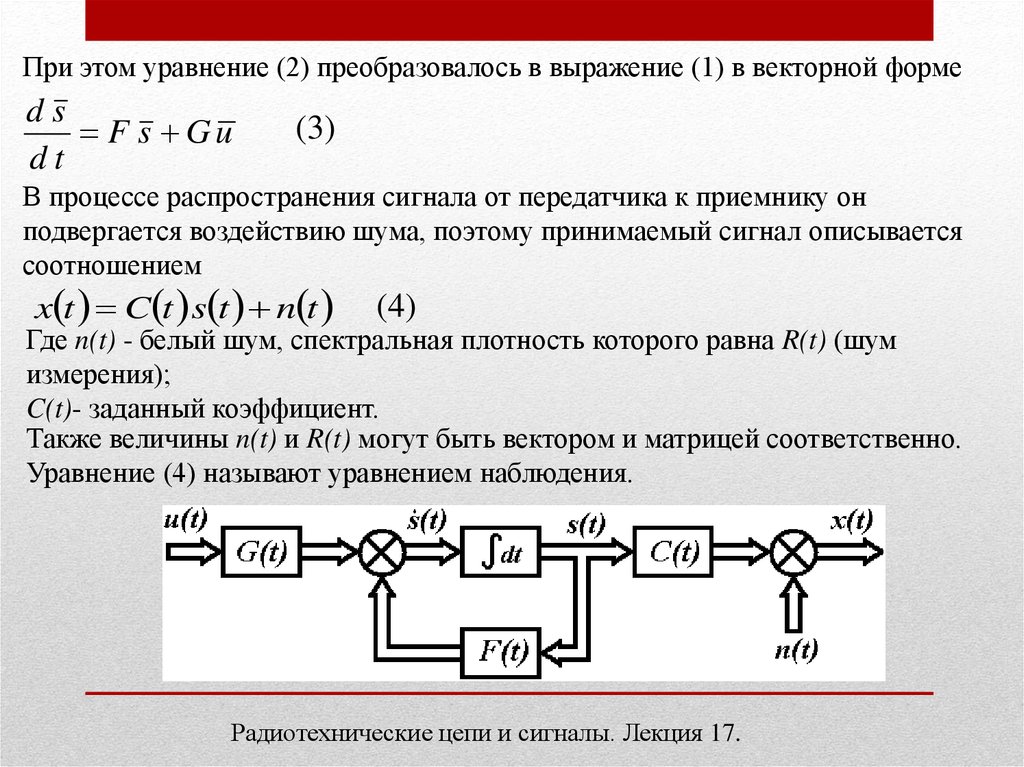
При этом уравнение (2) преобразовалось в выражение (1) в векторной форме
ds
F s Gu
dt
(3)
В процессе распространения сигнала от передатчика к приемнику он
подвергается воздействию шума, поэтому принимаемый сигнал описывается
соотношением
x t C t s t n t
(4)
Где n(t) - белый шум, спектральная плотность которого равна R(t) (шум
измерения);
C(t)- заданный коэффициент.
Также величины n(t) и R(t) могут быть вектором и матрицей соответственно.
Уравнение (4) называют уравнением наблюдения.
Радиотехнические цепи и сигналы. Лекция 17.

6.

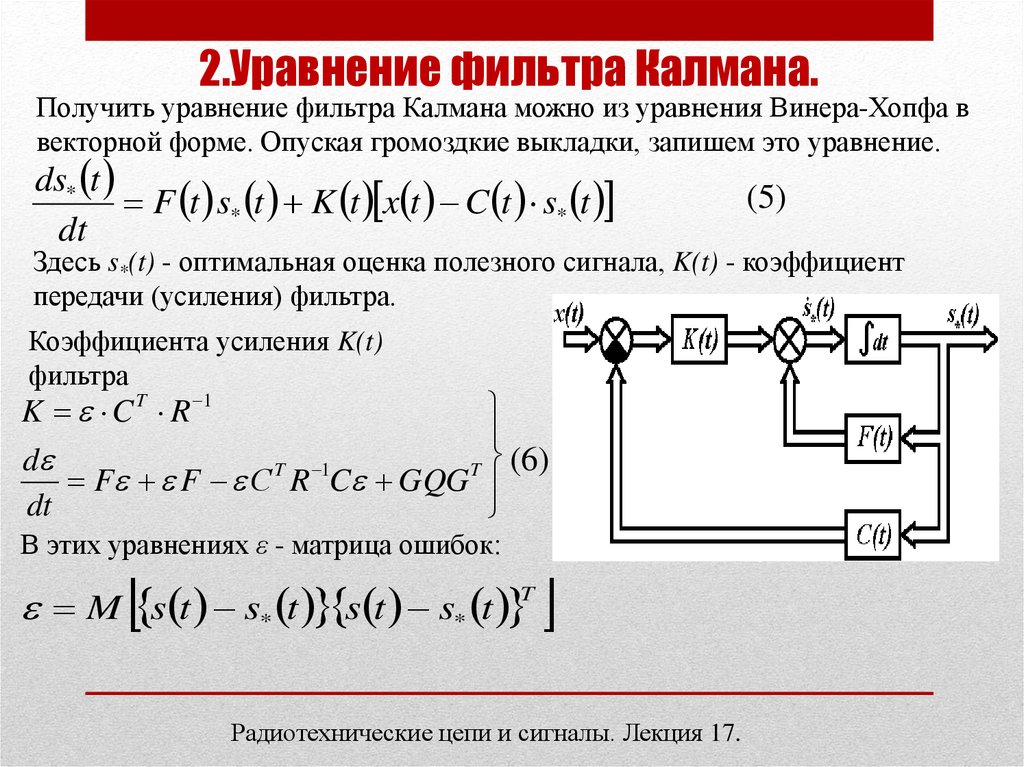
2.Уравнение фильтра Калмана.
Получить уравнение фильтра Калмана можно из уравнения Винера-Хопфа в
векторной форме. Опуская громоздкие выкладки, запишем это уравнение.
ds* t
F t s* t K t x t C t s* t
dt
(5)
Здесь s*(t) - оптимальная оценка полезного сигнала, K(t) - коэффициент
передачи (усиления) фильтра.
Коэффициента усиления K(t)
фильтра
d
T 1
T (6)
F F С R C GQG
dt
K C T R 1
В этих уравнениях ε - матрица ошибок:
M s t s* t s t s* t T
Радиотехнические цепи и сигналы. Лекция 17.

7.

3. Пример построения фильтра Калмана.
На вход фильтра поступает напряжение u(t) в виде
белого шума, спектральная плотность мощности
которого постоянна и равна Q. С учетом этого,
считая выходным сигналом напряжение на
конденсаторе, имеем
ds t 1
1
u t s t
dt
T
T
(7)
где T=CR - постоянная времени цепи.
Сравнивая выражения (7) и (1), делаем вывод, что
F
1
T
1
G
T
Полагая в выражении (4) C=1, запишем уравнение наблюдения
x t s t n t
(8)
где n(t) - белый шум, спектральная плотность мощности которого также
постоянна и равна R.
Радиотехнические цепи и сигналы. Лекция 17.

8.

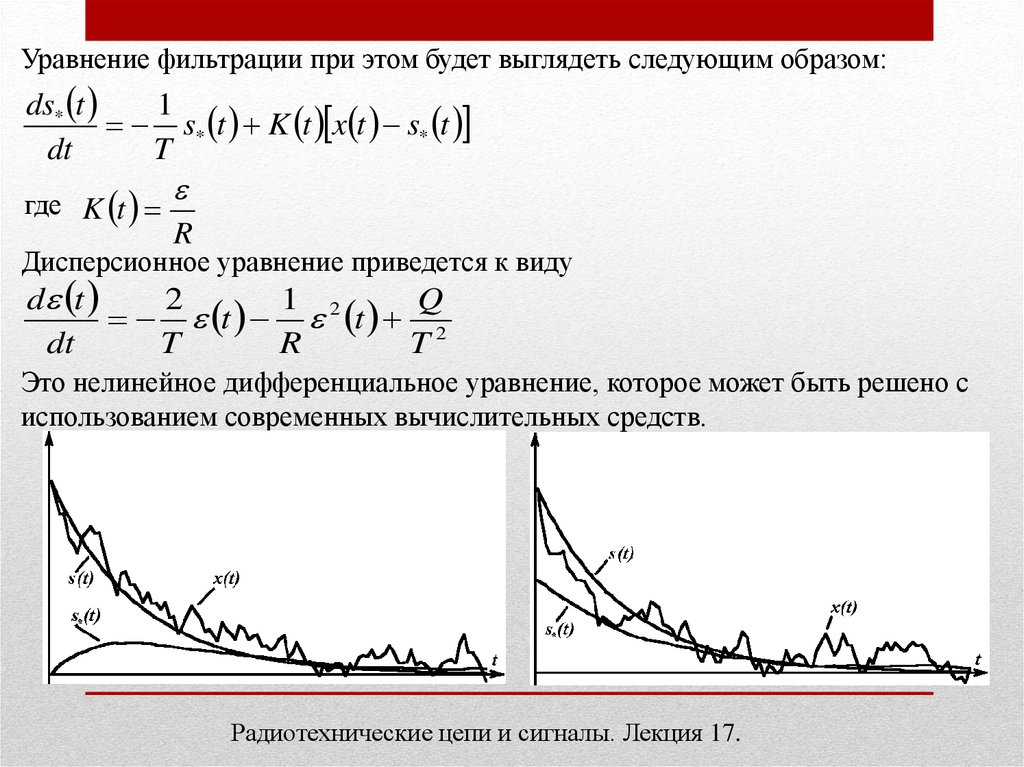
Уравнение фильтрации при этом будет выглядеть следующим образом:
ds* t
1
s* t K t x t s* t
dt
T
где K t
R
Дисперсионное уравнение приведется к виду
d t
2
1
Q
t 2 t 2
dt
T
R
T
Это нелинейное дифференциальное уравнение, которое может быть решено с
использованием современных вычислительных средств.
Радиотехнические цепи и сигналы. Лекция 17.